Classical Model of Rigid Rotor A particle rotating
















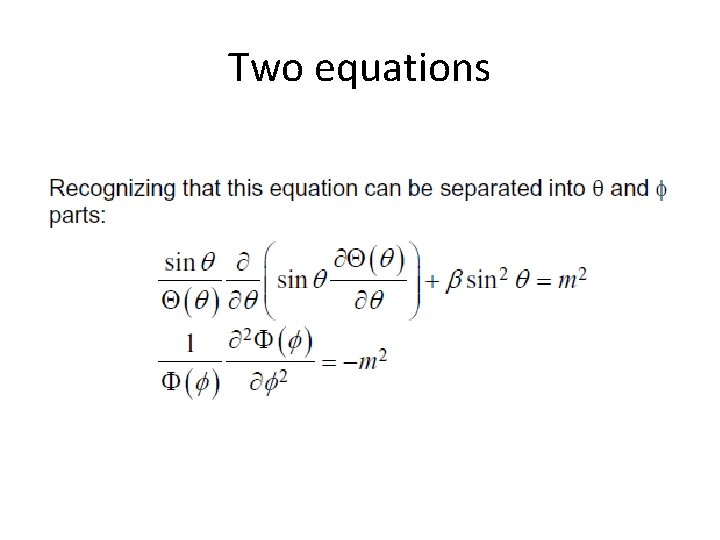

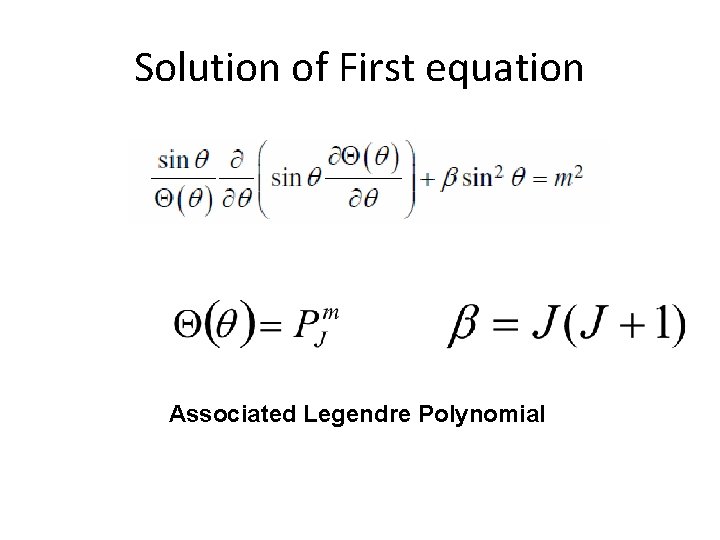



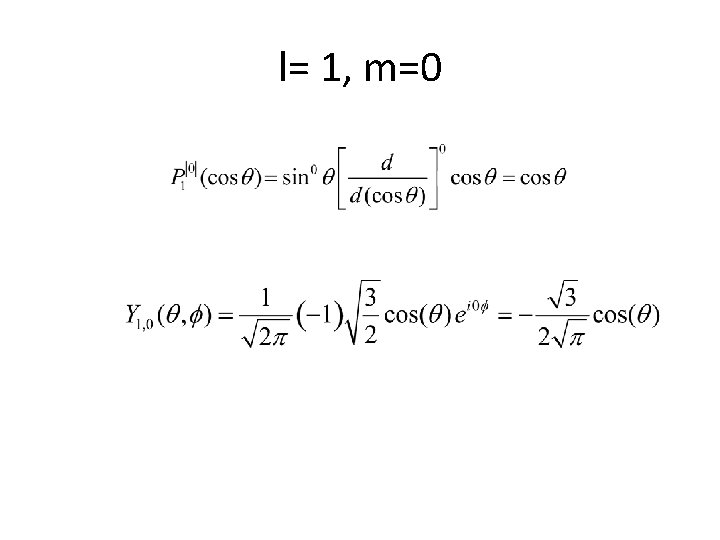








- Slides: 38

Classical Model of Rigid Rotor A particle rotating around a fixed point, as shown below, has angular momentum and rotational kinetic energy (“rigid rotor”) The classical kinetic energy is given by: If the particle is rotating about a fixed point at radius r with a frequency ʋ (s − 1 or Hz), the velocity o the particle is given by: where ω is the angular frequency (rad s− 1 or rad Hz). The rotational kinetic energy can be now expressed as: Also where

Consider a classical rigid rotor corresponding to a diatomic molecule. Here we consider only rotation restricted to a 2 -D plane where the two masses (i. e. , the nuclei) rotate about their center of mass. The rotational kinetic energy for diatomic molecule in terms of angular momentum Note that there is no potential energy involved in free rotation.

Momentum Summary Classical Linear Momentum Energy Rotational Momentum (Angular) Energy QM

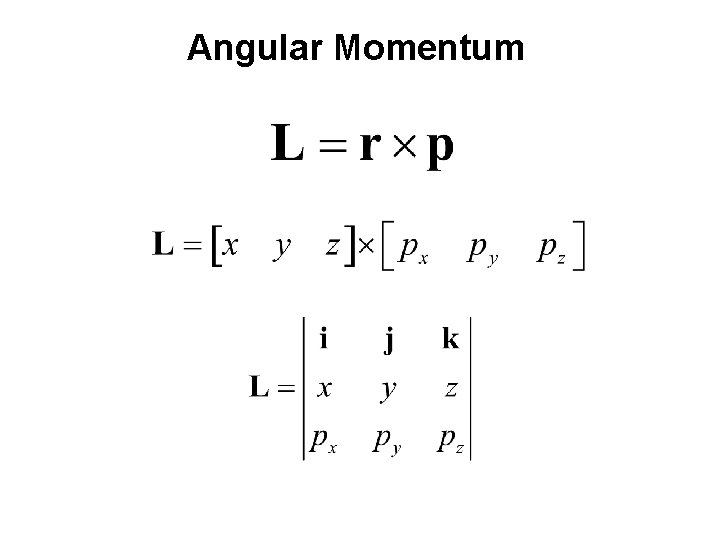
Angular Momentum

Angular Momentum

Angular Momentum

Angular Momentum

Two-Dimensional Rotational Motion Polar Coordinates y r f x

Two-Dimensional Rotational Motion

Two-Dimensional Rigid Rotor Assume r is rigid, ie. it is constant

Two-Dimensional Rigid Rotor

Solution of equation

Energy and Momentum As the system is rotating about the z-axis

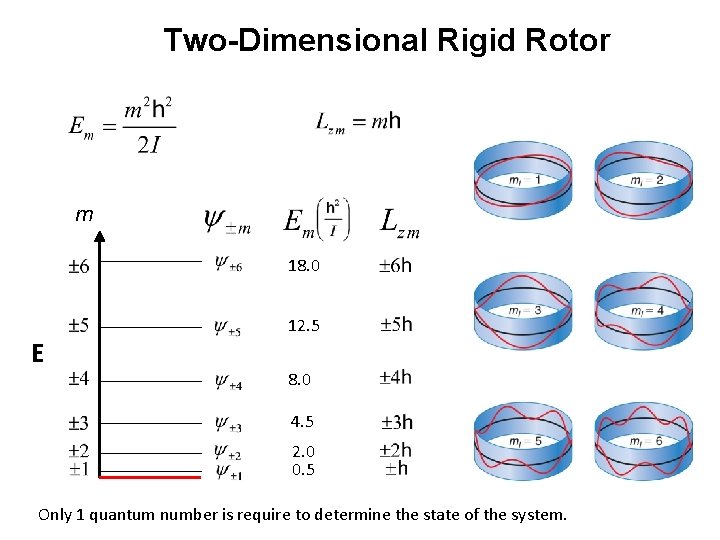
Two-Dimensional Rigid Rotor m 18. 0 12. 5 E 8. 0 4. 5 2. 0 0. 5 Only 1 quantum number is require to determine the state of the system.

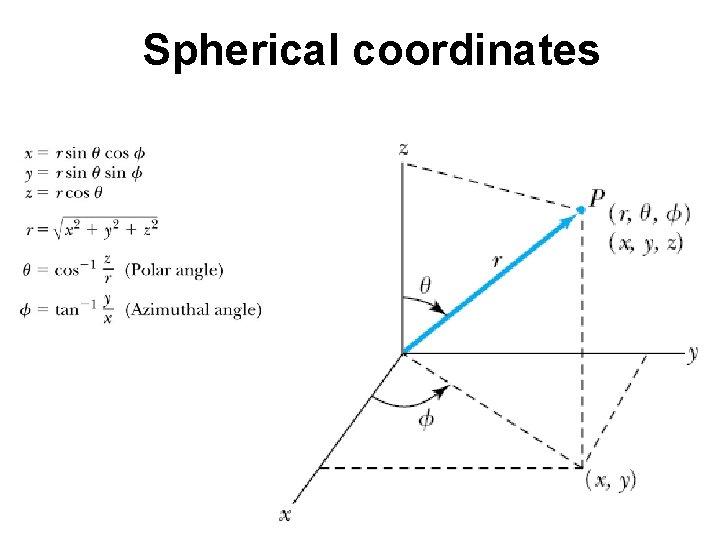
Spherical coordinates

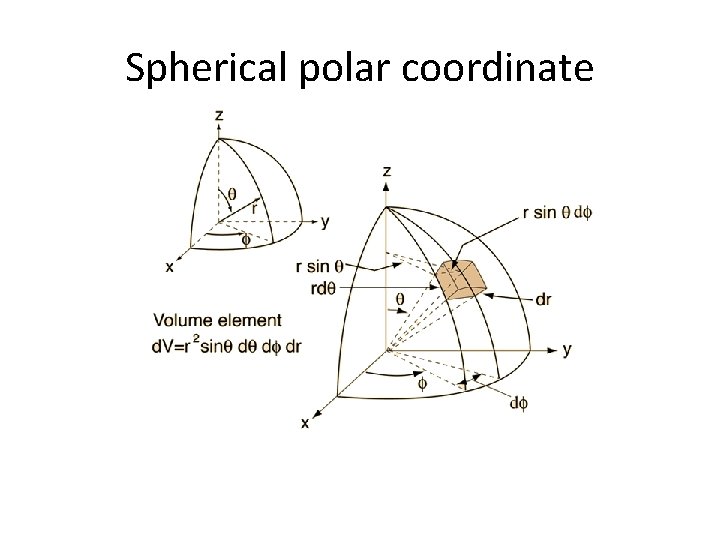
Spherical polar coordinate

Hamiltonian in spherical polar coordinate

Rigid Rotor in Quantum Mechanics Transition from the above classical expression to quantum mechanics can be carried out by replacing the total angular momentum by the corresponding operator: Wave functions must contain both θ and Φ dependence: are called spherical harmonics

Schrondinger equation

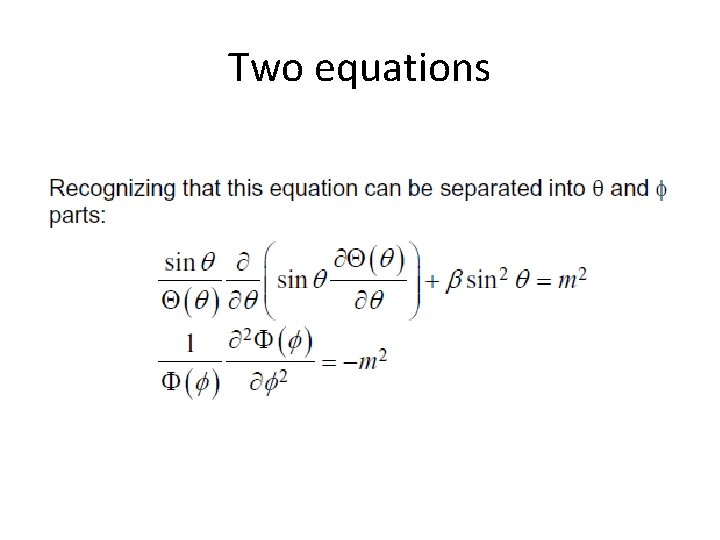
Two equations

Solution of second equation
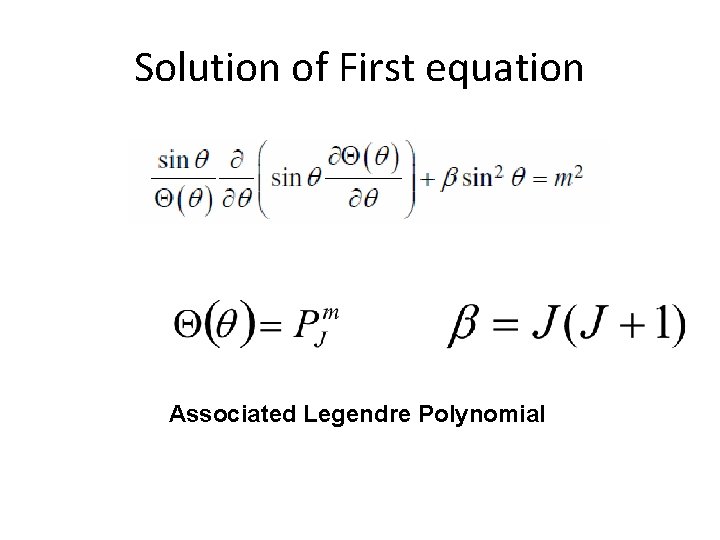
Solution of First equation Associated Legendre Polynomial

Associated Legendre Polynomial

For l=0, m=0

First spherical harmonics Spherical Harmonic, Y 0, 0
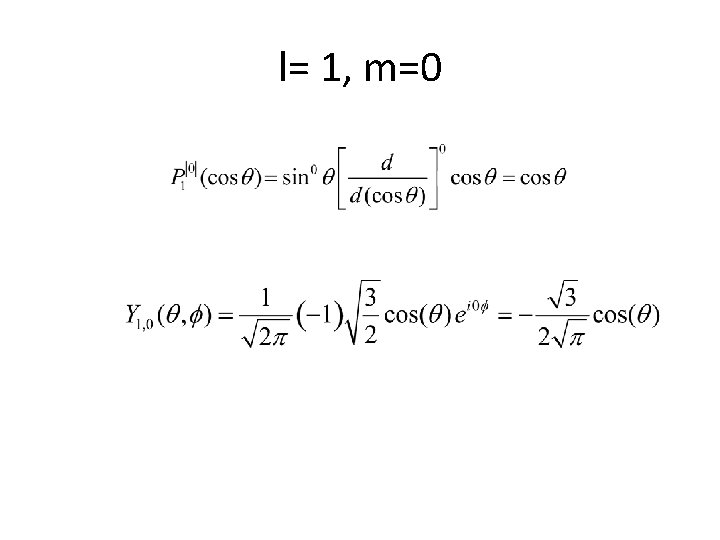
l= 1, m=0

l= 1, m=0 θ cos 2θ 0 1 30 3/4 45 1/2 60 1/4 90 0

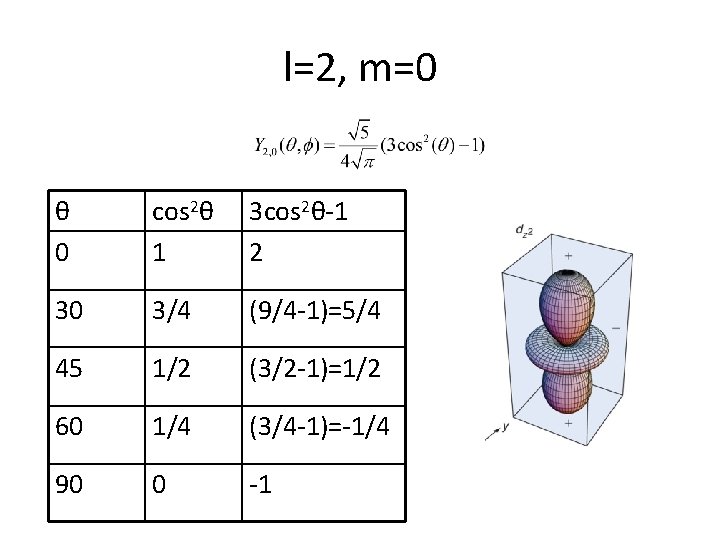
l=2, m=0 θ 0 cos 2θ 1 3 cos 2θ-1 2 30 3/4 (9/4 -1)=5/4 45 1/2 (3/2 -1)=1/2 60 1/4 (3/4 -1)=-1/4 90 0 -1

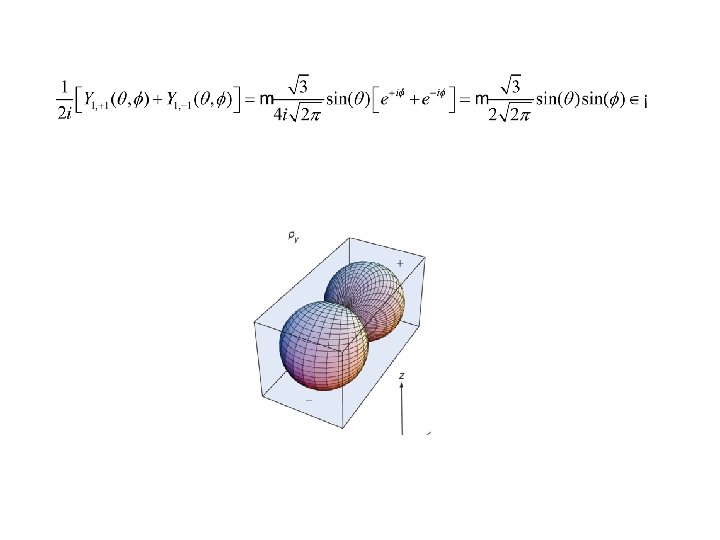
l = 1, m=± 1 Complex Value? ? If Ф 1 and Ф 2 are degenerateeigenfunctions, their linear combinations are also an eigenfunction with the same eigenvalue.

l=1, m=± 1 Along x-axis




E Three-Dimensional Rigid Rotor States l m 32 2 10 -1 -2 -3 6. 0 10 -1 -2 3. 0 1 0 -1 0 1. 0 0. 5 Only 2 quantum numbers are required to determine the state of the system.

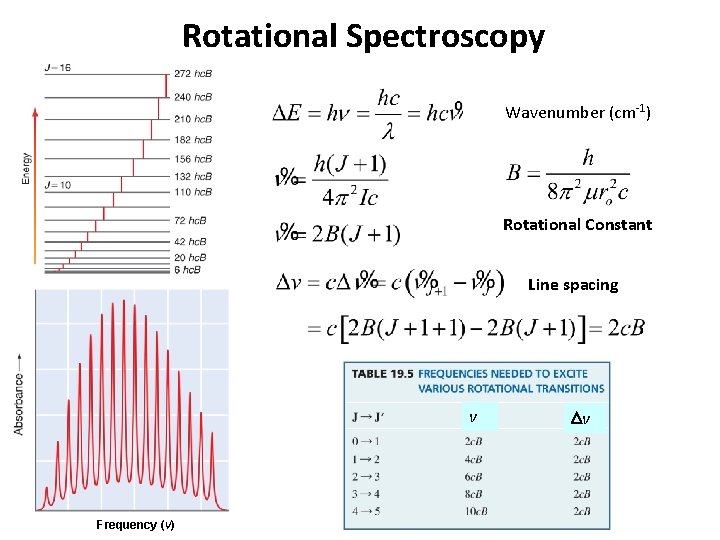
Rotational Spectroscopy J : Rotational quantum number Rotational Constant

Rotational Spectroscopy Wavenumber (cm-1) Rotational Constant Line spacing v Frequency (v) Dv

Bond length • To a good approximation, the microwave spectrum of H 35 Cl consists of a series of equally spaced lines, separated by 6. 26*1011 Hz. Calculate the bond length of H 35 Cl.
 Rigid motion definition
Rigid motion definition 2d rigid rotor
2d rigid rotor Rigid vs non rigid transformations
Rigid vs non rigid transformations Overflow and non overflow dams
Overflow and non overflow dams Irrational function graph
Irrational function graph Rigid body vs particle
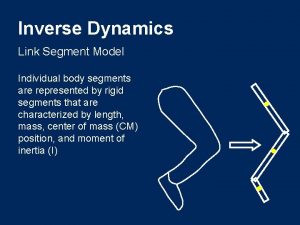
Rigid body vs particle Link-segment model biomechanics
Link-segment model biomechanics Particle model of electricity
Particle model of electricity Particle model of matter exam questions
Particle model of matter exam questions Particle theory evaporation
Particle theory evaporation Wave speed formula
Wave speed formula The particle model describes light as
The particle model describes light as The particle model of light
The particle model of light Dissolving particle theory
Dissolving particle theory Particle model
Particle model Chemistry
Chemistry Types of fermenter
Types of fermenter Rotating nose piece
Rotating nose piece Circulation of air masses
Circulation of air masses Body tube
Body tube Microscope parts
Microscope parts Suzie sees bob rotating clockwise
Suzie sees bob rotating clockwise Rotating conic sections
Rotating conic sections Balancing of several masses rotating in the same plane
Balancing of several masses rotating in the same plane Components of rotary drilling system
Components of rotary drilling system Body of microscope
Body of microscope The analysis of ac circuits uses a rotating vector called a
The analysis of ac circuits uses a rotating vector called a Rotating shaft design
Rotating shaft design Zqna
Zqna Relative motion analysis velocity
Relative motion analysis velocity Compared to a gear tooth on the rear sprocket
Compared to a gear tooth on the rear sprocket Function of dust shield in microscope
Function of dust shield in microscope Function of pillar in microscope
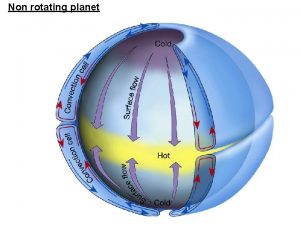
Function of pillar in microscope Non rotating planet
Non rotating planet Magnifying illuminating and mechanical parts of microscope
Magnifying illuminating and mechanical parts of microscope Define suspension culture
Define suspension culture Locomotor in dance
Locomotor in dance A disk initially rotating at 120 rad/s
A disk initially rotating at 120 rad/s Rotating cube display
Rotating cube display