QUANTUM MECHANICS BIRTH OF QUANTUM MECHANICS WAVE PARTICLE

QUANTUM MECHANICS BIRTH OF QUANTUM MECHANICS

WAVE – PARTICLE DUALITY • Let’s revisit Dr. Quantum • https: //www. youtube. com/watch? v=Df. Pepr. Q 7 o. Gc • So, now that we know this happens, we need to ask ourselves, what lead physicists down the path to recognize that EMR can act as both a wave and a particle.

END OF AN ERA • At the end of the 1800 s, physicists looked back at a period of 300 years of great growth. • Newton had explained the motion of objects here on earth (and in the heavens). • Maxwell had put together electricity and magnetism in his work on electromagnetic radiation. What he came up with is what an EMR is and how it works. • Thomson had figured out the mass of atomic particles and so much more! • For the most part, Physicist believed they have solved all the problems of the universe – but things were going to get even more complex than they ever imagined.

CLASSICAL PHYSICS • Up to now, what we have been studying is known as classical physics: • • • Kinematics Dynamics Momentum Energy Waves Mechanics • For almost all physical interactions in the universe we are able to solve using classical physics, but classical physics was unable to solve a few physical (and chemical) problems: • Blackbody Radiation • Photoelectric

EMR WAVE • The red part of the wave is the electric field. • When an electric field is created a magnetic field (the blue part), which is perpendicular to the electric field, is created. • As such we get this wave that is made up of two waves. • This is an Electromagnetic Wave.
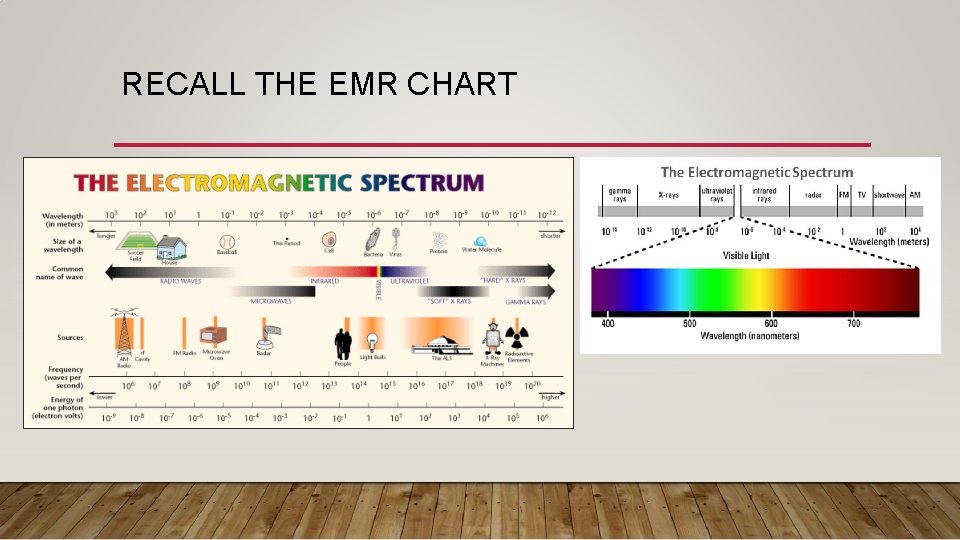
RECALL THE EMR CHART

BLACKBODY RADIATION • A blackbody is an object that perfectly absorbs all wavelengths of EMR that strike it. We humans are a blackbody as we absorb all the wavelengths of EMR from any light. • This means that all EMR, from the lowest frequency to the highest frequency will perfectly be absorbed by the object. • Note it is called a blackbody, since objects colored black absorb all visible light that falls on them. As such the word Blackbody seemed to fit well. Cavity Radiation AKA Blackbody Radiation

BLACKBODY RADIATION • This energy that is absorbed is also perfectly re-emitted and released by the object as EMR. • According to classical physics, as the frequency of the emitted EMR increases, so should the intensity (the vibration of the atoms in the object). • As more and more energy from the EMR was absorbed, it would cause the atoms of the blackbody to vibrate faster and faster at higher and higher frequencies. • These vibrating atoms (made of charged particles) would release higher and higher frequencies of more and more intense EMR.

BLACKBODY RADIATION • Buuuuuuuttttt……. The problem is, this doesn't happen! • Instead, the intensity of the EMR onto the black body object does increase, until it reaches a particular frequency, it (the black body object) then emits radiation at a lower level. • STOP AND THINK – if you are bombarded by UV radiation, are you emitting UV radiation? No we do not. In fact, we actually emit infrared radiation only. • This is bizarre because it flies in the face of what wave theory suggests should happen. • Ultimately, if you are bombarded with radiation that has an infrared radiation, you will absorb it and emit infrared radiation. But if you are bombarded by gamma rays, you will NOT emit gamma rays.
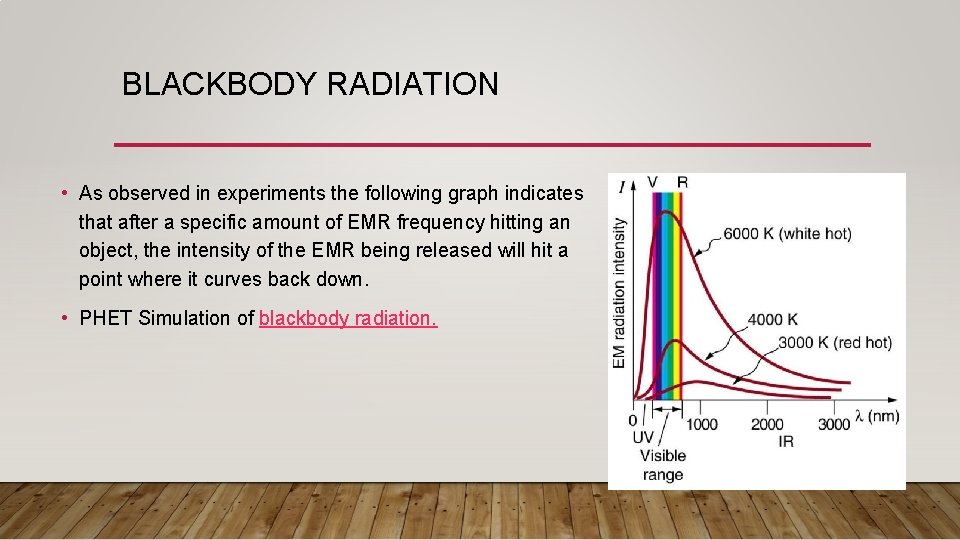
BLACKBODY RADIATION • As observed in experiments the following graph indicates that after a specific amount of EMR frequency hitting an object, the intensity of the EMR being released will hit a point where it curves back down. • PHET Simulation of blackbody radiation.
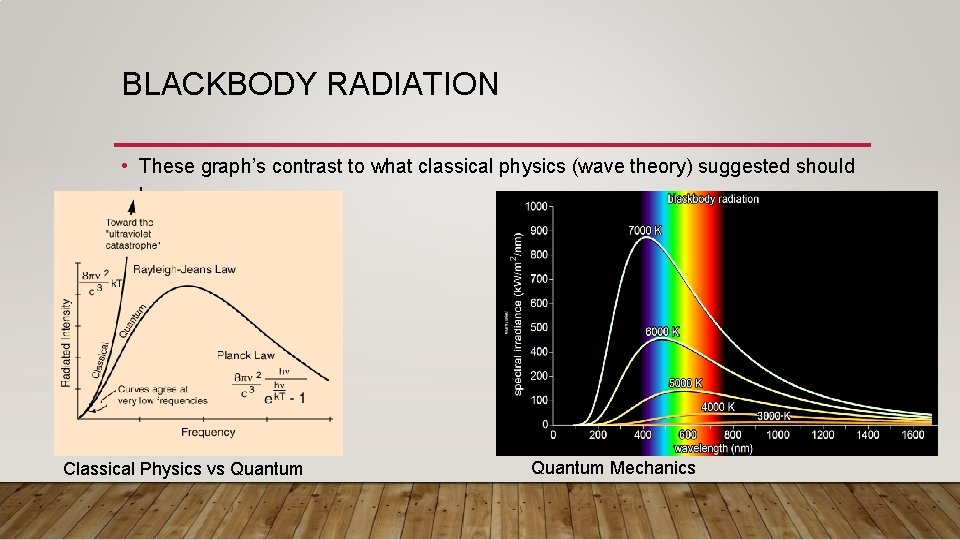
BLACKBODY RADIATION • These graph’s contrast to what classical physics (wave theory) suggested should happen. Classical Physics vs Quantum Mechanics

SOLVING THE BLACKBODY RADIATION PROBLEM • Late in the year 1900, Max Planck (pronounced “Plonk, ”) came up with a new idea that would solve the problems everyone was having when trying to explain blackbody radiation. • Up to this point everyone was assuming that those little vibrating electrons (thought to be absorbing and then re-emitting radiation from a blackbody) could vibrate at any frequency.

PLANCK’S THEORY • Planck suggested that the EMR emitted or absorb by the blackbody was not in a continuous stream of waves but in discrete little bundles - or in separate packets of energy which he called “ quanta”. energy • Planck noted that the Energy of these packets of energy where proportional to their frequencies. As the frequency increased, the energy increased as well.

ENERGY OF VIBRATION/PHOTON • E = nhf • WHERE E = Energy in Joules or e. V n = number of photons, nth state of vibration energy level of orbits in an atom. h = Planks constant – 6. 626 x 10 -34 J · s OR 4. 14 x 10 where 1 e. V = 1. 602677 x 10 -19 J 15 -e. V· s f = is the frequency of vibration of the atom in Hertz (Hz) or 1/s • Note Planks constant can be used in J · s or in e. V s. • So we need a bit of a side bar…. The electron volt.

ELECTRON VOLT • The electron volt, symbol e. V, is used to measure energy. It is like a Joule, but measured as an e. V in energy. • It is defined as the amount of energy an electron gains after being accelerated by 1 volt of electricity. • Joules are used often for energy measurement, but it is sometimes useful to use electron volts for very small amounts of energy. • To convert joules it is important to note that 1 e. V = 1. 602× 10− 19 J • Convert 5 J into e. V 5 J = x ev 1. 602× 10− 19 J = 1 ev 5 J = 3. 12 x 1019 e. V.
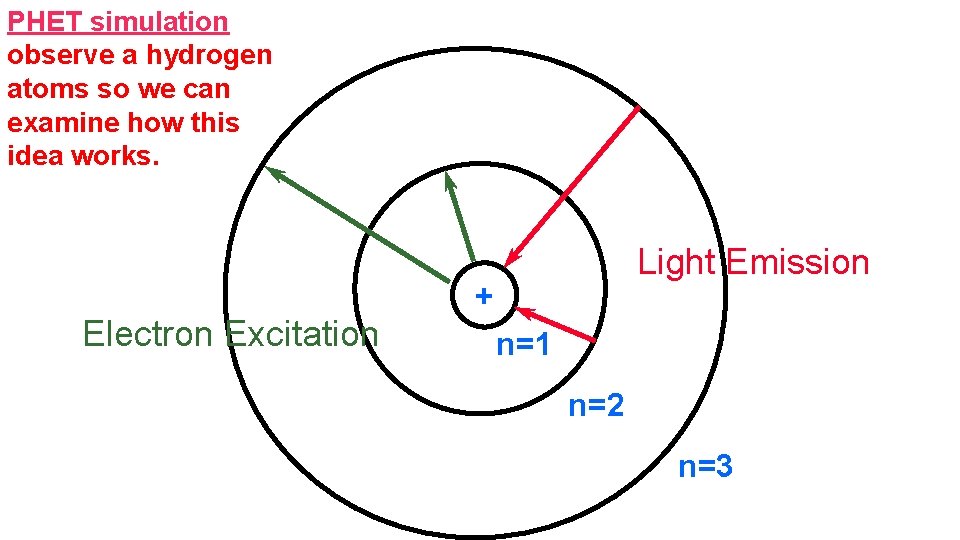
PHET simulation observe a hydrogen atoms so we can examine how this idea works. Electron Excitation Light Emission + n=1 n=2 n=3

ENERGY LEVELS • Ephoton = |Ef – Ei| • If the energy of the photon is greater than the energy of the electron (in a particular orbit) than it will excite the electron. Once the electron goes back to its original orbit, it will release an EMR

PLANKS EQUATION • Planks Equation really solves how much energy a photon (or the packet of waves) has and it can be rewritten as follows: E = hf WHERE E = Energy in Joules or e. V h = Planks constant – 6. 626 x 10 -34 J · s OR 4. 14 x 10 15 -e. V· s where 1 e. V = 1. 602677· 10 -19 J f = is the frequency of vibration of the atom in Hertz (Hz) or 1/s

EXAMPLE # 1 • Determine the smallest amount of energy from a light source that emits light at a frequency of 4. 50 x 1014 Hz. E = hf E = (6. 63 x 10 -34 J · s) (4. 50 x 1014 1/s) E = 2. 9835 x 10 -19 J = 2. 98 x 10 -19 J

EXAMPLE #2 •

ALBERT EINSTEIN • In 1905 an unknown physicist named Albert Einstein came up with an idea that built on Planck’s theory. • Planck thought that his ideas of quanta and E = hf was all about how matter absorbed and emitted energy. • Remember, he was focused on explaining blackbody radiation. • Einstein suggested that these ideas were primarily about the light itself. • He figured that light itself was where it all started, that the light itself was made up of individual pieces. • The reason this was so radical an idea was because it meant that light was acting like a particle. • The light particles were eventually named photons.

A PHOTON • Photon is defined as a particle with zero mass consisting of a quantum of electromagnetic radiation where its energy is concentrated. Photon Energy of waves are quantized into discrete packets of energy. Quantum means “fixed amount”

EXAMPLE #3 • You buy a laser at the store and read on the label that it has a frequency of 4. 38 x 10 15 Hz. The label also says that it runs at 4. 06 m. W (miliwatt). Determine how many photons it can release in one second. • First, determine how much energy the laser can put out in one second, then use Planck’s equation E=nhf and solve for ’n’ the number of photons. P=ΔE/t Δ E=Pt ΔE = (4. 06 x 10 3 -W)(1 s) = 4. 06 x 10 3 - J E=nhf n= E/hf n= 4. 06 x 10 3 -J/ (6. 63 x 1034 - J · s )4. 38) x 1015 1/s ( n=1. 3981005 x 1015 photons 1. 40 x 10 15 photons

ENERGY AND ELECTRON VOLTS • 1 volt is equal to what we call 1 e. V of energy. • Since E = hc/λ some scientists felt it necessary to have energy read in e. V nm for every wavelength. • If we take the hc from our E = hc/λ and convert it into an e. V nm we do this • hc = (6. 626 x 10 -34 J· s)(2. 998 x 10 8 m/s)( 1 ev ) (109 nm) 1. 602 x 10 -19 J 1 m • hc = 1240 e. V nm • As such E = 1240 e. V nm λ 1 ev = 1. 602 x 10 -19 Convert m into nm conversion

EXAMPLE #4 • What is the energy of a 200 nm, 700 nm, and a 1400 nm wavelength in e. V? What happens to the Energy as the wave length gets larger? 200 nm 700 nm 1400 nm E = 1240 e. V nm λ E = 1240 ev nm 200 nm E = 1240 ev nm 700 nm E = 1240 ev nm 1400 nm E = 6. 22 e. V E = 1. 77 e. V E = 0. 89 e. V • As the wave length increases the less energy it has.

ASSIGNMENT • Page 734 Q 1 – 3 • Handout Questions • https: //www. physicsoftheuniverse. com/topics_quantum_quanta. html •
- Slides: 26