Postulates of Quantum Mechanics 1 Normalized ket vector






















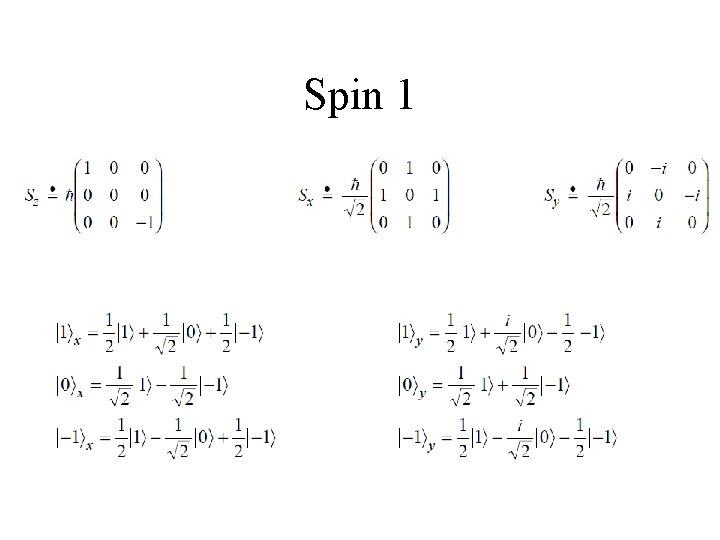








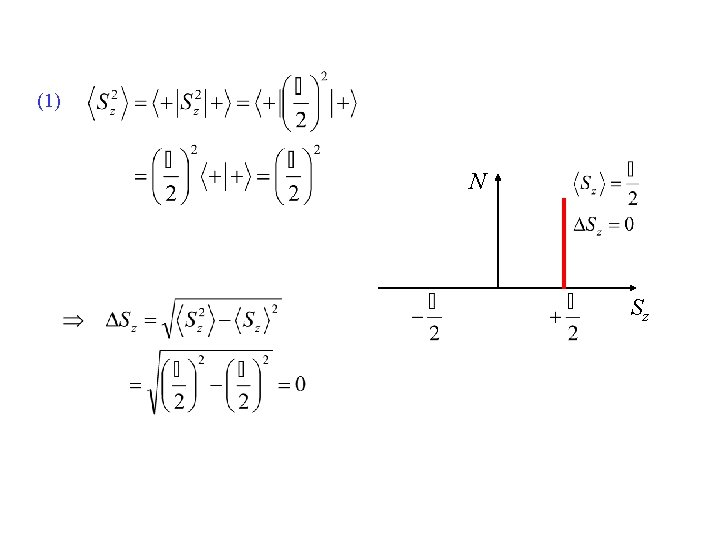









- Slides: 45

Postulates of Quantum Mechanics 1. Normalized ket vector contains all the information about the state of a quantum mechanical system. 2. Operator A describes a physical observable and acts on kets. 3. One of the eigenvalues an of A is the only possible result of a measurement. 4. The probability of obtaining the eigenvalue an : 5. State vector collapse : 6. Schrödinger Equation : Time evolution of a quantum system

Sz is the operator that corresponds to the physical observable of spin along the z-axis. Write the eigenvalue equation for Sz using the above notation Write the matrix Sz, and the kets |+> and |-> in matrix notation



In the z-basis, use what we know about how to write the kets |+>x and so on (given below) to find the matrices Sy and Sx










Group work • Show that the Sx, Sy and Sz matrices can be written as a linear combination of projection operators. (Projection operators are outer products of the eigenvectors with themselves. ) The coefficient of each term is the eigenvalue associated with the eigenvector used to make the projection operator.

Postulates of Quantum Mechanics 1. Normalized ket vector contains all the information about the state of a quantum mechanical system. 2. Operator A describes a physical observable and acts on kets. 3. One of the eigenvalues an of A is the only possible result of a measurement. 4. The probability of obtaining the eigenvalue an : 5. State vector collapse : 6. Schrödinger Equation : Time evolution of a quantum system

What do we know so far? • Atoms (and fundamental particles, i. e. , electrons) can have “intrinsic spin” – can be a 2 -level spin system, where all measurements of the intrinsic angular momentum yield + or – hbar/2 • Can measure this with S-G device • Find that by looking at the % of atoms found along different spin projections (i. e. Sz) we can infer the initial state • Find that making a measurement to determine the state of an atom changes the state -> “collapses” the atom into the new state – this is related to “projection”

Group work • Show that the spin operator matrices: Sx and Sy can be written as a linear combination of projection operators, where the projection operators are outer products of the eigenvectors with themselves and the coefficient of each term is the eigenvalue associated with the eigenvector used to make the projection operator • If a spin operator acts on a vector, what transformation does it correspond to?

Hermetian Operators: At = A • We normalize the eigenkets! • ALWAYS have real eigenvalues and orthogonal eigenfunctions that form a complete basis set • Linear transformations – What kind of transformations have you observed with matrices acting on vectors – what do they do? – Come up with at least one “physical” example of a linear transformation (operator) (you don’t need to write the matrix, just say what it does) – What did the projection operators do to the vectors? – What can you say about the operators Sz, Sx, and Sy?

Projection operator • Operators “embed” the kets and eigenvalues • The projector operator MODELS measurements – it tells us what state (ket) the atom is in after the measurement: • It tells us about the probability of finding a particular eigenvalue from a measurement • P+|ψ> = |+><+| ψ> = ψ+|+> = coefficient of Psi along +z spin, in the +z spin direction (this new ket is NOT normalized!)

“Fixing our equation” to make the new ket always normalized

Spin 1 systems: • Spin measurements can be h, 0 or –h (h = hbar) • Write the eigenvalue equations for Sz • Write the operator Sz in matrix form, and the kets corresponding to spin-up in Z, spin 0 in Z, and spin-down in Z
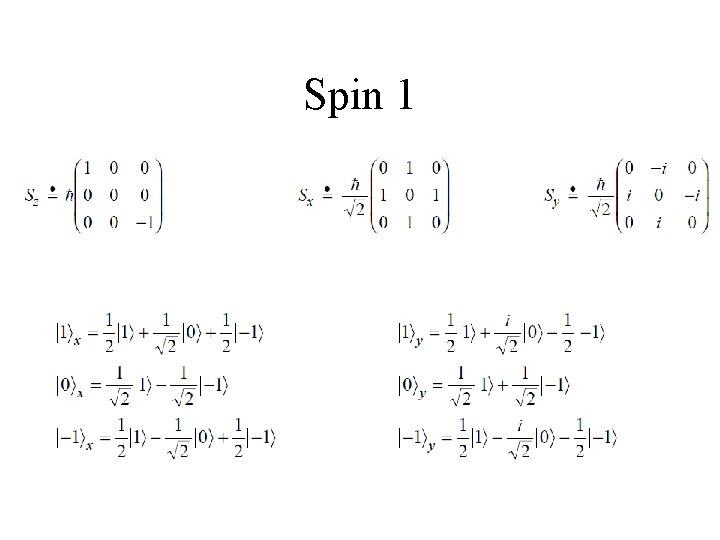
Spin 1

Small board activity • As a class you’ll calculate all combinations of Sx, Sy, and Sz operators acting on all the eigenstates: |+>, |->, |+>x, |->x, |+>y, |->y, and we’ll try to determine what this operation “does” • • There are 18 combinations – each of you will do 2 Count off by 9’s 1’s do Sx on |+> and |->x 2’s do Sx on |-> and |+>y 3’s do Sx on |+>x and |->y 4’s are like 1 with Sy, 5’s like 2 with Sy, 6 like 3 with Sy 7 like 1 with Sz, 8 like 2 with Sz, 9 like 3 with Sz

Your General questions: • How do we know how many eigenvalues a matrix has? • What is “COLLAPSING”? (Copenhagen vs. multiverse) • What “ARE” operators, and what do they do? (better question: what do Hermitian operators represent? ) • Don’t all measurements “perturb” a system? • Is this the same phenomena except at very small scales the perturbation is large? • Is “quantization” odd? • What is a basis, and when do we have to be in a particular basis? • Should some calculations be basis independent, and does that mean we don’t have to be careful?

2. 2 Measurement When doing a Quantum measurement, making a measurement changes the state Is this really so odd? Two examples: determining the classical trajectory of an object (handout) Illuminate it to see where it is (optical method) • Radiation pressure will disturb the motion • If we want to disturb it less, we have to radiate it less – this means we’ll know less about the position • We can reduce the intensity of the light to individual photos to minimize the disturbance – but then can go no lower • We can reduce the energy of the photons by increasing the wavelength – but that reduces our resolution Mechanical method – use a series of bells • If the bells are too large there is low resolution • If the bells are too small there will be too much momentum transfer and we’ll disturb the projectile • (This type of measurement is analogous to a tracking chamber in a particle physics experiment)

Tracking chamber (the inner blue ring on right – note scale of person)

BOTH classical and quantum measurements perturb a system and have a fundamental interplay between “resoultion” and “perturbation” (x and p) What is different between classical and quantum measurement? • Classical: a single measurement can be compared to theory, multiple measurements simply reduce the systematic and measurement errors • Quantum: a single measurement tells us something about the eigenvalues, but does not tell us about the original state or tell us that a similar measurement will yield the same result • MORE and MORE measurements do not minimize uncertainty in quantum measurements! It’s all probabilistic! • We will need to apply statistics to understand our measurements! Example: Single measurement of Sz cannot determine the original state, and can result in more than one value! |+ X |+ x Prepare atoms in a particular state N+ Z |- N=N++N- NPerform the same experiment on each identically prepared atom

Expectation Value (also called the mean or average) The expected mean value of a large number of experiments THIS IS NOT the expected value of any single experiment!! THIS IS NOT a time average – it is an average over many identical experiments!! Example: rolling dice We expect an average value different from any individual measurement In words: the MEAN result of a measurement will be value x, X% of the time plus value y, Y% of the time

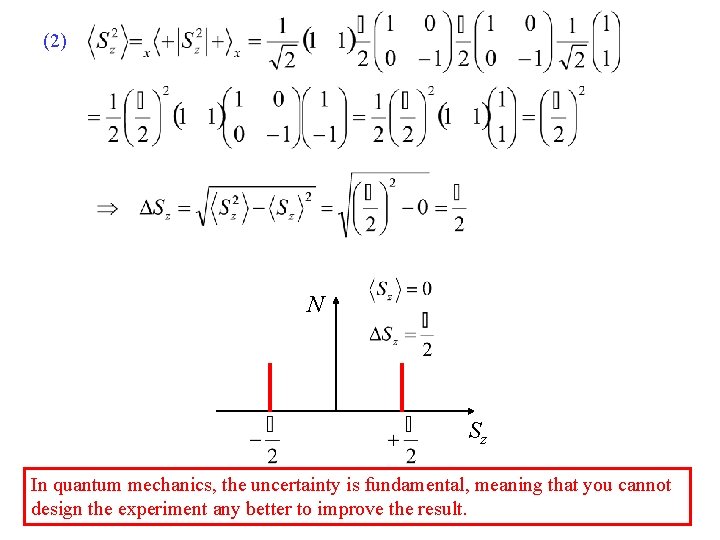
What do we expect to get if we take the expectation value of Sz for a system prepared in state |+ ? Do the calculation on your whiteboards! Only possible result: this must be the expectation value. (1) Or we could do the full calculation: (1 0) h 1 0 2 0 -1 1 0 What do we expect to get if we take the expectation value of Sz for a system prepared in state |+ x ? Let’s calculate it! (2) The two possible results ± heach have 50% possibility, 2 so we’d find h(. 5) + - h(. 5) = 0 2 2

Standard Deviation: spread of measurements about the mean General Formula written in QM notation: • What does the thing under the square root mean? • Why do we square then take the square root? • (What would we get if we didn’t take the square? ) -> Let’s simplify this expression by expanding it out Let’s find this for the two previous examples: What do you expect for the standard deviation of the measurement for Sz in state |+ ? What do we find? What do you expect for the standard deviation of the measurement for Sz in state |+ x? What do we find?
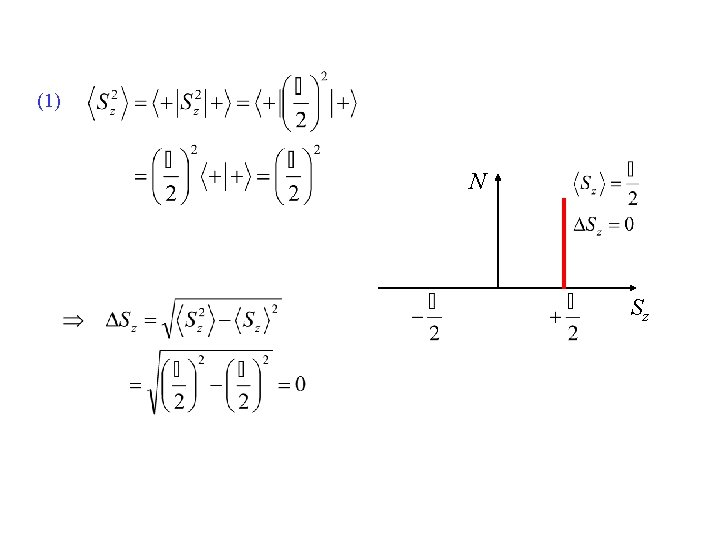
(1) N Sz

(2) N Sz In quantum mechanics, the uncertainty is fundamental, meaning that you cannot design the experiment any better to improve the result.

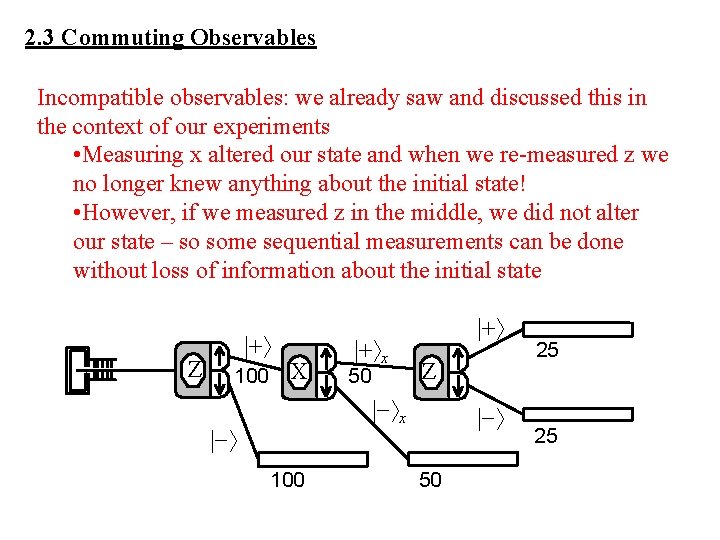
2. 3 Commuting Observables Incompatible observables: we already saw and discussed this in the context of our experiments • Measuring x altered our state and when we re-measured z we no longer knew anything about the initial state! • However, if we measured z in the middle, we did not alter our state – so some sequential measurements can be done without loss of information about the initial state Z |+ 100 X |+ x 50 |+ Z |- x |- 100 |- 50 25 25

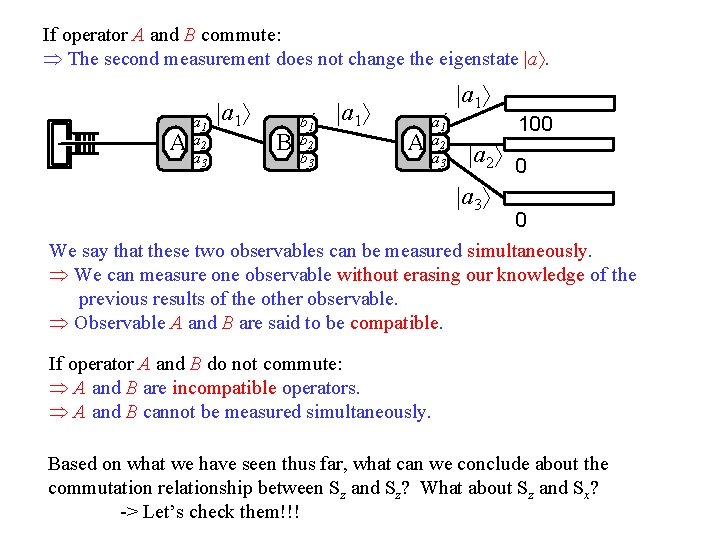
Commuting property in mathematics: if A and B commute, then AB = BA Commutator: Operator A and B commute if [A, B]=0. AB-BA=0 AB=BA Let |a be an eigenstate of the operator A with eigenvalue a: If A and B Commute: We get another Eigenvalue equation With eigenvector B|a> an eigenstate of A with the same eigenvalue a BA a = Ba a AB a = a. B a We can move out our constant a A(B a ) = a(B a ) So B|a> must be a scalar multiple of |a> ! IF Operator A and B commute THEN A and B have common (or simultaneous) sets of eigenstates.

If operator A and B commute: The second measurement does not change the eigenstate |a. A a 1 a 2 a 3 |a 1 B b 1 b 2 b 3 |a 1 A a 1 a 2 a 3 100 |a 2 0 |a 3 0 We say that these two observables can be measured simultaneously. We can measure one observable without erasing our knowledge of the previous results of the other observable. Observable A and B are said to be compatible. If operator A and B do not commute: A and B are incompatible operators. A and B cannot be measured simultaneously. Based on what we have seen thus far, what can we conclude about the commutation relationship between Sz and Sz? What about Sz and Sx? -> Let’s check them!!!

Example: These two operators do not commute. Time permitting – let’s check another one (this problem was removed from your homework assignment – let’s make sure we can all do this calculation) None of the spin projection observables commute each other – DO THESE IN CLASS!!!.

2. 4 Uncertainty Principle Example: If the initial state is |+ , Recall ΔSz is zero for this case! • If we knowzspin along one direction, we don’t know it along the other directions: we can never know two non-commuting observables simultaneously!! • Spin does NOT point in a specific direction. Our classical image of spin does not work! We can only know a projection of it onto one axis at a time! y • “Spin up” means that spin projection along that axis is up. x

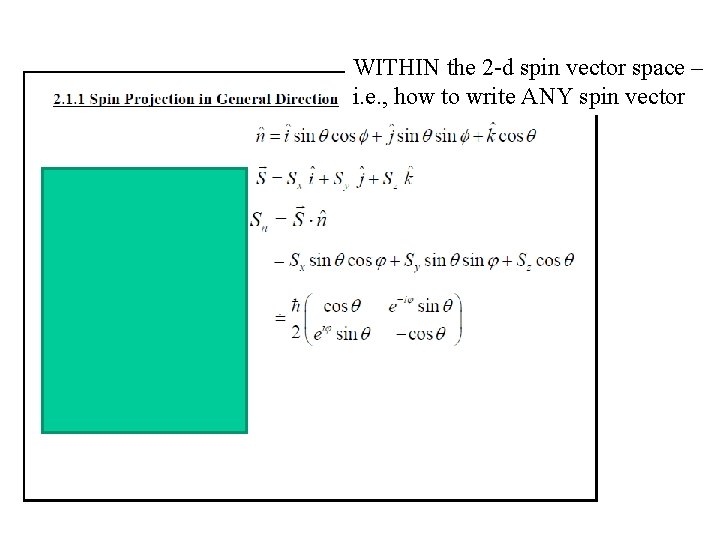
(no time left for this – see book for derivation) Group white boards • Write a general unit vector in spherical coordinates that can point anywhere in 3 -d space (this vector is usually called n ) • If a total spin vector S can be written as Sxi + Syj + Szk , write S (dot) n • What operator might this correspond to? • Check what it might correspond to by putting in specific values for theta and phi (pointing n in specific known directions)

WITHIN the 2 -d spin vector space – i. e. , how to write ANY spin vector

No matter which way the spin vector “points” – what will we measure? ?

2. 5 S 2 Operator: As with any vector, if we square it we have information about the magnitude but we loose information about the direction! 2 ( æ hö 2 2 2 = + + = S S x S y S z ç ÷ s x + s y 2 + s z 2 è 2ø Find S 2 in matrix form ) What operators will S 2 commute with? What can we conclude about simultaneously knowing the value of S 2 and the projection of S along x, y or z? What are the eigenstates of the operator S 2? What are the eigenvalues? What is the expectation value of S 2? What can you deduce about the “length” of the spin vector?

For any |y in the spin-1/2 system NOT just our eigenstates of Sx, Sy and Sz The spin vector is longer than any of the measured projections (ħ/2): the full spin vector can never be fully aligned along any axis!! z y x This vector describes the "direction" in which the spin is pointing, corresponding to the classical concept of the axis of rotation. The spin vector does have a well-defined experimental meaning: It specifies the direction in ordinary space in which a subsequent detector must be oriented in order to achieve the maximum possible probability (100%) of detecting every particle in the collection. For spin-1/2 particles, this maximum probability drops off smoothly as the angle between the spin vector and the detector increases, until at an angle of 180 degrees — that is, for detectors oriented in the opposite direction to the spin vector—the expectation of detecting particles from the collection reaches a minimum of 0%.

YOUR awesome words: • As was so clearly stated by your comments in class: • IF spin were in 3 -d physical space, then we could in principle align our S-G device along S and measure the full value of root(3)/2 hbar – but we can NEVER measure that value – we can only measure the projections hbar/2 at any one time!

Generalize to other spin systems: • s = spin quantum number- the “spin” of the system, such as ½ in what we’ve done so far • m = the projection of the spin (magnetic quantum number) – it can take on values from –s to s in integer steps Our spin-1/2 system in this notation: Write down what some states can look like for a spin 3/2 system