Postulates and General Principles of Quantum Mechanics Erwin

Postulates and General Principles of Quantum Mechanics

Erwin Schrödinger— In 1926 wrote a wave equation taking into account the wave-particle duality (de Broglie) and the Uncertainty principle (Heisenberg)

The Schrödinger Equation The fundamental equation of Quantum Mechanics Solutions to the Schrödinger equation are called wavefunctions We begin by the time-independent Schrödinger Equation yielding Stationary-State Wavefunctions We cannot really derive the Schrödinger Equation The Equation is regarded as a fundamental postulate or Axiom of Quantum Mechanics But we can perhaps trace back the original line of thought One story: at some meeting, it was suggested that there must be a wave equation that governs matter if it has wave properties

Start with the 1 D wave equation can also write T(t)=e 2 i t (x)=spatial amplitude Cos: time dependence Replace, get time-independent eqn Here introduce the idea of de Broglie waves for matter p=h/ =mv

Including de-broglie wave-particle duality Replace into the wave equation: 1 D time-independent Schrödinger Equation

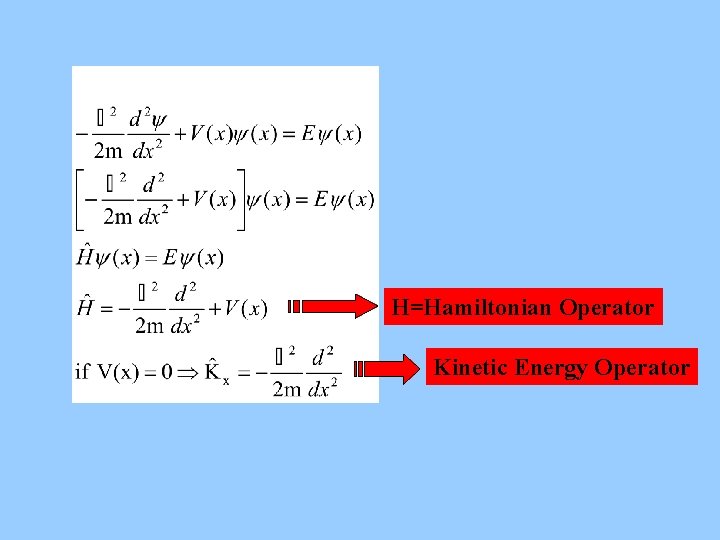
3 D time-independent Schrödinger Equation Laplacian Operator

Operators • An operator is a symbol that tells you to do a mathematical operation on the function that follows the symbol In QM we deal with linear operators A is linear: A[c 1 f(x)+c 2 f(x)]=c 1 Af(x)+c 2 Af(x) Examples: “differentiate” and “integrate” operators

Eigenfunction, eigenvalue problem

H=Hamiltonian Operator Kinetic Energy Operator

time-independent Schrödinger Equation is an eigenvalue problem:

Postulate 1. • The state of a quantum mechanical system is fully specified by a function (x) or (x, y, z) that depends upon the coordinate(s) of the particle. All possible information can be derived from . • This function, called the wavefunction, has the important property that (x) *(x) dx [when (x) is normalized] is the probability that the particle lies in the interval dx located at the position x. Or in 3 D that (x, y, z) *(x, y, z)dxdydz is the probability that the particle lies in the volume element dxdydz at position x, y, z

The Born Interpretation of the wavefunction: • It is a principal tenet of Q. M. that the wavefunction contains all dynamical information about the system it describes. • Interpretation of Max Born: in analogy with the wave theory of light where the intensity is proportional to the square of the amplitudes of the electric and magnetic fields; “intensity” in quantum mechanics is a measure of the probability. . therefore the probability is proportional to the square of the wavefunction. . If is normalized

Normalization • is a solution, therefore N. is a solution • We can find a constant N so that the Born interpretation becomes an equality

Conditions on • The wavefunction cannot be infinite over a finite region in space, if it did which can’t be. unacceptable x • It must be single valued: it is absurd that there will be 2 probabilities of finding the particle in space unacceptable x • Because the equation is a second order equation, the 2 nd derivative must exist so the function must be continuous unacceptable x

Postulate 2. Quantum Mechanical Operators • To every observable in classical mechanics there corresponds a linear hermitian operator in quantum mechanics. (the operators are chosen to satisfy the commutation relationship: ) • One begins to write the classical expression as fully as possible in terms of momentum and position:

See Table 4. 1 Mc. Quarrie, p. 119 for a summary of operators in 1 D and 3 D. Note vector notation using unit vectors i, j, k. We will learn about angular momentum later. . . )

Hermitian operators • The class of operators called hermitian operators plays a special role in QM. Hermitian operators have real eigenvalues, and hence correspond to an observable (the outcome of an experiment must be real).

Dirac Bracket Notation: Bra (< I): conjugate cket (I >): function itself Hermiticity condition in Dirac Bracket Notation is:

Properties of hermitian operators • Property 1: the eigenvalues of hermitian operators are real • Property 2: the eigenstates corresponding to the different eigenvalues of hermitian operators are orthogonal

Orthogonality: Example: 2 wavefunctions corresponding to different energies are orthogonal. Orthonormality:

Homework due on Tuesday February 7: Show that (1) eigenvalues of hermitian operators are real and (2) that the eigenstates corresponding to different eigenvalues of Hermitian operators are orthogonal

• Show that the momentum operator Px is Hermitian. Hint: vanishes at end points