Postulates of Quantum Mechanics SOURCES Angela Antoniu David

Postulates of Quantum Mechanics SOURCES Angela Antoniu, David Fortin, Artur Ekert, Michael Frank, Kevin Irwig , Anuj Dawar , Michael Nielsen Jacob Biamonte and students

Short review Linear Operators • V, W: Vector spaces. • A linear operator A from V to W is a linear function A: V W. An operator on V is an operator from V to itself. • Given bases for V and W, we can represent linear operators as matrices. • An operator A on V is Hermitian iff it is self-adjoint (A=A†). • Its diagonal elements are real.

Eigenvalues & Eigenvectors • v is called an eigenvector of linear operator A iff A just multiplies v by a scalar x, i. e. Av=xv – “eigen” (German) = “characteristic”. • x, the eigenvalue corresponding to eigenvector v, is just the scalar that A multiplies v by. • the eigenvalue x is degenerate if it is shared by 2 eigenvectors that are not scalar multiples of each other. – (Two different eigenvectors have the same eigenvalue) • Any Hermitian operator has all real-valued eigenvectors, which are orthogonal (for distinct eigenvalues).

Exam Problems • • • Find eigenvalues and eigenvectors of operators. Calculate solutions for quantum arrays. Prove that rows and columns are orthonormal. Prove probability preservation Prove unitarity of matrices. Postulates of Quantum Mechanics. Examples and interpretations. • Properties of unitary operators

Unitary Transformations • A matrix (or linear operator) U is unitary iff its inverse equals its adjoint: U 1 = U† • Some properties of unitary transformations (UT): – – Invertible, bijective, one-to-one. The set of row vectors is orthonormal. The set of column vectors is orthonormal. Unitary transformation preserves vector length: |U | = | | • Therefore also preserves total probability over all states: – UT corresponds to a change of basis, from one orthonormal basis to another. – Or, a generalized rotation of in Hilbert space Who an when invented all this stuff? ?

A great breakthrough

Postulates of Quantum Mechanics Lecture objectives • Why are postulates important? – … they provide the connections between the physical, real, world and the quantum mechanics mathematics used to model these systems • Lecture Objectives – Description of connections – Introduce the postulates – Learn how to use them – …and when to use them

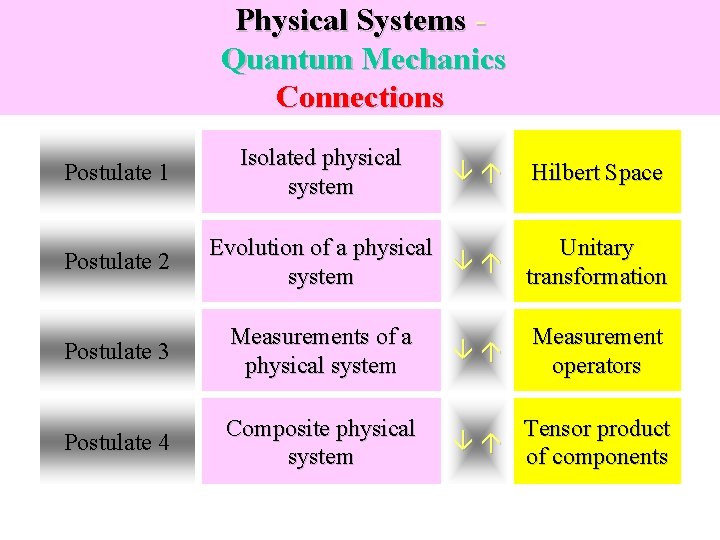
Physical Systems Quantum Mechanics Connections Postulate 1 Postulate 2 Isolated physical system Hilbert Space Evolution of a physical system Unitary transformation Postulate 3 Measurements of a physical system Measurement operators Postulate 4 Composite physical system Tensor product of components

Postulate 1: State Space

Systems and Subsystems • Intuitively speaking, a physical system consists of a region of spacetime & all the entities (e. g. particles & fields) contained within it. – The universe (over all time) is a physical system – Transistors, computers, people: also physical systems. • One physical system A is a subsystem of another system B (write A B) iff A is completely contained within B. A • Later, we may try to make these definitions more formal & precise. B

Closed vs. Open Systems • A subsystem is closed to the extent that no particles, information, energy, or entropy enter or leave the system. – The universe is (presumably) a closed system. – Subsystems of the universe may be almost closed • Often in physics we consider statements about closed systems. – These statements may often be perfectly true only in a perfectly closed system. – However, they will often also be approximately true in any nearly closed system (in a well-defined way)

Concrete vs. Abstract Systems • Usually, when reasoning about or interacting with a system, an entity (e. g. a physicist) has in mind a description of the system. • A description that contains every property of the system is an exact or concrete description. – That system (to the entity) is a concrete system. • Other descriptions are abstract descriptions. – The system (as considered by that entity) is an abstract system, to some degree. • We nearly always deal with abstract systems! – Based on the descriptions that are available to us.

States & State Spaces • A possible state S of an abstract system A (described by a description D) is any concrete system C that is consistent with D. – I. e. , it is possible that the system in question could be completely described by the description of C. • The state space of A is the set of all possible states of A. • Most of the class, the concepts we’ve discussed can be applied to either classical or quantum physics – Now, let’s get to the uniquely quantum stuff…

An example of a state space

Schroedinger’s Cat and Explanation of Qubits Postulate 1 in a simple way: An isolated physical system is described by a unit vector (state vector) in a Hilbert space (state space) Cat is isolated in the box

Distinguishability of States • Classical and quantum mechanics differ regarding the distinguishability of states. • In classical mechanics, there is no issue: – Any two states s, t are either the same (s = t), or different (s t), and that’s all there is to it. • In quantum mechanics (i. e. in reality): – There are pairs of states s t that are mathematically distinct, but not 100% physically distinguishable. – Such states cannot be reliably distinguished by any number of measurements, no matter how precise. • But you can know the real state (with high probability), if you prepared the system to be in a certain state.

Postulate 1: State Space – Postulate 1 defines “the setting” in which Quantum Mechanics takes place. – This setting is the Hilbert space. – The Hilbert Space is an inner product space which satisfies the condition of completeness (recall math lecture few weeks ago). • Postulate 1: Any isolated physical space is associated with a complex vector space with inner product called the State Space of the system. – The system is completely described by a state vector, a unit vector, pertaining to the state space. – The state space describes all possible states the system can be in. – Postulate 1 does NOT tell us either what the state space is or what the state vector is.

Distinguishability of States, more precisely • Two state vectors s and t are (perfectly) distinguishable or orthogonal t (write s t) iff s†t = 0. (Their inner product is zero. ) s • State vectors s and t are perfectly indistinguishable or identical (write s=t) iff s†t = 1. (Their inner product is one. ) • Otherwise, s and t are both non-orthogonal, and non-identical. Not perfectly distinguishable. • We say, “the amplitude of state s, given state t, is s†t”. – Note: amplitudes are complex numbers.

State Vectors & Hilbert Space • Let S be any maximal set of distinguishable possible states s, t, … of an abstract system A. • Identify the elements of S with unit-length, mutuallyorthogonal (basis) vectors in an abstract complex vector space H. – The “Hilbert space” • Postulate 1: The possible states of A can be identified with the unit vectors of H. t s

Postulate 2: Evolution

Postulate 2: Evolution • Evolution of an isolated system can be expressed as: where t 1, t 2 are moments in time and U(t 1, t 2) is a unitary operator. – U may vary with time. Hence, the corresponding segment of time is explicitly specified: U(t 1, t 2) – the process is in a sense Markovian (history doesn’t matter) and reversible, since Unitary operations preserve inner product

Example of evolution

Time Evolution • Recall the Postulate: (Closed) systems evolve (change state) over time via unitary transformations. t 2 = Ut 1 t 2 t 1 • Note that since U is linear, a small-factor change in amplitude of a particular state at t 1 leads to a correspondingly small change in the amplitude of the corresponding state at t 2. – Chaos (sensitivity to initial conditions) requires an ensemble of initial states that are different enough to be distinguishable (in the sense we defined) • Indistinguishable initial states never beget distinguishable outcome

Wavefunctions • Given any set S of system states (mutually distinguishable, or not), • A quantum state vector can also be translated to a wavefunction : S C, giving, for each state s S, the amplitude (s) of that state. – is called a wavefunction because its time evolution obeys an equation (Schrödinger’s equation) which has the form of a wave equation when S ranges over a space of positional states.

Schrödinger’s Wave Equation for particles We have a system with states given by (x, t) where: – t is a global time coordinate, and – x describes N/3 particles (p 1, …, p. N/3) with masses (m 1, …, m. N/3) in a 3 -D Euclidean space, – where each pi is located at coordinates (x 3 i, x 3 i+1, x 3 i+2), and – where particles interact with potential energy function V(x, t), • the wavefunction (x, t) obeys the following (2 nd-order, linear, partial) differential equation: Planck Constant

Features of the wave equation • Particles’ momentum state p is encoded implicitly by the particle’s wavelength : p=h/ • The energy of any state is given by the frequency of rotation of the wavefunction in the complex plane: E=h. • By simulating this simple equation, one can observe basic quantum phenomena such as: – Interference fringes – Tunneling of wave packets through potential barriers

Heisenberg and Schroedinger views of Postulate 2 This is Heisenberg picture This is Schroedinger picture . . in this class we are interested in Heisenberg’s view…. .

The Solution to the Schrödinger Equation • The Schrödinger Equation governs the transformation of an initial input state to a final output state. • It is a prescription for what we want to do to the computer. • is a time-dependent Hermitian matrix of size 2 n called the Hamiltonian • is a matrix of size 2 n called the evolution matrix, • Vectors of complex numbers of length 2 n • Tτ is the time-ordering operator

The Schrödinger Equation • n is the number of quantum bits (qubits) in the quantum computer • The function exp is the traditional exponential function, but some care must be taken here because the argument is a matrix. We discussed this power series already • The evolution matrix is the program for the quantum computer. Applying this program to the input state produces the output state , which gives us a solution to the problem. Formula from last slide

The Hamiltonian Matrix in Schroedinger Equation • The Hamiltonian is a matrix that tells us how the quantum computer reacts to the application of signals. • In other words, it describes how the qubits behave under the influence of a machine language consisting of varying some controllable parameters (like electric or magnetic fields). • Usually, the form of the matrix H needs to be either derived by a physicist or obtained via direct measurement of the properties of the computer.

The Evolution Matrix in the Schrodinger Equation • While the Hamiltonian describes how the quantum computer responds to the machine language, the evolution matrix describes the effect that this has on the state of the quantum computer. • While knowing the Hamiltonian allows us to calculate the evolution matrix in a pretty straightforward way, the reverse is not true. • If we know the program, by which is meant the evolution matrix, it is not an easy problem to determine the machine language sequence that produces that program. • This is the quantum computer science version of the compiler problem. Or “logic synthesis” problem. Evolution matrix Hamiltonian matrix

Postulate 3: Quantum Measurement

Computational Basis – a reminder Observe that it is not required to be orthonormal, just linearly independent We recalculate to a new basis

Example of measurement in different bases 1/ 2 The second with probability zero

• You can check from definition that inner product of |0> and |1> is zero. • Similarly the inner product of vectors from the second basis is zero. • But we can take vectors like |0> and 1/ 2(|0>-|1>) as a basis also, although measurement will perhaps suffer. Good base Not a base

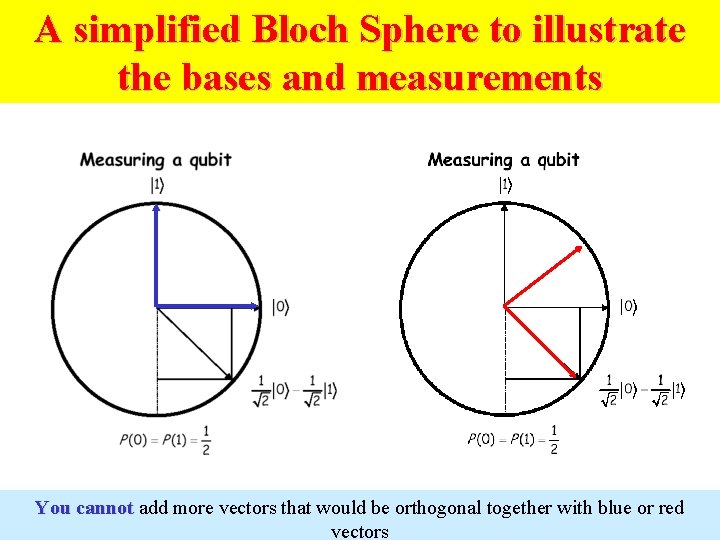
A simplified Bloch Sphere to illustrate the bases and measurements You cannot add more vectors that would be orthogonal together with blue or red vectors

Probability and Measurement • A yes/no measurement is an interaction designed to determine whether a given system is in a certain state s. • The amplitude of state s, given the actual state t of the system determines the probability of getting a “yes” from the measurement. • Important: For a system prepared in state t, any measurement that asks “is it in state s? ” will return “yes” with probability Pr[s|t] = |s†t|2 – After the measurement, the state is changed, in a way we will define later. Inner product between states

A Simple Example of distinguishable, nondistinguishable states and measurements • Suppose abstract system S has a set of only 4 distinguishable possible states, which we’ll call s 0, s 1, s 2, and s 3, with corresponding ket vectors |s 0 , |s 1 , |s 2 , and |s 3. • Another possible state is then the vector • Which is equal to the column matrix: • If measured to see if it is in state s 0, we have a 50% chance of getting a “yes”.

Observables • Hermitian operator A on V is called an observable if there is an orthonormal (all unitlength, and mutually orthogonal) subset of its eigenvectors that forms a basis of V. There can be measurements that are not observables Observe that the eigenvectors must be orthonormal

Observables • Postulate 3: – Every measurable physical property of a system is described by a corresponding operator A. – Measurement outcomes correspond to eigenvalues. • Postulate 3 a: – The probability of an outcome is given by the squared absolute amplitude of the corresponding eigenvector(s), given the state.

Density Operators • For a given state | , the probabilities of all the basis states si are determined by an Hermitian operator or matrix (the density matrix): • The diagonal elements i, i are the probabilities of the basis states. – The off-diagonal elements are “coherences”. • The density matrix describes the state exactly.

Towards QM Postulate 3 on measurement and general formulas A measurement is described by an Hermitian eigenvalue operator (observable) M= m Pm m – Pm is the projector onto the eigenspace of M with eigenvalue m Pm| – After the measurement the state will be p(m) with probability p(m) = |Pm| . – e. g. measurement of a qubit in the computational basis • measuring | = |0 + |1 gives: • |0 with probability |0 0| = | 0| |2 = | |2 • |1 with probability |1 1| = | 1| |2 = | |2 Derived in next slide

An example how Measurement Operators act on the state space of a quantum system Measurement operators act on the state space of a quantum system Initial state: Hadamard Operate on the state space with an operator that preservers unitary evolution: = |0 + |1 Define a collection of measurement operators for our state space: Half probability of measuring 0 Act on the state space of our system with measurement operators: = p 0 Half probability of measuring 1 But now it is a part of formal calculus

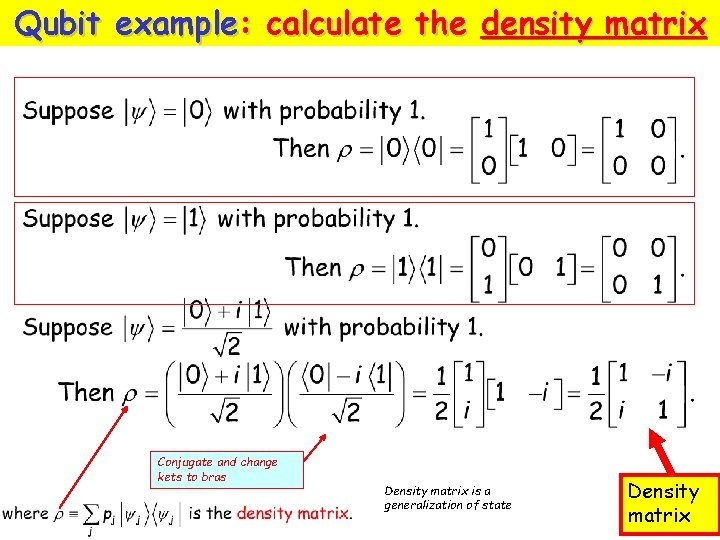
Qubit example: calculate the density matrix Conjugate and change kets to bras Density matrix is a generalization of state Density matrix

Measurement of a state vector using projective measurement Operate on the state space with an operator that preservers unitary evolution: Define observables: Act on the state space of our system with observables (The average value of measurement outcome after lots of measurements): Vector is on axis X This type of measurement represents the limit as the number of measurements goes to infinity Here 3 may be enough, in general you need four

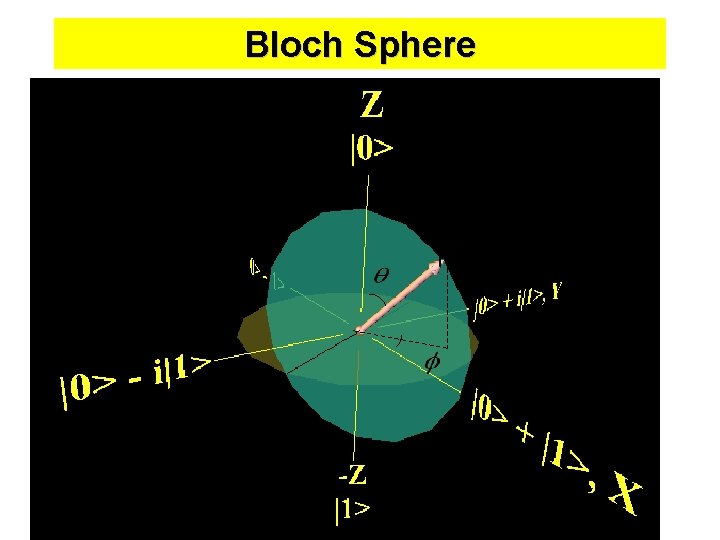
Bloch Sphere

Very General Formula • probability p(m) = |Pm| . Any type of measurement operator “insert Operator between Braket” rule |Pm| = state (column vector) |Pm| = number = probability

More examples and generalizations: Duals and Inner Products are used in measurements < | This is inner product not tensor product! ( ) Remember this is a number We prove from general properties of operators

Review: Duals as Row Vectors To do bra from ket you need transpose and conjugate to make a row vector of conjugates. Do this always if you are in trouble to understand some formula involving operators, density matrices, bras and kets.

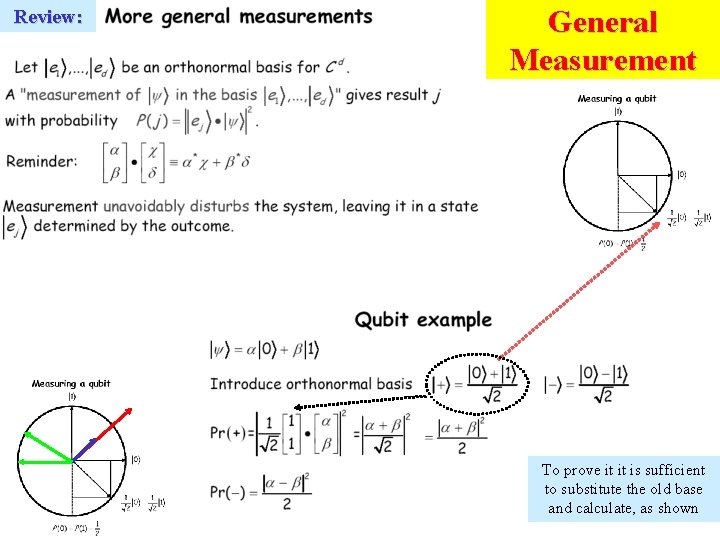
Review: General Measurement To prove it it is sufficient to substitute the old base and calculate, as shown

Illustration of the formalisms used. You can calculate measurements from there q State Vector Density State

Postulate 3, rough form This is calculate as in 2 slides earlier

Mixed States • Suppose only knows of a system that it is in one of a statistical ensemble of state vectors vi (“pure” states), each with density matrix i and probability Pi. • This is called a mixed state. • This ensemble is completely described, for all physical purposes, by the expectation value (weighted average) of density matrices: – Note: even if there were uncountably many state vectors vi, the state remains fully described by <n 2 complex numbers, where n is the number of basis states!

Ensemble of quantum states • Quantum states can be expressed as a density matrix: Sum of these probabilities is one For the ensemble • A system with n quantum states has n entries across the diagonal of the density matrix. The nth entry of the diagonal corresponds to the probability of the system being measured in the nth quantum state. • The off diagonal correlations are zeroed out by decoherence.

Unitary operations on a density matrix • Unitary operations on a density matrix are expressed as: Old density matrix New density matrix adjoint • In other words the diagonal of density matrix is left as weights corresponding to the current states projection onto the computational basis after acted on by the unitary operator U – Much like an inner product.

Trace of Matrix • Trace of a matrix (sum of the diagonal elements): • Unitary operators are trace preserving. • The trace of a pure state is 1, all information about the system is known. • Operators Commute under the action of the trace:

The trace operation

Partial Trace of a Matrix • Partial Trace (defined by linearity) • If you want to know about the nth state in a system, you can trace over the other states. Partial trace Density matrix trace

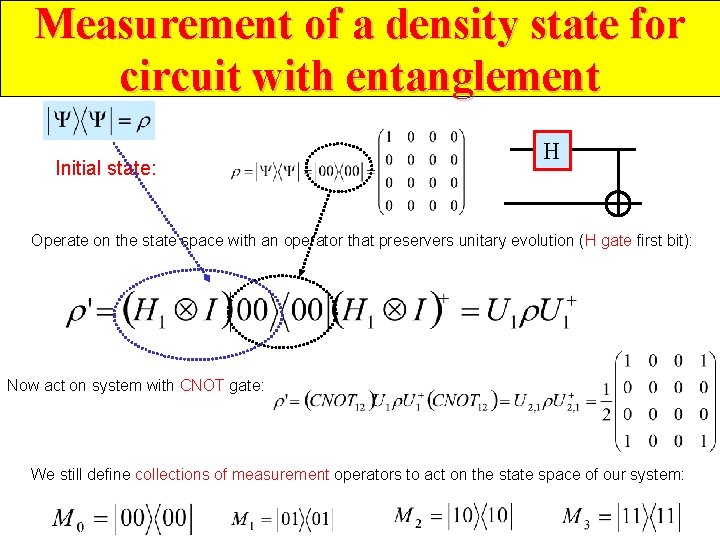
Measurement of a density state for circuit with entanglement Initial state: H Operate on the state space with an operator that preservers unitary evolution (H gate first bit): Now act on system with CNOT gate: We still define collections of measurement operators to act on the state space of our system:

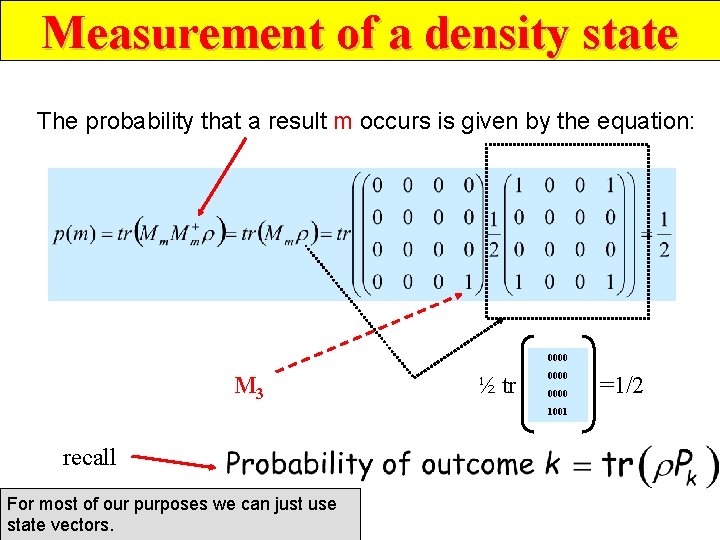
Measurement of a density state The probability that a result m occurs is given by the equation: 0000 M 3 ½ tr 0000 1001 recall For most of our purposes we can just use state vectors. =1/2

REMINDER: Ensemble point of view Probability of outcome k being in state j Formula linking trace and density matrix Probability of being in state j

REMINDER: Ensemble point of view Probability of outcome k being in state j Probability of being in state j

Postulate 3: Quantum Measurement Now we can formulate precisely the Postulate 3

Now we use this notation for an Example of Qubit Measurement [ 0* 1*] 1 0 00 10 00 0 1 0 = [ 0* 1*] 10 00 1 We show here two methods to derive it. Check for homeworks and exam

How the state vector changes in measurement? M 0 | > = = |0> (<0| 0 |0> + <0| 1 |1> = |0> 0

What happens to a system after a Measurement? • After a system or subsystem is measured from outside, its state appears to collapse to exactly match the measured outcome – the amplitudes of all states perfectly distinguishable from states consistent with that outcome drop to zero – states consistent with measured outcome can be considered “renormalized” so their probabilities sum to 1 Only orthogonal state can be distinguished in a measurement

Projective Measurements: Average Values and Standard Deviations Observable: Can write: Average value of a measurement: scalar Standard deviation of a measurement: scalar

Phase Global phase Relative phase can be physically distinquished Relative phase depends on the basis

Postulate 4: Composite Systems

Compound Systems • Let C=AB be a system composed of two separate subsystems A, B each with vector spaces A, B with bases |ai , |bj. • The state space of C is a vector space C=A B given by the tensor product of spaces A and B, with basis states labeled as |aibj.

Composition example The state space of a composite physical system is the tensor product of the state spaces of the components – n qubits represented by a 2 n-dimensional Hilbert space – composite state is | = | 1 | 2 . . . | n – e. g. 2 qubits: | 1 = 1|0 + 1|1 | 2 = 2|0 + 2|1 | = | 1 | 2 = 1 2|00 + 1 2|01 + 1 2|10 + 1 2|11 – entanglement 2 qubits are entangled if | | 1 | 2 for any | 1 , | 2 e. g. | = |00 + |11

Entanglement • If the state of compound system C can be expressed as a tensor product of states of two independent subsystems A and B, Entanglement results from c = a b, axioms/postulates. It exists only for quantum states • then, we say that A and B are not entangled, and they have individual states. – E. g. |00 +|01 +|10 +|11 =(|0 +|1 ) • Otherwise, A and B are entangled (basically correlated); their states are not independent. – E. g. |00 +|11

Size of Compound State Spaces • Note that a system composed of many separate subsystems has a very large state space. • Say it is composed of N subsystems, each with k basis states: – The compound system has k. N basis states! – There are states of the compound system having nonzero amplitude in all these k. N basis states! – In such states, all the distinguishable basis states are (simultaneously) possible outcomes (each with some corresponding probability) – Illustrates the “many worlds” nature of quantum mechanics.

Postulate 4: Composite Systems

Summary on Postulates Hilbert Space Evolution Measurement Tensor Product

Key Points to Remember: • An abstractly-specified system may have many possible states; only some are distinguishable. • A quantum state/vector/wavefunction assigns a complex-valued amplitude (si) to each distinguishable state si (out of some basis set) • The probability of state si is | (si)|2, the square of (si)’s length in the complex plane. • States evolve over time via unitary (invertible, length-preserving) transformations. • Statistical mixtures of states are represented by weighted sums of density matrices =| |.

Key points to remember • • The Schrödinger Equation The Hamiltonian The Evolution Matrix How complicated is a single Quantum Bit? Measurement operators Measurement of a state vector using projective measurement • Density Matrix and the Trace • Ensembles of quantum states, basic definitions and importance • Measurement of a density state

Bibliography & acknowledgements • Michael A. Nielsen and Isaac L. Chuang, Quantum Computation and Quantum Information, Cambridge University Press, Cambridge, UK, 2002 • V. Bulitko, On quantum Computing and AI, Notes for a graduate class, University of Alberta, 2002 • R. Mann, M. Mosca, Introduction to Quantum Computation, Lecture series, Univ. Waterloo, 2000 http: //cacr. math. uwaterloo. ca/~mmosca/quantumcou rsef 00. htm D. Fotin, Introduction to “Quantum Computing Summer School”, University of Alberta, 2002.

Additional Slides

Distinguishability Recall that M is measurement operator We represent | 2 in new base On the other hand Thus we have contradiction, states can be distinguished unless they are orthogonal

General Measurements in compound spaces

Uncertainty Principle

Positive Operator-Valued Measurements (POVM)

• This lecture was taught in 2005, 2007 • There is more about trace and partial trace in future lectures and examples.