Chap 4 Quantum Mechanics In Three Dimensions 1

Chap 4. Quantum Mechanics In Three Dimensions 1. Schrodinger Equation in Spherical Coordinates 2. The Hydrogen Atom 3. Angular Momentum 4. Spin

4. 1. Schrodinger Equation in Spherical Coordinates 1. Separation of Variables 2. The Angular Equation 3. The Radial Equation Read Prob 4. 1

Orthogonal Curvilinear Coordinates Ref: G. Arfken, “Mathematical Methods for Physicists”, 3 rd ed. , Chap. 2. B. Schutz, “Geometrical Methods of Mathematical Physics”, p. 148. Spherical coordinates :

4. 1. 1. Separation of Variables V V(r) Spherical coordinates : Ansatz :

Set dimensionless constant Or

Mnemonics Do Prob 4. 2

4. 1. 2. The Angular Equation Ansatz : Set

Azimuthal Solutions single-valued, i. e. ,

Legendre Polynomials Setting m 0 gives Frobenius method shows that convergence requires See Arfken (3 rd ed) Ex 8. 5. 5 The corresponding solutions are called the Legendre polynomials, which can also be defined by the Rodrigues formula :

1 st few Legendre Polynomials Normalization: Pl (1) = 1

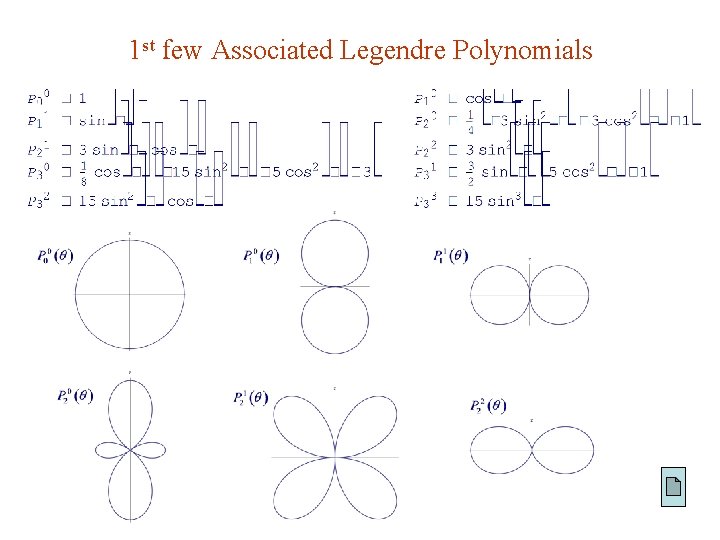
Associated Legendre Functions Solutions to the m 0 case : are called associated Legendre functions defined by Griffiths: where Arfken, Mathenmatica: Thus while m takes on 2 l + 1 values : Note : Another independent solution exists but is not physically acceptable ( see Prob. 4. 4 ).

1 st few Associated Legendre Polynomials

Normalization Spherical Harmonics Normalization : Griffiths : Arfken, Mathenmatica: Note : Orthonormality : where

1 st few Spherical Harmonics Do Prob 4. 3 Read Prob 4. 4, 4. 6

4. 1. 3. The Radial Equation Set Effective potential Normalization : Centrifugal term

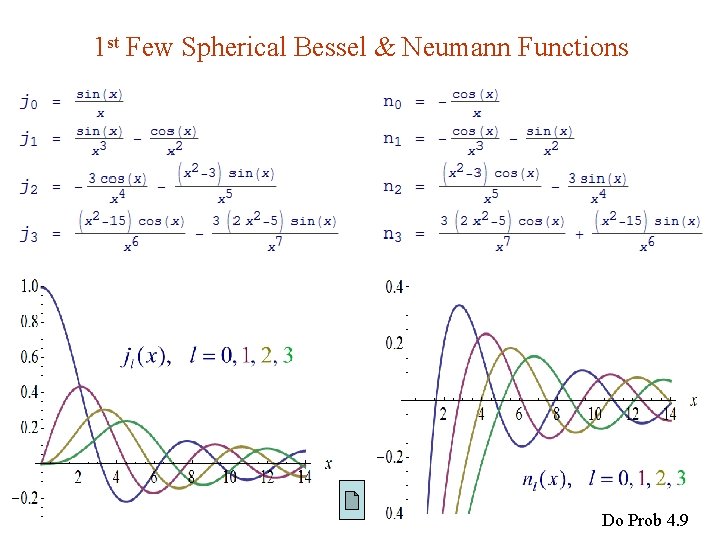
Example 4. 1. Infinite Spherical Well Let Find the wave functions and the allowed energies. Ans : jl = spherical Bessel function nl = spherical Neumann function

Spherical Bessel & Neumann Functions nl (0) jl (0) is finite Let n l be the nth zero of jl. (2 l+1)-fold degeneracy in m.

1 st Few Spherical Bessel & Neumann Functions Do Prob 4. 9

Bessel & Neumann Functions The Bessel & Neumann functions are solutions to the radial part of the Helmholtz equation in cylindrical coordinates : Bessel Modified Bessel functions Neumann functions ( for 2 < 0 )

Spherical Bessel & Neumann Functions The spherical Bessel & Neumann functions are solutions to the radial part of the Helmholtz equation in spherical coordinates : Spherical Bessel Neumann functions

Asymptotic Forms for x 0 for x

4. 2. The Hydrogen Atom 1. The Radial Wave Function 2. The Spectrum of Hydrogen

Bohr’s Model Circular orbit : Quantization of angular momentum : Bohr radius

4. 2. 1. The Radial Wave Function Bound States ( E < 0 ) : Set

Asymptotic Behavior : u finite everywhere 0: u finite everywhere Set

Factor-Out Asympototic Behavior

Frobenius Method

Series Termination j : Series must terminate : ( unacceptable for large )

Eigenenergies Let = principal quantum number n 1, 2, 3, . . . Bohr radius :

Eigenfunctions Eigenfunction belonging to eigenenergy is where with

n 1, l 0. Normalization : Ground State

n 2, l 0, 1. 1 st Excited States m 1, 0, 1 Normalization : see Prob. 4. 11 Degeneracy of nth excited state :

Associated Laguerre Polynomials qth Laguerre polynomial ; Used by Griffiths. Used by Arfken & Mathematica. 1/n! of Griffiths’ value. Associated Laguerre polynomial Used by Arfken & Mathematica. 1/(n+p)! Griffiths’ value. Differential eqs. :

1 st Few Laguerre & Associated Laguerre. Polynomials Ln : Arfken & Mathematica convention Griffiths’ / n! Lna : Arfken & Mathematica convention Griffiths’ / (n+a)!

Orthogonal Polynomials Ref: M. Abramowitz, I. A. Stegun, “Handbook of Mathematical Functions”, Chap 22. w weight function Orthogonality: Differential eq. : Recurrence relations: Rodrigues’ formula: fn (a, b) en w g Standard An Pn ( 1, 1) ( )n n! 2 n 1 x 2 1 Pn(1) = 1 2 / (2 n+1) Ln ( 0, ) 1 e x x 1 Ln p ( 0, ) ( )p e x xp x (p+n)! / n! Hn ( , ) ( )n exp( x 2/2) 1 en = ( 1)n n! 2

Hydrogen Wave Functions Griffiths convention Arfken convention : [3 rd ed. , eq(13. 60)] Orthonormality : Arfken

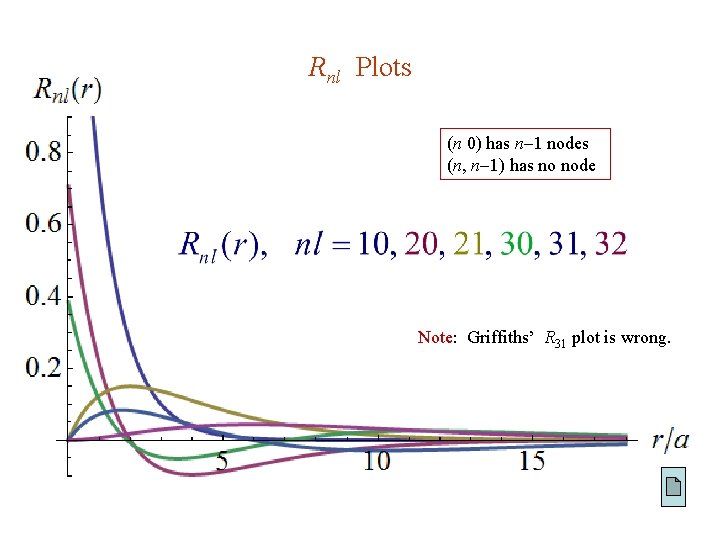
First Few Rnl (r)

Rnl Plots (n 0) has n 1 nodes (n, n 1) has no node Note: Griffiths’ R 31 plot is wrong.

Density Plots of 4 l 0 White = Off-scale (400) (410) (n 0 m) has n 1 nodes (n, n 1, m) has no node (420) (430) White = Off-scale

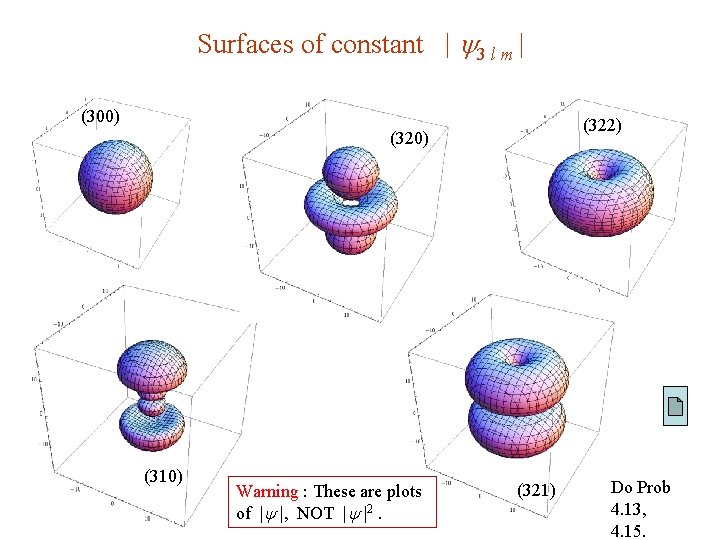
Surfaces of constant | 3 l m | (300) (322) (320) (310) Warning : These are plots of | |, NOT | |2. (321) Do Prob 4. 13, 4. 15.

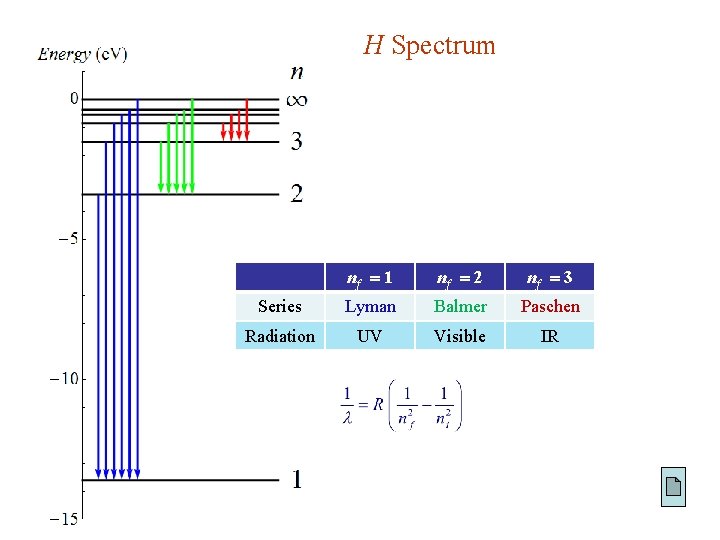
4. 2. 2. The Spectrum of Hydrogen H under perturbation transition between “stationary” levels: energy absorbed : to higher excited state energy released : to lower state H emitting light ( Ei > Ef ) : Planck’s formula : where Rydberg formula Rydberg constant

H Spectrum nf 1 nf 2 nf 3 Series Lyman Balmer Paschen Radiation UV Visible IR

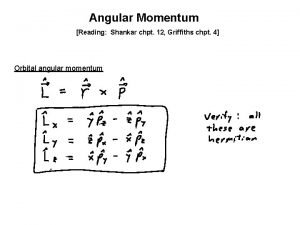
4. 3. Angular Momentum CM : QM : 1. Eigenvalues 2. Eigenfunctions

Commutator Manipulation Similarly distributive

[ Li , Lj ] Cyclic permutation :

Uncertainty Principle Only one component of L is determinate.

[ L 2, L ] Similarly i. e. L 2 & Lz share the same eigenfunction : for i x, y, z

4. 3. 1. Eigenvalues Ladder operators : Let L f is an eigenfunction of L 2. L f is an eigenfunction of Lz. L raiseslowers eigenvalue of Lz by .

Lz finite max( ). Let Also Now Lz finite min( ). Let Also

Since N = integer Let where or max must be integer or half integer

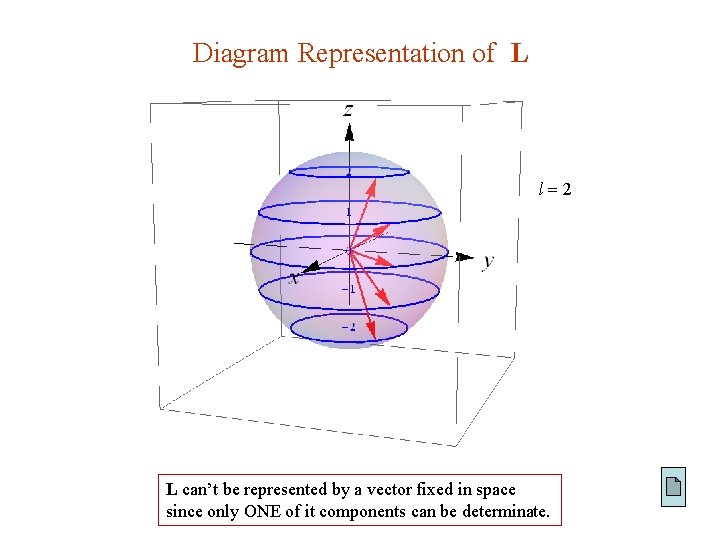
Diagram Representation of L l 2 L can’t be represented by a vector fixed in space since only ONE of it components can be determinate.

4. 3. 2. Eigenfunctions Gradient in spherical coordinates :

Do Prob. 4. 21 Read Prob 4. 18, 4. 19, 4. 20 Do Prob 4. 24

4. 4. Spin 1/2 2. Electrons in a Magnetic Field 3. Addition of Angular Momenta

Spin is an intrinsic angular momentum satisfying with

4. 4. 1. Spin 1/2 2 -D state space spanned by (spin down ) (spin up ) In matrix form (spinors) : General state : Operators are 2 2 matrices.

Pauli Matrices Pauli matrices

Spin Measurements with Let particle be in normalized state : Measuring Sz then has a probability | a |2 of getting /2, and probability | b |2 of getting /2, Characteristic equation is Eigenvalues : Eigenvectors :

Writing in terms of (x) : Measuring Sx then has a probability | |2 of getting /2, and probability | |2 of getting /2, Read last paragraph on p. 176. Do Prob 4. 26, 27 Read Prob 4. 30

4. 4. 2. Electrons in a Magnetic Field Ampere’s law : Current loop magnetic moment . Likewise charge particle with angular momentum. gyromagnetic ratio QM : Spin is an angular momentum : experiences a torque when placed in a magnetic field B : tends to align with B, i. e. , // B is the ground state with 0 QM : L has no fixed direction can’t be aligned to B Larmor precession

Example 4. 3. Larmor Precession Consider a spin ½ particle at rest in uniform The Hamiltonian is H + E+ B 0 / 2 E + B 0 / 2 Sz /2 / 2 H & S share the same eigenstates : Time evolution of is

Sinilarly if a, b are real

Set i. e. , S is tilted a constant angle from the z-axis, and precesses with the Larmor frequency ( same as the classical law )

Example 4. 4. The Stern-Gerlach Experiment Force on in inhomogeneous B : Consider a particle moving in the y-direction in a field Note : The x term is to make sure Due to precession about B 0 , Sx oscillates rapidly & averages to zero. Net force is incident beam splits into two. In contrast, CM expects a continuous spread-out.

Alternative Description In frame moving with particle : x component dropped for convenience for t 0 Let for 0 t T where for t > T

for t > T spin up particles move upward spin up particles move downward S-G apparatus can be used to prepare particles in particular spin state.

4. 4. 3. Addition of Angular Momenta The angular momentum of a system in state can be found by writing where is proportional to the probability of measuring If the system has two types of angular momenta j 1 and j 2 , its state can be written as where The total angular momentum of the system is therefore described by the quantities

Since either set of basis is complete, we have The transformation coefficients are called Clebsch-Gordan coeffiecients (CGCs). The problem is equivalent to writing the direct product space as a direct sum of irreducible spaces

4. 4. 3. Addition of Angular Momenta Rules for adding two angular momenta : State j 1 j 2 J 1 J 2. . . Jn | j 1 m 1 | j 2 m 2 | J 1 M 1 . . . | Jn Mn 1. Possible values of S are j 1 + j 2 , j 1 + j 2 1, . . . , | j 1 j 2 | + 1, | j 1 j 2 | 2. Only states with M = m 1 + m 2 are related. 3. Linear transformation between | j 1 m 1 | j 2 m 2 and | Jk Mk can be obtained by applying the lowering operator to the relation between the “top” states. 4. Coefficients of these linear transformation are called the Clebsch-Gordan ( CG ) coefficients.

Example: Two Spin ½ Particles s 1 = ½ , s 2 = ½ s 1 s 2 = 0 s 1 + s 2 = 1, Possible total S 1, 0 States s 1 s 2 | | | S 1 S 2 |11 |10 | 1 1 |00

“Top” state for S = 1 : “Top” state for S = 0 : Normalization then gives must be orthogonal to | 10 .

J 1 J 2 M = m 1 + m 2 m 1 , m 2 M . . .

Clebsch-Gordan ( C-G ) coefficients Shaded column gives Shaded row gives Sum of the squares of each row or column is 1. Do Prob 4. 36