Quantum Transport Outline l What is Computational Electronics

Quantum Transport

Outline: l What is Computational Electronics? l Semi-Classical Transport Theory ¡ Drift-Diffusion Simulations ¡ Hydrodynamic Simulations ¡ Particle-Based Device Simulations l Inclusion of Tunneling and Size-Quantization Effects in Semi-Classical Simulators ¡ Tunneling Effect: WKB Approximation and Transfer Matrix Approach ¡ Quantum-Mechanical Size Quantization Effect l Drift-Diffusion and Hydrodynamics: Quantum Correction and Quantum Moment Methods l Particle-Based Device Simulations: Effective Potential Approach l Quantum Transport ¡ Direct Solution of the Schrodinger Equation (Usuki Method) and Theoretical Basis of the Green’s Functions Approach (NEGF) ¡ NEGF: Recursive Green’s Function Technique and CBR Approach ¡ Atomistic Simulations – The Future l Prologue

Quantum Transport ¡ Direct Solution of the Schrodinger Equation: Usuki Method (equivalent to Recursive Green’s Functions Approach in the ballistic limit) ¡ NEGF (Scattering): Recursive Green’s Function Technique, and l CBR approach l ¡ Atomistic Devices Simulations – The Future of Nano

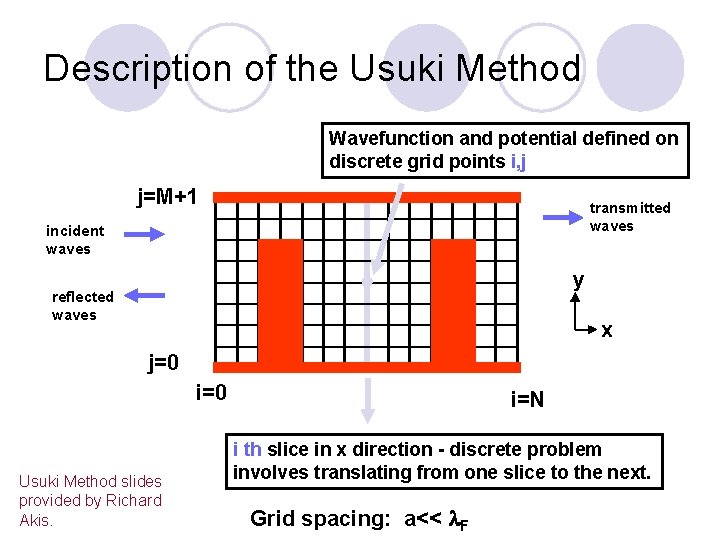
Description of the Usuki Method Wavefunction and potential defined on discrete grid points i, j j=M+1 transmitted waves incident waves y reflected waves x j=0 i=0 Usuki Method slides provided by Richard Akis. i=N i th slice in x direction - discrete problem involves translating from one slice to the next. Grid spacing: a<< l. F

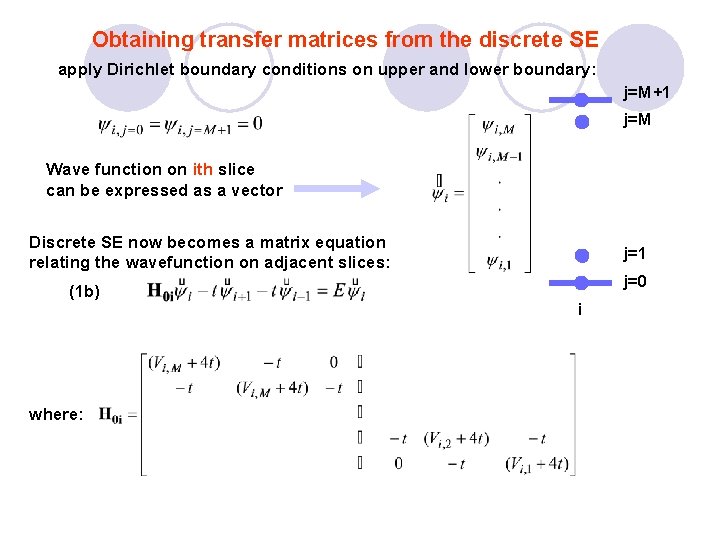
Obtaining transfer matrices from the discrete SE apply Dirichlet boundary conditions on upper and lower boundary: j=M+1 j=M Wave function on ith slice can be expressed as a vector Discrete SE now becomes a matrix equation relating the wavefunction on adjacent slices: (1 b) where: j=1 j=0 i

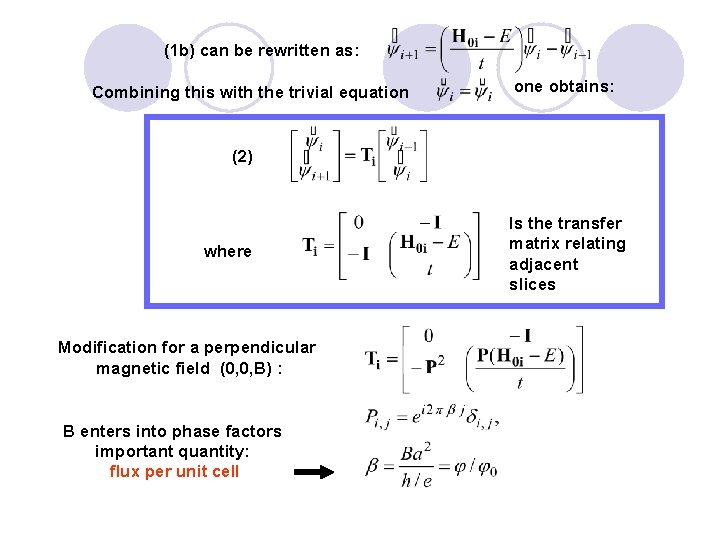
(1 b) can be rewritten as: Combining this with the trivial equation one obtains: (2) where Modification for a perpendicular magnetic field (0, 0, B) : B enters into phase factors important quantity: flux per unit cell Is the transfer matrix relating adjacent slices

yields the modes on the left side of the system Solving the eigenvalue problem: Mode eigenvectors have the generic form: redundant There will be M modes that propagates to the right (+) with eigenvalues: propagating evanescent There will be M modes that propagates to the left (+) with eigenvalues: propagating evanescent defining Complete matrix of eigenvectors: and

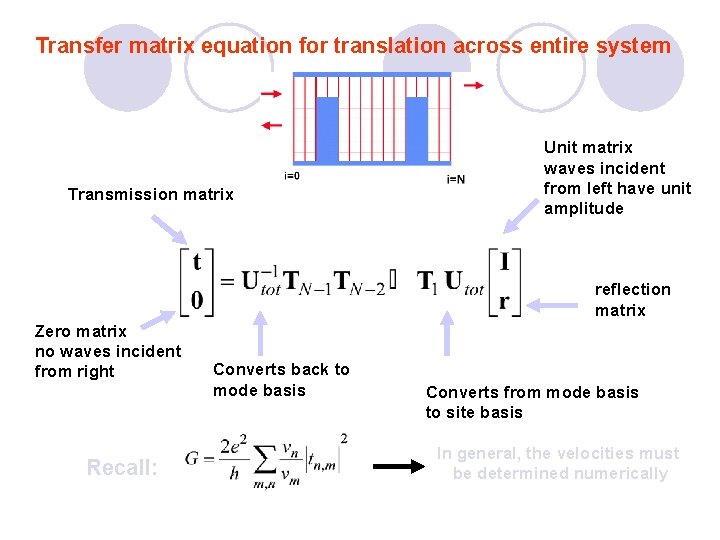
Transfer matrix equation for translation across entire system Transmission matrix Unit matrix waves incident from left have unit amplitude reflection matrix Zero matrix no waves incident from right Recall: Converts back to mode basis Converts from mode basis to site basis In general, the velocities must be determined numerically

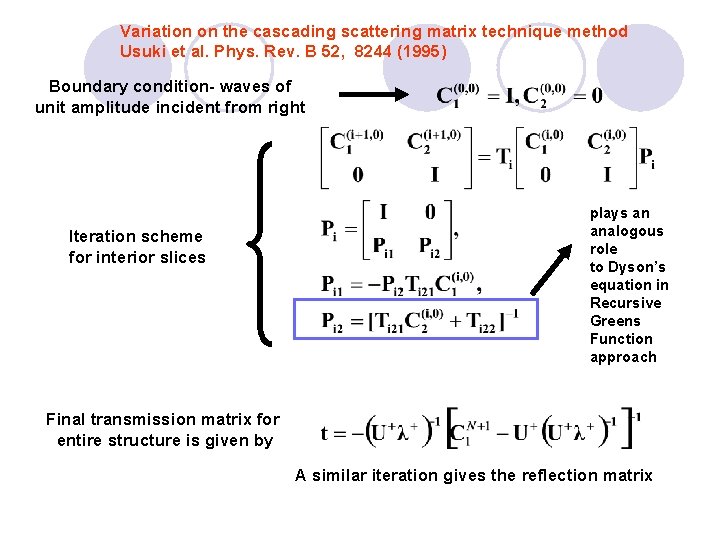
Variation on the cascading scattering matrix technique method Usuki et al. Phys. Rev. B 52, 8244 (1995) Boundary condition- waves of unit amplitude incident from right Iteration scheme for interior slices plays an analogous role to Dyson’s equation in Recursive Greens Function approach Final transmission matrix for entire structure is given by A similar iteration gives the reflection matrix

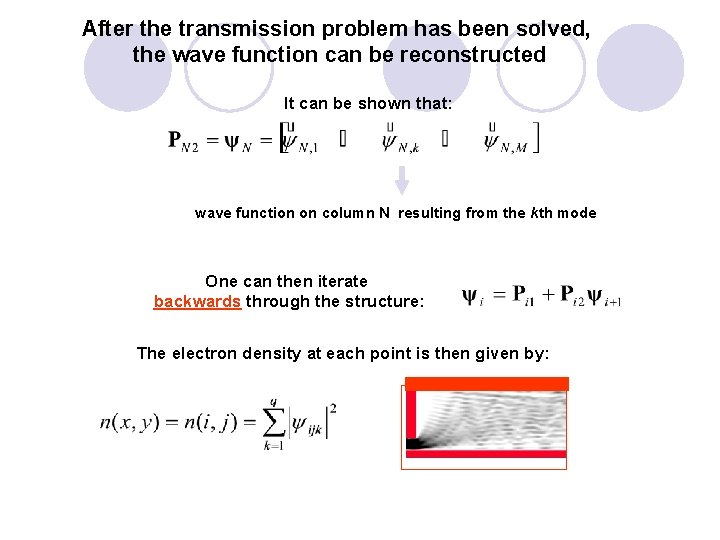
After the transmission problem has been solved, the wave function can be reconstructed It can be shown that: wave function on column N resulting from the kth mode One can then iterate backwards through the structure: The electron density at each point is then given by:

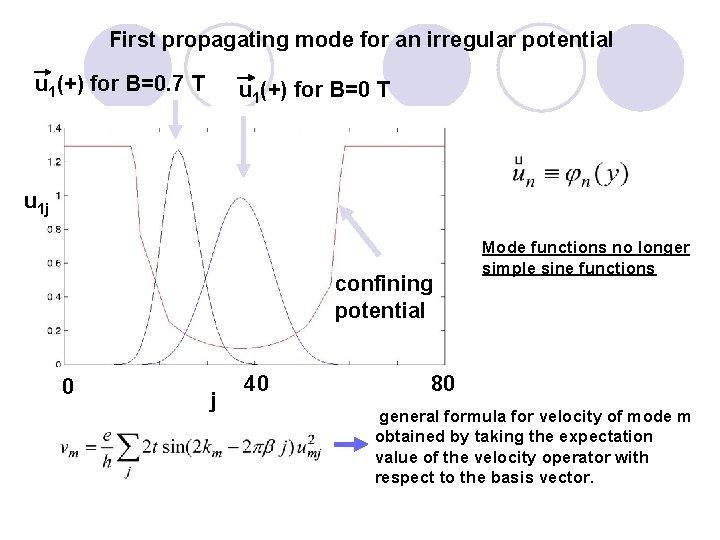
First propagating mode for an irregular potential u 1(+) for B=0. 7 T u 1(+) for B=0 T u 1 j confining potential 0 j 40 Mode functions no longer simple sine functions 80 general formula for velocity of mode m obtained by taking the expectation value of the velocity operator with respect to the basis vector.

Conduction band [e. V] Example – Quantum Dot Conductance as a Function of Gate voltage 0. 8 Simulation gives comparable 2 D electron density to that measured experimentally Conduction band profile Ec 0. 6 Energy of the ground subband 0. 4 0. 2 0. 0 Fermi level EF -0. 2 0. 00 0. 02 0. 04 0. 06 0. 08 0. 10 z-axis [mm] Potential felt by 2 DEG- maximum of electron distribution ~7 nm below interface Vg= -1. 0 V Vg= -0. 9 V Vg= -0. 7 V Potential evolves smoothly- calculate a few as a function of V g, and create the rest by interpolation

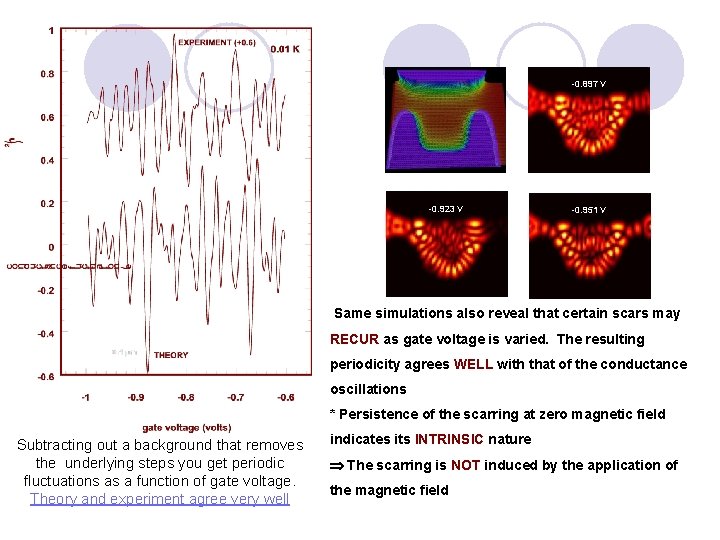
-0. 897 V -0. 923 V -0. 951 V Same simulations also reveal that certain scars may RECUR as gate voltage is varied. The resulting periodicity agrees WELL with that of the conductance oscillations * Persistence of the scarring at zero magnetic field Subtracting out a background that removes the underlying steps you get periodic fluctuations as a function of gate voltage. Theory and experiment agree very well indicates its INTRINSIC nature The scarring is NOT induced by the application of the magnetic field

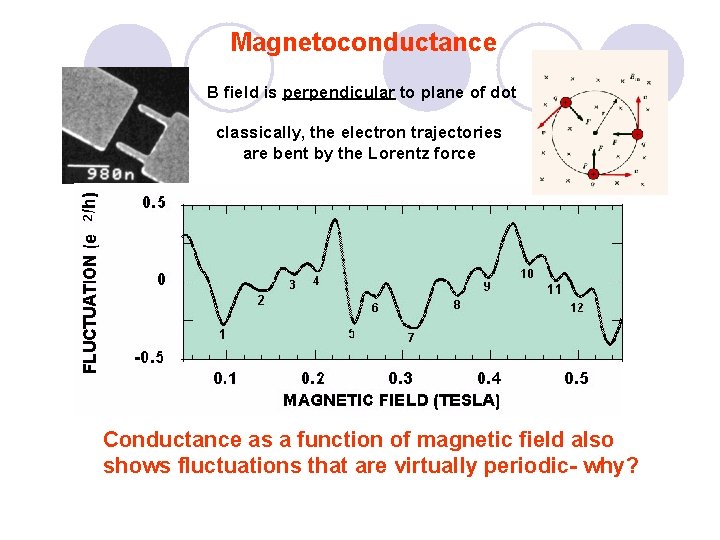
Magnetoconductance B field is perpendicular to plane of dot classically, the electron trajectories are bent by the Lorentz force Conductance as a function of magnetic field also shows fluctuations that are virtually periodic- why?

Green’s Function Approach: Fundamentals l l l The Non-Equilibrium Green’s function approach for device modeling is due to Keldysh, Kadanoff and Baym It is a formalism that uses second quantization and a concept of Field Operators It is best described in the so-called interaction representation In the calculation of the self-energies (where the scattering comes into the picture) it uses the concept of the partial summation method according to which dominant self-energy terms are accounted for up to infinite order For the generation of the perturbation series of the time evolution operator it utilizes Wick’s theorem and the concepts of time ordered operators, normal ordered operators and contractions

Relevant Literature l l l A Guide to Feynman Diagrams in the Many-Body Problem, 2 nd Ed. R. D. Mattuck, Dover (1992). Quantum Theory of Many-Particle Systems, A. L. Fetter and J. D. Walecka, Dover (2003). Many-Body Theory of Solids: An Introduction, J. C. Inkson, Plenum Press (1984). Green’s Functions and Condensed Matter, G. Rickaysen, Academic Press (1991). Many-Body Theory G. D. Mahan (2007, third edition). L. V. Keldysh, Sov. Phys. JETP (1962).

Schrödinger, Heisenberg and Interaction Representation l Schrödinger picture l Interaction picture l Heisenberg picture

Time Evolution Operator Time evolution operator representation as a time-ordered product

Contractions and Normal Ordered Products

Wick’s Theorem l Contraction (contracted product) of operators For more operators (F 83) all possible pairwise contractions of operators l Uncontracted, all singly contracted, all doubly contracted, … l l Take matrix element over Fermi vacuum l All terms zero except fully contracted products

Propagator

Partial Summation Method

Example: Ground State Calculation

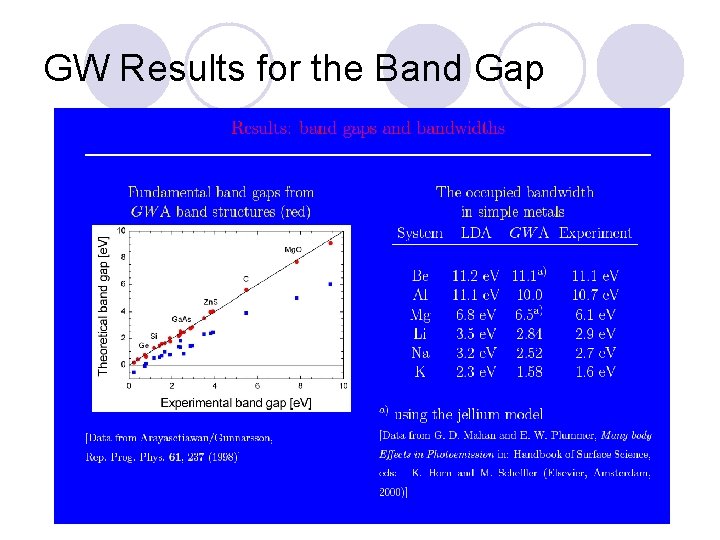
GW Results for the Band Gap

Definitions of Green’s Functions * 1 = x 1, t 1 Time ordered Allows perturbation theory (Wick’s theorem) Retarded, Advanced Simple analitycal structure and spectral analysis Correlation functions Direct access to observable expectation values

Equilibrium Properties of the System Gr, Ga, G<, G> are enough to evaluate all the GF’s and are connected by physical relations General identities Fluctuation-dissipation th. Spectral function Ø Just one indipendent GF See eg: H. Haug, A. -P. Jauho A. L. Fetter, J. D. Walecka

Non-Equilibrium Green’s Functions See eg: D. Ferry, S. M. Goodnick H. Haug, A. -P. Jauho J. Hammer, H. Smith, RMP (1986) G. Stefanucci, C. -O. Almbladh, PRB (2004) • Time dep. phenomena • Electric fields • Coupling to contacts at different chemical potentials Ø Contour-ordered perturbation theory: Gr, Ga, G<, G> are all involved in the PT 2 of them are indipendent No fluctuation dissipation theorem Contour ordering

Constitutive Equations Ø Two Equations of Motion In the time-indipendent limit Dyson Equation Keldysh Equation Gr, G< coupled via the self-energies Computing the (coupled) Gr, G< functions allows for the evaluation of transport properties

Summary This section first outlined the Usuki method as a direct way of solving the Schrodinger equation in real space l In subsequent slides the Green’s function approach was outlined with emphasis on the partial summation method and the self-energy calculation and what are the appropriate Green’s functions to be solved for in equilibrium, near equilibrium (linear response) and high-field transport conditions l