O M Mhendislik Fakltesi evre Mhendislii Blm BTNLEM

O. M. Ü Mühendislik Fakültesi Çevre Mühendisliği Bölümü BÜTÜNLEŞMİŞ EKOSİSTEM MODELLERİ Prof. Dr. Gülfem BAKAN 1

KÜTLE DENGESİ, KARARLI HAL ÇÖZÜMÜ ve TEPKİ SÜRESİ 2

• Kütle Dengesi • Kararlı hal çözümü • Transfer fonksiyonu (hidrolik çevrim) ve alıkonma süreleri • Benzer sistemlerin zamanla ilgili özelliklerinin ölçümü için tepki süresi hesabı ve • Kütle denkliği modelinin zaman değişimli genel çözümü 3

• Su hacmi ne kadar gelişecek? • Bu gelişimin oluşması ne kadar sürecek? 4

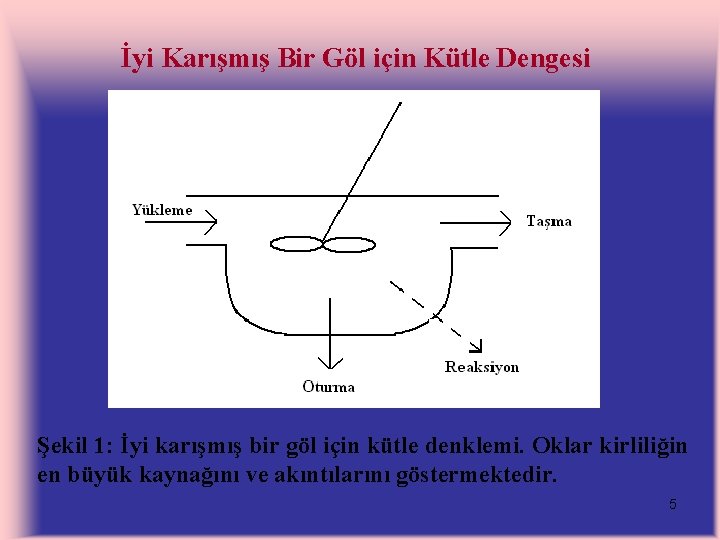
İyi Karışmış Bir Göl için Kütle Dengesi Şekil 1: İyi karışmış bir göl için kütle denklemi. Oklar kirliliğin en büyük kaynağını ve akıntılarını göstermektedir. 5

Sonlu bir zaman periyodu için sistemin kütle denkliği şu şekilde açıklanabilir: Birikim=Yükleme–Taşma–Tepkime–Çökelme (1) Böylece sistemde yüklemeye katkıda bulunan tek bir kaynak ve sistemden ayrılan üç akıntı (taşma, tepkime, çökelme) vardır. 6

Birikim: Birikim t zaman boyunca M kütlesinin değişimini gösterir. (2) Kütle konsantrasyona bağlıdır. (3) V, sistemin hacmidir (L 3). (3) denklemi M=V. C (4) haline dönüştürülerek Eşitlik 2 de yerine konursa; (5) 7

V Sabit (6) Δt çok küçük (7) Böylece konsantrasyon zamanla arttıkça kütle birikir (d. C/dt pozitif) ve konsantrasyon zamanla azaldıkça kütle azalır (d. C/dt negatif). Kararlı hal durumunda kütle sabittir(d. C/dt =0). Birikimin birimi zamana göre kütledir (M. T-1). 8

Yükleme: Kütle değişik kaynaklardan ve farklı yollardan göle gelir. • İşletme tesislerinin çıkış suları • Akarsu kolları tarafından taşınan kütle Yükleme=W(t) (8) W(t): kütle yükleme oranı (M. T-1) ve t yüklemenin zamanın bir fonksiyonu olduğunu gösterir. 9

(9) Q= Sisteme giren tüm su kaynaklarının hacimsel oranı (L 3 T-1) ve Cin(t)=bu kaynakların ortalama giriş konsantrasyonu (M. L-3). Farz ediyoruz ki; • Akış sabittir • Yüklemedeki geçici değişikliklerin tümü akış konsantrasyonundaki geçici değişimlerin sonucudur. 10

Ayrıca ortalama akış konsantrasyonu 8 ve 9 eşitliğindeki yükleme ilişkilendirilebilir. (10) Dışa akış: Şekildeki basit sistemimizde kütle bir akarsu tarafından sistemden taşınır. Cout=C Dışa akış= Q. C (11) 11

Reaksiyon: Her ne kadar doğal sulardan kirleticileri söken reaksiyonları formüle etmek için birçok yol olsa da açıkça en yaygın olan birinci derece gösterim; Reaksiyon=k. M (12) k= ilk temel reaksiyon katsayısı (T-1). Böylece, lineer orantılılık kirliliğin arındırılması ve mevcut kirlilik kütlesi arasındaki oran olarak kabul edilir. Eşitlik (12) konsantrasyon cinsinden şöyle ifade edilir: Reaksiyon=k. V. C (13) 12

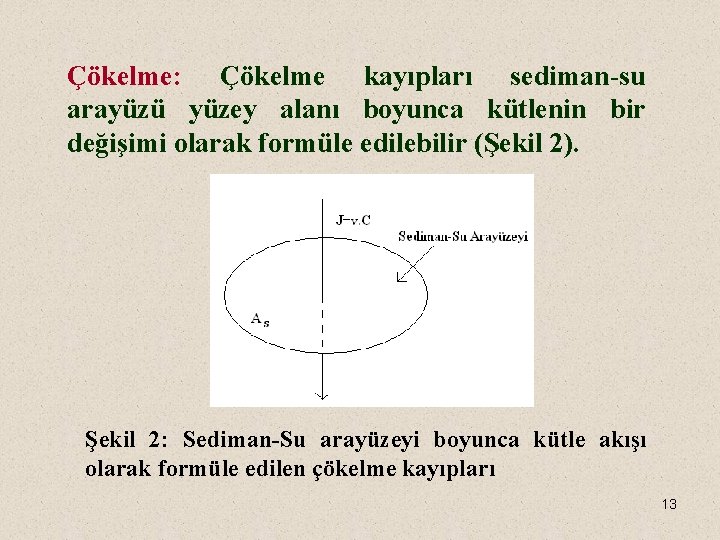
Çökelme: Çökelme kayıpları sediman-su arayüzü yüzey alanı boyunca kütlenin bir değişimi olarak formüle edilebilir (Şekil 2). Şekil 2: Sediman-Su arayüzeyi boyunca kütle akışı olarak formüle edilen çökelme kayıpları 13

Böylece akışı konsantrasyonla çarparak kütle dengesindeki çökelme terimi şu şekilde geliştirilebilir; Çökelme= v. As. C (14) Burada; v=görünen çökelme hızı (L. T-1) As=Sedimanların yüzey alanı (L 2). Çökelme hızı “görünen” olarak adlandırılır çünkü göl sedimanlarına kirletici taşıyan farklı proseslerin net etkilerini ifade etmektedir. Örneğin kirleticilerin bazıları çözünmüş formda olabilir ve bu nedenle çökelmeye maruz kalmaz. Böyle durumlar için “gerçek” çökelme hızı bu mekanizmanın net etkisini göstermek için 14 kullanılmayabilir.

Eşitlik (14) ayrıca birinci reaksiyona benzer biçimde formüle edilebilir; Çökelme=ks. V. C (15) Burada; ks=ilk çökelme oranı sabiti=v/H. v/H oranı reaksiyon oranı k ile aynı birimlere sahiptir (T-1). Bu gösterimin geçerliliği göl yüzeyi alanı ve sediman alanının eşit olduğu kabulüyle mümkündür. 15

Toplam Denge: Terimler çok iyi karışmış bir göl için aşağıdaki kütle dengesinde birleştirilebilir: (16) Konsantrasyon C ve zaman t sırasıyla bağımlı ve bağımsız değişkenlerdir, çünkü model zamanın bir fonksiyonu olarak konsantrasyonu tahmin etmek için boyutlandırılır. 16

Kararlı Hal Çözümleri Sistem eğer yeterli bir zaman için sabit bir yüklemeye bağlı ise, kararlı hal olarak adlandırılan dinamik denge durumuna ulaşacaktır. Matematiksel terimlerde bu şu anlama gelir ki birikim sıfırdır (d. C/dt=0). Bu durum için Eşitlik (16) şu şekilde çözülebilir: (17) veya (18) formatını kullanarak 17

(18) Asimilasyon çarpanı a = Q+k. V+v. As (19) Örnek 1: Kütle Dengesi Göl aşağıdaki özelliklere sahiptir; Hacim: 50000 m 3 Ortalama derinlik: 2 m Giren akış = Çıkan akış = 7500 m 3 d-1 Sıcaklık: 25 0 C Göl üç kaynaktan kirlilik girdisi almaktadır; 50 kg. g-1 fabrika deşarjı, atmosferden 0. 6 g. m-2. g-1’lik akış ve 10 mg. L-1’lik konsantrasyonda giren ırmak. 18

Eğer kirlilik 20 0 C de 0. 25 d-1 de çürürse (θ=1. 05) a)Özümleme çarpanı b)Kararlı hal konsantrasyonunu belirleyin c)Kütle dengesindeki her terim için kütle/zamanı hesapla ve sonuçları bir çizimle göster. Çözüm: a)Çürüme oranı sıcaklığa göre düzeltilmelidir. k=0. 25*1. 0525 -20=0. 319 d-1 (0. 319/gün) Sonra özümleme çarpanı şu şekilde hesaplanabilir: 19

a = Q+k. V= 7500+0. 319. (50000)=23454 m 3 d-1 b) Gölün yüzey alanı hesaplamak için gereklidir. atmosferik yüklemeyi Atmosferik yükleme şöyle hesaplanır; İçeri akan ırmak yükü şöyle hesaplanabilir; 20

Bu yüzden toplam yükleme; ve konsantrasyon şöyle belirlenebilir (Eşitlik 18) c)Çıkış boyunca sürüklenme kaybı şöyle hesaplanabilir; 21

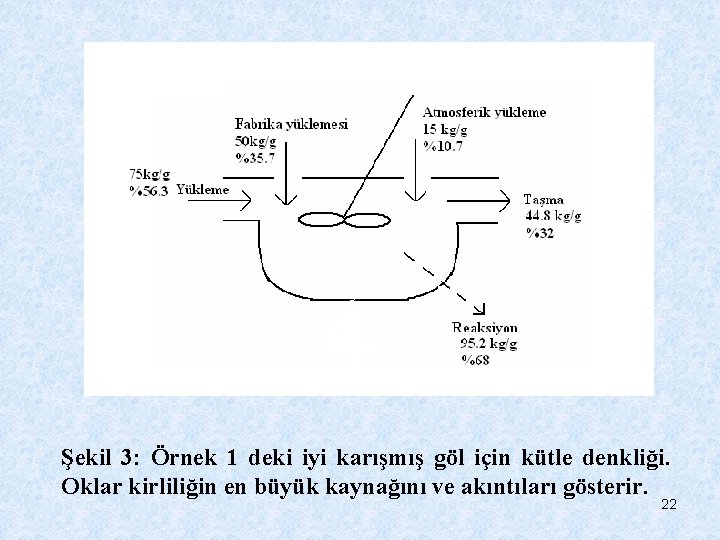
Şekil 3: Örnek 1 deki iyi karışmış göl için kütle denkliği. Oklar kirliliğin en büyük kaynağını ve akıntıları gösterir. 22

Transfer(Dönüşüm) Fonksiyonları ve Alıkonma Zamanı Transfer Fonksiyonu: Eşitlik 17 yi formüle etmek için bir diğer yol, Eşitlik 9 biçiminde yüklemeyi ifade etmeye dayanır. Kararlı hal durumu için, (20) Eşitlik (17) ye konursa ve her iki pay ve payda Cin e bölünürse; (21) β transfer (taşınım) fonksiyonudur. 23

(22) Eşitlik (22) “transfer fonksiyonu” olarak adlandırılır çünkü sistem girdisinin (Cin olarak gösterilen) nasıl çıktıya (C olarak gösterilen) dönüştürüldüğü veya “transfer edildiği” ni belirtir. Eğer β<<1 ise, gölün hareket(sökme) mekanizması gölde kirlilik seviyesini epey azaltmak için harekete geçecek. Aksine eğer β→ 1 ise, gölün hareket (sökme) mekanizmaları (payda) mevcut mekanizmaya (pay) göre zayıftır. Diğer deyişle gölün özümleme kapasitesi en küçüktür. 24

Böylece gölün özümleme kapasitesi boyutsuz β sayısı tarafından değerlendirilebilir. Pay ve paydada oluşan akışın (debi) özümlemeyi hem artırdığı hem de azalttığını hesaba katın. Alıkonma süresi: E maddesinin alıkonma süresi τE sistemde E maddesinin molekül veya parçacığının kalacağı veya “alıkonacağı” zamanın ortalama miktarını gösterir. Kararlı hal, sabit hacimli sistem için şu şekilde tanımlanır; 25

(23) E: Hacimde E nin miktarı (ya M yada ML-3) ve = hem kaynak hem akışların mutlak değeri (ya MT-1 yada ML-3 T-1). Suyun yoğunluğu yaklaşık olarak 1 g/cm 3 olduğundan, göldeki suyun miktarı hacmine eşittir. Basit bir yaklaşımla göldeki suyun akışı dışa akışın yönüyle ölçülür (buharlaşma=yağış varsayımı). Bu değeri Eşitlik (23)’e koyarak suyun alıkonma süresini 26

(24) olarak buluruz. Bu ilişki basit bir fiziksel açıklamaya sahip olduğundan alıkonma süresinin genel fikrini anlamak için kullanışlıdır – göldeki su miktarının yerini almak için dışa akıştan dolayı gereken zaman. Yani gölün yıkama oranının ölçümüdür. Eğer hacim büyük ve debi küçükse göl uzun alıkonma süresine sahiptir; yani yavaş yıkayıcıdır. Aksi durumda kısa alıkonma süreli göller (yüksek debi ve küçük hacim) hızlı yıkayıcıdır. 27

Eşitlik 23 “kirlilik alıkonma süresini” hesaplamak için de kullanılabilir. (25) Bu eşitlik, Eşitlik 4 ile beraber, Eşitlik 23’e konulabilir ve şu elde edilir; (26) 28

Örnek 2: Transfer Fonksiyonu ve Alıkonma Süreleri Örnek 1 deki göl için (a) içe akış konsantrasyonu (b) transfer fonksiyonu (c) su alıkonma süresi ve (d) kirlilik alıkonma süresini belirleyin. Çözüm: (a) İçe akış konsantrasyonu şöyle hesaplanır: (b) Transfer katsayısı şimdi şu şekilde belirlenebilir Böylece taşıma prosesleri içe akış konsantrasyonunun %32 si olan göl konsantrasyonu oluştururlar. 29

(c) Alıkonma süresi şöyle hesaplanabilir, (d) Kirlilik alıkonma süresini Çürüme terimi ilavesi nedeniyle kirlilik alıkonma süresi su alıkonma süresinin yaklaşık ⅓’üdür. 30

Kirletici Azalmasında Geçici Durumlar Kararlı hal tahminlerine ek olarak, su-kalitesi yöneticileri doğal suların geçici tepkileriyle de ilgilidirler. Sistemin kararlı olduğunu farz edelim. Özel bir zamanda kirlilik giderme projesi yürütülür. Şekil 3. 4 de gösterildiği gibi iki soru ortaya çıkar: • Gelişmiş su kalitesinin meydana gelmesi ne kadar sürecek? • Geri kazanma “şekli” nasıl bir şeye benzeyecek? 31

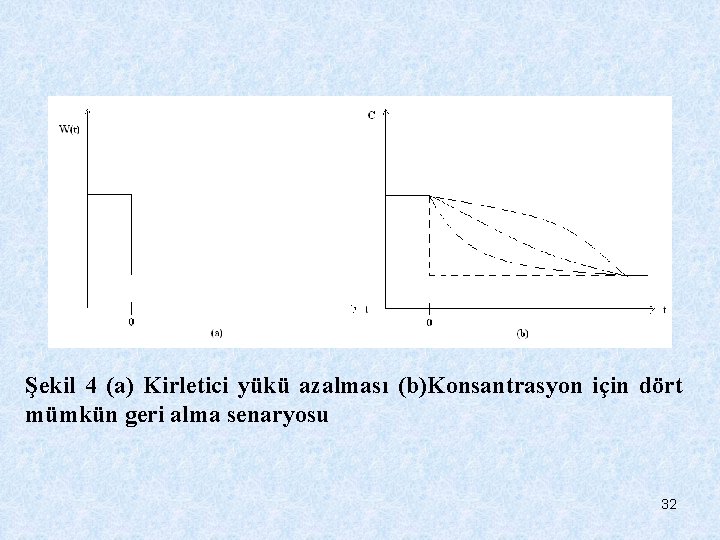
Şekil 4 (a) Kirletici yükü azalması (b)Konsantrasyon için dört mümkün geri alma senaryosu 32

Doğru yörüngeyi belirlemek için, kütle dengesi modeli ile başlayalım. (Eşitlik 16) (31) Bu eşitliği çözmeden önce, V ile bölebiliriz, (32) Terimleri toplayarak; (33) 33

(34) λ burada özdeğer olarak adlandırılır. (karakteristik bir değerdir. ) Tüm parametreler (Q, V, k, v, H) sabitse, Eşitlik 33 homojen olmayan, lineer, alışılmış diferansiyel denklemdir. Çözümü iki bölümden oluşur, (35) 34

Genel Çözüm Eğer t=0 anında c=c 0 ve W(t)=0 ise değişkenlerin ayılmasıyla çözülebilir. (36) Böylece göl konsantrasyonunun zamanın bir fonksiyonu olarak nasıl değiştiğini anlatan bir eşitliğe ulaşmış oluruz. 35

Tepki Süresi Her ne kadar λ parametre grubu açıkça gölün geçici tepki özelliklerini belirlese de, karar mercileri ile görüş alış verişi yapmak için noksanları vardır. İlk olarak, büyüdükçe göl için tepki süresinin azalması gibi beklenmeyen bir özelliğe sahiptir. İkinci olarak önceki bölümde belirtildiği gibi kesin matematiksel perspektif yüzünden şüphe altındadırlar, öncelikli temizleme prosesi hiçbir zaman tanımlanamaz. 36

Bütün bu kusurlar yeni bir parametre grubu çıkarmak için genel çözüm kullanılarak düzeltilebilir. Tepki süresi denilen, bu parametre grubu göl için geri kazanımın sabit yüzdesini tamamlamak için geçen zamanı gösterir. Böylece belirsizlik problemine geri kazanımın ne kadarının yeterli olacak şekilde tahmin edildiğini belirleyerek çare bulunur. Örneğin varsayalım ki eğer göl geri kazanımım %95 ini karşılasaydı tüm pratik amaçlar için geri kazandırıcı ölçümün başarılı olduğuna sevinecektik. 37

Eşitlik 36’nın terimlerinde %50 tepki süresi şu anlama gelir ki konsantrasyon ilk değerinin %50 sine azaltılmıştır. (37) t 50 : %50 tepki süresi (T). Üsteli 0. 5 C 0 a bölerek (38) elde ederiz Doğal logaritmasını aldığımızda; (39) şeklinde çözeriz. 38

0. 693 sayısı 2 nin doğal logaritmasıdır. t 50 niceliği genellikle yarılanma süresi olarak gösterilir. Yukarıdaki çıkarım keyfi bir tepki süresini hesaplamak için aşağıdaki formülle genelleştirilir: (40) : %Φ tepki süresidir. Örneğin nihai geri kazanılmış seviyenin %95 ine ulaşmak için ne kadar sürer belirlemesiyle ilgiliysek şunu hesaplayabiliriz; (41) 39

Örnek 4: Tepki Süresi Örnek 3 deki göl için %75, %90, %95 ve %99 tepki sürelerini belirleyiniz. Çözüm: %75 tepki süresi şöyle hesaplanabilir; (1. 39 tablodan alınmış değerdir) t 90 =3. 9 d t 95 =6. 4 d t 99 =9. 8 d Tepki Süresi t 50 t 63. 2 t 75 t 90 t 95 t 99 Formül 0. 693/λ 1. 39/λ 2. 3/λ 4. 6/λ 40

KISMİ ÇÖZÜMLER 41

Şimdiye kadar birincil kinetik CSTR için kütle denge eşitliği için kararlı durum ve genel çözümler çıkardık. (1) Şimdiki model için özdeğer λ şuna eşittir: (2) Kısmi çözümlere dönelim. Bunlar W(t) nin özel şekilleri için kapalı şekil çözümleriyle ilgilidir. Beklenildiği gibi çözümler sadece yükleme fonksiyonunun idealleştirilmiş biçimleri için mevcuttur. Kullanışlı durumlardan bazıları Şekil 1 de özetlenmektedir. 42

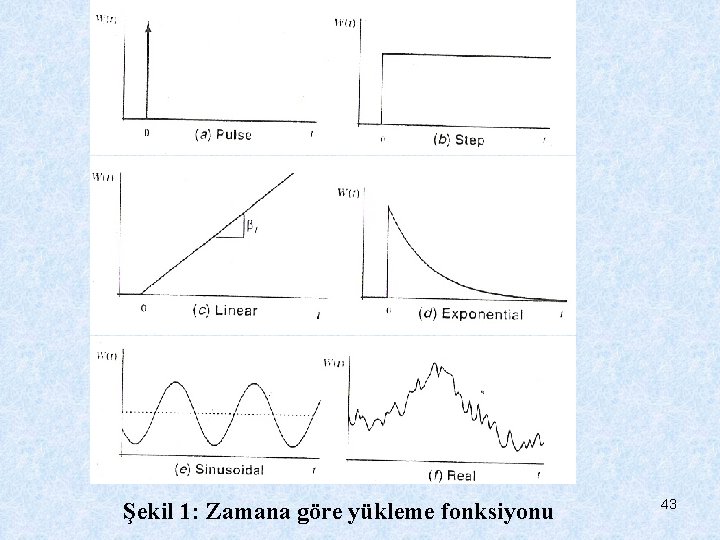
Şekil 1: Zamana göre yükleme fonksiyonu 43

Her ne kadar bu şekiller gerçekçi olması için çok idealize edilmiş olsa da üç neden için su kalitesi modellemesinde çok faydası vardır: • İlk olarak, yükleme eğilimlerinin uygun tahminlerini karşıladığı çok sayıda problem içerikleri vardır. • İkinci olarak, modeller gelecek etkilerini tahmin etmek için sıkça kullanılır. Sonuç olarak idealleştirme son derece kullanışlı hale gelir. 44

• Üçüncü olarak idealleştirilmiş yükleme fonksiyonları modelin nasıl çalıştığını daha iyi anlamamızı sağlar. Bu yüzden gerçek yükleme fonksiyonları (Şekil 1 f’ye bakın) model davranışını ayırt etmeyi zorlaştırır. Buna karşı idealleştirilmiş çözümler karmaşık olmayan bir görüş sağlar. İmpuls Yükleme (Dökülme) En temel W(t) biçimi nispeten kısa zaman periyodu boyunca atık deşarjını gösteren impuls yüklemedir. Kirleticinin su kütlesine kazara dökülmesi bu tiptendir. 45

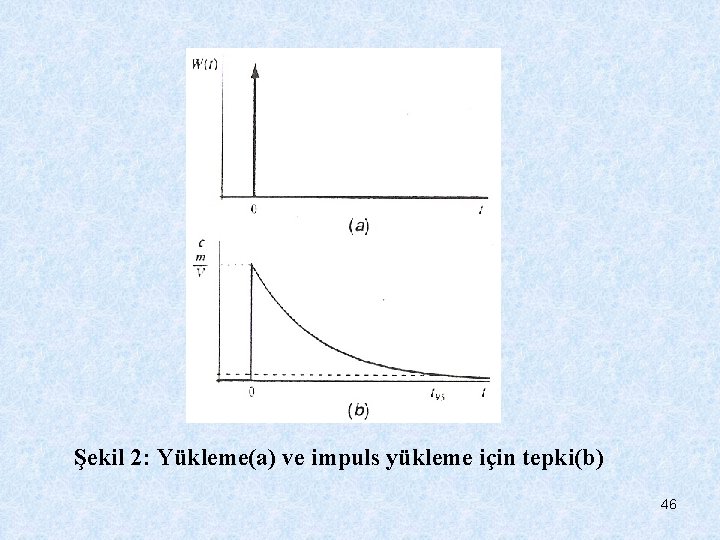
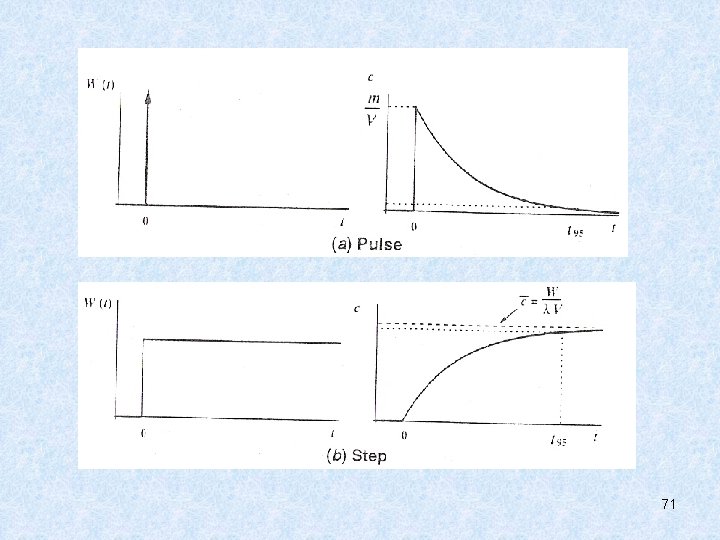
Şekil 2: Yükleme(a) ve impuls yükleme için tepki(b) 46

Matematik olarak “Dirac delta fonksiyonu” (veya impuls fonksiyonu) δ(t) bu tip bir olağanüstü durumu gösterme için geliştirilmiştir. Delta fonksiyonu merkezi t=0 da olan ve birim alana sahip sonsuz incelikte bir yükseliş olarak gösterilebilir. Aşağıdaki özelliklere sahiptir (Şekil 2 a): (3) (4) Kütlenin su hacmine impuls yükü delta fonksiyonunun terimlerinde gösterilebilir. 47

m: Dökülme (M) sırasında deşarj edilen kirletici kütlesinin miktarı ve delta fonksiyonu T-1 birimine sahiptir. Eşitlik 1’e koyarsak; (5) Bu durumda kısmi çözüm şöyledir; (6) Bu çözüm gösterdi ki dökülme aniden göl hacmi boyunca dağılır. Ondan sonra sonuç genel çözüme benzerdir; öyle ki konsantrasyon üstel olarak λ büyüklüğünce belirlenen bir oranda azalır. (Şekil 2 b) 48

Böylece iki şekil parametresinin impuls tepkisini özetlediğini görürüz. İlk konsantrasyon tepkinin yüksekliğini ifade eder: (7) ve tepki süresi onun geçici büyüklüğünü tanımlar. Eğer %95 tepki keyfi olarak seçilirse, (8) Eşik Yükleme (Yeni Kesintisiz Kaynak) Eğer t=0 da göl yüklemesi yeni sabit seviyeye değiştirilirse, zorlama fonksiyonu “eşik girdisi” olarak adlandırılır. Böyle bir davranış eşik fonksiyonu olarak 49 bilinen matematiksel bir anlatım ile verilir.

Bu aslında t=0 da sıçrama süreksizliğine sahip “onoff” fonksiyonudur. Şimdiki durum için, t=0 da yüklememizin sıfırdan W’ye sıçradığı durum, şu şekilde tanımlama yapılabilir; (9) W=yüklemenin yeni sabit seviyesi (M. T-1). Bu durum için kısmi çözüm; (10) Şekil 3 b’de gösterildiği gibi bu çözüm sıfırda başlar ve sonra asimptotik olarak yeni kararlı hal 50 konsantrasyonuna yaklaşır.

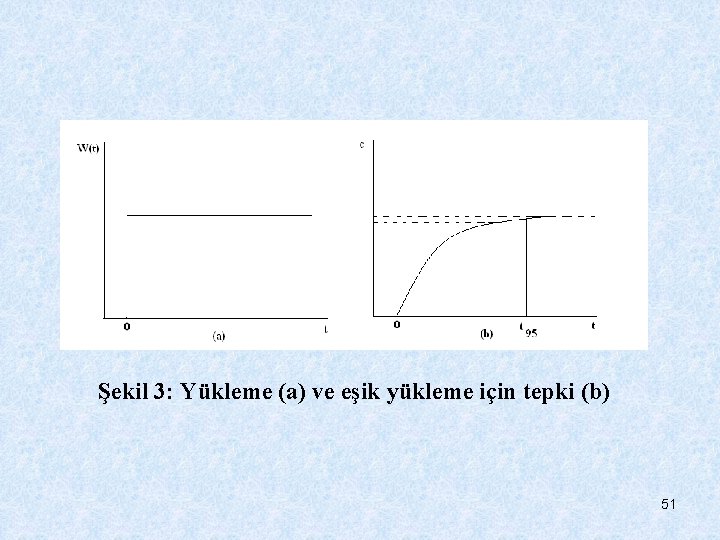
Şekil 3: Yükleme (a) ve eşik yükleme için tepki (b) 51

t= da Eşitlik (10) kararlı hal çözümüne eşit olur. (Eşitlik 17) (Üstel terim zaman ilerledikçe çok küçük olur. ) Böylece tekrar iki parametrenin eşik tepkisini özetlediğini görebiliriz. Kararlı hal konsantrasyonu tepkinin yüksekliğini tanımlar: (11) Ve tepki süresi onun geçici boyutunu tanımlar. Eğer %95 tepki rasgele seçilirse, Eşitlik (8) geçerli olur. 52

Örnek 1 Eşik Yükleme t=0 zamanında pissu işleme tesisi küçük bir alıkonma havuzuna (hacim=20*104 m 3) 200 mg/l konsantrasyonlu 10 MGD lik bir atıksu deşarjına başlıyor. Eğer pissu 0. 1 d-1 oranında çürürse, işlemin ilk iki haftası boyunca sistemdeki konsantrasyonu hesaplayınız. Ayrıca tesisin nihai etkisini değerlendirmek için şekil parametrelerini belirleyin. Çözüm: Debinin gereklidir. uygun birimlere çevrilmesi 53

Özdeğer şu şekilde tanımlanabilir: Bu yüzden konsantrasyon Eşitlik 10 ile şu şekilde hesaplanabilir: =31. 83 (1 -e-0. 118927 t) İlk 2 hafta için sonuçlar şöyledir: t(d) 0 2 4 6 8 10 12 14 C(mg/l) 0 6. 74 12. 05 16. 24 19. 54 22. 14 24. 19 25. 81 54

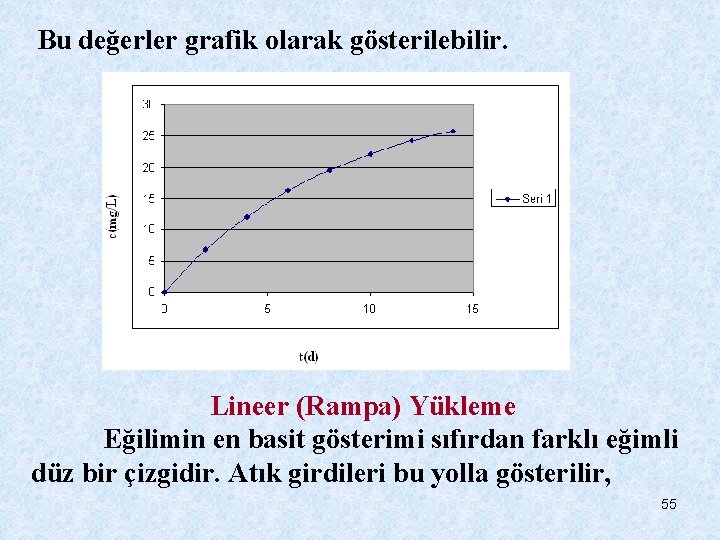
Bu değerler grafik olarak gösterilebilir. Lineer (Rampa) Yükleme Eğilimin en basit gösterimi sıfırdan farklı eğimli düz bir çizgidir. Atık girdileri bu yolla gösterilir, 55

(12) βl = Eğilimin eğim veya değişim oranı (MT-2). Dikkat ediniz ki eğilim hem pozitif hem de negatif olabilir. Bu durum için kısmi çözüm şöyledir: (13) Su kalitesi uygulamalarında, pozitif olarak artan durum (Şekil 4 a) çok daha sık kullanılır. Nüfus büyümesine oranlı bazı yüklemelere burada uygun şekilde yaklaşılabilir. Bu gibi durumlar için, ilk başlangıç zamanından sonra (3/ λ ya eşit olan %95 tepki süresi olarak tanımlanabilen zaman), çözüm şu hale gelir; 56

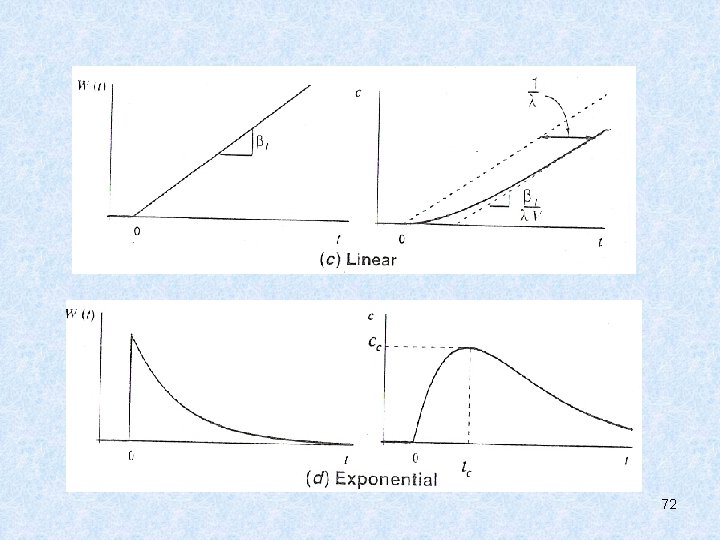
Şekil 4: Yükleme (a) ve Lineer artan yükleme için tepki (b) 57

(14) Böylece şekil 4 b’de açıklandığı gibi çözüm neticede sabit bir eğimde artar. (15) (16) Üstel Yükleme yönelimlerini nitelendiren diğer bir standart yol üstel fonksiyon gibidir. (Şekil 5 a) (17) 58

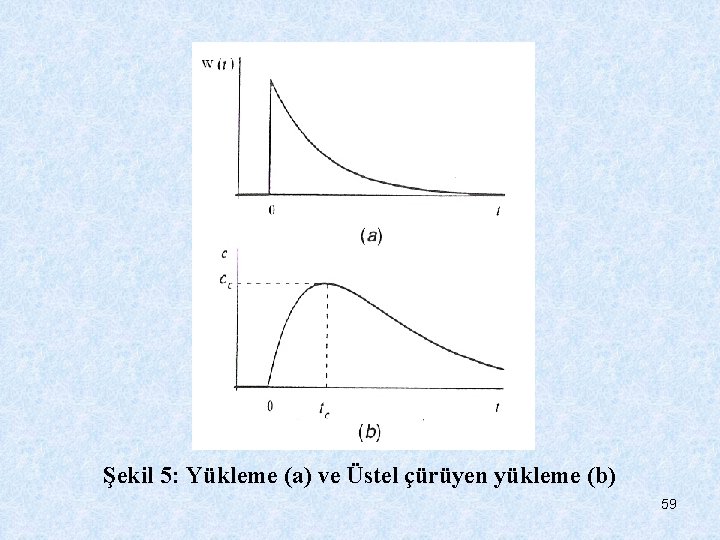
Şekil 5: Yükleme (a) ve Üstel çürüyen yükleme (b) 59

Burada We: t=0’daki değeri gösteren parametre (MT-1) ve βe yüklemenin büyüme (pozitif) veya çürüme oranını gösterir. (T-1) Böyle bir fonksiyon kendi büyüklüklerine oranla büyüyen yada çürüyen atık kaynaklarını nitelendirir. Bu durum için kısmi çözüm, (18) Bu çözüm su kalitesi modellemesinde birçok uygulamaya sahiptir. Pozitif üstel, nüfus büyümesine dayalı model yüklemeleri için kullanılır. Çürüme üsteliyle daha yaygın karşılaşılır çünkü birinci derece çürüme proseslerine uygulanır. 60

Şekil 5 b üstel çürüme yükü için sonuç gösterir. Çözümün pik seviyeye nasıl ulaştığına ve sonra nasıl üstel olarak azalmaya başladığına dikkat edelim. Böylece görüyoruz ki iki şekil parametresi vardır: büyüklük ve pik zamanı. Zaman eşitlik 18’i diferansiyelleyerek ve sonucunu sıfıra eşitleyerek kolayca belirlenir. Bazı cebirsel oynamalardan sonra pik zamanı şöyle belirlenebilir: (19) Burada c indisi gösterir ki bu “kritik” konsantrasyonun zamanıdır. 61

Büyüklük sadece eşitlik (19)’u eşitlik (18)’e koyarak belirlenir. Alternatif bir yaklaşım, eşitlik (17)’ye (negatif üslü) ve dc /dt =0’a eşit yükleme ile, eşitlik (1)’e bağlı pik konsantrasyonu tanıyarak geliştirilebilir. dc /dt =0 ile, kritik zamanı eşitlik (1)’e koyarsak şunu elde ederiz: (20) Bundan başka, eşitlik (19) eşitlik (20)’ye sokulabilir ve sonuç şunu vermesi için ayarlanır: (21) 62

Örnek 2 Üstel Zorlama Fonksiyonu: Birinci derece reaksiyonların takibinden serileri toplu reaktörlerde yer alır: Bu reaksiyonların kütle denge denklemleri şöyle yazılabilir: CA 0=20 ve CB 0=0 mg/l olan bir deneyin yürütüldüğünü varsayın. Eğer k 1=0. 1 ve k 2=0. 2 d-1 ise, zamanın bir fonksiyonu olarak B reaktantının konsantrasyonunu hesaplayın. Ayrıca, şekil parametrelerini belirleyin. 63

Çözüm: A reaktantının konsantrasyonu ilk diferansiyel eşitliği integre ederek belirlenebilir. Bu sonuç ikinci diferansiyel denkleme sokulabilir; Böylece kütle dengesi üstel zorlama fonksiyonuyla birincil derece diferansiyel denklem şeklindedir. Çözüm şöyledir; 64

veya parametre değerlerini yerine koyarak; Bu çözümün çizimi, CA için çözümle birlikte, şekil E 2’de gösterilmektedir. Bu durum için şekil parametreleri şu şekilde hesaplanır: Bu değerler grafikle tutarlıdır. 65

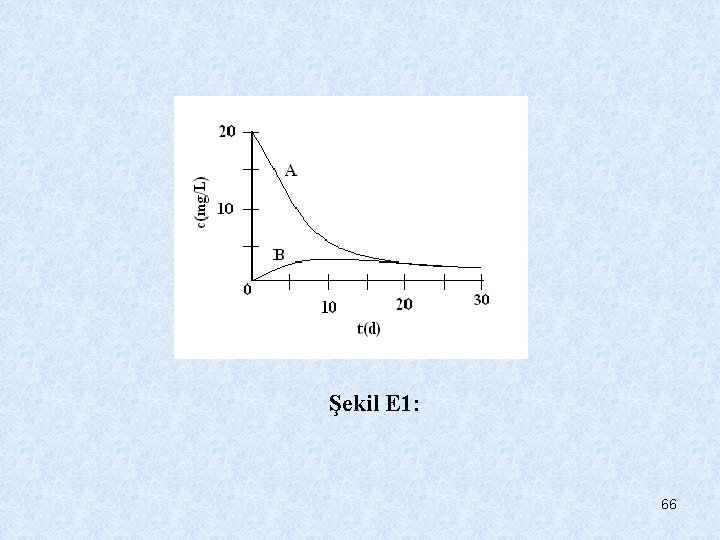
Şekil E 1: 66

Sinüzoidal Yükleme En basit periyodik giriş matematiksel olarak aşağıdaki gibi gösterilebilen sinüzoidal fonksiyondur (şekil 6 a) (22) Burada, : ortalama yükleme(MT-1) Wa: yükleme genliği(MT-1) θ: faz değişikliği(radyan) ω: salınımın açısal frekansı(radyan T-1) (23) 67

Burada Tp=salınımın periyodu (T). Salınımın basit frekansı şöyle hesaplanır: (24) Eşitlik (22) dört şekil parametresine sahiptir. Bunlar ω (sinüs dalga salınımı sıklığı), ( sinüs dalgası için ortalama değer), Wa (salınım sallanmalarının düşeydeki büyüklüğü) ve θ (fonksiyonun standart sinüs dalgalarına göre yatay olarak ne kadar değiştiği). Böylece parametreler sinüzoidal yükü karakterize etmek için birçok esneklik sağlar. 68

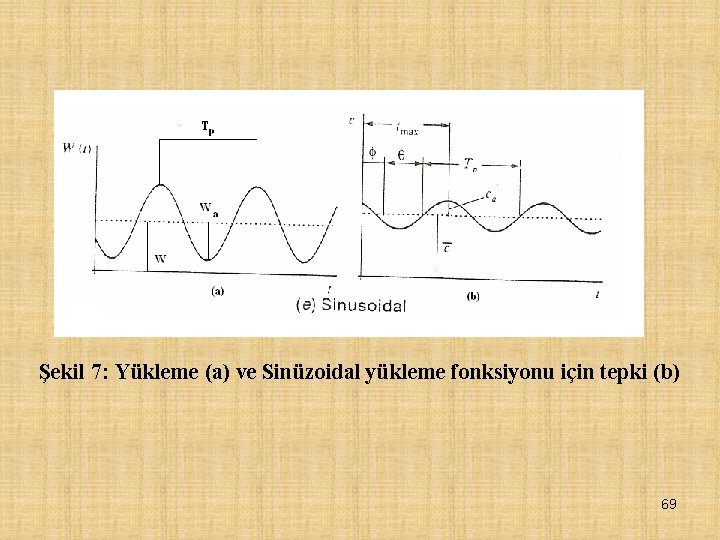
Şekil 7: Yükleme (a) ve Sinüzoidal yükleme fonksiyonu için tepki (b) 69

Toplam Çözüm: Doğrusallık ve Zaman Değişimleri Şekil 7 geliştirdiğimiz analitik çözümleri özetlemektedir. Her ne kadar kendi doğrularında kullanışlı olsalar da, aynı zamanda benzer yükleme eğilimlerinin etkisini değerlendirmek için ardına kullanılabilir. Öyle ki, cpi ve ai’nin herhangi sabitler olduğu kısmi çözümlerin bir değerini çıkarırsak, toplam çözüm genel ve kısmi çözümlerin basit bir toplamı olarak çıkarılabilir. (33) 70

71

72

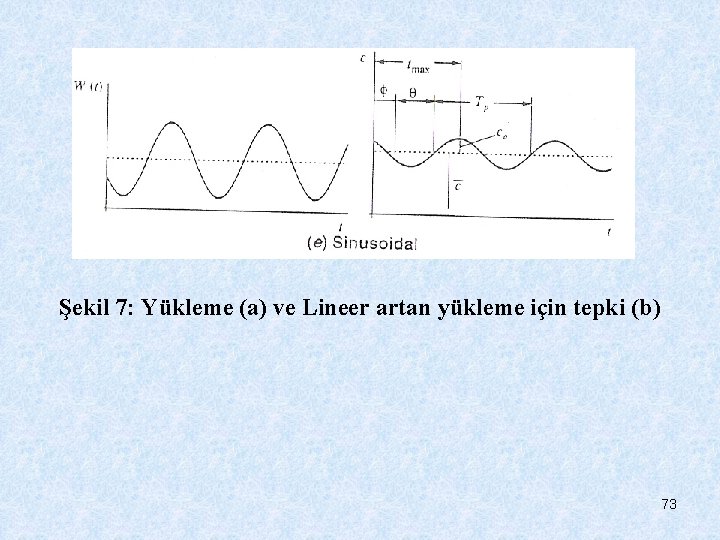
Şekil 7: Yükleme (a) ve Lineer artan yükleme için tepki (b) 73

Buna ek olarak sadece çözümleri değiştirerek farklı zamanlarda başlayan yükleri ekleyebiliriz. Eğer c(t) fonksiyonuna sahipseniz ve gelecekte zamanın o birimlerine değiştirmek istiyorsanız sadece bağımsız değişken a’yı çıkaracaksınız, c(t-a). Örneğin iki impuls yüke sahip olduğumuzu varsayalım, biri sıfır anında diğeri a anında oluşur. Sonuç konsantrasyonları eşitlik 6 kullanarak şu şekilde hesaplanabilir. 0≤t<a (34) t≥a (35) 1 ve 2 indisleri sırasıyla t=0 ve t=a anındaki impuls yüküne göre çözümleri gösterir. 74

Örnek 4 Lineer ve Üstel Yüklemeler O’Cannor ve Mueller(1970) Michigan Gölü’ne konservatif madde klorürün yüklemelerini karakterize etmek için lineer ve üstel zorlama fonksiyonlarını kullandı. Örneğin yol tuzu yüzünden klorür yüklemelerini lineer modelle karakterize ettiler. t<1930≤t≤ 1960 W(t) g/yıl birimindedir. Havzada nüfus büyümesiyle ilgili olan tuzun diğer kaynaklarını karakterize etmek için üstel model kullandılar. (örneğin kentsel ve endüstriyel kaynaklar), 75

t<1900≤t≤ 1960 O’Cannor ve Mueller’e göre, Michigan Gölü 1900’den 1960’a olan periyot için aşağıdaki ortalama özelliklere sahiptir: dışaakış=49, 1*109 m 3/yıl ve hacim=4880*109 m 3 1900’den 1960’a kadar olan Michigan Gölü’ndeki klorür konsantrasyonunu hesaplayın. Çözüm: Klorürün konservatif parametre olmasından, özdeğer basitçe alıkonma süresinin yerine geçer. 76

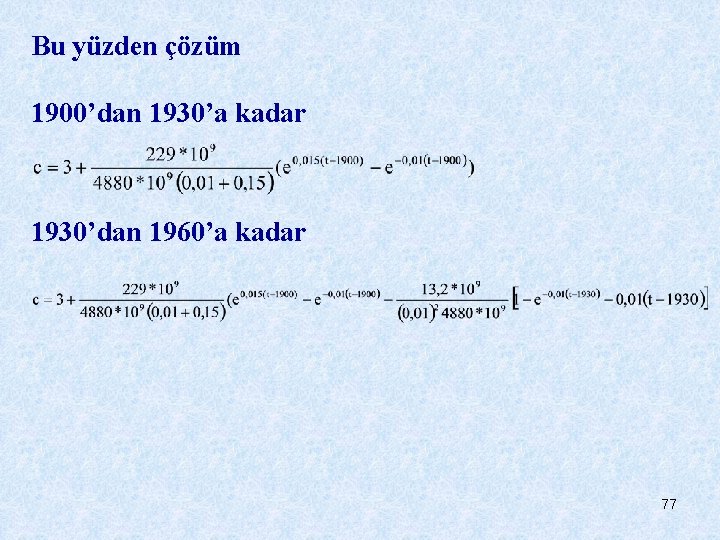
Bu yüzden çözüm 1900’dan 1930’a kadar 1930’dan 1960’a kadar 77

ilginiz için Tesekkürler. . . 78