TC Mhendislik ve Tasarm Fakltesi Endstri Mhendislii Blm

İTİCÜ Mühendislik ve Tasarım Fakültesi Endüstri Mühendisliği Bölümü İSTATİSTİK VE OLASILIK I 10. Hafta: Örnekleme Teorisi Öğr. Gör. Berk Ayvaz 2013

Örnekleme Teorisi Modern istatistiğin en önemli görevi, anakütle parametrelerinin örneklem değerleri (örnek istatistikleri) yardımıyla tahmin edilmesine imkan sağlamaktır. Uygulamada, bütün anakütlenin incelenmesi çoğu zaman mümkün olmamaktadır. Bunun yerine söz konusu anakütleden alınan bir rassal örneklemin incelenmesi yoluna gidilmektedir. Elde edilen örnek değerlerinin anakütle parametresi yerine kullanılabilmesi için iki önemli şart vardır. 1. Anakütledeki her birimin örneğe girme şansının eşit olmasıdır. 2. Örneğin yeterince büyük olmasıdır. Bu ikinci şarta göre anakütle büyü dükçe örneğin de büyük tutulması gerekecektir.

Örnekleme Teorisi Örnekleme ya iadeli veya iadesiz olur. Çekilen birimin anakütleye tekrar iade edilmesi halinde iadeli örnekleme, aksi halde iadesiz örnekleme söz konusudur. Herhangi bir anakütle birimi, iadeli örneklemede örneğe bir kaç kere girebileceği halde, iadesiz örneklemede bir kere girer. Örnekleme ya sınırlı veya sınırsız anakütleler için yapılır. Örneklemenin iadeli olarak yapıldığı sınırlı bir anakütle sınırsız kabul edilir.

Örnekleme Teorisi

Ortalamaların Örnek Dağılımı

Ortalamaların Örnek Dağılımı
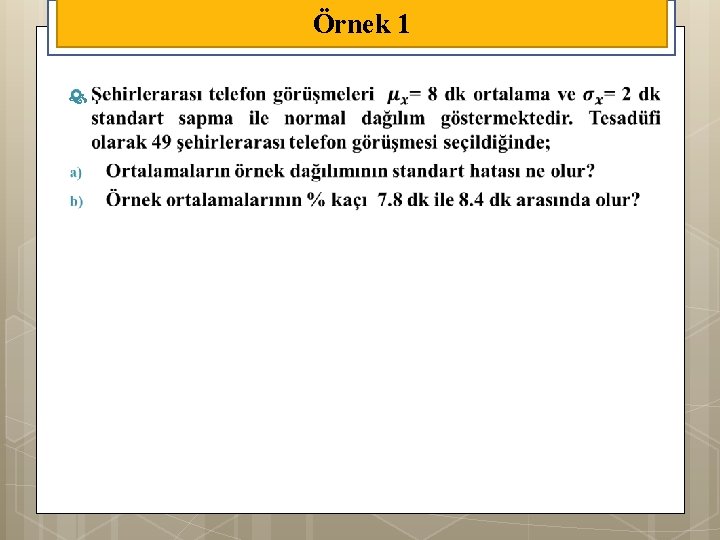
Örnek 1

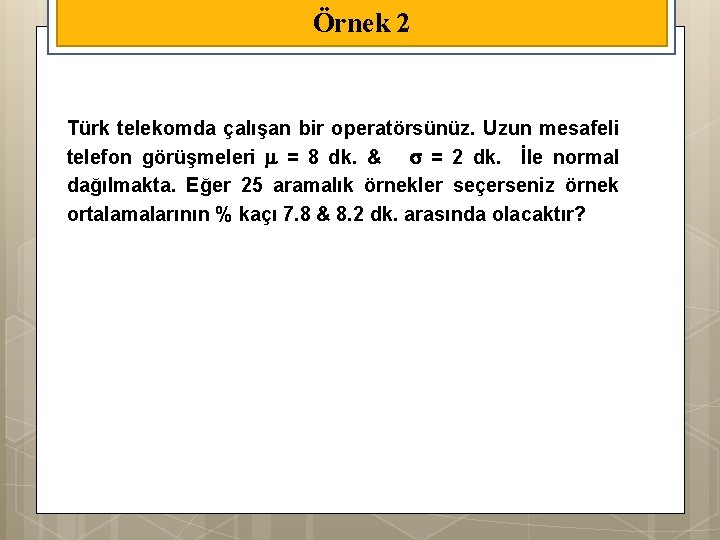
Örnek 2 Türk telekomda çalışan bir operatörsünüz. Uzun mesafeli telefon görüşmeleri = 8 dk. & = 2 dk. İle normal dağılmakta. Eğer 25 aramalık örnekler seçerseniz örnek ortalamalarının % kaçı 7. 8 & 8. 2 dk. arasında olacaktır?
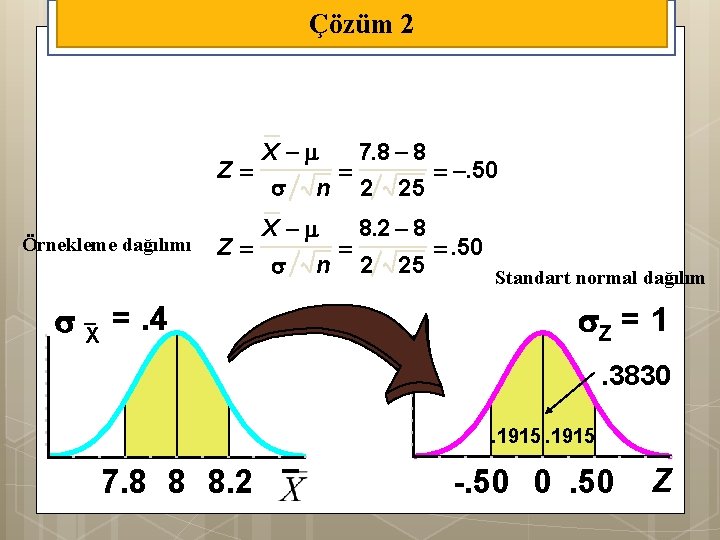
Çözüm 10 2 X 7. 8 8 Z . 50 n 2 25 Örnekleme dağılımı Z X =. 4 n 8. 2 8 2 25 . 50 Standart normal dağılım Z = 1. 3830. 1915 7. 8 8 8. 2 -. 50 0. 50 Z
Örnek 3 Bir sanaayi kuruluşunda çalışanların gündelikleri 800 TL ortalama ve 90 TL standart sapmaya sahiptir. Rasgele seçilen 81 işçinin gündeliklerinin ortalamasının 810 TL ile 825 TL arasında olma olasılığı nedir?

Örnek 4 Bir üreticiye göre rulmanların ömrü ortalaması 36. 000 standart sapması 4. 000 mil olan bir normal dağılıma uymaktadır. 16 rulman içeren rassal bir örneklemde ortalama ömür 34. 500 mildir. Buna göre rassal seçilen bir rulmanın ortalama değerde yada daha düşük ömre sahip olma olasılığı nedir?

Çözüm 4 =1 -0, 9332=0, 0668
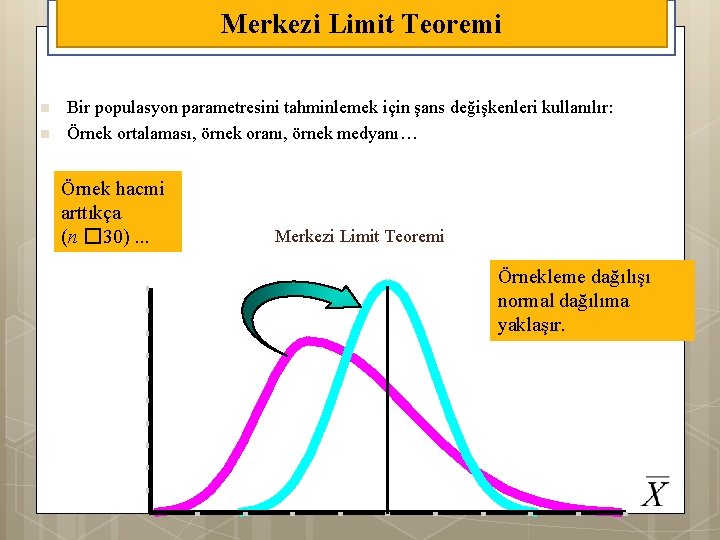
Merkezi Limit Teoremi 15 n n Bir populasyon parametresini tahminlemek için şans değişkenleri kullanılır: Örnek ortalaması, örnek oranı, örnek medyanı… Örnek hacmi arttıkça (n � 30). . . Merkezi Limit Teoremi Örnekleme dağılışı normal dağılıma yaklaşır.

Merkezi Limit Teoremi

Merkezi Limit Teoremi

Merkezi Limit Teoremi
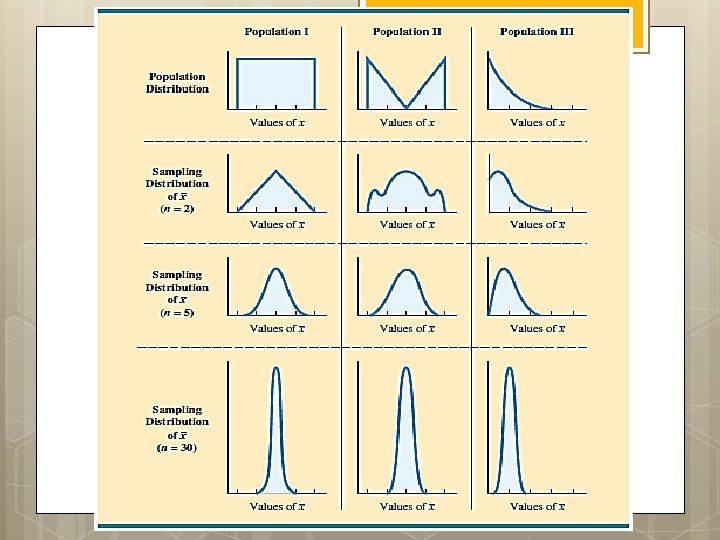

Örnek 5


Oranların Örnek Dağılımı
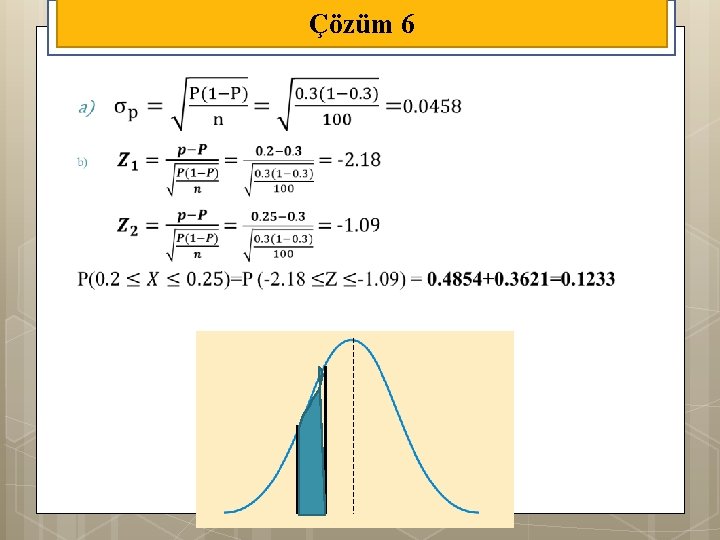
Örnek 6 Büyük bir alış-veriş merkezinde 15 TL’dan alışveriş yapan müşterilerin %30’unun kredi kartı kullandığı tesbit edilmiştir. 15 TL’dan fazla alışveriş yapan 100 müşteri için oranların örnek dağılımının standart hatası ne olur? 15 TL’dan fazla alışveriş yapan 100 müşteriden %20 ile %25’inin kredi kartı kullanması ihtimalini bulunuz.
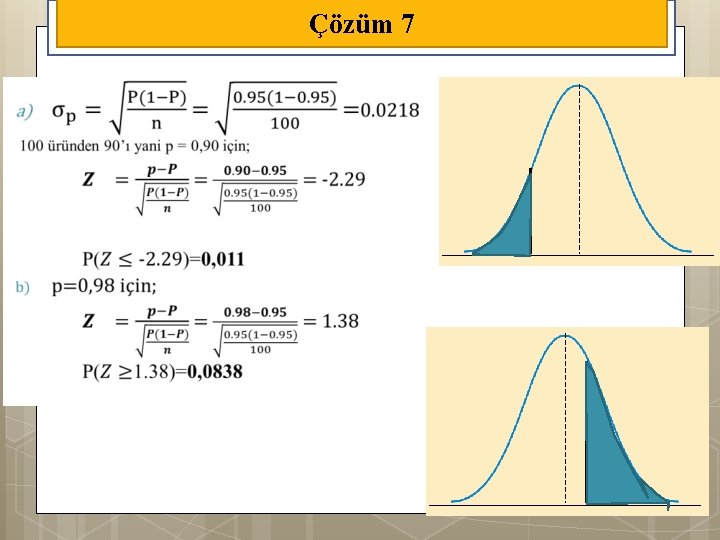
Örnek 7 Bir imalatçı herbiri 100 elektrik ampülünden meydana gelen 1000 koli ampül gönderiyor. Ampüllerin %95 ’i sağlam olduğuna göre kolilerin kaç tanesinde, a) 90 taneden az sağlam ampül b) 98 veya daha fazla sağlam ampül çıkacağını hesaplayınız.

Ortalamalar Arası Farkların Örnek Dağılımı

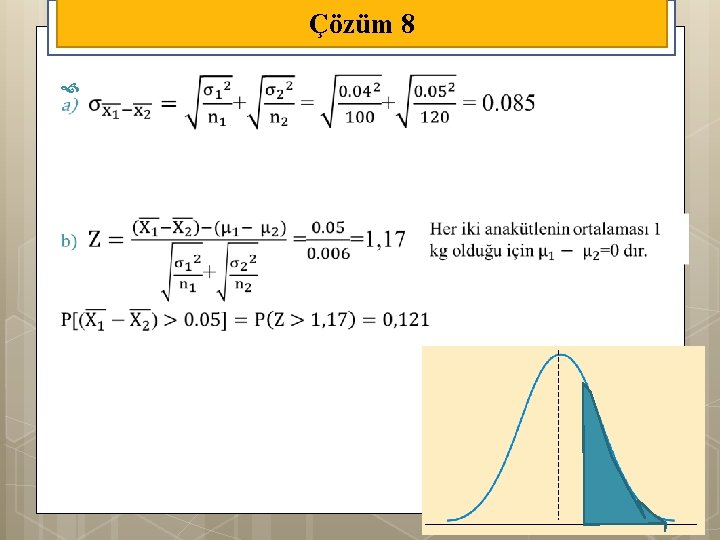
Örnek 8
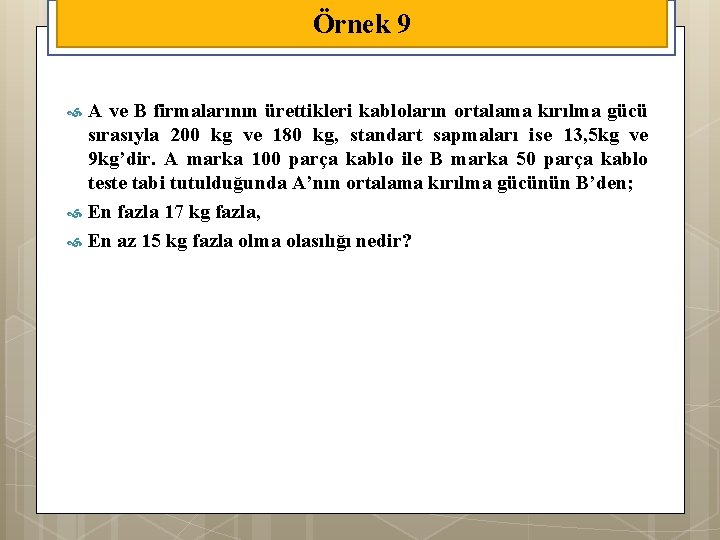
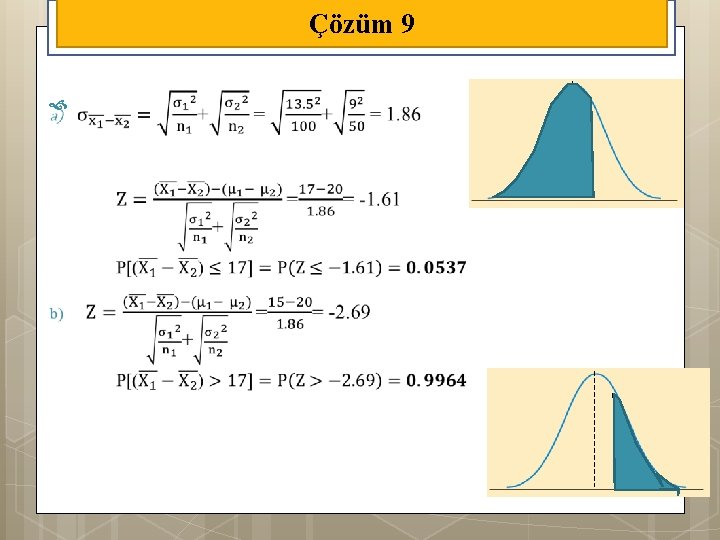
Örnek 9 A ve B firmalarının ürettikleri kabloların ortalama kırılma gücü sırasıyla 200 kg ve 180 kg, standart sapmaları ise 13, 5 kg ve 9 kg’dir. A marka 100 parça kablo ile B marka 50 parça kablo teste tabi tutulduğunda A’nın ortalama kırılma gücünün B’den; En fazla 17 kg fazla, En az 15 kg fazla olma olasılığı nedir?

Oranlar Arası Farkların Örnek Dağılımı

Örnek 10 Birinci fabrikadaki kusurlu mamul oranının 0. 08 ve ikinci fabrikadaki kusurlu mamul oranının 0. 05 olduğu bilinmektedir. Tesadüfi olarak birinci fabrikadan 100, ikinci fabrikadan 150 mamul seçilmiş ve birinci örnek teki kusurlu mamul oranı 0. 09, ikinci örnekteki kusurlu mamul oranı 0. 06 olarak gözlenmiştir. a) Buna göre kusur oranları arasındaki farkın standart hatasını bulunuz. b) Fabrikalardaki kusurlu mamul oran ları arasındaki farkın en fazla 0. 01 olması ihtimalini hesaplayınız.
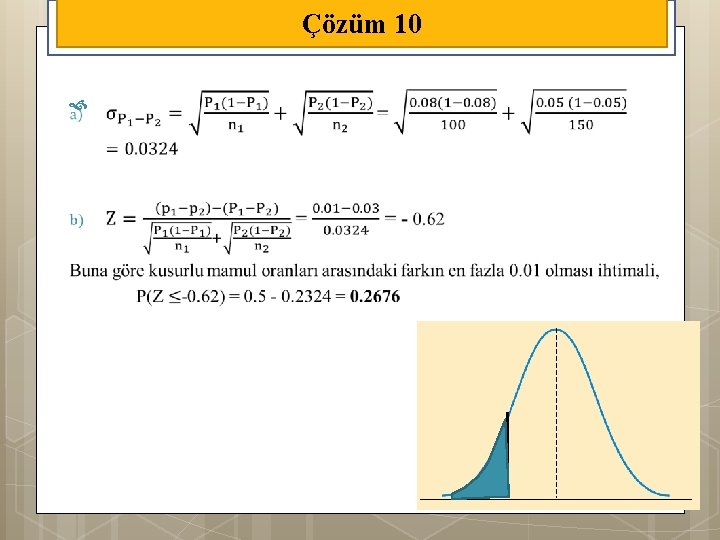
Çözüm 10
Örnek 11 A fabrikasında imal edilen pillerin %80’i 200 saatin üzerinde performans sağlarken, B fabrikasında üretilen pillerin %73’ü 200 saatin üzerinde performans sağlayabilmektedir. A fabrikasından 50 ve B fabrikasından 60 pil incelemeye tabi tutulursa performans oranları arasındaki farkın en az %10 olma ihtimali nedir?
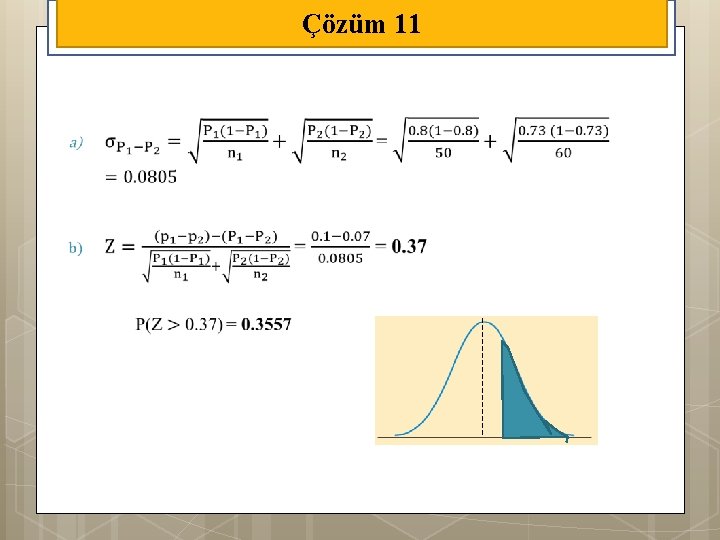
Çözüm 11
- Slides: 36