Module 17 TwoSample ttests with equal variances for





















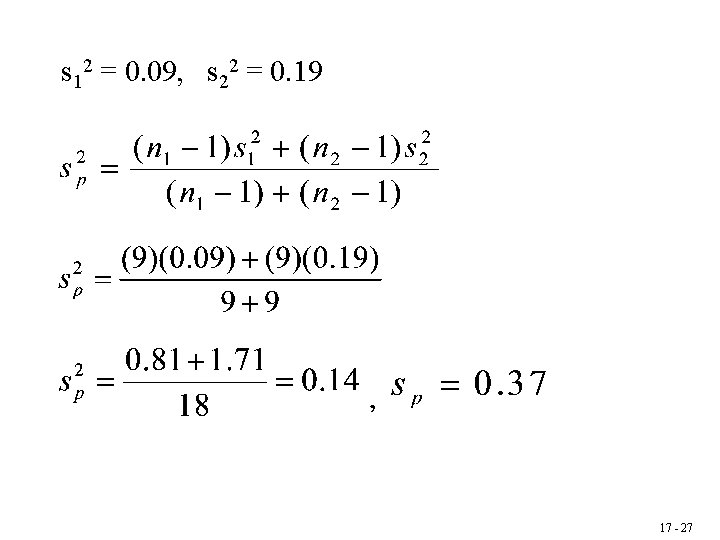




- Slides: 34

Module 17: Two-Sample t-tests, with equal variances for the two populations This module describes one of the most utilized statistical tests, the two-sample t-test conducted under the assumption that the two populations from which the two samples were selected have the same variance. Reviewed 11 May 05 /MODULE 17 17 - 1

The General Situation Up to this point, the focus has been on a single population, for which the observations had a normal distribution with a population mean and standard deviation . From this population, a random sample of size n provided the sample statistics and s as estimates of and , respectively. We created confidence intervals and tested hypotheses concerning the population mean , using the normal distribution when we had available the value of and using the t distribution when we did not and thus used the estimate s from the sample. This circumstance is often described as the one sample situation. 17 - 2

Clearly, we are often faced with making judgments for circumstances that involve more than one population and sample. For the moment, we will focus on the so-called two sample situation. That is, we consider two populations. City A City B Mean µA µB SD A B Question: Do you believe the two populations have the same mean? 17 - 3

Two Sample Hypotheses H 0: A = B versus H 1: A B or equivalently H 0: Δ = A - B = 0 versus H 1: Δ = A - B 0. 17 -

Parameters vs. Estimates 17 - 4

We are interested in Δ = µ 1 - µ 2 If the samples are independent, then When 17 - 5

Estimating σ2 we have two estimates of σ2 , one from sample 1, namely s 12 and one from sample 2, namely s 22. How can we best use these two estimates of the same thing. One obvious answer is to use the average of the two; however, it may be desirable to somehow take into account that the two samples may not the same size. If they are not the same size, then we may want the larger one to count more. 17 - 6

Pooled Average Hence, we use the weighted average of the two sample variances, with the weighting done according to sample size. This weighted average is called the pooled estimate: 17 - 7

Estimate of Var( ) To estimate Var( ), we can use 17 - 8

Example 1: Blood Pressures of Children To investigate the question of whether the children of city A and city B have the same systolic blood pressure, a random sample of n = 10 children was selected from each city and their blood pressures measured. These samples provided the following data: 17 - 9

We are interested in the difference: Δ = A - B and we have as an estimate of A and as an estimate of B; hence it is reasonable to use: d = - = 105. 8 - 97. 2 = 8. 6 (mm Hg) as an estimate of Δ = A - B. 17 - 10

We then can ask whether this observed difference of 8. 6 mm Hg is sufficiently large for us to question whether the two population means could be the same, that is, A = B. Clearly, if the two population means are truly equal, that is, if A = B is true, then we would expect the two sample means also to be equal, that is = , except for the random error that occurs as a consequence of using random samples to represent the entire populations. The question before us is whether this observed difference of 8. 6 mm Hg is larger than could be reasonably attributed to this random error and thus reflects true differences between the population means. 17 - 11

Confidence Interval for A- B, using sp 17 - 12

17 - 13

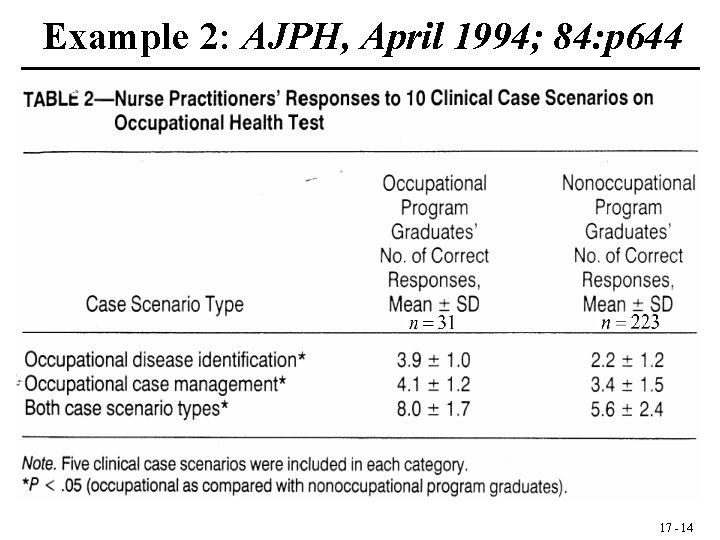
Example 2: AJPH, April 1994; 84: p 644 17 - 14

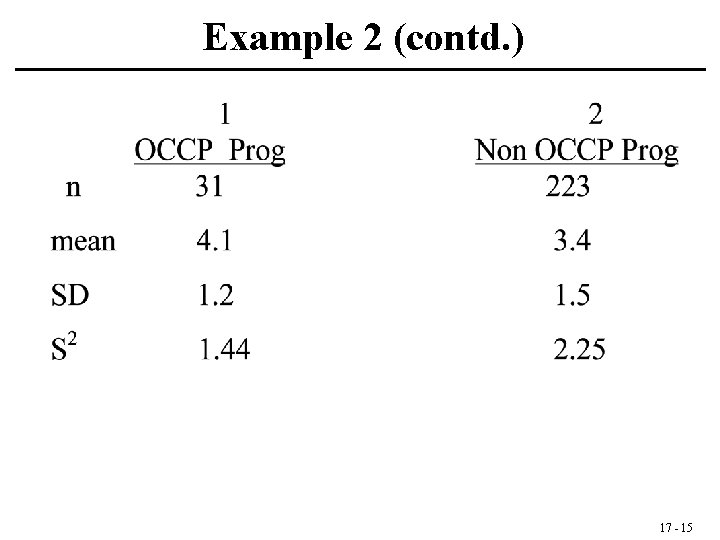
Example 2 (contd. ) 17 - 15

Example 2 (contd. ) 1. The hypothesis: H 0 : 1 2 vs. H 1: 1 2 2. The assumptions: Independent random samples from normal distributions, 3. The level: = 0. 05 4. The test statistic: 5. The critical region: Reject H 0 if t is not between 17 - 16

6. Test result: 7. The Conclusion: Reject H 0 since t = 2. 5 is not between ± 1. 97; 0. 01 < p < 0. 02 17 - 17

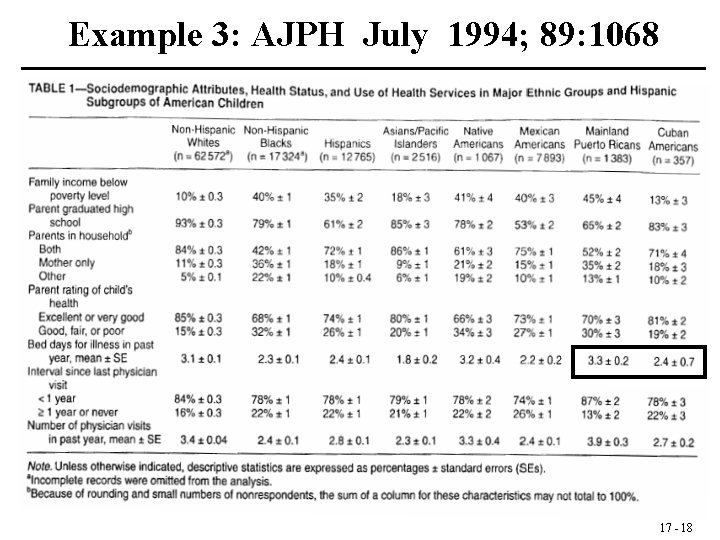
Example 3: AJPH July 1994; 89: 1068 17 - 18

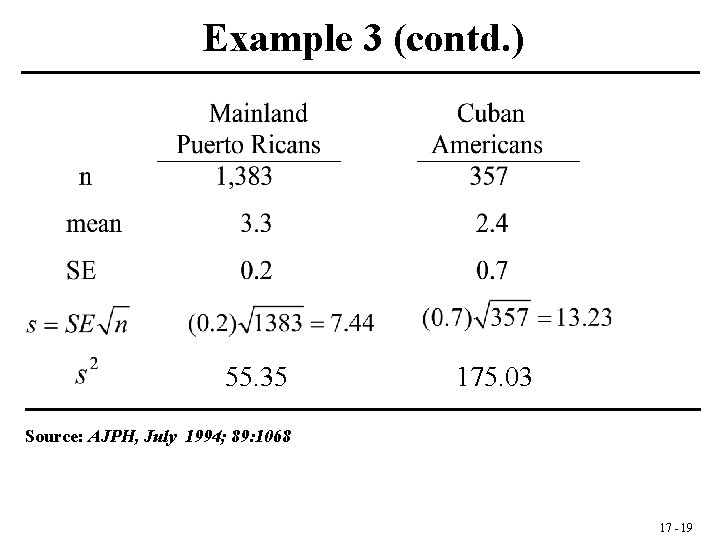
Example 3 (contd. ) 55. 35 175. 03 Source: AJPH, July 1994; 89: 1068 17 - 19

1. The hypothesis: H 0 : µ 1 = µ 2 vs. H 1: µ 1 ≠ µ 2 2. The assumptions: Independent random samples from normal distributions 3. The level: = 0. 05 4. The test statistic: 17 - 20

5. The critical region: Reject if t is not between t 0. 975(1738) =1. 96 6. The Result: 7. Conclusion: Accept H 0: 1 = 2, since p > 0. 05 ; 0. 05 < p < 0. 10 17 - 21

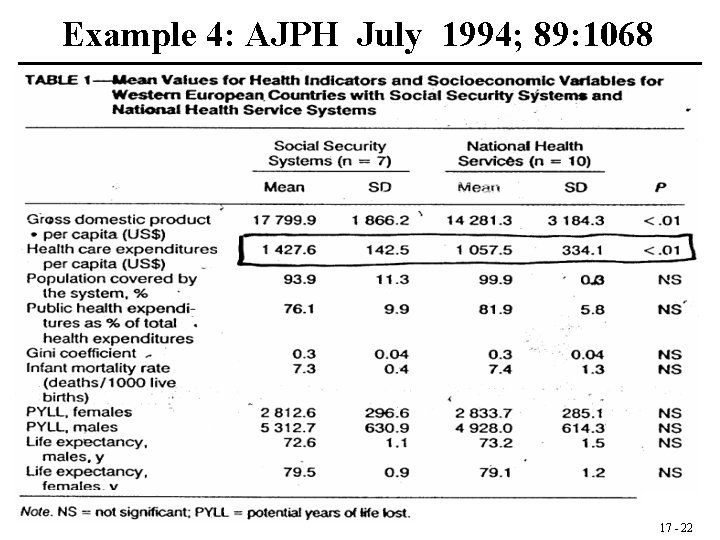
Example 4: AJPH July 1994; 89: 1068 17 - 22

1. The hypothesis: 2. The level: H 0: SSS = NHS vs. H 1: SSS ≠ NHS = 0. 05 3. The assumptions: Independent Samples, Normal Distribution, 4. The test statistic: 5. The critical region: Reject if t is not between ± 2. 1315 17 - 23

6. The result : 7. The conclusion: Reject H 0: SSS = NHS ; 0. 01< p < 0. 02 17 - 24

Independent Random Samples from Two Populations of Serum Uric Acid Values 17 - 25

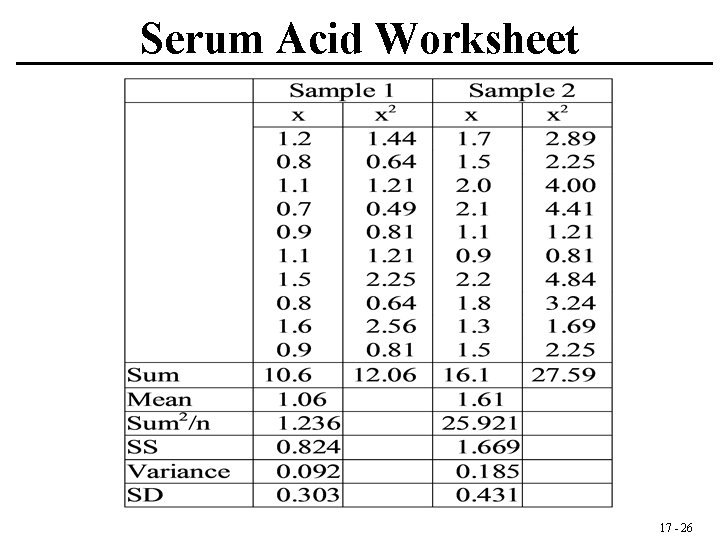
Serum Acid Worksheet 17 - 26
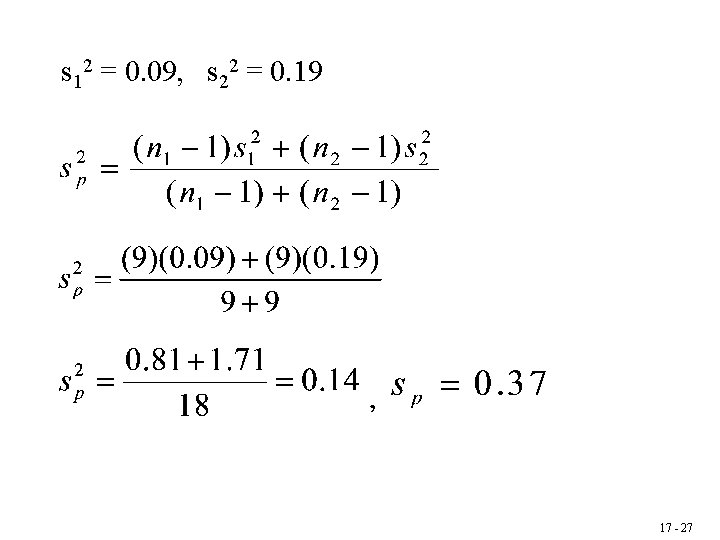
s 12 = 0. 09, s 22 = 0. 19 17 - 27

Testing the Hypothesis That The Two Serum Uric Acid Populations Have The Same Mean 1. The hypothesis: H 0: μ 1 = μ 2 vs. H 1: μ 1 ≠ μ 2 2. The -level: = 0. 05 3. The assumptions: Independent Random Samples Normal Distribution, 4. The test statistic: 17 - 28

5. The reject region: Reject H 0: μ 1 = μ 2 if t is not between ± t 0. 975(18) = 2. 1009 6. The result: 7. The conclusion: Reject H 0: μ 1 = μ 2 , since t is not between ± 2. 1009 17 - 29

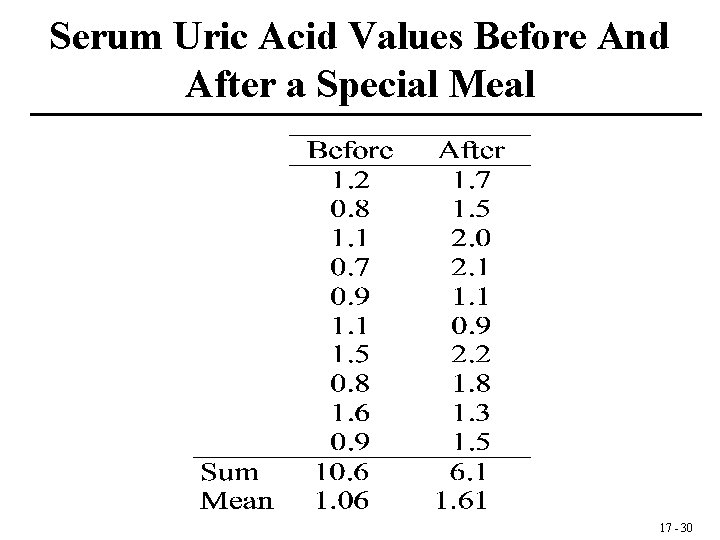
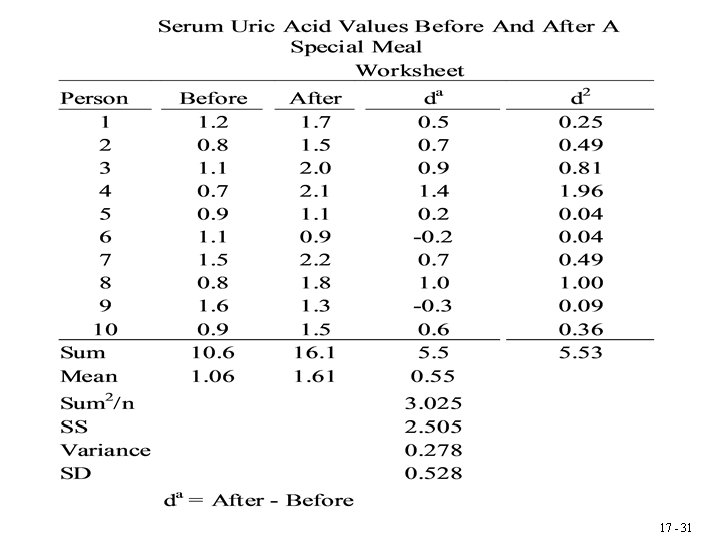
Serum Uric Acid Values Before And After a Special Meal 17 - 30

17 - 31

Testing the Hypothesis That The Serum Uric Acid Levels Before and After A Special Meal Are The Same 1. The hypothesis: H 0: Δ = 0 vs. H 1: Δ ≠ 0, where Δ = μAfter - μBefore 2. The -level: = 0. 05 3. The assumptions: Random Sample of Differences, Normal Distribution 4. The test statistic: 17 - 32

5. The rejection region: Reject H 0: Δ = 0, if t is not between ± t 0. 975(9) = 2. 26 6. The result: 7. The conclusion: Reject H 0: Δ = 0 since t is not between ± 2. 26 17 - 33
 Equal sharing and equal grouping
Equal sharing and equal grouping Are opposite angles equal
Are opposite angles equal Equal height equal light
Equal height equal light Meridionalnet
Meridionalnet Taku komura
Taku komura Performance evaluation using variances from standard costs
Performance evaluation using variances from standard costs Direct labor variances categories
Direct labor variances categories Ap statistics rules for means and variances
Ap statistics rules for means and variances Comparing two population variances
Comparing two population variances How to calculate random variable
How to calculate random variable Total fixed overhead cost formula
Total fixed overhead cost formula Standard cost operating statement
Standard cost operating statement Cohen manion morrison
Cohen manion morrison Direct materials variances
Direct materials variances C device module module 1
C device module module 1 Elektronik för barn
Elektronik för barn Adressändring ideell förening
Adressändring ideell förening Blomman för dagen drog
Blomman för dagen drog Borra hål för knoppar
Borra hål för knoppar Bris för vuxna
Bris för vuxna Bra mat för unga idrottare
Bra mat för unga idrottare Smärtskolan kunskap för livet
Smärtskolan kunskap för livet Frgar
Frgar Vad är ett minoritetsspråk
Vad är ett minoritetsspråk Ledarskapsteorier
Ledarskapsteorier Datorkunskap för nybörjare
Datorkunskap för nybörjare Humanitr
Humanitr Vad står k.r.å.k.a.n för
Vad står k.r.å.k.a.n för Steg för steg rita
Steg för steg rita Redogör för vad psykologi är
Redogör för vad psykologi är Claes martinsson
Claes martinsson Gumman cirkel sång
Gumman cirkel sång Offentlig förvaltning
Offentlig förvaltning Klassens frågetecken rim
Klassens frågetecken rim Nyckelkompetenser för livslångt lärande
Nyckelkompetenser för livslångt lärande