TwoSample Inference Procedures with Means TwoSample Procedures with








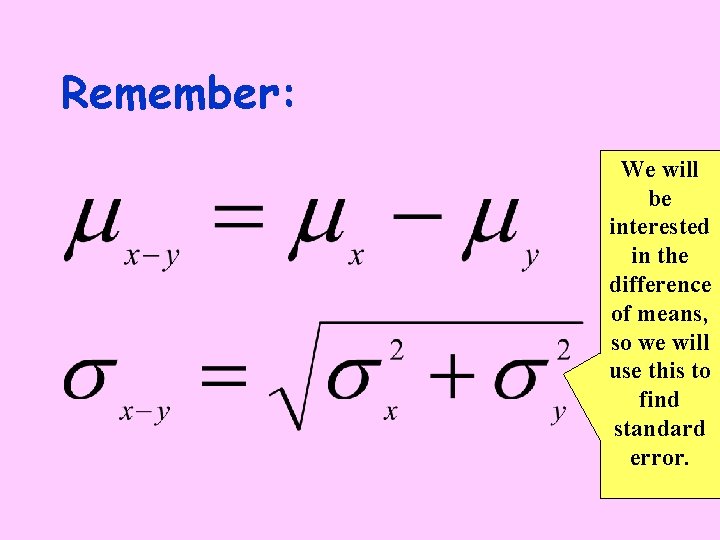



























- Slides: 39

Two-Sample Inference Procedures with Means

Two-Sample Procedures with means • The goal of these inference procedures is to compare the responses to two treatments or to compare the characteristics of two populations • We have INDEPENDENT samples from each treatment or population

Assumptions: • Have two SRS’s from the populations or two randomly assigned treatment groups • Samples are independent • Both distributions are approximately normally – Have large sample sizes – Graph BOTH sets of data • s’s known/unknown

Note: confidence interval statements • Matched pairs – refer to “mean difference” • Two-Sample – refer to “difference of means”

Hypothesis Statements: H 0 : m 1 = - m 2 = 0 Ha : H Haa: : m 1<- mm 22 < 0 m 1>- mm 22 > 0 mm 11 -≠ mm 22 ≠ 0 Be sure to define BOTH m 1 and m 2!

Hypothesis Test: Since we usually assume H 0 is true, then this equals 0 – so we can usually leave it out

Hypothesis statements: H 0 : p 1 = p 2 H 0: p 1 - p 2 = 0 Ha : p 1 > p 2 H a : p 1 - p 2 > 0 Ha : p 1 < p 2 H a : p 1 - p 2 < 0 Ha : p 1 ≠ p 2 H a : p 1 - p 2 ≠ 0 Be sure to define both p 1 & p 2!

Formula for Hypothesis test: Usually p 1 – p 2 =0
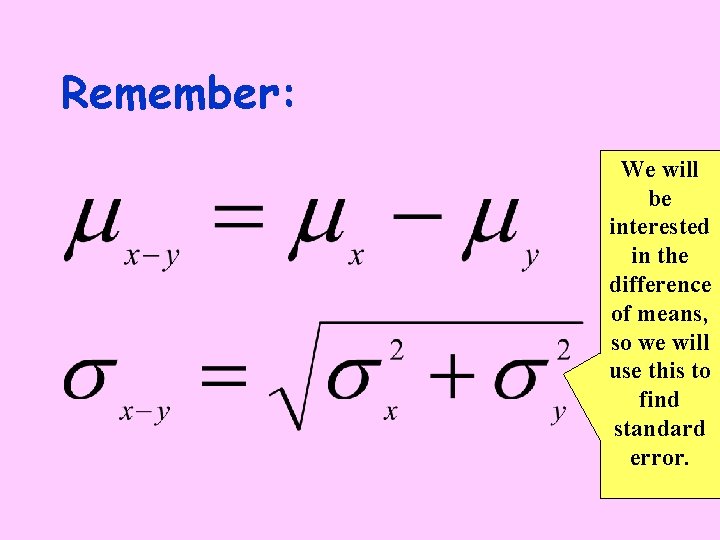
Remember: We will be interested in the difference of means, so we will use this to find standard error.

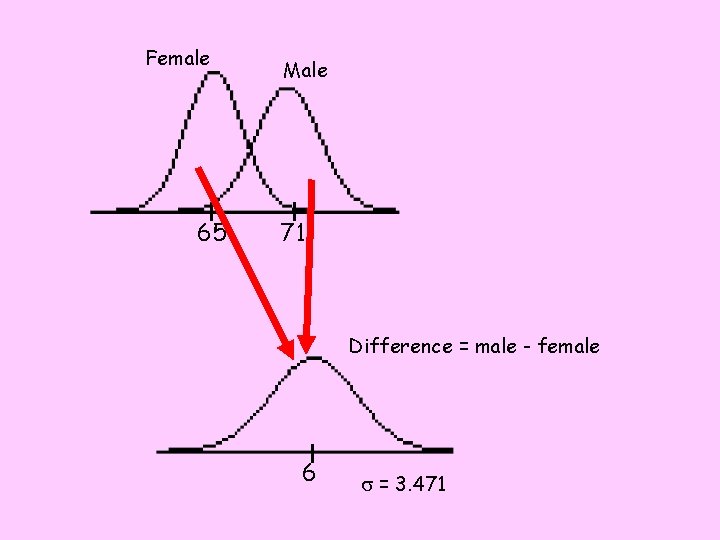
Suppose we have a population of adult men with a mean height of 71 inches and standard deviation of 2. 6 inches. We also have a population of adult women with a mean height of 65 inches and standard deviation of 2. 3 inches. Assume heights are normally distributed. Describe the distribution of the difference in heights between males and females (malefemale). Normal distribution with mx-y =6 inches & sx-y =3. 471 inches

Female 65 Male 71 Difference = male - female 6 s = 3. 471

a) What is the probability that the height of a randomly selected man is at most 5 inches taller than the height of a randomly selected woman? P((x. M-x. F) < 5) = normalcdf(-∞, 5, 6, 3. 471) =. 3866 b) What is the 70 th percentile for the difference (male-female) in heights of a randomly selected man & woman? (x. M-x. F) = inv. Norm(. 7, 6, 3. 471) = 7. 82

Formulas Since in real-life, we will NOT know both s’s, we will do t-procedures.

Degrees of Freedom Option 1: use the smaller of the two values n 1 – 1 and n 2 – 1 This will produce conservative results – higher p-values & lower confidence. Calculator Option 2: approximation used bydoes this automatically! technology

Confidence Called intervals: standard error

Pooled procedures: • Used for two populations with the same variance • When you pool, you average the two -sample variances to estimate the common population variance. • DO NOT use on AP Exam!!!!! We do NOT know the variances of the population, so ALWAYS tell the calculator NO for pooling!

Two competing headache remedies claim to give fastacting relief. An experiment was performed to compare the mean lengths of time required for bodily absorption of brand A and brand B. Assume the absorption time is normally distributed. Twelve people were randomly selected and given an oral dosage of brand A. Another 12 were randomly selected and given an equal dosage of brand B. The length of time in minutes for the drugs to reach a specified level in the blood was recorded. The results follow: mean SD n Brand A 20. 1 8. 7 12 Brand B 18. 9 7. 5 12 Describe the shape & standard error for sampling distribution of the differences in the mean speed of absorption. (answer on next screen)

Describe the sampling distribution of the differences in the mean speed of absorption. Normal distribution with S. E. = 3. 316 Find a 95% confidence interval difference in mean lengths of time required for bodily absorption of each brand. (answer on next screen)

Assumptions: Have 2 independent randomly assigned treatments Given the absorption rate is normally distributed s’s unknown From calculator df = We are 95% confident that the true difference in mean 21. 53, use t* for df = lengths of time required for bodily absorption of each 21 & 95% confidence brand is between – 5. 685 minutes and 8. 085 minutes. level

The length of time in minutes for the drugs to reach a specified level in the blood was recorded. The results follow: Brand A Brand B mean 20. 1 18. 9 SD 8. 7 7. 5 n 12 12 Is there sufficient evidence that these drugs differ in the speed at which they enter the blood stream?

Have 2 independent randomly assigned treatments State assumptions! Given the absorption rate is normally distributed s’s unknown H 0: m. A= m. B Ha: m. A= m. B Hypotheses & define variables! Where m. A is the true mean absorption time for Brand A & m. B is the true mean absorption time for Brand B Formula & calculations Conclusion in context Since p-value > a, I fail to reject H 0. There is not sufficient evidence to suggest that these drugs differ in the speed at which they enter the blood stream.

Suppose that the sample mean of Brand B is 16. 5, then is Brand B faster? No, I would still fail to reject the null hypothesis.

Robustness: • Two-sample procedures are more robust than one-sample procedures • BEST to have equal sample sizes! (but not necessary)

A modification has been made to the process for producing a certain type of time-zero film (film that begins to develop as soon as the picture is taken). Because the modification involves extra cost, it will be incorporated only if sample data indicate that the modification decreases true average development time by more than 1 second. Should the company incorporate the modification? Original 8. 6 5. 1 4. 5 5. 4 Modified 5. 5 4. 0 3. 8 6. 0 6. 3 6. 6 5. 8 4. 9 5. 7 8. 5 7. 0 5. 7

Assume we have 2 independent SRS of film Both distributions are approximately normal due to approximately symmetrical boxplots s’s unknown H 0: m. O- m. M = 1 Ha: m. O- m. M > 1 Where m. O is the true mean developing time for original film & m. M is the true mean developing time for modified film Since p-value > a, I fail to reject H 0. There is not sufficient evidence to suggest that the company incorporate the modification.

Two-Sample Proportions Inference

Assumptions: • Two, Two independent SRS’s from populations ( or randomly assigned treatments) • Populations at least 10 n • Normal approximation for both

Sampling Distributions for the difference in proportions When tossing pennies, the probability of the coin landing on heads is 0. 5. However, when spinning the coin, the probability of the coin landing on heads is 0. 4. Assume 25 trials were completed

Looking at the sampling distribution of the difference in sample proportions: What is the mean of the difference in sample proportions (flip - spin)? Can the sampling distribution of difference in sample proportions (flip spin) be approximated by a normal distribution? What is the probability that the difference in proportions (flipped – spun) is at least. 25? Yes, since n 1 p 1=12. 5, n 1(1 -p 1)=12. 5, n 2 p 2=10, n 2(1 -p 2)=15 – so all are at least 5)

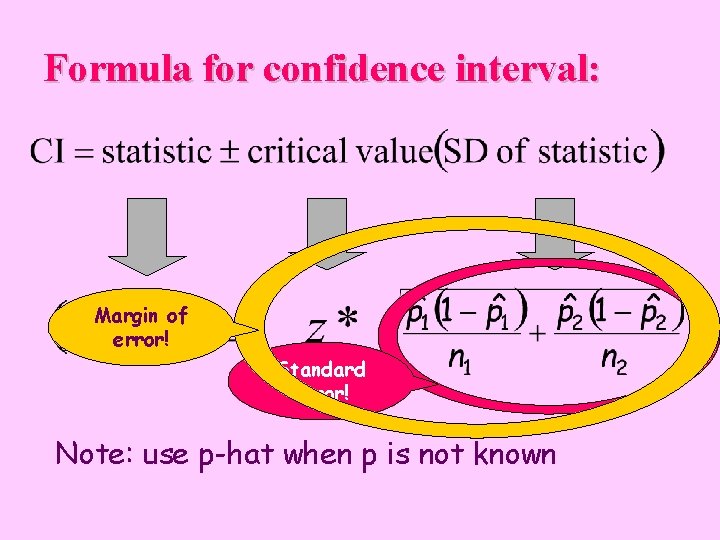
Formula for confidence interval: Margin of error! Standard error! Note: use p-hat when p is not known

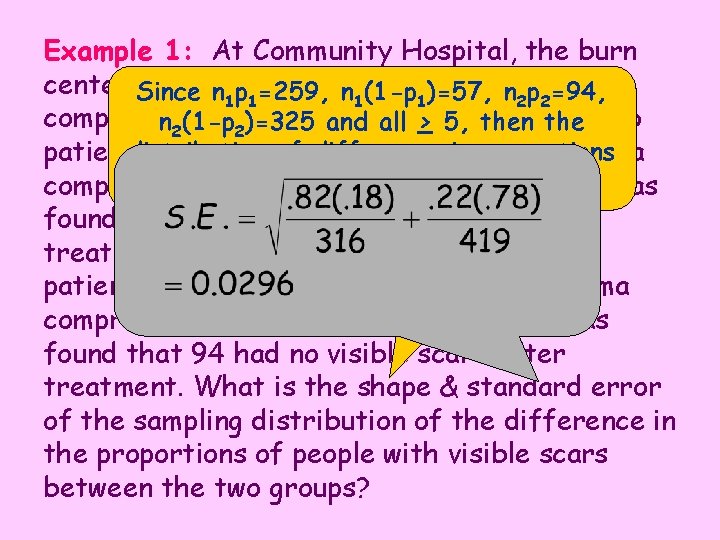
Example 1: At Community Hospital, the burn center Since is experimenting new nplasma n 1 p 1=259, n 1 with (1 -p 1 a )=57, 2 p 2=94, compressn 2 treatment. A random of 316 (1 -p 2)=325 and all > 5, sample then the distribution of burns difference in proportions patients with minor received the plasma is approximately normal. compress treatment. Of these patients, it was found that 259 had no visible scars after treatment. Another random sample of 419 patients with minor burns received no plasma compress treatment. For this group, it was found that 94 had no visible scars after treatment. What is the shape & standard error of the sampling distribution of the difference in the proportions of people with visible scars between the two groups?

Example 1: At Community Hospital, the burn center is experimenting with a new plasma compress treatment. A random sample of 316 patients with minor burns received the plasma compress treatment. Of these patients, it was found that 259 had no visible scars after treatment. Another random sample of 419 patients with minor burns received no plasma compress treatment. For this group, it was found that 94 had no visible scars after treatment. What is a 95% confidence interval of the difference in proportion of people who had no visible scars between the plasma compress treatment & control group?

Assumptions: Since these are all burn patients, we can add 316 + 419 treatment = 735. • Have 2 independent randomly assigned groups If not the same – you MUST list separately. • Both distributions are approximately normal since n 1 p 1=259, n 1(1 -p 1)=57, n 2 p 2=94, n 2(1 -p 2)=325 and all > 5 • Population of burn patients is at least 7350. We are 95% confident that the true the difference in proportion of people who had no visible scars between the plasma compress treatment & control group is between 53. 7% and 65. 4%

Example 2: Suppose that researchers want to estimate the difference in proportions of people who are against the death penalty in Texas & in Since both n’s are the same California. size, Ifyou the two sample sizes have common denominators so add! are the same, what –size sample is needed to be within 2% of the true difference at 90% confidence? n = 3383

Example Researchers comparing the effectiveness of SO 3: – which is correct? two pain medications randomly selected a group of patients who had been complaining of a certain kind of CIA = divided (. 67, . 83) joint pain. They randomly these people into two CIB =(. 52, the. 70) groups, and then administered painkillers. Of the 112 Since intervals overlap, it appears that people in thethe group who received medication A, 84 said there is no was difference in Of thethe proportion ofin the this pain reliever effective. 108 people 66 who reported other group, reported thatpainrelieverbetween B was effective. (BVD, p. the 435)two medicines. a) Construct separate 95% confidence intervals for the CI = who (0. 017, 0. 261) proportion of people reported that the pain reliever zero Based is not on in these the interval, was Since effective. intervals there how doisthe a difference in who the reported proportion ofrelieve peoplewith proportions of people pain who reported pain relieve between the medication A or medication B compare? medicines. b) Construct a 95%two confidence interval for the difference in the proportions of people who may find these medications effective.

Since we assume that the population proportions are equal in the null hypothesis, the variances are equal. Therefore, we pool the variances! Do not do on AP exam!!!

Formula for Hypothesis test: Usually p 1 – p 2 =0

Example 4: A forest in Oregon has an infestation of spruce moths. In an effort to control the moth, one area has been regularly sprayed from airplanes. In this area, a random sample of 495 spruce trees showed that 81 had been killed by moths. A second nearby area receives no treatment. In this area, a random sample of 518 spruce trees showed that 92 had been killed by the moth. Do these data indicate that the proportion of spruce trees killed by the moth is different for these areas?

Assumptions: • Have 2 independent SRS of spruce trees • Both distributions are approximately normal since n 1 p 1=81, n 1(1 -p 1)=414, n 2 p 2=92, n 2(1 -p 2)=426 and all > 5 • Population of spruce trees is at least 10, 130. H 0: p 1=p 2 Ha: p 1≠p 2 where p 1 is the true proportion of trees killed by moths in the treated area p 2 is the true proportion of trees killed by moths in the untreated area P-value = 0. 5547 a = 0. 05 Since p-value > a, I fail to reject H 0. There is not sufficient evidence to suggest that the proportion of spruce trees killed by the moth is different for these areas
 Meta means change and morph means heat
Meta means change and morph means heat Definition of biodiversity conservation
Definition of biodiversity conservation Triangle quadrilateral pentagon hexagon
Triangle quadrilateral pentagon hexagon Bio means 'life
Bio means 'life Metamorphic rocks
Metamorphic rocks Unrestricted
Unrestricted Causal inference ai
Causal inference ai Observation vs inference
Observation vs inference Deduction and inference
Deduction and inference How does textual evidence help a reader make an inference
How does textual evidence help a reader make an inference Fact inference confusion examples
Fact inference confusion examples Inference
Inference Inference for a single proportion
Inference for a single proportion Vipers skills
Vipers skills Theory based inference applet
Theory based inference applet Magnitude-based inference
Magnitude-based inference Contoh kalimat inference
Contoh kalimat inference Diagnostic cast
Diagnostic cast Statistical inference is divided into
Statistical inference is divided into Multiple regression analysis inference
Multiple regression analysis inference What is inference in reading
What is inference in reading Proof by contradiction examples
Proof by contradiction examples Expérience de asch 1946
Expérience de asch 1946 Inference examples for students
Inference examples for students Incredible sentence
Incredible sentence At four hundred miles they stopped to eat
At four hundred miles they stopped to eat Active inference
Active inference Resolution in fol
Resolution in fol Fuzzy inference system
Fuzzy inference system Guided reading inference
Guided reading inference Making an inference
Making an inference Active inference
Active inference Rules of inference
Rules of inference Inference by enumeration in artificial intelligence
Inference by enumeration in artificial intelligence Inference in database security
Inference in database security The man loves to garden outside inference
The man loves to garden outside inference Inference by enumeration in artificial intelligence
Inference by enumeration in artificial intelligence Inference objectives
Inference objectives What is inference in pragmatics with examples
What is inference in pragmatics with examples Gunnar taraldsen
Gunnar taraldsen