Chapter 10 TwoSample Tests TwoSample Tests Population Means

Chapter 10 Two-Sample Tests

Two-Sample Tests Population Means, Independent Samples Population Means, Related Samples Population Proportions Population Variances Examples: Group 1 vs. Group 2 Same group before vs. after treatment Proportion 1 vs. Proportion 2 Variance 1 vs. Variance 2

Difference Between Two Means: Independent Samples Population means, independent samples n * σ1 and σ2 unknown, assumed equal σ1 and σ2 unknown, not assumed equal Different data sources n n Unrelated Independent n Sample selected from one population has no effect on the sample selected from the other population Use Sp to estimate unknown σ. Use a Pooled-Variance t test. Use S 1 and S 2 to estimate unknown σ1 and σ2. Use a Separate-variance t test

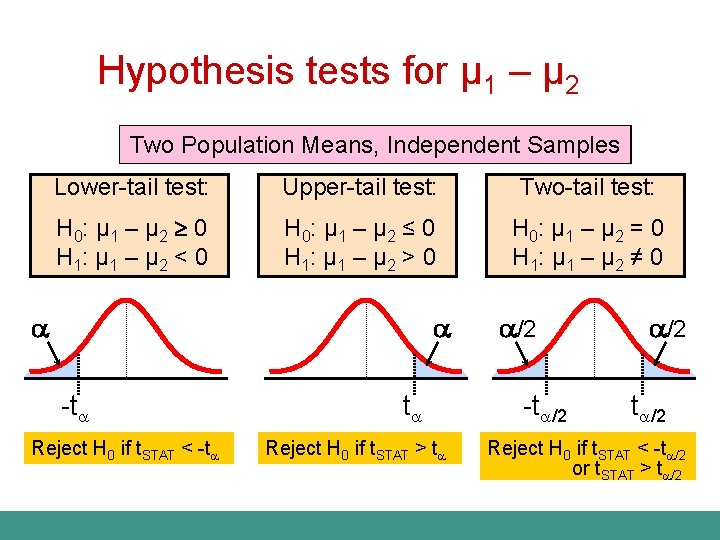
Hypothesis tests for μ 1 – μ 2 Two Population Means, Independent Samples Lower-tail test: Upper-tail test: Two-tail test: H 0: μ 1 – μ 2 0 H 1: μ 1 – μ 2 < 0 H 0: μ 1 – μ 2 ≤ 0 H 1: μ 1 – μ 2 > 0 H 0: μ 1 – μ 2 = 0 H 1: μ 1 – μ 2 ≠ 0 -t Reject H 0 if t. STAT < -t t Reject H 0 if t. STAT > t /2 -t /2 Reject H 0 if t. STAT < -t /2 or t. STAT > t /2

Hypothesis tests for µ 1 - µ 2 with σ1 and σ2 unknown and assumed equal • The pooled variance is: Population means, independent samples σ1 and σ2 unknown, assumed equal σ1 and σ2 unknown, not assumed equal * • The test statistic is: • Where t. STAT has d. f. = (n 1 + n 2 – 2)

Pooled-Variance t Test Example You are a financial analyst for a brokerage firm. Is there a difference in dividend yield between stocks listed on the NYSE & NASDAQ? You collect the following data: NYSE NASDAQ Number 21 25 Sample mean 3. 27 2. 53 Sample std dev 1. 30 1. 16 Assuming both populations are approximately normal with equal variances, is there a difference in mean yield ( = 0. 05)?

Pooled-Variance t Test Example: Calculating the Test Statistic H 0: μ 1 - μ 2 = 0 i. e. (μ 1 = μ 2) H 1: μ 1 - μ 2 ≠ 0 i. e. (μ 1 ≠ μ 2) The test statistic is:

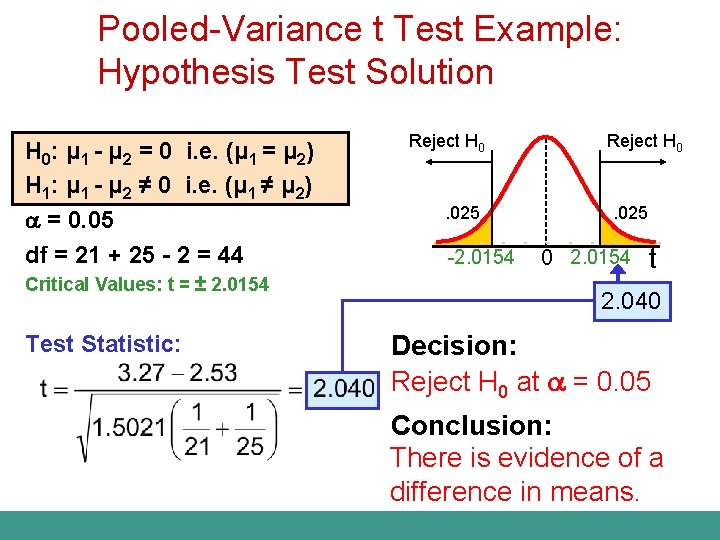
Pooled-Variance t Test Example: Hypothesis Test Solution H 0: μ 1 - μ 2 = 0 i. e. (μ 1 = μ 2) H 1: μ 1 - μ 2 ≠ 0 i. e. (μ 1 ≠ μ 2) = 0. 05 df = 21 + 25 - 2 = 44 Critical Values: t = ± 2. 0154 Test Statistic: Reject H 0 . 025 -2. 0154 Reject H 0 . 025 0 2. 0154 t 2. 040 Decision: Reject H 0 at = 0. 05 Conclusion: There is evidence of a difference in means.

Pooled Variance T-Test, page 350 n Open Two-Sample Tests Excel file on Oncourse n n n All sample calculations have been provided, excel functions are next to values In cell B 16 type B 7 -1 In cell B 17 type B 11 – 1 In cell B 18 type B 16 + B 17 In cell B 19 type = ((B 16 * B 9^2) + (B 17*B 13^2))/B 18 In cell B 20 type = Sqrt(B 19*(1/B 7 +1/B 11) In cell B 21 type = B 8 – B 12 In cell B 22 type = (B 21 – B 4)/B 20 In cell B 25 type = -tinv(B 5, B 18) In cell B 26 type = tinv(B 5, B 18) In cell B 27 type = TDIST(ABS(B 22), B 18, 2) In cell B 28 type = IF(B 27<B 5, “Reject the null hypothesis”, “Do not reject the null hypothesis”)

Hypothesis tests for µ 1 - µ 2 with σ1 and σ2 unknown and not assumed equal Population means, independent samples σ1 and σ2 unknown, assumed equal σ1 and σ2 unknown, not assumed equal The test statistic is: t. STAT has d. f. ν = *

Separate-Variance t Test Example You are a financial analyst for a brokerage firm. Is there a difference in dividend yield between stocks listed on the NYSE & NASDAQ? You collect the following data: NYSE NASDAQ Number 21 25 Sample mean 3. 27 2. 53 Sample std dev 1. 30 1. 16 Assuming both populations are approximately normal with unequal variances, is there a difference in mean yield ( = 0. 05)?

Separate-Variance t Test Example: Calculating the Test Statistic H 0: μ 1 - μ 2 = 0 i. e. (μ 1 = μ 2) H 1: μ 1 - μ 2 ≠ 0 i. e. (μ 1 ≠ μ 2) The test statistic is: Use degrees of freedom = 40

Separate-Variance t Test Example: Hypothesis Test Solution H 0: μ 1 - μ 2 = 0 i. e. (μ 1 = μ 2) H 1: μ 1 - μ 2 ≠ 0 i. e. (μ 1 ≠ μ 2) = 0. 05 df = 40 Critical Values: t = ± 2. 021 Test Statistic: Reject H 0 . 025 -2. 021 Reject H 0 . 025 0 2. 021 2. 019 t Decision: Fail To Reject H 0 at = 0. 05 Conclusion: There is insufficient evidence of a difference in means.

Unequal Variance (using same data as pooled variance), page 356 n n n n In cell B 16 type =B 9^2 In cell B 17 type =B 13^2 In cell B 18 type =B 16/B 7 In cell B 19 type =B 17/B 11 In cell B 20 type =(B 18+B 19)^2 In cell B 21 type =(B 18^2)/(B 7 -1)+(B 19^2)/(B 11 -1) In cell B 22 type = B 20/B 21 In cell B 23 type = INT(B 22) In cell B 24 type = =SQRT(B 18+B 19) In cell B 25 type = =B 8 -B 12 In cell B 26 type = =(B 25 -B 4)/B 24 In cell B 29 type = -tinv(B 5, B 23) In cell B 30 type = tinv(B 5, B 23) In cell B 31 type = TDIST(ABS(B 22), B 19, 2) In cell B 32 type = IF(B 27<B 5, “Reject the null hypothesis”, “Do not reject the null hypothesis”)

Related Populations The Paired Difference Tests Means of 2 Related Populations Related samples n n n Paired or matched samples Repeated measures (before/after) Use difference between paired values: Di = X 1 i - X 2 i n n Eliminates Variation Among Subjects Assumptions: n Both Populations Are Normally Distributed n Or, if not Normal, use large samples

Related Populations The Paired Difference Test The ith paired difference is Di , where Related samples Di = X 1 i - X 2 i The point estimate for the paired difference population mean μD is D : The sample standard deviation is SD n is the number of pairs in the paired sample

The Paired Difference Test: Finding t. STAT Paired samples n The test statistic for μD is: n Where t. STAT has n - 1 d. f.

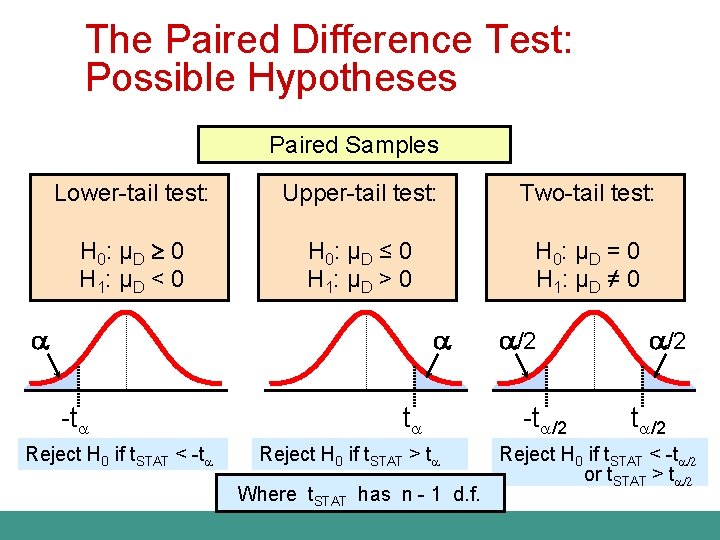
The Paired Difference Test: Possible Hypotheses Paired Samples Lower-tail test: Upper-tail test: Two-tail test: H 0: μ D 0 H 1: μ D < 0 H 0: μ D ≤ 0 H 1: μ D > 0 H 0: μ D = 0 H 1: μ D ≠ 0 -t Reject H 0 if t. STAT < -t t Reject H 0 if t. STAT > t Where t. STAT has n - 1 d. f. /2 -t /2 Reject H 0 if t. STAT < -t /2 or t. STAT > t /2

Paired Difference Test: Example Assume you send your salespeople to a “customer service” training workshop. Has the training made a difference in the number of complaints? You collect the following data: n Number of Complaints: (2) - (1) Salesperson Before (1) After (2) Difference, Di C. B. T. F. M. H. R. K. M. O. 6 20 3 0 4 4 6 2 0 0 - 2 -14 - 1 0 - 4 -21 D = Di n = -4. 2

Paired Difference Test: Solution n Has the training made a difference in the number of complaints (at the 0. 01 level)? H 0: μ D = 0 H 1: μD 0 =. 01 D = - 4. 2 t 0. 005 = ± 4. 604 d. f. = n - 1 = 4 Test Statistic: Reject /2 - 4. 604 - 1. 66 4. 604 Decision: Do not reject H 0 (tstat is not in the reject region) Conclusion: There is not a significant change in the number of complaints.

Paired T-Test (Mean and Standard Deviation), page 361 n n In Cell E 2 type = C 2 – D 2, drag through E 17 In Cell F 2 type = (E 2 - $B$22)^2, draft through F 17

Paired T-Test (Calculations), page 361 n n n n n In cell B 8 type your n-value (16) In cell B 9 type = AVERAGE('Paired t Test (Mean & St Dev)'!E 2: E 17) In cell B 10 type = B 8 -1 In Cell B 11, type = SQRT(SUM('Paired t Test (Mean & St Dev)'!F 2: F 17)/('Paired t Test (Calculations)'!B 8 -1)) In cell B 12 type = B 11/sqrt(B 8) In cell B 13 type = (B 9 – B 4)/B 12 In cell B 16 type = -tinv(B 5, B 10) In cell B 17 type = tinv(B 5, B 10) In cell B 18 type = TDIST(ABS(B 13), B 10, 2) In cell B 19 type = IF(B 18<B 5, “Reject the null hypothesis”, “Do not reject the null hypothesis”)

Two Population Proportions Population proportions Goal: test a hypothesis or form a confidence interval for the difference between two population proportions, π1 – π2 Assumptions: n 1 π1 5 , n 1(1 - π1) 5 n 2 π2 5 , n 2(1 - π2) 5 The point estimate for the difference is

Two Population Proportions Population proportions In the null hypothesis we assume the null hypothesis is true, so we assume π1 = π2 and pool the two sample estimates The pooled estimate for the overall proportion is: where X 1 and X 2 are the number of items of interest in samples 1 and 2

Two Population Proportions The test statistic for π1 – π2 is a Z statistic: Population proportions where

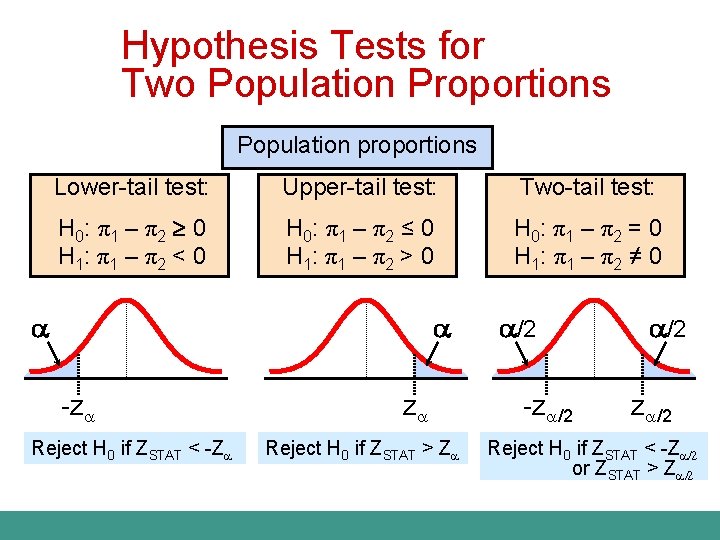
Hypothesis Tests for Two Population Proportions Population proportions Lower-tail test: Upper-tail test: Two-tail test: H 0: π 1 – π 2 0 H 1: π 1 – π 2 < 0 H 0: π 1 – π 2 ≤ 0 H 1: π 1 – π 2 > 0 H 0: π 1 – π 2 = 0 H 1: π 1 – π 2 ≠ 0 -z Reject H 0 if ZSTAT < -Z z Reject H 0 if ZSTAT > Z /2 -z /2 Reject H 0 if ZSTAT < -Z /2 or ZSTAT > Z /2

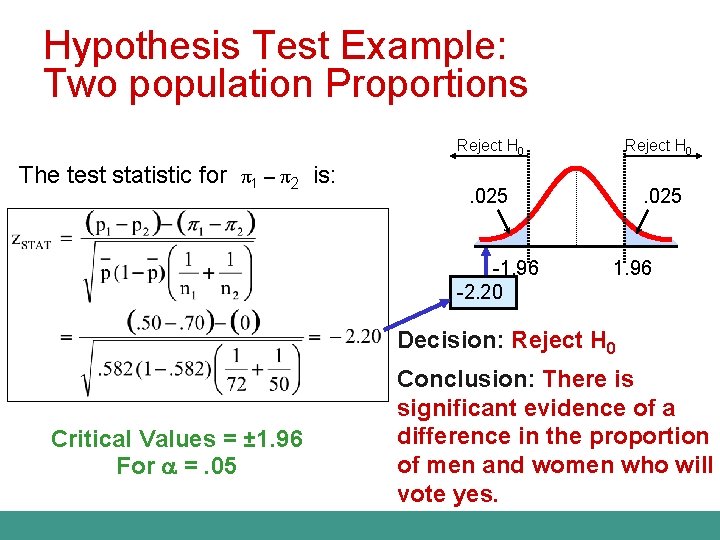
Hypothesis Test Example: Two population Proportions Is there a significant difference between the proportion of men and the proportion of women who will vote Yes on Proposition A? n n In a random sample, 36 of 72 men and 35 of 50 women indicated they would vote Yes Test at the. 05 level of significance

Hypothesis Test Example: Two population Proportions n The hypothesis test is: H 0: π1 – π2 = 0 (the two proportions are equal) H 1: π1 – π2 ≠ 0 (there is a significant difference between proportions) n The sample proportions are: n Men: p 1 = 36/72 = 0. 50 n Women: p 2 = 35/50 = 0. 70 § The pooled estimate for the overall proportion is:

Hypothesis Test Example: Two population Proportions The test statistic for π1 – π2 is: Reject H 0 . 025 -1. 96 -2. 20 1. 96 Decision: Reject H 0 Critical Values = ± 1. 96 For =. 05 Conclusion: There is significant evidence of a difference in the proportion of men and women who will vote yes.

Z-Test for Two Proportions, page 370 n n n n n In cell B 14 type = B 7/B 8 In cell B 15 type = B 10/B 11 In cell B 16 type = B 14 – B 15 In cell B 17 type = (B 7 + B 10)/(B 8 + B 11) In cell B 18 type = (B 16 – B 4)/sqrt(B 7*(1 -B 7)*(1/B 8 + 1/B 11)) In cell B 21 type = normsinv(B 5/2) In cell B 22 type = normsinv(1 -B 5/2) In cell B 23 type = 2*(1 – normsdist(ABS(B 18))) In cell B 24 type = IF(B 23<B 5, “Reject the null hypothesis”, “Do not reject the null hypothesis”)

Testing for the Ratio Of Two Population Variances Tests for Two Population Variances F test statistic * Hypotheses H 0: σ 12 = σ 22 H 1: σ 12 ≠ σ 22 H 0: σ 12 ≤ σ 22 H 1: σ 12 > σ 22 FSTAT S 12 / S 22 Where: S 12 = Variance of sample 1 (the larger sample variance) n 1 = sample size of sample 1 S 22 = Variance of sample 2 (the smaller sample variance) n 2 = sample size of sample 2 n 1 – 1 = numerator degrees of freedom n 2 – 1 = denominator degrees of freedom

The F Distribution n n The F critical value is found from the F table There are two degrees of freedom required: numerator and denominator n The larger sample variance is always the numerator n When n In the F table, df 1 = n 1 – 1 ; df 2 = n 2 – 1 n numerator degrees of freedom determine the column n denominator degrees of freedom determine the row

Finding the Rejection Region H 0: σ 12 = σ 22 H 1: σ 12 ≠ σ 22 H 0: σ 12 ≤ σ 22 H 1: σ 12 > σ 22 /2 0 Do not reject H 0 Fα/2 Reject H 0 if FSTAT > Fα/2 F 0 Do not reject H 0 Fα Reject H 0 if FSTAT > Fα F

F Test: An Example You are a financial analyst for a brokerage firm. You want to compare dividend yields between stocks listed on the NYSE & NASDAQ. You collect the following data: NYSE NASDAQ Number 21 25 Mean 3. 27 2. 53 Std dev 1. 30 1. 16 Is there a difference in the NYSE 0. 05 level? variances between & NASDAQ at the =

F Test: Example Solution n DCOVA Form the hypothesis test: H 0: σ21 = σ22 (there is no difference between variances) H 1: σ21 ≠ σ22 (there is a difference between variances) n Find the F critical value for = 0. 05: n Numerator d. f. = n 1 – 1 = 21 – 1 =20 n Denominator d. f. = n 2 – 1 = 25 – 1 = 24 n Fα/2 = F. 025, 20, 24 = 2. 33

F Test: Example Solution DCOVA (continued) n The test statistic is: H 0 : σ1 2 = σ2 2 H 1 : σ1 2 ≠ σ2 2 /2 =. 025 0 n n FSTAT = 1. 256 is not in the rejection region, so we do not reject H 0 Do not reject H 0 Conclusion: There is not sufficient evidence of a difference in variances at =. 05 Reject H 0 F 0. 025=2. 33 F

F Test for Ratio of Two Variances (using same data as pooled variance), page 376 n n n In cell B 13 type = B 7/B 10 In cell B 14 type = B 6 -1 In cell B 15 type = B 9 - 1 In cell B 18 type = FINV(B 4/2, B 14, B 15) In cell B 19 type = 2*FDIST(B 13, B 14, B 15) In cell B 20 type = IF(B 19<B 4, “Reject the null hypothesis”, “Do not reject the null hypothesis”)