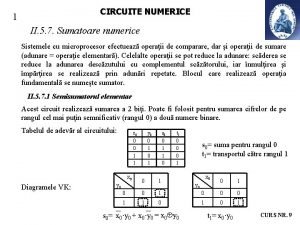
METODE NUMERICE DE SOLUIONARE A ECUAIILOR DIFERENIALE PREZENTARE

METODE NUMERICE DE SOLU|IONARE A ECUA|IILOR DIFEREN|IALE PREZENTARE GENERAL{

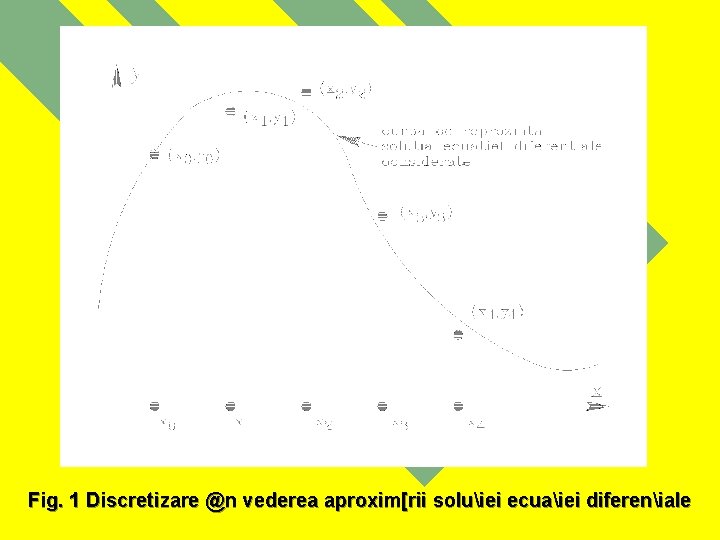
INTRODUCERE n O ecuaie diferenial[ poate s[ nu posede soluie sau, chiar dac[ are soluie, nu totdeauna aceasta se poate explicita. #n multe situaii, mai ales @n cazul ecuaiilor difereniale neliniare, trebuie s[ ne consider[m mulumii dac[ obinem o aproximaie a soluiei ecuaiei difereniale. #n cele ce urmeaz[, utiliz`nd metode numerice, se vor obine seturi de puncte care, atunci c`nd se utilizeaz[ discretiz[ri suficient de fine pot aproxima soluia ecuaiei difereniale considerate, a]a cum se prezint[ @n fig. 1.

Fig. 1 Discretizare @n vederea aproxim[rii soluiei ecuaiei difereniale

Se face meniunea c[ @n cadrul acestui capitol interesul va fi direcionat numai @nspre ecuaii difereniale de ordinul 1: dat fiind faptul c[ ecuaiile difereniale de ordin superior pot fi reduse la sisteme de ecuaii difereniale de ordinul 1.

#ntr-adev[r, consider`nd ecuaia diferenial[: (1) ]i introduc`nd variabilele: , (2) rezult[ c[: (3) #n acest fel ecuaia diferenial[ de ordinul n scris[ sub forma (1) se poate echivala cu urm[torul sistem de n ecuaii difereniale de ordinul 1:

METODA EULER Aceasta este una dintre cele mai simple tehnici de soluionare numeric[ a ecuaiilor difereniale, fiind cunoscut[ ]i sub denumirea de metoda tangentelor. Se consider[ ecuaia diferenial[ (inclusiv condiia iniial[ aferent[): (5)

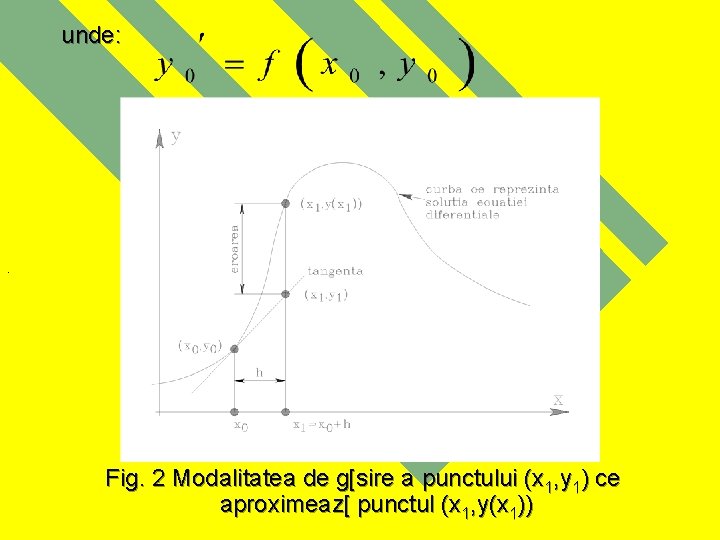
Dac[ se consider[ pe axa Ox o diviziune echidistant[ de pas h se poate g[si un punct ( x 1 , y 1 ) = ( x 0+h , y 1 ) pe tangenta la curba ce reprezint[ soluia ecuaiei difereniale @n punctul ( x 0 , y 0 ), a]a cum se prezint[ @n fig. 2. Se poate scrie: (6)

unde: . Fig. 2 Modalitatea de g[sire a punctului (x 1, y 1) ce aproximeaz[ punctul (x 1, y(x 1))

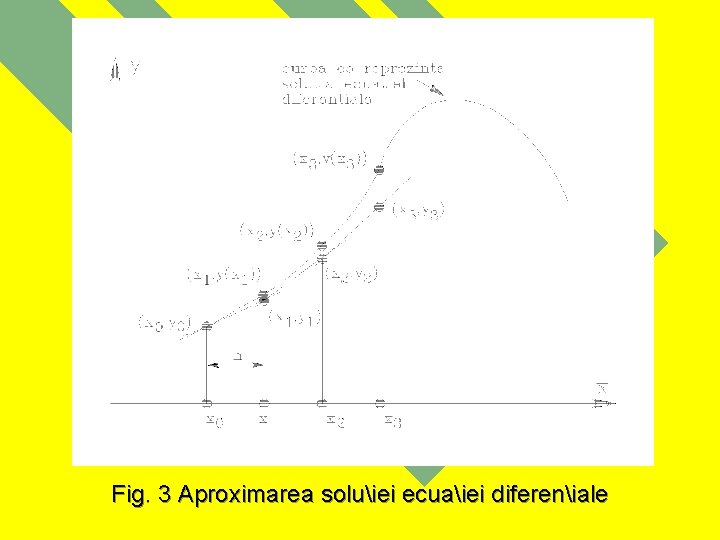
Fig. 3 Aproximarea soluiei ecuaiei difereniale

Dac[ se noteaz[ x 0+h = x 1, atunci punctul de coordonate ( x 1 , y 1 ) situat pe tangenta considerat[ reprezint[ a aproximaie a punctului de coordonate ( x 1 , y(x 1) ) situat pe curba ce reprezint[ soluia ecuaiei difereniale. Este evident faptul c[ eroarea metodei este cu at`t mai redus[ cu c`t valoarea pasului diviziunii considerate- h este mai mic. Se poate construi astfel un proces iterativ: (7) a c[rui reprezentare grafic[ se prezint[ @n fig. 3.

Exemplu Consider`nd ecuaia diferenial[: ]i condiia iniial[ y(1)=1, s[ se obin[ o aproximaie pentru a g[si valoarea lui y @n punctul de abscis[ x=1. 5, utiliz`nd un pa]i h cu valorile 0. 1, 0. 05 ]i 0. 01, apoi s[ se calculeze ]i erorile relative raportate la valoarea exact[, cu 4 zecimale. Soluie Soluia analitic[ a ecuaiei difereniale considerate este:

xn yn Exact Eroare % 1. 00 1. 10 1. 20 1. 30 1. 40 1. 50 1. 0000 1. 2000 1. 4640 1. 8154 2. 2874 2. 9278 1. 0000 1. 2337 1. 5527 1. 9937 2. 6117 3. 4904 0. 0000 0. 0337 0. 0887 0. 1784 0. 3244 0. 5625 0. 00 2. 73 5. 71 8. 95 12. 42 16. 12 Tab. 1 Valorile obinute pentru h=0. 1

xn yn Exact Eroare % 1. 00 1. 10 1. 20 1. 30 1. 40 1. 50 1. 0000 1. 2155 1. 5044 1. 8955 2. 4311 3. 1733 1. 0000 1. 2337 1. 5527 1. 9937 2. 6117 3. 4904 0. 0000 0. 0182 0. 0483 0. 0982 0. 1806 0. 3171 0. 00 1. 47 3. 11 4. 93 7. 98 9. 08 Tab. 2 Valorile obinute pentru h=0. 05

xn yn Exact Eroare % 1. 00 1. 10 1. 20 1. 30 1. 40 1. 50 1. 0000 1. 2298 1. 5423 1. 9723 2. 5719 3. 4197 1. 0000 1. 2337 1. 5527 1. 9937 2. 6117 3. 4904 0. 0000 0. 0039 0. 0104 0. 0214 0. 0398 0. 0707 0. 00 0. 31 0. 67 1. 07 1. 52 2. 03 Tab. 3 Valorile obinute pentru h=0. 01

#n continuare se prezint[ programul cu ajutorul c[ruia au fost obinute rezultatele numerice prezentate mai sus, realizat @n Turbo Pascal v. 7. 0. Program ED; var x 0, tfin, pas: real; i, nmax: integer; x, t: array[0. . 300] of real; fis: text; {Definirea ecuatiei diferentiale} Function eul 1(xe, te: real): real; begin eul 1: =2*xe*te; end;

begin Assign(fis, 'eul 3. dat'); Rewrite(fis); x 0: =1. 0; tfin: =1. 5; pas: =0. 01; nmax: =50; x[0]: =x 0; t[0]: =t 0; {Nume fisier} {Conditia initiala} {Intervalul de integrat} {Pasul de integrare} {Numarul de pasi}

for i: = 0 to nmax-1 do {Incepere proces iterativ} begin {metoda EULER} t[i+1]: =t[i]+pas; x[i+1]: =x[i]+pas*eul 1(x[i], t[i]); end; for i: = 0 to nmax do begin {Scriere fisier} writeln(fis, t[i]: 6: 2, ' ', x[i]: 6: 4); end; Close(fis); end.

METODA EULER-HEUN Aceast[ metod[ este cunoscut[ ]i sub denumirea de metoda Euler @mbun[t[it[, situaia fiind prezentat[ @n fig. 4 pentru primul pas de integrare. Procesul iterativ pentru soluionarea numeric[ este descris de relaia urm[toare: (8)

Fig. 4 Ilustrarea metodei Euler-Heun pentru primul interval al diviziunii considerate

Analiz`nd fig. 4 se poate constata c[ valoarea lui y 1 este mai apropiat[ de soluie dec`t valoarea obinut[ pentru y 1*, ceea ce poate @ncadra aceast[ metod[ @n clasa metodelor predictor-corector. #ntr-adev[r, aceast[ situaie se poate interpreta @n felul urm[tor: Pasul predictor

Pasul corector #n continuare, cu referire la ecuaia diferenial[ considerat[ anterior, se prezint[ rezultatele obinute prin aplicarea acestei metode pentru diferii pa]i de integrare ]i programul folosit pentru soluionarea numeric[.

xn yn Exact Eroare % 1. 00 1. 10 1. 20 1. 30 1. 40 1. 50 1. 0000 1. 2320 1. 5479 1. 9832 2. 5908 3. 4509 1. 0000 1. 2337 1. 5527 1. 9937 2. 6117 3. 4904 0. 0000 0. 0017 0. 0048 0. 0106 0. 0209 0. 0394 0. 00 0. 14 0. 31 0. 53 0. 80 1. 13 Tab. 4 Valorile obinute pentru h=0. 1

xn yn Exact Eroare % 1. 00 1. 10 1. 20 1. 30 1. 40 1. 50 1. 0000 1. 2332 1. 5514 1. 9909 2. 6060 3. 4795 1. 0000 1. 2337 1. 5527 1. 9937 2. 6117 3. 4904 0. 0000 0. 0004 0. 0013 0. 0029 0. 0057 0. 0108 0. 00 0. 04 0. 08 0. 14 0. 22 0. 31 Tab. 5 Valorile obinute pentru h=0. 05

xn yn Exact Eroare % 1. 00 1. 10 1. 20 1. 30 1. 40 1. 50 1. 0000 1. 2337 1. 5527 1. 9936 2. 6115 3. 4899 1. 0000 1. 2337 1. 5527 1. 9937 2. 6117 3. 4904 0. 0000 0. 0001 0. 0002 0. 0005 0. 005 0. 010 0. 025 Tab. 6 Valorile obinute pentru h=0. 01

Program ED; var x 0, tfin, pas: real; i, nmax: integer; x, t: array[0. . 300] of real; fis: text; {Definirea ecuatiei diferentiale} Function eul 1(xe, te: real): real; begin eul 1: =2*xe*te; end;

begin Assign(fis, 'heu 3. dat'); {Nume fisier} Rewrite(fis); x 0: =1. 0; {Conditia initiala} t 0: =1. 0; tfin: =1. 5; {Intervalul de integrat} pas: =0. 01; {Pasul de integrare} nmax: =50; {Numarul de pasi} x[0]: =x 0; t[0]: =t 0;

for i: = 0 to nmax-1 do {Incepere proces iterativ} begin {metoda EULER-HEUN} t[i+1]: =t[i]+pas; x[i+1]: =x[i]+pas*eul 1(x[i], t[i])/2+pas*eul 1(x[i]+ pas*eul 1(x[i], t[i]), t[i]+pas)/2; end; for i: = 0 to nmax do begin {Scriere fisier} writeln(fis, t[i]: 6: 2, ' ', x[i]: 6: 4); end; Close(fis); end.

METODA DEZVOLT{RII #N SERIE TAYLOR Aceast[ metod[ nu prezint[ o larg[ aplicabilitate deoarece, @n principal, rezultatele sunt comparabile cu cele obinute prin aplicarea metodei Euler-Heun @n condiiile unor calcule mai laborioase. A]a cum se ]tie, dezvoltarea unei funcii y(x) @n jurul unui punct x=a are expresia: (9)

Pentru a apropia forma (9) de problema curent[, dac[ se consider[ cazul @n care a=xn ]i x=xn+h, se obine: (10) Dac[ se presupune c[ funcia y(x) este soluia ecuaiei difereniale: (11)

Oprind numai doi termeni din (10) se poate scrie: (12)

Se observ[ faptul c[ dac[ @n (12) se @nlocuie]te y(xn+h) cu yn+1 ]i y(xn) cu yn se obine formula ce caracterizeaz[ metoda. Euler: (13)

Oprind trei termeni @n (10) ]i f[c`nd @nlocuirile antemenionate se obine urm[toarea formul[: (14) Metoda poate fi considerat[ drept cheia de bolt[ a majorit[ii metodelor de soluionare numeric[ a ecuaiilor difereniale.

METODE TIP RUNGE-KUTTA Aceast[ clas[ de metode reprezint[ una dintre cele mai folosite @n abordarea numeric[ a ecuaiilor difereniale, @mbin`nd num[rul relativ redus de operaii elementare cu acurateea rezultatelor. Metoda Runge-Kutta de ordinul II const[ @n g[sirea constantelor a, b, a, b astfel @nc`t expresia: (15)

cu: (16) s[ se apropie de dezvoltarea @n serie Taylor pentru c`t mai muli termeni posibili. Meritul principal al acestei clase de metode rezid[ deci @n aceea c[ se apropie de acurateea unei dezvolt[ri @n serie Taylor f[r[ @ns[ a fi nevoie s[ se calculeze ]i derivatele de ordin superior.

Se fac urm[toarele observaii: a) Dac[: atunci (15) reprezint[ dezvoltarea @n serie Taylor, oprind primii trei termeni, a funciei considerate.

b) Dac[: atunci (15) se reduce la expresia metodei Euler-Heun. c) Se poate constata c[ metoda Euler este de fapt o procedur[ Runge-Kutta de ordinul I.

Folosind acelea]i consideraii se determin[ astfel algoritmul de calcul ]i @n cazul metodei Runge-Kutta de ordinul IV (se opresc primii patru termeni din dezvoltarea @n serie Taylor): (17)

#n continuare se prezint[ rezultatele numerice obinute @n cazul aplic[rii acestei metode pentru rezolvarea ecuaiei difereniale considerate anterior ]i programul folosit @n acest scop. xn yn Exact Eroare % 1. 00 1. 10 1. 20 1. 30 1. 40 1. 50 1. 0000 1. 2337 1. 5527 1. 9937 2. 6116 3. 4902 1. 0000 1. 2337 1. 5527 1. 9937 2. 6117 3. 4904 0. 0000 0. 0001 0. 0002 0. 0038 0. 0076 Tab. 7 Valorile obinute pentru h=0. 1

xn yn Exact Eroare % 1. 00 1. 10 1. 20 1. 30 1. 40 1. 50 1. 0000 1. 2337 1. 5527 1. 9937 2. 6117 3. 4903 1. 0000 1. 2337 1. 5527 1. 9937 2. 6117 3. 4904 0. 0000 0. 0001 0. 0028 Tab. 8 Valorile obinute pentru h=0. 05

xn yn 1. 0000 1. 10 1. 2337 1. 20 1. 5527 1. 30 1. 9937 1. 40 2. 6117 1. 50 3. 4903429 Exact Eroare 1. 0000 0. 0000 1. 2337 0. 0000 1. 5527 0. 0000 1. 9937 0. 0000 2. 6117 0. 0000 3. 4904 0. 0000571 Eroare % 0. 0016 Tab. 9 Valorile obinute pentru h=0. 01

Program ED; var x 0, tfin, pas: real; i, nmax: integer; x, t, k 1, k 2, k 3, k 4: array[0. . 300] of real; fis: text; {Definirea ecuatiei diferentiale} Function eul 1(xe, te: real): real; begin eul 1: =2*xe*te; end;

begin Assign(fis, 'rk 43. dat'); {Nume fisier} Rewrite(fis); x 0: =1. 0; {Conditia initiala} t 0: =1. 0; tfin: =1. 5; {Intervalul de integrat} pas: =0. 01; {Pasul de integrare} nmax: =50; {Numarul de pasi} x[0]: =x 0; t[0]: =t 0;

for i: = 0 to nmax-1 do {Incepere proces iterativ} begin {metoda RUNGE-KUTTA IV} t[i+1]: =t[i]+pas; k 1[i]: =eul 1(x[i], t[i]); k 2[i]: =eul 1(x[i]+pas/2*k 1[i], t[i]+pas/2); k 3[i]: =eul 1(x[i]+pas/2*k 2[i], t[i]+pas/2); k 4[i]: =eul 1(x[i]+pas*k 3[i], t[i]+pas); x[i+1]: =x[i]+pas/6*(k 1[i]+2*k 2[i]+2*k 3[i]+k 4[i]); end;

for i: = 0 to nmax do begin {Scriere fisier} writeln(fis, t[i]: 6: 2, ' ', x[i]: 6: 4); end; Close(fis); end.

METODA MILNE Aceasta este o metod[ care lucreaz[ @n doi pa]i. Pasul predictor (18) unde:

(19)

Pasul corector (20) unde: (21)

Se remarc[ faptul c[ valorile pentru y 0, y 1, y 2 ]i y 3 trebuie cunoscute pentru demararea procesului iterativ. Acestea se pot calcula cu oricare dintre metodele anterioare, recomand`ndu-se @ns[ ca acest calcul iniial s[ se fac[ cu un nivel @nalt de acuratee.

CONCLUZII Aplicarea uneia sau alteia dintre aceste metode @n vederea soluion[rii unei probleme concrete implic[ o analiz[ atent[ a erorilor induse, @n vederea realiz[rii unui compromis acceptabil @ntre precizie ]i efortul de calcul cerut.