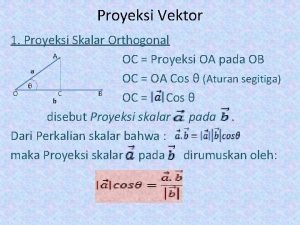
TEKNIK PROYEKSI BISNIS BAB 4 METODE PERAMALAN UNTUK

TEKNIK PROYEKSI BISNIS BAB 4 METODE PERAMALAN UNTUK MANAJEMEN Ardiprawiro S. E. , MMSI

TUJUAN PEMBELAJARAN Setelah mempelajari bab ini, Anda diharapkan dapat: “Mampu menjelaskan mengenai model sederhana, model rata-rata, metode pemulusan dan eksponensial, keterbatasan dan kekuatan metode eksponensial serta kegunaan bagi manajemen” ardiprawiro. staff. gunadarma. ac. id

METODE PERAMALAN v Salah satu alat yang diperlukan oleh manajemen dan merupakan bagian integral dari proses pengambilan keputusan ialah metode peramalan. v Metode peramalan digunakan untuk mengukur atau menaksir keadaan di masa datang. v Menurut Saputro dan Asri (2000), berdasarkan jenis data ramalan yang disusun, peramalan dibedakan menjadi dua yaitu: a) Peramalan Kualitatif b) Peramalan Kuantitatif ardiprawiro. staff. gunadarma. ac. id

JENIS-JENIS PERAMALAN v Berdasarkan horizon waktu, peramalan dapat dikelompokkan dalam tiga bagian yaitu: 1. Peramalan jangka panjang, yaitu yang mencakup waktu lebih besar dari 18 bulan. Misalnya, peramalan yang diperlukan dalam kaitannya dengan penanaman modal, perencanaan fasilitas, dan perencanaan untuk kegiatan litbang. 2. Peramalan jangka menengah, yaitu yang mencakup waktu antara 3 sampai 18 bulan. Misalnya, peramalan untuk perencanaan penjualan, perencanaan produksi, dan perencanaan tenaga kerja tidak tetap. 3. Peramalan jangka pendek, yaitu untuk jangka waktu kurang dari 3 bulan. Misalnya, peramalan dalam hubungannya dengan perencanaan pembelian material, penjadwalan kerja, dan penugasan karyawan. ardiprawiro. staff. gunadarma. ac. id

METODE SERIAL WAKTU (TIME SERIES) v Metode serial waktu (time series) adalah metode yang digunakan untuk menganalisis serangkaian data yang merupakan fungsi dari waktu. v Tujuan analisisnya ialah untuk menemukan pola deret variabel yang bersangkutan berdasarkan atas nilai variabel pada masa sebelumnya, dan mengekstrapolasikan pola itu untuk membuat peramalan nilai variabel itu pada masa datang. v Pengolahan data kuantitatif dari serial waktu dapat dilakukan dengan beberapa metode dasar, sebagai berikut: a) Rata-rata bergerak, b) Pemulusan eksponensial, dan c) Dekomposisi. ardiprawiro. staff. gunadarma. ac. id

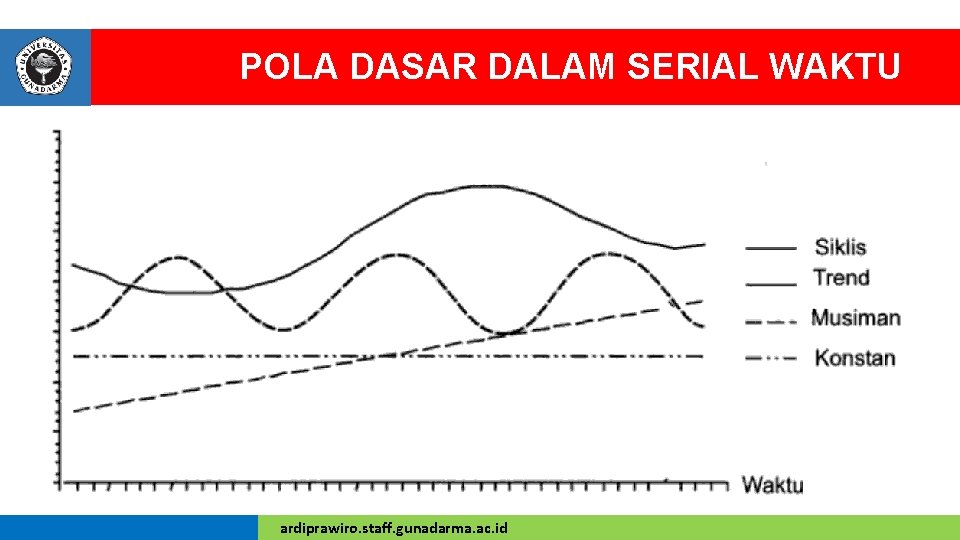
POLA DASAR DALAM SERIAL WAKTU ardiprawiro. staff. gunadarma. ac. id

POLA DASAR DALAM SERIAL WAKTU v Pola dari serangkaian data dalam serial waktu dapat dikelompokkan ke dalam pola dasar sebagai berikut: 1. Horizontal (konstan), yaitu apabila data berfluktuasi di sekitar rata-rata secara stabil. 2. Kecenderungan (trend), yaitu apabila data mempunyai kecenderungan, baik yang arahnya meningkat atau menurun dari waktu ke waktu. 3. Musiman (seasonal), yaitu apabila polanya merupakan gerakan yang berulang -ulang secara teratur dalam setiap periode tertentu, misalnya tahunan, triwulanan, bulanan atau mingguan. 4. Siklus (cyclical), yaitu apabila data dipengaruhi oleh fluktuasi ekonomi jangka panjang, seperti daur hidup bisnis. 5. Residu atau variasi acak, yaitu apabila data tidak teratur sama sekali. Data yang bersifat residu tidak dapat digambarkan. ardiprawiro. staff. gunadarma. ac. id

METODE RATA-RATA BERGERAK SEDERHANA • ardiprawiro. staff. gunadarma. ac. id

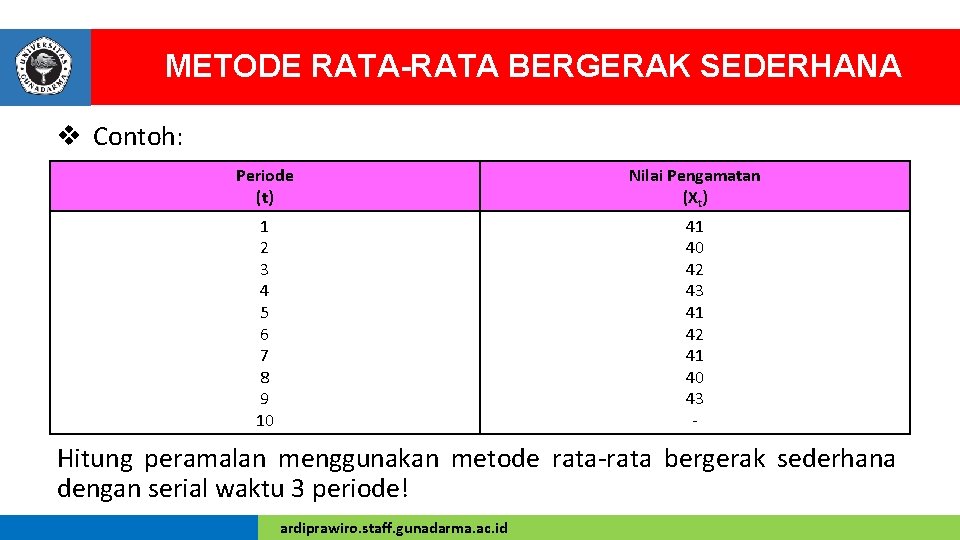
METODE RATA-RATA BERGERAK SEDERHANA v Contoh: Periode (t) Nilai Pengamatan (Xt) 1 2 3 4 5 6 7 8 9 10 41 40 42 43 41 42 41 40 43 - Hitung peramalan menggunakan metode rata-rata bergerak sederhana dengan serial waktu 3 periode! ardiprawiro. staff. gunadarma. ac. id

METODE RATA-RATA BERGERAK SEDERHANA v Prakiraan permintaan pada periode ke-4 dapat dihitung sebagai berikut (karena serial waktu adalah 3 periode maka perhitungan dimulai dari periode 4): F 4 = (Xt 1 + Xt 2 + Xt 3) / N = (41 + 40 + 42) / 3 = 41 v Prakiraan permintaan pada periode ke-5 dapat dihitung sebagai berikut: F 5 = (Xt 2 + Xt 3 + Xt 4) / N = (40 + 42 + 43) / 3 = 41, 7 v Prakiraan permintaan pada periode ke-5 dapat dihitung sebagai berikut: F 6 = (Xt 3 + Xt 4 + Xt 5) / N = (42 + 43 + 41) / 3 = 42 dan seterusnya. . ardiprawiro. staff. gunadarma. ac. id

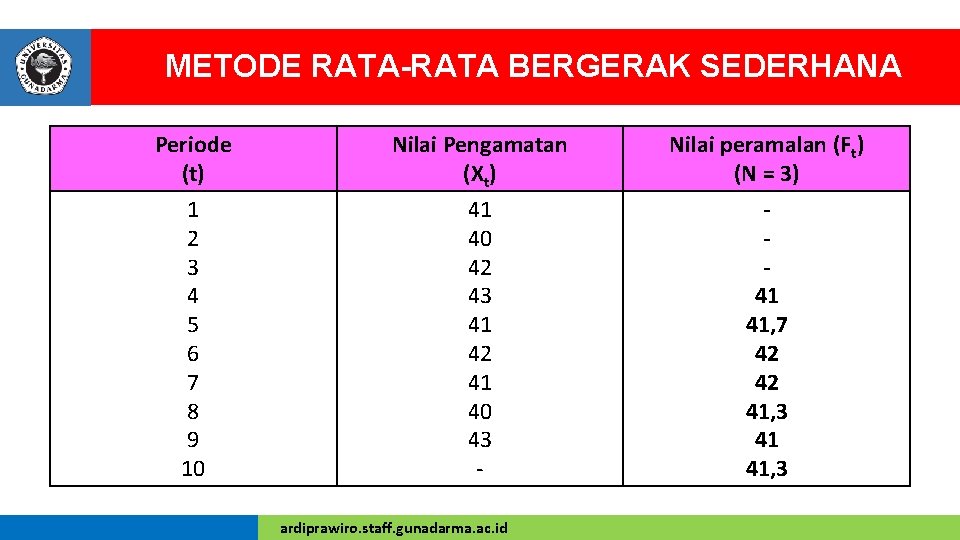
METODE RATA-RATA BERGERAK SEDERHANA Periode (t) Nilai Pengamatan (Xt) Nilai peramalan (Ft) (N = 3) 1 2 3 4 5 6 7 8 9 10 41 40 42 43 41 42 41 40 43 - 41 41, 7 42 42 41, 3 41 41, 3 ardiprawiro. staff. gunadarma. ac. id

METODE RATA-RATA BERGERAK TERTIMBANG • ardiprawiro. staff. gunadarma. ac. id

METODE RATA-RATA BERGERAK TERTIMBANG v Contoh: Periode (t) Nilai Pengamatan (Xt) 1 2 3 4 5 6 7 8 9 10 41 40 42 43 41 42 41 40 43 - Hitung peramalan menggunakan metode rata-rata bergerak tertimbang dengan serial waktu 3 periode! ardiprawiro. staff. gunadarma. ac. id

METODE RATA-RATA BERGERAK TERTIMBANG v Prakiraan permintaan pada periode ke-4 dapat dihitung sebagai berikut (karena serial waktu adalah 3 periode maka perhitungan dimulai dari periode 4): F 4 = (W 1 x. Xt 1 + W 2 x. Xt 2 + W 3 x. Xt 3) / W 1 + W 2 + W 3 F 4 = (1 x 41 + 2 x 40 + 3 x 42) / 1 + 2 + 3 = 41, 7 v Prakiraan permintaan pada periode ke-5 dapat dihitung sebagai berikut: F 4 = (W 2 x. Xt 2 + W 3 x. Xt 3 + W 4 x. Xt 4) / W 2 + W 3 + W 4 F 5 = (2 x 40 + 3 x 42 + 4 x 43) / 2 + 3 + 4 = 34, 4 dan seterusnya. . ardiprawiro. staff. gunadarma. ac. id

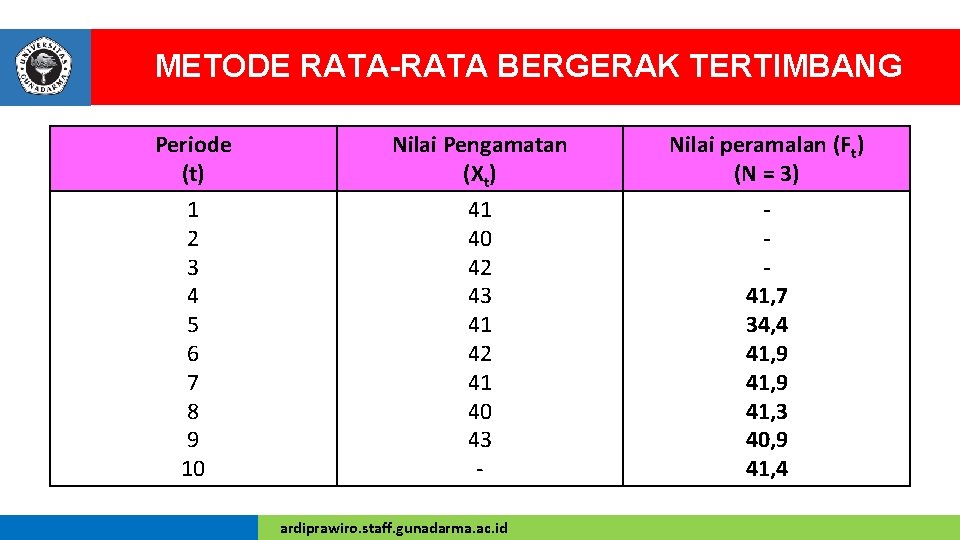
METODE RATA-RATA BERGERAK TERTIMBANG Periode (t) Nilai Pengamatan (Xt) Nilai peramalan (Ft) (N = 3) 1 2 3 4 5 6 7 8 9 10 41 40 42 43 41 42 41 40 43 - 41, 7 34, 4 41, 9 41, 3 40, 9 41, 4 ardiprawiro. staff. gunadarma. ac. id

METODE PEMULUSAN EKSPONENSIAL TUNGGAL v Metode pemulusan eksponensial tunggal (single exponential smoothing) menambahkan parameter α dalam model untuk mengurangi faktor kerandoman. Metode ini digunakan untuk serial data yang memiliki pola horizontal. v Nilai peramalan dapat dicari dengan menggunakan rumus berikut: Ft+1= α x Xt + (1 – α) x Ft v Di mana: Xt = data permintaan pada periode t α = faktor/konstanta pemulusan Ft+1 = peramalan untuk periode t ardiprawiro. staff. gunadarma. ac. id

METODE PEMULUSAN EKSPONENSIAL TUNGGAL v Contoh: Periode (t) Nilai Pengamatan (Xt) 1 2 3 4 5 6 7 8 9 10 41 40 42 43 41 42 41 40 43 - Hitung peramalan menggunakan metode pemulusan eksponensial tunggal dengan konstanta pemulusan (α) sebesar 0, 1! ardiprawiro. staff. gunadarma. ac. id

METODE PEMULUSAN EKSPONENSIAL TUNGGAL v Prakiraan permintaan pada periode ke-2 dapat dihitung sebagai berikut (nilai F 1 selalu sama dengan X 1): F 2 = α x X 1 + (1 – α) x F 1 = 0, 1 x 41 + (1 – 0, 1) x 41 = 41 v Prakiraan permintaan pada periode ke-3 dapat dihitung sebagai berikut: F 3 = α x X 2 + (1 – α) x F 2 = 0, 1 x 40 + (1 – 0, 1) x 41 = 40, 9 v Prakiraan permintaan pada periode ke-4 dapat dihitung sebagai berikut: F 4 = α x X 3 + (1 – α) x F 3 = 0, 1 x 42 + (1 – 0, 1) x 40, 9 = 41 dan seterusnya. . ardiprawiro. staff. gunadarma. ac. id

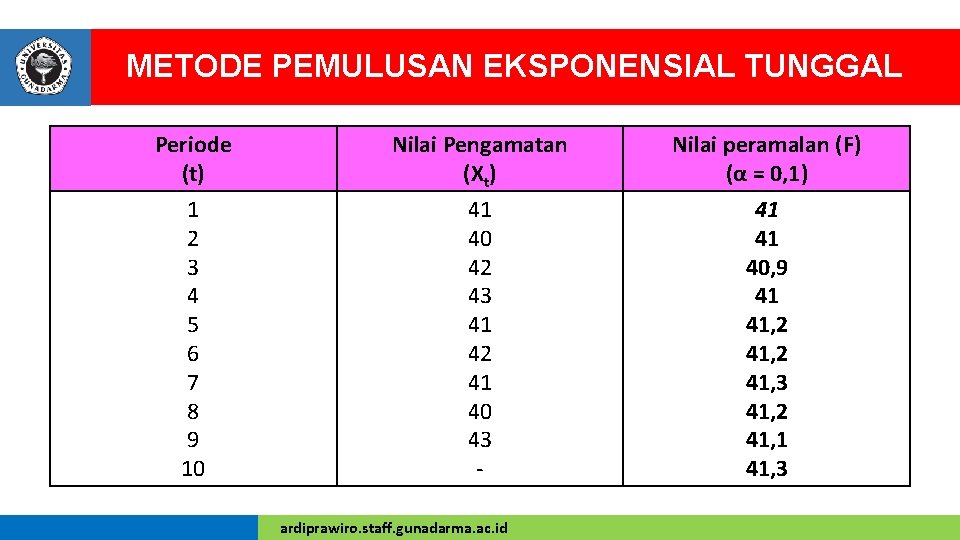
METODE PEMULUSAN EKSPONENSIAL TUNGGAL Periode (t) Nilai Pengamatan (Xt) Nilai peramalan (F) (α = 0, 1) 1 2 3 4 5 6 7 8 9 10 41 40 42 43 41 42 41 40 43 - 41 41 40, 9 41 41, 2 41, 3 41, 2 41, 1 41, 3 ardiprawiro. staff. gunadarma. ac. id

METODE PEMULUSAN EKSPONENSIAL LINEAR v Metode pemulusan eksponensial linear digunakan untuk melakukan peramalan serial data yang memiliki unsur kecenderungan (trend). v Salah satu metode pemulusan eksponensial linear, yang diperkenalkan oleh Holt, menggunakan persamaan sebagai berikut: Pemulusan standar → St = α x Xt + (1 – α) x (Ft-1 + Tt-1) Pemulusan tren → Tt = β x (St – St-1) + (1 – β) x Tt-1 Peramalan → Ft+m = St +Tt x m ardiprawiro. staff. gunadarma. ac. id

METODE PEMULUSAN EKSPONENSIAL LINEAR • ardiprawiro. staff. gunadarma. ac. id

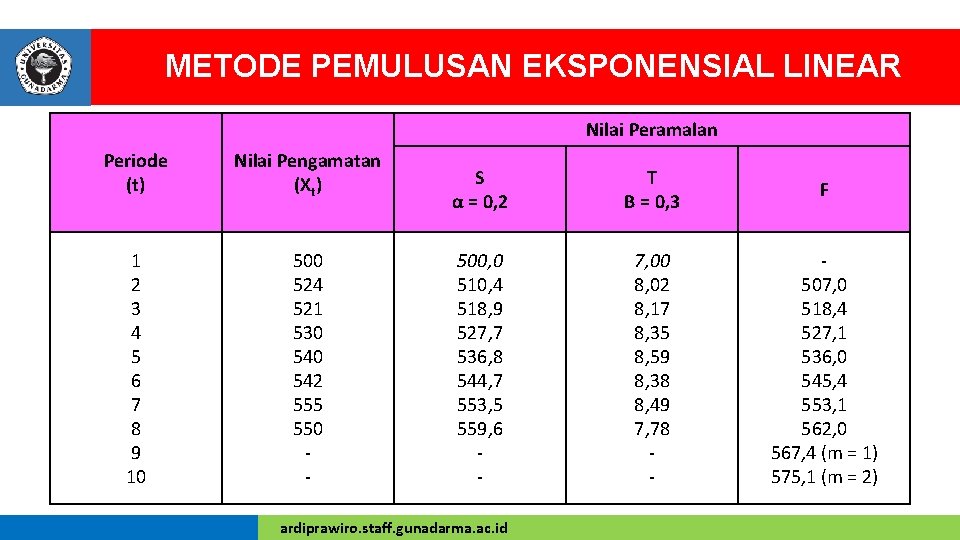
METODE PEMULUSAN EKSPONENSIAL LINEAR Nilai Peramalan Periode (t) Nilai Pengamatan (Xt) 1 2 3 4 5 6 7 8 9 10 500 524 521 530 542 555 550 - S α = 0, 2 T Β = 0, 3 F 500, 0 510, 4 518, 9 527, 7 536, 8 544, 7 553, 5 559, 6 - 7, 00 8, 02 8, 17 8, 35 8, 59 8, 38 8, 49 7, 78 - 507, 0 518, 4 527, 1 536, 0 545, 4 553, 1 562, 0 567, 4 (m = 1) 575, 1 (m = 2) ardiprawiro. staff. gunadarma. ac. id

METODE PEMULUSAN EKSPONENSIAL MUSIMAN • ardiprawiro. staff. gunadarma. ac. id

METODE PEMULUSAN EKSPONENSIAL MUSIMAN • ardiprawiro. staff. gunadarma. ac. id

KETERBATASAN METODE EKSPONENSIAL v Permasalahan umum yang dihadapi apabila menggunakan model pemulusan eksponensial adalah memilih konstanta pemulusan yang diperkirakan tepat. Adapun panduan untuk memperkirakan nilai α yaitu antara lain: 1. Apabila pola historis dari data aktual permintaan sangat bergejolak atau tidak stabil dari waktu ke waktu, kita memilih nilai a mendekati 1. Biasanya di pilih nilai α = 0. 9; namun pembaca dapat mencoba nilai α yang lain yang mendekati 1 seperti 0, 8; 0, 99 tergantung sejauh mana gejolak dari data itu. 2. Apabila pola historis dari data aktual permintaan tidak berfluktuasi atau relatif stabil dari waktu ke waktu maka kita memilih nilai a yang mendekati nol, katakanlah α = 0. 2; 0. 05; 0. 01 tergantung sejauh mana kestabilan data itu, semakin stabil nilai a yang dipilih harus semakin kecil menuju ke nilai nol. ardiprawiro. staff. gunadarma. ac. id

KEKUATAN METODE EKSPONENSIAL v Kelebihan utama dari metode pemulusan eksponensial adalah dilihat dari kemudahan dalam operasi yang relatif rendah, ada sedikit keraguan apakah ketepatan yang lebih baik selalu dapat dicapai dengan menggunakan sistem kuantitatif ataukah metode dekomposisi yang secara intuitif menarik, namun dalam hal ini jika diperlukan peramalan untuk ratusan item. ardiprawiro. staff. gunadarma. ac. id

REFERENSI v Herjanto, Eddy. 2015. Manajemen Operasi, Edisi 3, Jakarta: Grasindo. ardiprawiro. staff. gunadarma. ac. id

TERIMA KASIH