TEKNIK PROYEKSI BISNIS BAB 8 ANALISIS METODE BOX

TEKNIK PROYEKSI BISNIS BAB 8 ANALISIS METODE BOX JENKINS Ardiprawiro S. E. , MMSI

TUJUAN PEMBELAJARAN Setelah mempelajari bab ini, Anda diharapkan dapat: “Mampu menjelaskan notasi, teknik, asumsi serta penerapan metode Box Jenkins” ardiprawiro. staff. gunadarma. ac. id

METODE BOX JENKINS v Metode Box Jenkins adalah satu teknik peramalan model time series yang hanya berdasarkan perilaku masa lalu variabel yang diramal. v Metode Box Jenkins terdiri atas beberapa teknik yaitu: 1. Model Autoregresif (Autoregressive/AR) 2. Model Rata-rata Bergerak (Moving Average/MA) 3. Model Autoregresif Rata-rata Bergerak (ARMA) 4. Model Autoregresif Integrasi Rata-rata Bergerak (ARIMA) ardiprawiro. staff. gunadarma. ac. id

NOTASI METODE BOX JENKINS v Notasi metode Box Jenkins adalah: ARIMA (p, d, q) di mana: p = derajat autoregresif (AR) d = derajat perbedaan (differential/d) q = derajat rata-rata bergerak (MA) ardiprawiro. staff. gunadarma. ac. id

MODEL AUTOREGRESIF v Model autoregresif (AR) menunjukkan Yt sebagai fungsi linier dari sejumlah Yt aktual sebelumnya, atau dinyatakan dalam rumus: Yt = b 0 + b 1 Yt-1 + b 2 Yt-2 +. . . + bp. Yt-pet di mana: Yt = variabel dependen Yt-1, Yt-2, Yt-p = variabel bebas b 0, b 1, bp = koefisien regresi; lag dari variabel terikat e = residual p = tingkat AR atau derajat autoregresif ardiprawiro. staff. gunadarma. ac. id

MODEL AUTOREGRESIF v Ada beberapa klasifikasi model AR: 1. Model random (white noise series), yaitu model di mana suatu data deret waktu Yt, mengandung unsur rata-rata hitung (μ) dan unsur kesalahan random (et), yang bebas dari masalah autokorelasi. Notasi Box Jenkins ARIMA (0, 0, 0). Ini dirumuskan menjadi: Yt = μ + et 2. Model autoregresif tingkat p, artinya model mengandung autokorelasi antara Yt dan Yt-p. Yt = μ + Yt-1 + et, notasi Box Jenkins ARIMA (1, 0, 0) atau Yt – Yt-1 = μ + et, notasi Box Jenkins ARIMA (1, 1, 0). ardiprawiro. staff. gunadarma. ac. id

MODEL RATA-RATA BERGERAK v Model rata-rata bergerak (MA), meramalkan nilai Yt berdasarkan kombinasi kesalahan linier masa lampau (lag), atau: Yt = w 0 + w 1 et-1 – w 2 et-2 -. . . – wqet-q + et di mana: Yt = variabel dependen et-1, et-2, et-q = variabel bebas; lag dari residual w 0, w 1, wq = bobot et = residual q = tingkat MA atau derajat rata-rata bergerak ardiprawiro. staff. gunadarma. ac. id

MODEL RATA-RATA BERGERAK v Nilai “q” dalam rata-rata bergerak (MA) menunjukkan model MA. Model MA (1) atau notasi Box Jenkins ARIMA (0, 1) adalah: Yt = w 0 + et - w 1 et-1 v Model MA (2) atau notasi Box Jenkins ARIMA (0, 0, 2) adalah: Yt = w 0 + et – w 1 et-1 + w 2 et-2 ardiprawiro. staff. gunadarma. ac. id

MODEL AUTOREGRESIF RATA-RATA BERGERAK v Perilaku suatu data deret waktu selain dapat dijelaskan dengan baik melalui model AR, model MA, dapat juga dijelaskan dengan penggabungan antara model AR dan model MA yang disebut Autoregressive-Moving Average (ARMA). v Model AR, MA, ARMA mensyaratkan bahwa data deret waktu yang diamati mempunyai sifat stasioner. v Data deret waktu (time series) dikatakan stasioner jika memenuhi tiga kriteria yaitu: 1. Jika data deret waktu mempunyai rata-rata, 2. Jika data deret waktu mempunyai varian, dan 3. Jika data deret waktu mempunyai kovarian yang konstan. v Data deret waktu yang tidak memenuhi kriteria di atas kemungkinan menjadi stasioner melalui proses diferensial. ardiprawiro. staff. gunadarma. ac. id

MODEL AUTOREGRESIF INTEGRASI RATA-RATA BERGERAK v Model dengan data yang stasioner melalui proses diferensial disebut dengan model autoregressive integrated moving average (ARIMA). v Model ARIMA dapat ditulis dengan persamaan: Yt = b 0 + b 1 Yt-1 + b 2 Yt-2 +. . . + bp. Yt-p – w 1 et-1 – w 2 et-2 -. . . – wqet-q + et v Notasi model ARIMA ditentukan oleh jumlah periode variabel independen baik dari nilai sebelumnya dari variabel dependen maupun nilai residualnya. Yt = b 0 + b 1 Yt-1 – w 1 et-1 + et → ARIMA (1, 0, 1) Yt = b 0 + b 1 Yt-1 + b 2 Yt-2 – w 1 et-1 + et → ARIMA (2, 0, 1) Yt = b 0 + b 1 Yt-1 – w 1 et-1 – w 2 et-2 + et → ARIMA (1, 0, 2) ardiprawiro. staff. gunadarma. ac. id

ASUMSI METODE BOX JENKINS v Metode Box Jenkins memiliki beberapa asumsi, antara lain: a) Data deret waktu yang akan dianalisis dan diramalkan bersifat stasioner. Secara intuitif, data dikatakan stasioner jika data tersebut berfluktuasi secara random di sekitar nilai rata-ratanya. b) Nilai rata-rata dari variabel yang diteliti berfluktuasi di sekitar nilai nol yang tetap. ardiprawiro. staff. gunadarma. ac. id

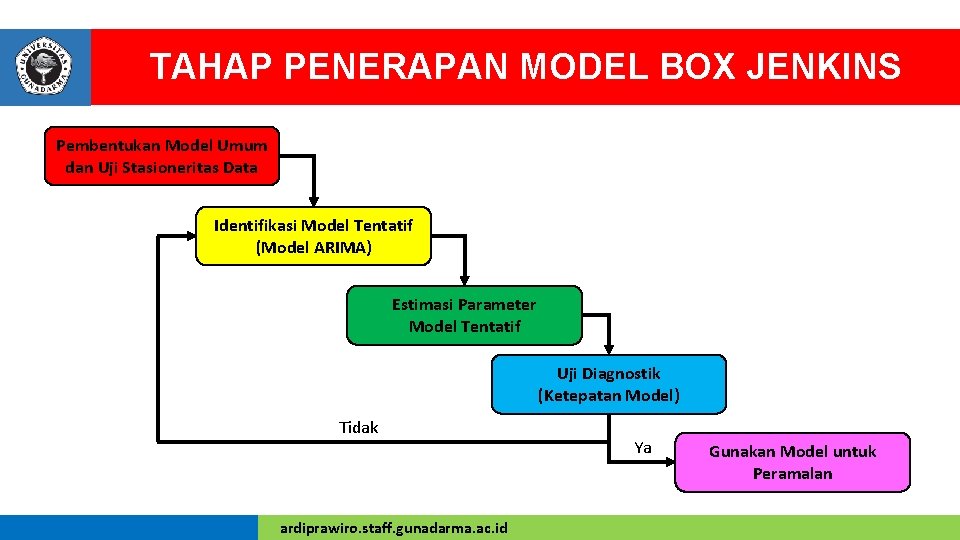
TAHAP PENERAPAN MODEL BOX JENKINS Pembentukan Model Umum dan Uji Stasioneritas Data Identifikasi Model Tentatif (Model ARIMA) Estimasi Parameter Model Tentatif Uji Diagnostik (Ketepatan Model) Tidak ardiprawiro. staff. gunadarma. ac. id Ya Gunakan Model untuk Peramalan

TAHAP IDENTIFIKASI v Pada tahap identifikasi model tentatif, terdapat beberapa langkah yang dilakukan: 1. Menentukan apakah sebuah data deret waktu bersifat stasioner (nilai rata-rata tidak bergeser sepanjang waktu). Apabila data tidak bersifat stasioner, maka konversi data harus dilakukan (agar menjadi stasioner) dengan menggunakan proses diferensial. 2. Menentukan model yang akan digunakan. Penentuan model dilakukan dengan cara membandingkan koefisien autokorelasi (ACF) dan autokorelasi parsial (PACF) dari data dengan model ARIMA untuk menentukan model yang paling sesuai. ardiprawiro. staff. gunadarma. ac. id

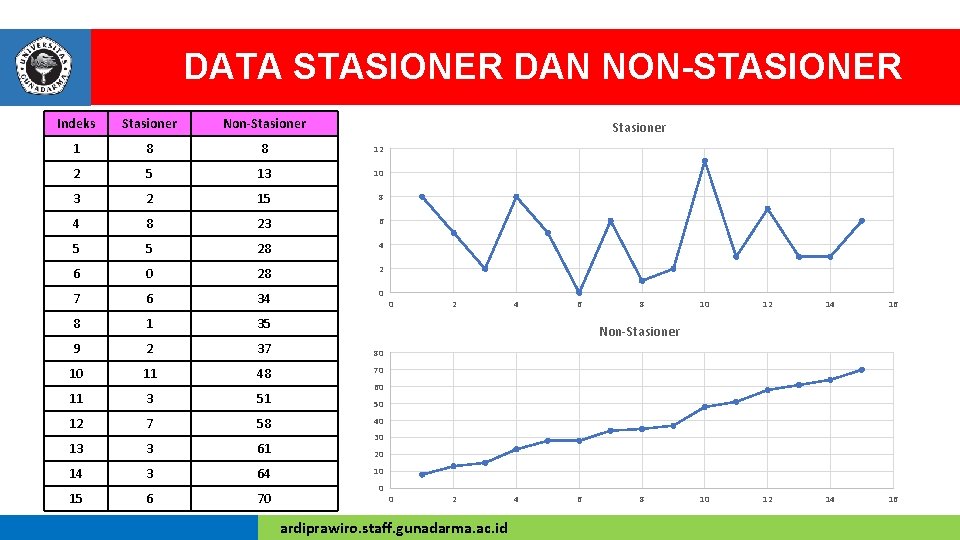
DATA STASIONER DAN NON-STASIONER Indeks Stasioner Non-Stasioner 1 8 8 12 2 5 13 10 3 2 15 8 4 8 23 6 5 5 28 4 6 0 28 2 7 6 34 0 8 1 35 9 2 37 80 10 11 48 70 11 3 51 12 7 58 13 3 61 14 3 64 15 6 70 Stasioner 0 2 4 6 8 10 12 14 16 Non-Stasioner 60 50 40 30 20 10 0 0 2 ardiprawiro. staff. gunadarma. ac. id 4 6 8

PROSES DIFERENSIAL v Proses diferensial digunakan untuk melakukan konversi data yang tidak stasioner menjadi data yang stasioner (syarat untuk implementasi ARIMA). v Diferensial notasi 1, didefinisikan sebagai: X’ = Xt – Xt-1 v Diferensial notasi 2, didefinisikan sebagai: X’’ = X’t – X’t-1, atau X’’ = (Xt – Xt-1) – (Xt-1 – Xt-2) ardiprawiro. staff. gunadarma. ac. id

PROSES DIFERENSIAL v Ambil contoh kita ingin menytasionerkan data dari tabel nonstasioner, maka (dikarenakan indeks 1 tidak ada data awal maka dia tidak dapat distasioner): X’ 2 = X 2 – X 2 -1 = 13 – 8 = 5 X’ 3 = X 3 – X 3 -1 = 15 – 13 = 2 X’ 4 = X 4 – X 4 -1 = 23 – 15 = 8 X’ 5 = X 5 – X 5 -1 = 28 – 23 = 5 X’ 6 = X 6 – X 6 -1 = 28 – 28 = 0 dan seterusnya. ardiprawiro. staff. gunadarma. ac. id

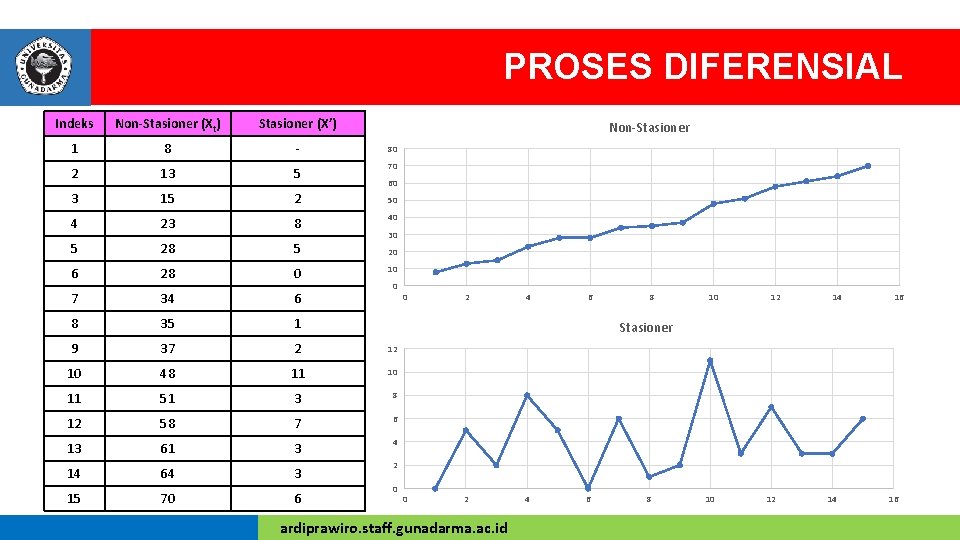
PROSES DIFERENSIAL Indeks Non-Stasioner (Xt) Stasioner (X’) 1 8 - 2 13 5 3 15 2 4 23 8 5 28 5 6 28 0 7 34 6 8 35 1 9 37 2 12 10 48 11 10 11 51 3 8 12 58 7 6 13 61 3 4 14 64 3 15 70 6 Non-Stasioner 80 70 60 50 40 30 20 10 0 0 2 4 6 8 10 12 14 16 Stasioner 2 0 0 2 ardiprawiro. staff. gunadarma. ac. id 4 6 8 10 12 14 16

DASAR-DASAR ANALISIS BOX JENKINS • ardiprawiro. staff. gunadarma. ac. id

DASAR-DASAR ANALISIS BOX JENKINS 2. Koefisien Autokorelasi Parsial (Parsial Autocorrelation Factor/PACF), yaitu korelasi antara Xt dengan Xt+k, dengan mengabaikan ketidakbebasan Xt+1, Xt+2, . . . , Xt+k-1, sehingga Xt dianggap sebagai konstanta, Xt = xt, t = t+1, t+2, . . . , t+k-1. ρ(kk) = kor(Xt. Xt+k. IXt+1 = xt+1, Xt+2 = xt+2, . . . , Xt+k-1 = xt+k-1) ardiprawiro. staff. gunadarma. ac. id

TAHAP ESTIMASI • ardiprawiro. staff. gunadarma. ac. id

TAHAP DIAGNOSTIK • ardiprawiro. staff. gunadarma. ac. id

TAHAP PERAMALAN v Pada tahap peramalan dengan model, terdapat beberapa langkah yang dilakukan: 1. Setelah model yang layak telah ditentukan maka selanjutnya peramalan untuk satu atau beberapa periode ke depan dapat dilakukan dengan menggunakan metode ARIMA yang telah dipilih. 2. Apabila pola dari deret waktu berubah, data yang baru dapat digunakan untuk melakukan estimasi ulang terhadap metode ARIMA atau membangun metode ARIMA yang baru. ardiprawiro. staff. gunadarma. ac. id

REFERENSI v Wardhono, Adhitya dkk. , 2019. Analisis Data Time Series dalam Model Makroekonomi. Jember: Pustaka Abadi. v Makridakis, S. C. Wheelwright, dan V. E. Mc. Gree. , 1983. Forecasting: Methods and Applications. New York: John Wiley and Sons. v Pindyck, R, S. Dan D. L. Rubinfeld, 1994. Econometric Models and Economic Forecasts. Singapur: Mc. Graw-Hill ardiprawiro. staff. gunadarma. ac. id

TERIMA KASIH