LOG 770 Systmes Intelligents Charg de cours Yazid

LOG 770 Systèmes Intelligents Chargé de cours : Yazid Attabi Local: CRIM Téléphone: (514) 840 1235 #2299 Courriel: yazid. attabi@crim. ca Responsable de cours : Pierre Dumouchel, ing. , Ph. D. , Local: A-3498 Téléphone: (514) 396 8996 Courriel: Pierre. Dumouchel@etsmtl. ca Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

CH PITRE 4: Méthodes paramétriques Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Résumé n Au chapitre 3, nous avons vu comment prendre une décision optimale à l’aide d’un modèle probabilistes. n Dans ce chapitre, nous voyons comment estimer ces probabilités d’une façon paramétrique pour le cas de paramètre à une dimension. n Dans le prochain chapitre, nous étudierons le problème de variable à plusieurs dimensions n Nous verrons dans d’autres chapitres comment faire une modélisation semiparamétrique ou non-paramétrique. 3 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Règle de Bayes apriori vraisemblance aposteriori évidence n Comment modéliser l’aposteriori; ¨ l’évidence; ¨ la vraisemblance; ¨ l’apriori? ¨ 4 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Méthode paramétrique n n n Assume que les données sont représentées par une distribution de probabilité ou par des fréquences relatives d’apparition. Assume que les échantillons de données sont indépendants et identiquement distribués. Avantage: Nécessite peu de paramètres de modélisation: moyenne et variance. Nous dénoterons ces paramètres par θ. ¨ Estime ces paramètres à partir d’échantillons de données ¨ 5 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Estimation paramétrique n n n Soit des données X = { xt }t qui suivent une distribution quelconque xt ~ p (x) Estimation paramétrique (moyenne et variance): Assumons une forme p (x | θ) et un estimé θ et des statistiques suffisantes, en utilisant X e. g. , N ( μ, σ2) où θ = { μ, σ2} En d’autres mots, nous voulons trouver θ qui correspond le plus fidèlement à la distribution des données. 6 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Estimation de la vraisemblance maximale n Vraisemblance de θ étant donné l’échantillon X l (θ|X) : p (X |θ) = ∏t p (xt|θ) n Vraisemblance logarithmique L(θ|X) : log l (θ|X) = ∑t log p (xt|θ) n Estimateur de la vraisemblance maximale (MLE) θ* = argmaxθ L(θ|X) 7 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Exemples: Bernoulli/Multinomial n Bernoulli: Deux états, échec/succès, x dans {0, 1} P (x) = pox (1 – po ) (1 – x) L (po|X) = log ∏t poxt (1 – po ) (1 – xt) MLE: po = ∑t xt / N n Multinomial: K>2 états, xi dans {0, 1} P (x 1, x 2, . . . , x. K) = ∏i pixi L(p 1, p 2, . . . , p. K|X) = log ∏t ∏i pixit MLE: pi = ∑t xit / N 8 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

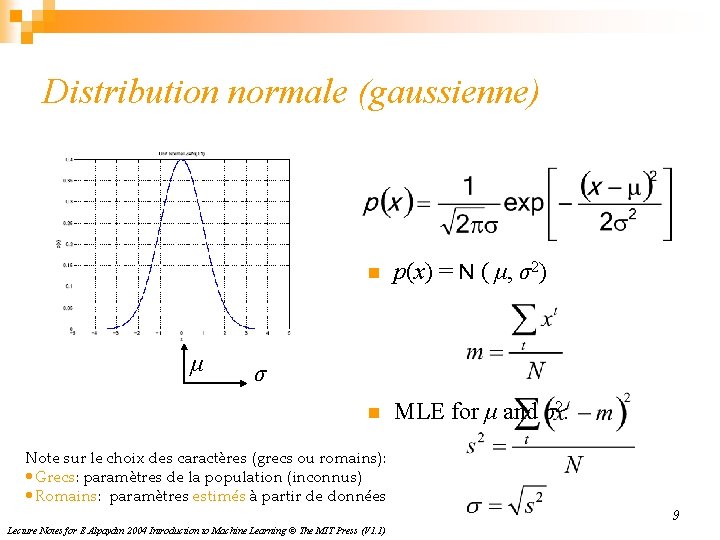
Distribution normale (gaussienne) μ n p(x) = N ( μ, σ2) n MLE for μ and σ2: σ Note sur le choix des caractères (grecs ou romains): • Grecs: paramètres de la population (inconnus) • Romains: paramètres estimés à partir de données Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1) 9

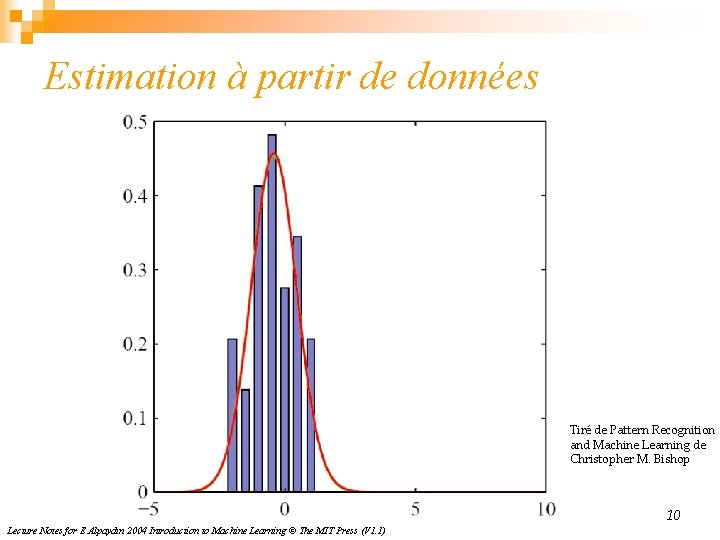
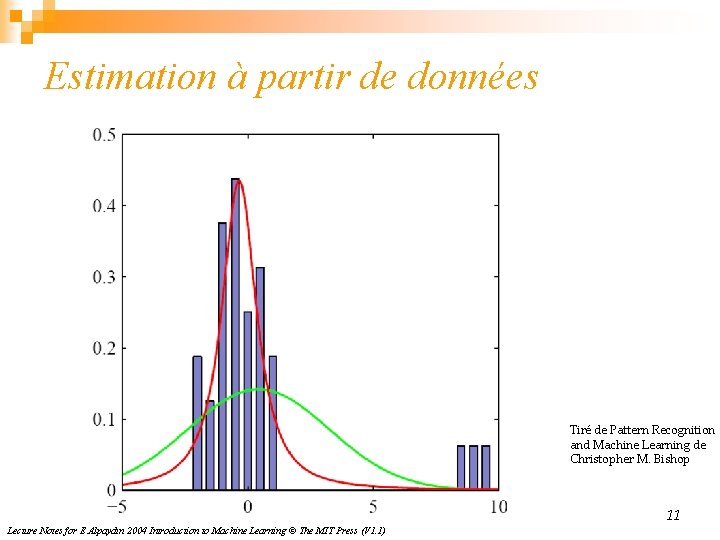
Estimation à partir de données Tiré de Pattern Recognition and Machine Learning de Christopher M. Bishop 10 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

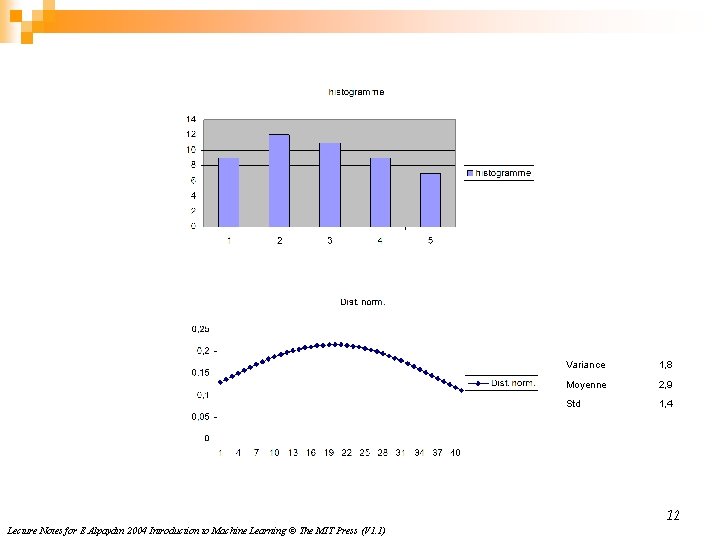
Estimation à partir de données Tiré de Pattern Recognition and Machine Learning de Christopher M. Bishop 11 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Variance 1, 8 Moyenne 2, 9 Std 1, 4 12 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Biais et Variance n Quelle est la qualité de l’estimation paramétrique? ¨ Le vrai paramètre θ est inconnu de même que sa distribution. ¨ Estimateur di = d (Xi) pour les échantillons Xi ¨ Biais: bθ(d) = E [d] – θ n ¨ bθ(d) = 0 si l’estimateur est parfait. Variance: E [(d–E [d])²] 13 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Biais et Variance n Évaluation de la qualité de l’estimation paramétrique selon le critère de l’erreur quadratique moyenne: r (d, θ) = E [(d–θ)²] =… = (E [d] – θ)² + E [(d–E [d])²] = Biais² + Variance 14 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Estimateur bayesien n Exemple: un expert nous avise que les données suivent: Une distribution normale; ¨ Que la moyenne de ces données est d’environ 7; ¨ Que 90% des données sont entre 5 et 9; ¨ n Si 90% alors les données sont entre ± 1, 64σ de la moyenne n Pr{ -1, 64 σ < (θ – μ) < 1, 64 σ } = 0, 9 n Mais 1, 64* σ = 2 n Alors p(θ) = N ( μ, σ2) = N ( 7 , (2/1, 64)2 ) σ = 2/1, 64 15 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Estimateur bayesien n n Traiter θ comme une var. aléatoire avec apriori p (θ) Règle de Bayes: p (θ|X) = p(X|θ) p(θ) / p(X) n Plein: p(x|X) = ∫ p(x|θ) p(θ|X) dθ Maximum a Posteriori (MAP): θMAP = argmaxθ p(θ|X) Maximum Likelihood (ML): θML = argmaxθ p(X|θ) n Bayes: θBayes’ = E[θ|X] = ∫ θ p(θ|X) dθ n n 16 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Estimateur bayesien: Exemple n xt ~ N (θ, σo 2) and θ ~ N ( μ, σ2) θML = m θMAP = θBayes’ = n Note: MAP et Bayes n n Assument des distributions unimodales; ¨ Sont équivalents si N est grand. ¨ 17 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Classification paramétrique 18 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Classification paramétrique 19 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

n Étant donné l’éch. n Estimation ML n Discriminant devient 20 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

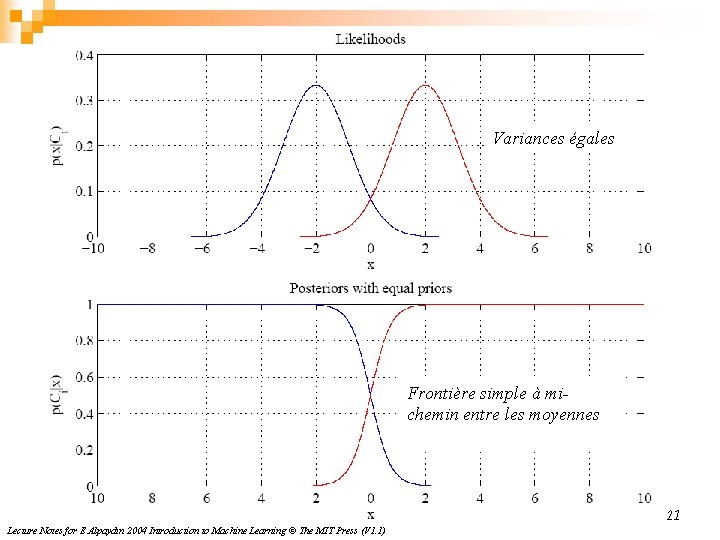
Variances égales Frontière simple à michemin entre les moyennes 21 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

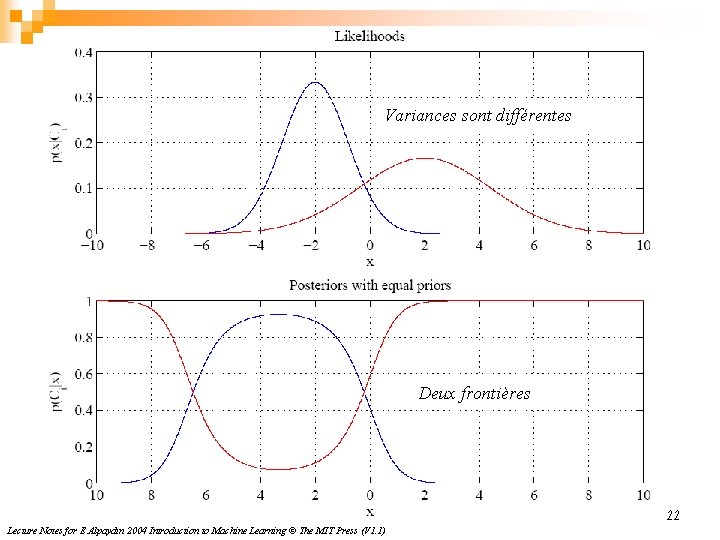
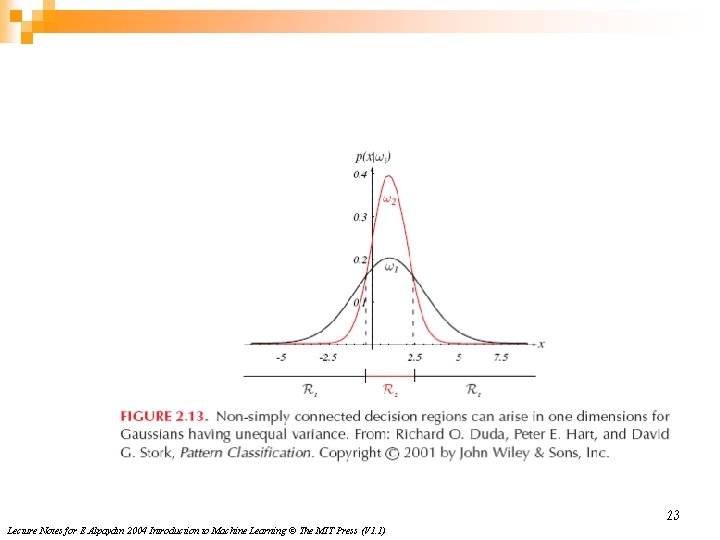
Variances sont différentes Deux frontières 22 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

23 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Régression n Avec la régression, nous voulons estimer un nombre et non pas une probabilité. La sortie, r, est appelée la variable dépendante; Les entrées, x, sont appelés les variables indépendantes ¨ n Sortie: fonction(x )+ bruit ε f(x) est inconnu. Nous allons l’estimer par g(x |⊖) 24 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Régression 25 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Régression: du Log. L jusqu’à l’Erreur n Le second terme peut être éliminé car il ne dépend pas de notre estimateur ⊖. Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1) 26

Régression: du Log. L jusqu’à l’Erreur n n 1 er terme de la seconde équation ne dépend pas de ⊖, il n’est donc pas considéré; σ de la seconde équation ne dépend pas de ⊖, il n’est donc pas considéré; Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1) 27

Régression: de Log. L à l’Erreur Estimation du minimum au carré (Least Squares Estimate) Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1) 28

Régression linéaire n Supposons une régression linéaire: n Insérons dans et trouvons le minimum par rapport à w 0 et w 1 29 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Régression linéaire 30 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Régression polynomiale 31 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

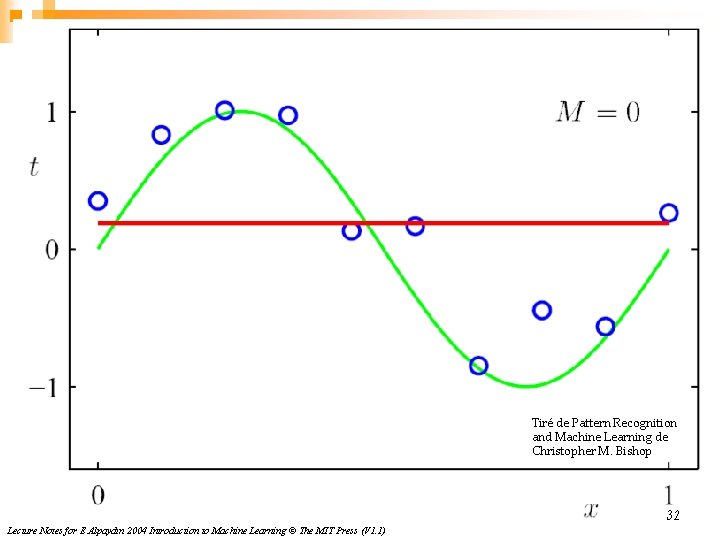
Tiré de Pattern Recognition and Machine Learning de Christopher M. Bishop 32 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

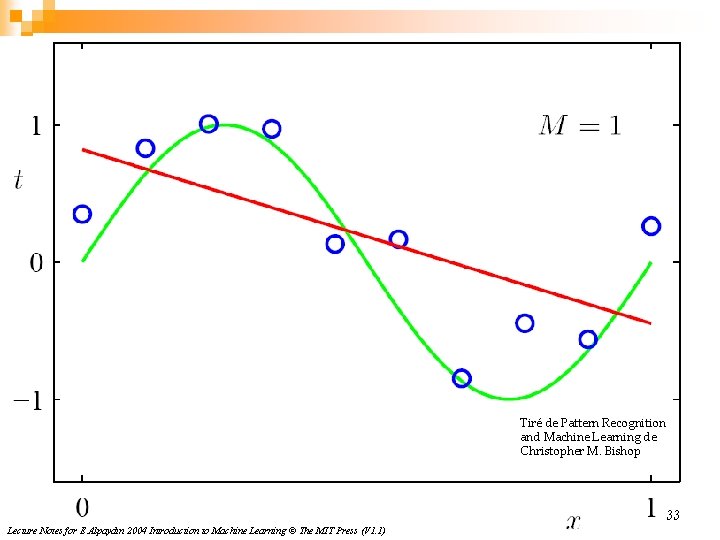
Tiré de Pattern Recognition and Machine Learning de Christopher M. Bishop 33 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

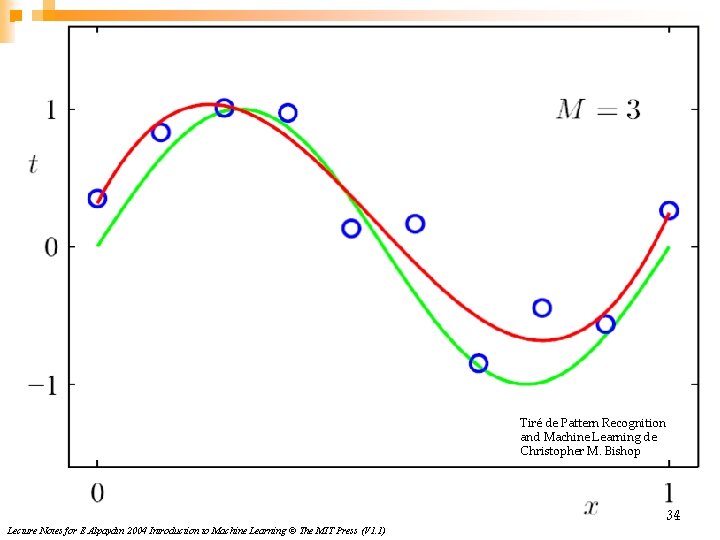
Tiré de Pattern Recognition and Machine Learning de Christopher M. Bishop 34 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

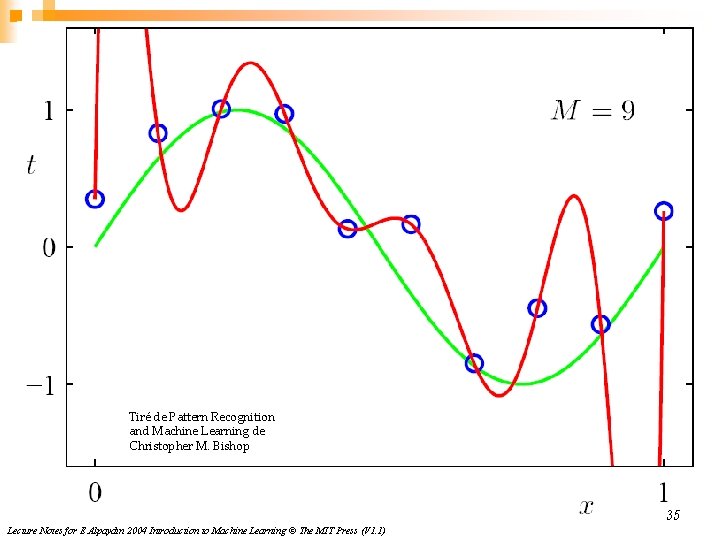
Tiré de Pattern Recognition and Machine Learning de Christopher M. Bishop 35 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Autres mesures d’erreur n Erreur quadratique: n Erreur relative quadratique: n Erreur absolue: E (θ|X) = ∑t |rt – g(xt|θ)| n Erreur ε-sensitive : E (θ|X) = ∑ t 1(|rt – g(xt|θ)|>ε) (|rt – g(xt|θ)| – ε) 36 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Biais et Variance bruit biais Erreur au carré variance 37 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Estimation du biais et de la variance n n n Comment estimer le biais et la variance de g() Pour ce faire, on divise notre corpus d’entraînement en M parties M échantillons Xi={xti , rti}, i=1, . . . , M sont utilisés pour ajuster gi (x), i =1, . . . , M 38 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Dilemne du Biais et de la Variance n n Exemple: ¨ gi(x)=2 n’a pas de variance et un gros biais ¨ gi(x)= ∑t rti/N a un petit biais avec variance Quand la complexité ↑ i. e. ordre polynomiale ↑: biais ↓ (meilleur ajustement des données) ¨ variance ↑ (ajustement varie plus avec les données) ¨ n Dilemne Biais/Variance(Geman et al. , 1992) 39 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

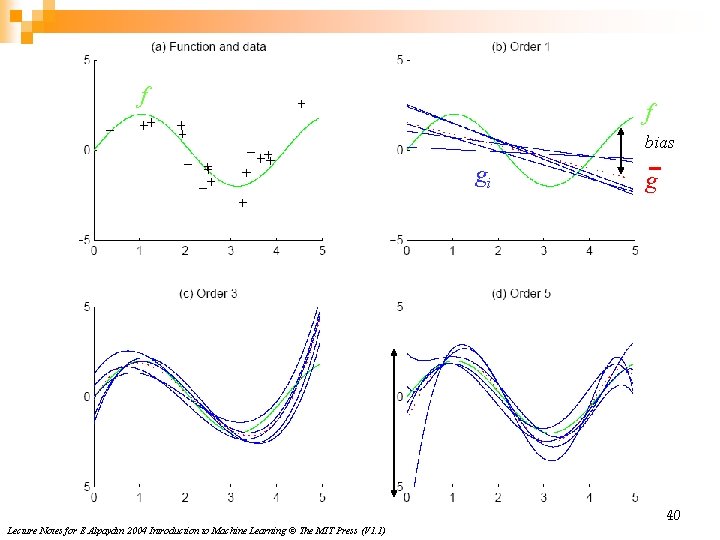
f f bias gi g 40 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

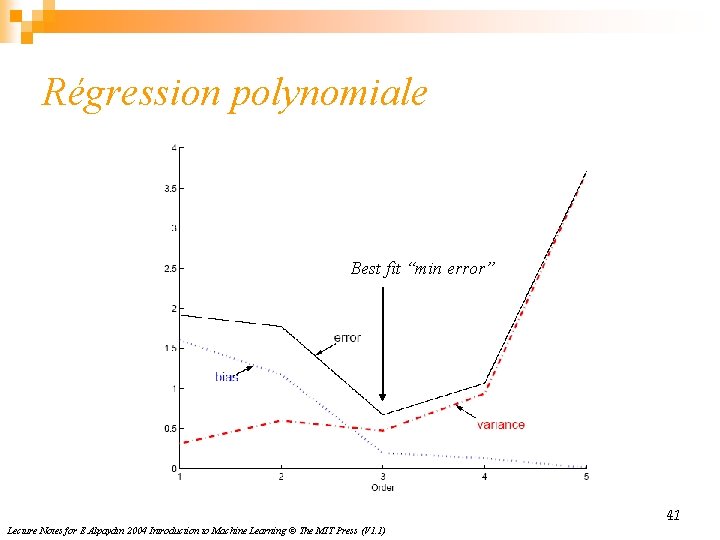
Régression polynomiale Best fit “min error” 41 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)