Lecture 7 Semantic Analysis Xiaoyin Wang CS 5363

Lecture 7 Semantic Analysis Xiaoyin Wang CS 5363 Programming Languages and Compilers

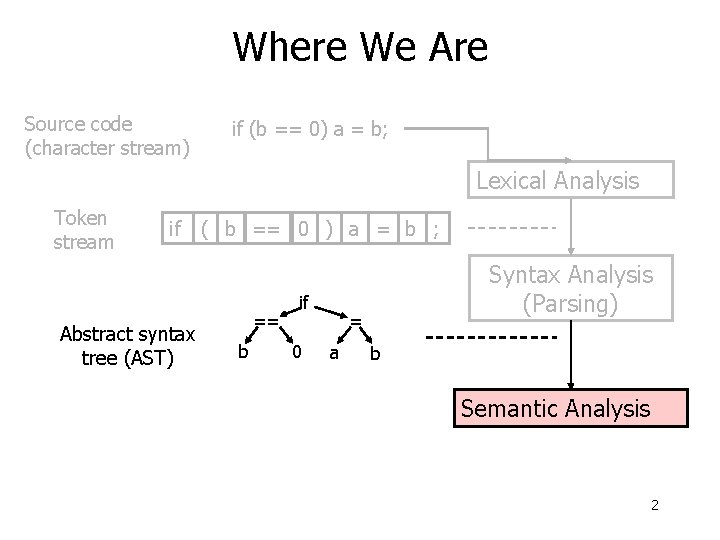
Where We Are Source code (character stream) if (b == 0) a = b; Lexical Analysis Token stream if Abstract syntax tree (AST) ( b == 0 ) a = b ; == b if 0 Syntax Analysis (Parsing) = a b Semantic Analysis 2

AST Decoration • Before performing code generation, we should do some preparation in the AST Level – Static Code Analysis, e. g. , type inference, undefined variables, etc. – Scope Analysis, e. g. , global, class, function, smaller compilation scopes – Symbol Table to support the analyses

AST Data Structure abstract class Expr { } class Add extends Expr {. . . Expr e 1, e 2; } class Num extends Expr {. . . int value; } class Id extends Expr {. . . String name; } 4

Could add AST Analysis to class, but… abstract class Expr { …; /* state variables for visit. A */ } class Add extends Expr {. . . Expr e 1, e 2; void visit. A(){ …; visit. A(this. e 1); …; visit. A(this. e 2); …} } class Num extends Expr {. . . int value; void visit. A(){…} } class Id extends Expr {. . . String name; void visit. A(){…} } 5

Undesirable Approach to AST Analysis abstract class Expr { …; /* state variables for visit. A */ …; /* state variables for visit. B */ } class Add extends Expr {. . . Expr e 1, e 2; void visit. A(){ …; visit. A(this. e 1); …; visit. A(this. e 2); …} void visit. B(){ …; visit. B(this. e 2); …; visit. B(this. e 1); …} } class Num extends Expr {. . . int value; void visit. A(){…} void visit. B(){…} } class Id extends Expr {. . . String name; void visit. A(){…} void visit. B(){…} } 6

Undesirable Approach to AST Computation • The problem with this approach is incorporating different semantic actions into the classes. – Type checking – Code generation – Optimization • Each class would have to implement each “action” as a separate method. 7

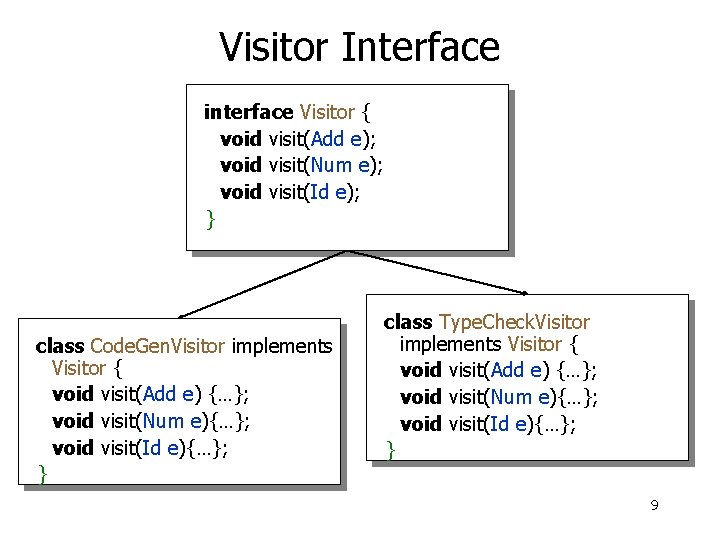
Visitor Methodology for AST Traversal • Visitor pattern: separate data structure definition (e. g. , AST) from algorithms that traverse the structure (e. g. , name resolution code, type checking code, etc. ). • Define Visitor interface for all AST traversals types. • i. e. , code generation, type checking etc. • Extend each AST class with a method that accepts any Visitor (by calling it back) • Code each traversal as a separate class that implements the Visitor interface 8

Visitor Interface interface Visitor { void visit(Add e); void visit(Num e); void visit(Id e); } class Code. Gen. Visitor implements Visitor { void visit(Add e) {…}; void visit(Num e){…}; void visit(Id e){…}; } class Type. Check. Visitor implements Visitor { void visit(Add e) {…}; void visit(Num e){…}; void visit(Id e){…}; } 9

Accept methods abstract class Expr { … abstract public void accept(Visitor v); } class Add extends Expr { … public void accept(Visitor v) { v. visit(this); } } class Num extends Expr { … public void accept(Visitor v) { v. visit(this); } } class Id extends Expr { … public void accept(Visitor v) { v. visit(this); } } The declared type of this is the subclass in which it occurs. Overload resolution of v. visit(this); invokes appropriate visit function in Visitor v. 10

Visitor Methods • For each kind of traversal, implement the Visitor interface, e. g. , class Postfix. Output. Visitor implements Visitor { void visit(Add e) { e. e 1. accept(this); e. e 2. accept(this); System. out. print( “+” ); } Dynamic dispatch e’. accept void visit(Num e) { System. out. print(e. value); invokes accept method of appropriate AST subclass and } void visit(Id e) { eliminates case analysis on System. out. print(e. id); AST subclasses } } • To traverse expression e: Postfix. Output. Visitor v = new Postfix. Output. Visitor(); e. accept(v); 11

Visitor Interface (2) interface Visitor { Object visit(Add e, Object inh); Object visit(Num e, Object inh); Object visit(Id e, Object inh); } 12

Semantic Analysis/Checking Semantic analysis: the final part of the analysis half of compilation – afterwards comes the synthesis half of compilation Purposes: • perform final checking of legality of input program, “missed” by lexical and syntactic checking • name resolution, type checking, break stmt in loop, . . . • “understand” program well enough to do synthesis • Typical goal: relate assignments to & references of particular variable

Types • What is a type? – The notion varies from language to language • Consensus – A set of values – A set of operations on those values • Classes are one instantiation of the modern notion of type

Why Do We Need Type Systems? Consider the assembly language fragment add $r 1, $r 2, $r 3 What are the types of $r 1, $r 2, $r 3?

Types and Operations • Most operations are legal only for values of some types – It doesn’t make sense to add a function pointer and an integer in C – It does make sense to add two integers – But both have the same assembly language implementation!

Type Systems • A language’s type system specifies which operations are valid for which types • The goal of type checking is to ensure that operations are used with the correct types – Enforces intended interpretation of values, because nothing else will! • Type systems provide a concise formalization of the semantic checking rules

What Can Types do For Us? • Can detect certain kinds of errors • Arithmetic errors • Memory errors: – Reading from an invalid pointer, etc. – Calling methods from wrong object

Type Checking Overview • Three kinds of languages: – Statically typed: All or almost all checking of types is done as part of compilation (C, Java, Cool) – Dynamically typed: Almost all checking of types is done as part of program execution (Scheme, Python) – Untyped: No type checking (machine code)

Type Inference • Type Checking is the process of checking that the program obeys the type system • Often involves inferring types for parts of the program – Some people call the process type inference when inference is necessary

Why Rules of Inference? • Inference rules have the form If Hypothesis is true, then Conclusion is true • Type checking computes via reasoning If E 1 and E 2 have certain types, then E 3 has a certain type • Rules of inference are a compact notation for “If. Then” statements

From English to an Inference Rule • The notation is easy to read (with practice) • Start with a simplified system and gradually add features • Building blocks – Symbol Þ is “if-then” – x: T is “x has type T”

Notation for Inference Rules • By tradition inference rules are written Hypothesis 1 … Hypothesisn |- Conclusion • Type rules have hypotheses and conclusions of the form: e : T • means “we can prove that. . . ”

Two Rules |- 3 : Int [Int] (3 is an integer) |- e 1 : Int |- e 2 : Int |- e 1 + e 2 : Int [Add]

Two Rules (Cont. ) • These rules give templates describing how to type integers and + expressions • By filling in the templates, we can produce complete typings for expressions • We can fill the template with ANY expression! |- true : Int |- false : Int |- true + false : Int

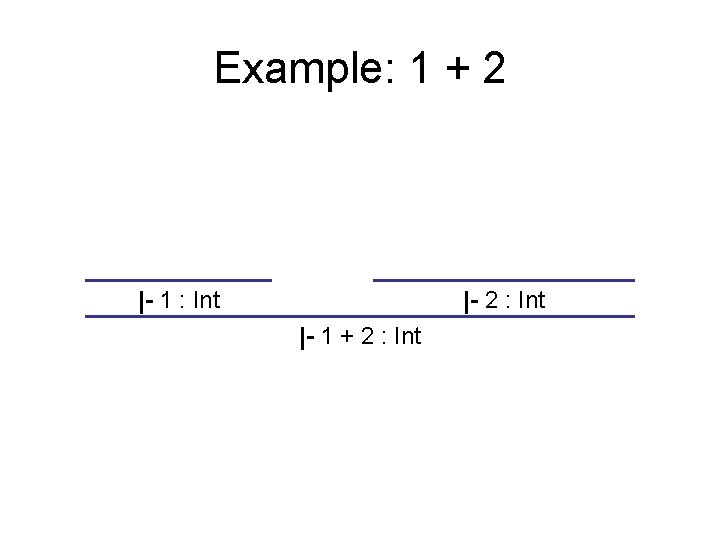
Example: 1 + 2 |- 1 : Int |- 2 : Int |- 1 + 2 : Int

Soundness • A type system is sound if – Whenever |- e : T – Then e evaluates to a value of type T • We only want sound rules – But some sound rules are better than others; here’s one that’s not very useful: |- i : Any (i is an integer)

Type Checking Proofs • Type checking proves facts e : T – One type rule is used for each kind of expression • In the type rule used for a node e: – The hypotheses are the proofs of types of e’s subexpressions – The conclusion is the proof of type of e

Rules for Constants |- False : Bool |- s : String [Bool] [String] (s is a string constant)

Object Creation Example |- T() : T [New] (T denotes a class with parameterless constructor)

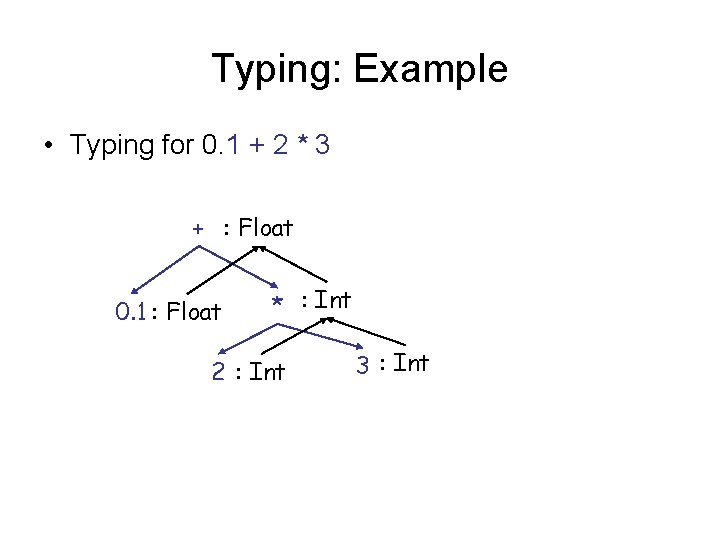
Typing: Example • Typing for 0. 1 + 2 * 3 + : Float 0. 1 : Float * : Int 2 : Int 3 : Int

Typing Derivations • The typing reasoning can be expressed as a tree: |- 2 : Int |- 3 : Int |- 2 * 3 : Int |- 1 + 2 * 3: Int • The root of the tree is the whole expression • Each node is an instance of a typing rule • Leaves are the rules with no hypotheses

A Problem • What is the type of a variable reference? |- x : ? [Var] (x is an identifier) • This rules does not have enough information to give a type. – We need a hypothesis of the form “we are in the scope of a declaration of x with type T”)

A Solution: Put more information in the rules! • A type environment gives types for free variables – A type environment is a mapping from Identifiers to Types – A variable is free in an expression if: • The expression contains an occurrence of the variable that refers to a declaration outside the expression

Type Environments Let O be a function from Identifiers to Types The sentence O |- e : T is read: Under the assumption that variables in the current scope have the types given by O, it is provable that the expression e has the type T

Modified Rules The type environment is added to the earlier rules: [Int] O |- e : Int O |- write. Int e : void O |- e 1 : Int O |- e 2 : Int O |- e 1 + e 2 : Int (i is an integer) [Add]

New Rules And we can write new rules: O |- x : T [Var] (if O(x) = T)

Subtyping • Define a relation X Y on classes to say that: – An object of type X could be used when one of type Y is acceptable, or equivalently – X conforms with Y – This means that X is a subclass of Y

Dynamic And Static Types • The dynamic type of an object is the class C that is used in the “new C” expression that creates the object – A run-time notion – Even languages that are not statically typed have the notion of dynamic type • The static type of an expression is a notion that captures all possible dynamic types the expression could take – A compile-time notion

Dynamic and Static Types. (Cont. ) • In early type systems the set of static types correspond directly with the dynamic types • Soundness theorem: for all expressions E dynamic_type(E) = static_type(E) (in all executions, E evaluates to values of the type inferred by the compiler) • This gets more complicated in advanced type systems

Dynamic and Static Types x has static type A class A extends Object: … class B extends A: … def Main(): Here, x’s value has x: A dynamic type A x = A() … x B() Here, x’s value has dynamic type B … • A variable of static type A can hold values of static type B, if B A

Dynamic and Static Types Soundness theorem: " E. dynamic_type(E) <= static_type(E) Why is this Ok? – For E, compiler uses static_type(E) (call it C) – All operations that can be used on an object of type C can also be used on an object of type C’ C • Such as fetching the value of an attribute • Or invoking a method on the object – Subclasses can only add attributes or methods – Methods can be redefined but with same type !

Assignment More uses of subtyping: To the left, rule for languages with assignment expressions; to the right, assignment statements O |- id : T 0 O |- e 1 : T 1 T 0 O |- id = e 1 : T 1 O |- id : T 0 O |- e 1 : T 1 T 0 O |- id = e 1; : void

Conditional Expression • Consider: e 0 ? e 1 : e 2 in C • The result can be either e 1 or e 2 • The dynamic type is either e 1’s or e 2’s type • The best we can do statically is the smallest supertype larger than the type of e 1 and e 2

If-Then-Else example • Consider the class hierarchy P A B • … and the expression C? new A : new B • Its type should allow for the dynamic type to be both A or B – Smallest supertype is P

Least Upper Bounds • lub(X, Y), the least upper bound of X and Y, is Z if – X Z Ù Y Z Z is an upper bound – X Z’ Ù Y Z’ Þ Z Z’ Z is least among upper bounds • Typically, the least upper bound of two types is their least common ancestor in the inheritance tree

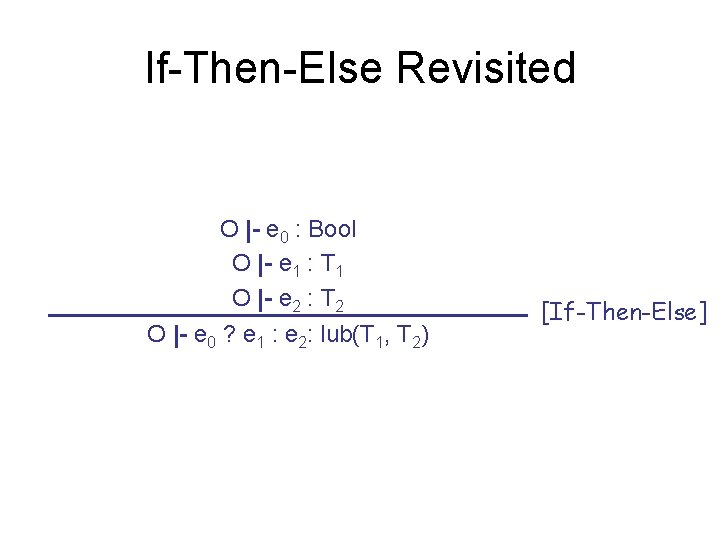
If-Then-Else Revisited O |- e 0 : Bool O |- e 1 : T 1 O |- e 2 : T 2 O |- e 0 ? e 1 : e 2: lub(T 1, T 2) [If-Then-Else]

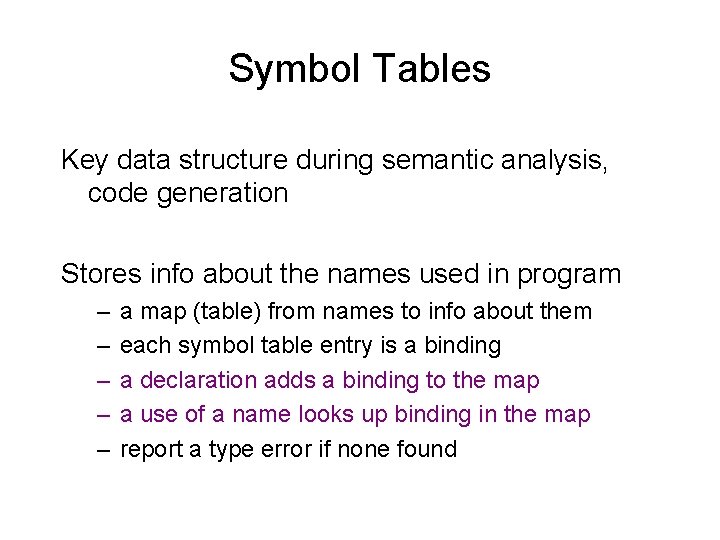
Symbol Tables Key data structure during semantic analysis, code generation Stores info about the names used in program – – – a map (table) from names to info about them each symbol table entry is a binding a declaration adds a binding to the map a use of a name looks up binding in the map report a type error if none found

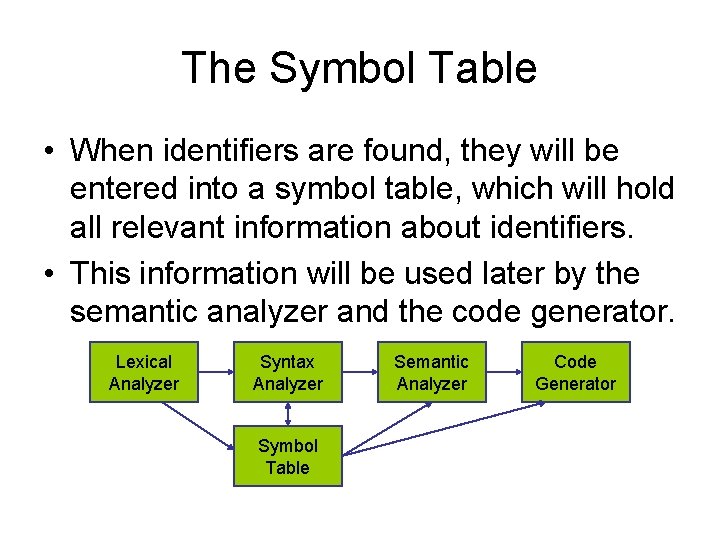
The Symbol Table • When identifiers are found, they will be entered into a symbol table, which will hold all relevant information about identifiers. • This information will be used later by the semantic analyzer and the code generator. Lexical Analyzer Syntax Analyzer Symbol Table Semantic Analyzer Code Generator

Symbol Table Entries • We will store the following information about identifiers. • • • The name (as a string). The data type. The block level. Its scope (global, local, or parameter). Its offset from the base pointer (for local variables and parameters only).

Symbol Table Entries • This information is stored in an object called an Id. Entry. • This information may not all be known at once. • We may begin by knowing only the name and data type, and then later learn the block level, scope, and the offset.

Symbol Table Functions • The two most basic symbol-table functions are the ones that insert a new symbol and lookup an old symbol. – Id. Entry install(String s, int blk. Lev) – Id. Entry id. Lookup(String s, int blk. Lev)

Inserting a Symbol • The install() function will insert a new symbol into the symbol table. • Each symbol has a block level. – Block level 1 = Global variables. – Block level 2 = Parameters and local variables. • install() will create an Id. Entry object and store it in the table.

Inserting a Symbol • When the symbol is first encountered by the semantic analyzer, we do not yet know the scope or type. • For example, we could first encounter the symbol count in any of the following contexts. – int count; // Global variable – int func(int sum, float count); – int main() {int count…}

Looking up a Symbol • Whenever a symbol is encountered, we must look it up in the symbol table. • If it is the first encounter, then id. Lookup() will return null. • If it is not the first encounter, then id. Lookup() will return a reference to the Id. Entry for that identifier found in the table. • Once we have the Id. Entry object, we may add information to it.

Looking up a Symbol • Since a variable should be declared when it first appears, – If the semantic analyzer is analyzing a declaration, then it expects id. Lookup() to return null. – If the semantic analyzer is not analyzing a declaration, then it expects id. Lookup() to return non-null. – In each case, anything else is an error.

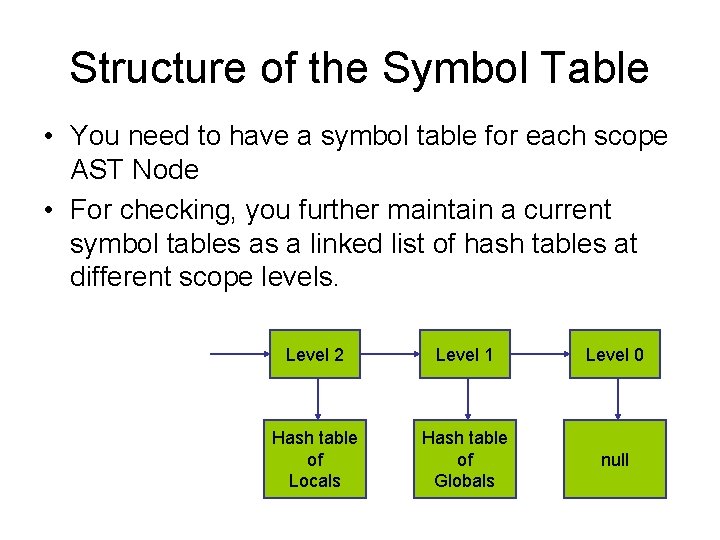
Structure of the Symbol Table • You need to have a symbol table for each scope AST Node • For checking, you further maintain a current symbol tables as a linked list of hash tables at different scope levels. Level 2 Level 1 Level 0 Hash table of Locals Hash table of Globals null

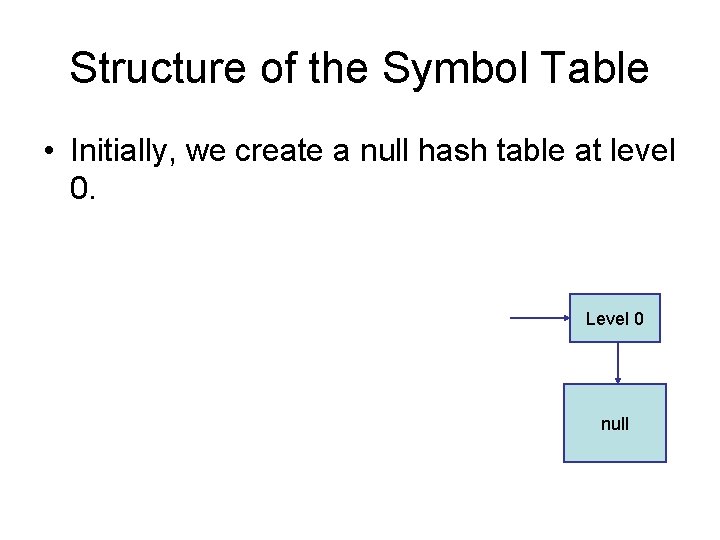
Structure of the Symbol Table • Initially, we create a null hash table at level 0. Level 0 null

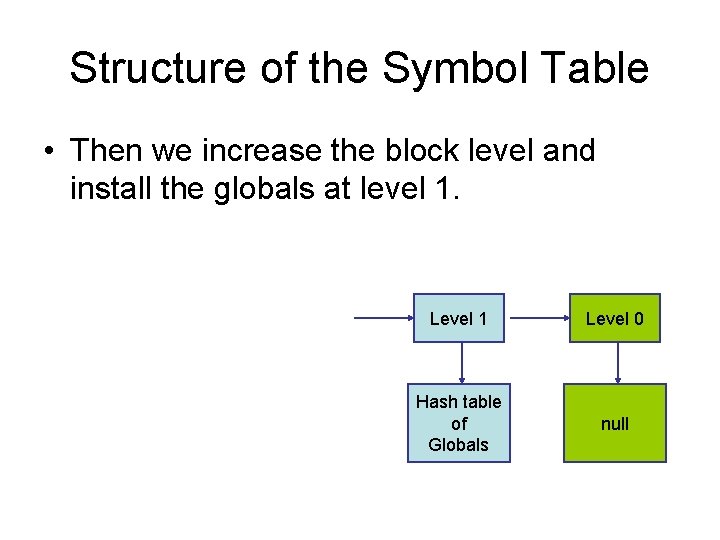
Structure of the Symbol Table • Then we increase the block level and install the globals at level 1. Level 1 Level 0 Hash table of Globals null

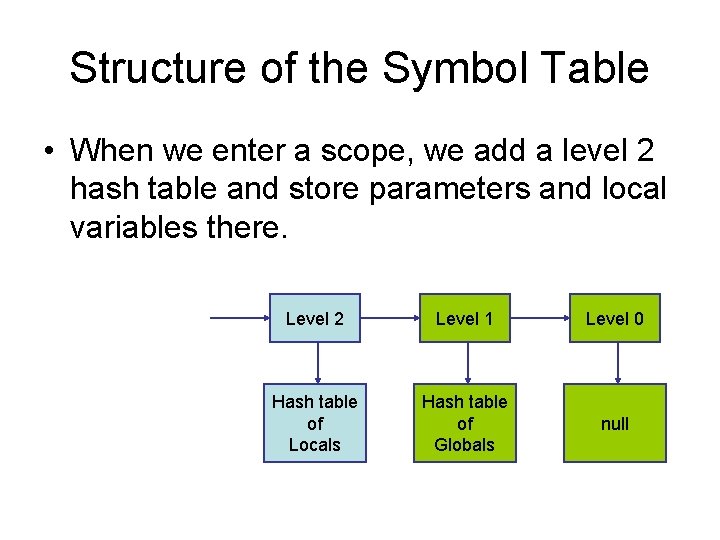
Structure of the Symbol Table • When we enter a scope, we add a level 2 hash table and store parameters and local variables there. Level 2 Level 1 Level 0 Hash table of Locals Hash table of Globals null

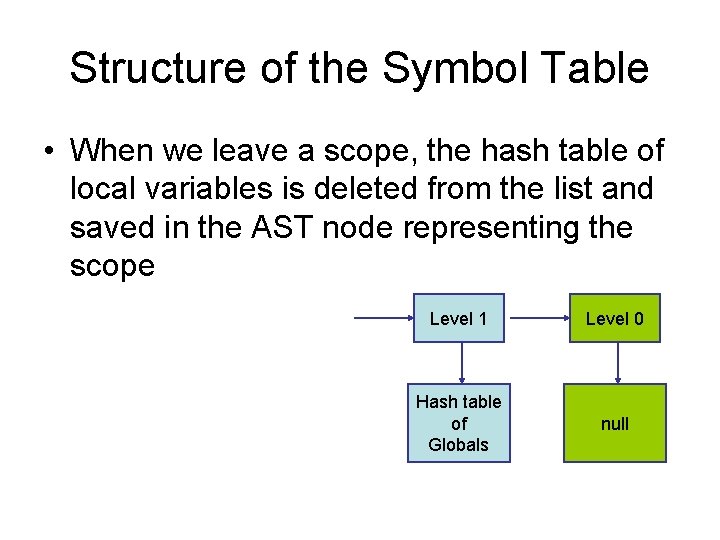
Structure of the Symbol Table • When we leave a scope, the hash table of local variables is deleted from the list and saved in the AST node representing the scope Level 1 Level 0 Hash table of Globals null

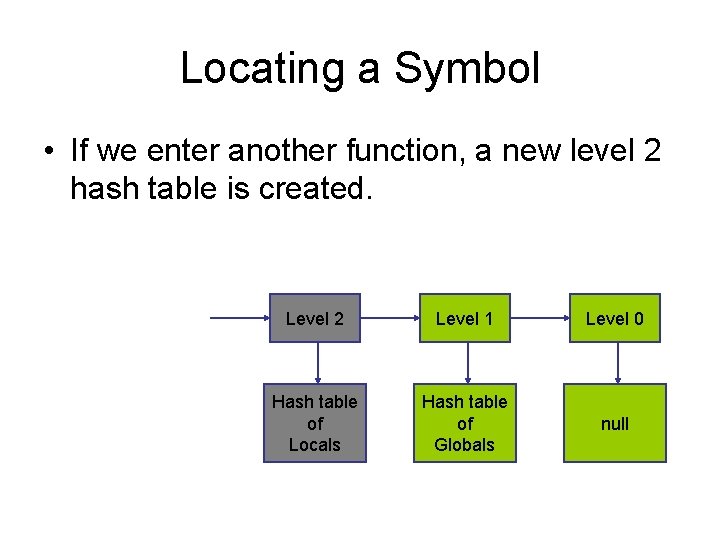
Locating a Symbol • If we enter another function, a new level 2 hash table is created. Level 2 Level 1 Level 0 Hash table of Locals Hash table of Globals null

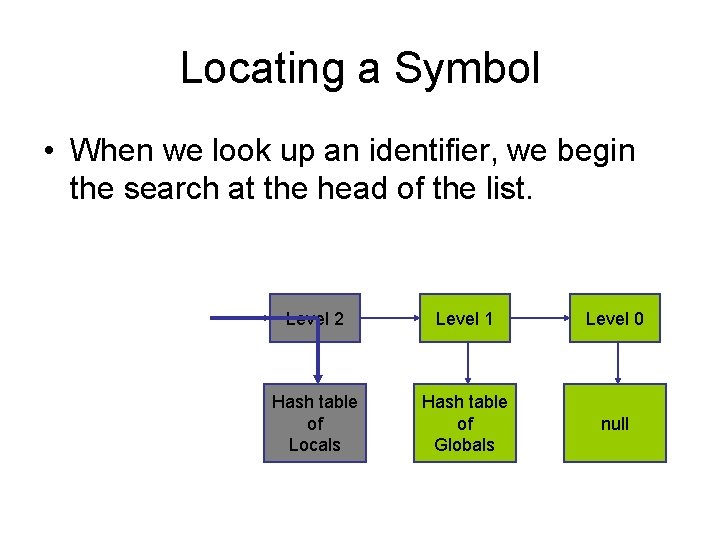
Locating a Symbol • When we look up an identifier, we begin the search at the head of the list. Level 2 Level 1 Level 0 Hash table of Locals Hash table of Globals null

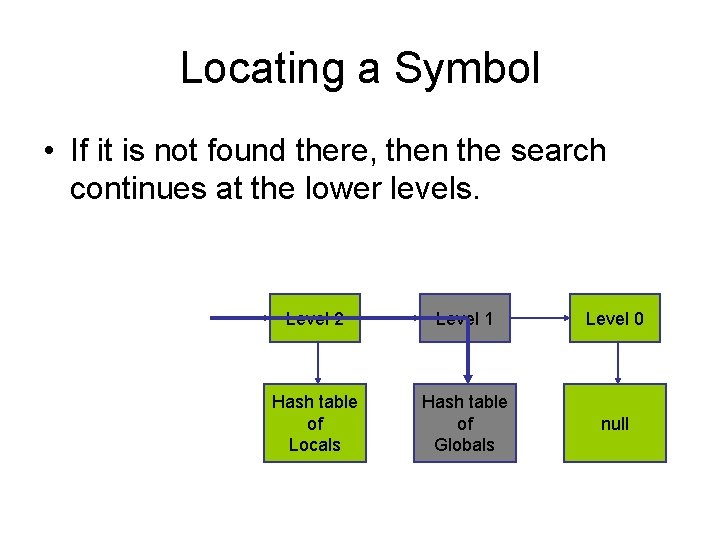
Locating a Symbol • If it is not found there, then the search continues at the lower levels. Level 2 Level 1 Level 0 Hash table of Locals Hash table of Globals null

Looking up a Symbol • If an identifier is declared both globally and locally, which one will be found when it is looked up? • If an identifier is declared only globally and we are in a function, how will it be found? • How do we prevent the use of a keyword as a variable name?

String Tables • Compilers generally create a table of strings. • These strings are the “names” of the identifiers, keywords, and other strings used in the program. • Thus, if the same string is used for several different identifiers, the string will be stored only once in the string table. • Each symbol table entry will include a pointer to the string in the string table. • For simplicity, we will not use a string table.

Semantic Analysis in Multiple Rounds • Symbol Table Construction – Names – Signatures – Bodies • Type Checking

Semantic Analysis in Multiple Rounds class A{ int f(B b){ return b. x() + t; } int t; } class B{ int x(){ return 1; } }