KONSEP DASAR FUNGSI DAN GRAFIK KONSEP DASAR FUNGSI


















- Slides: 26

KONSEP DASAR FUNGSI DAN GRAFIK

KONSEP DASAR FUNGSI DAN GRAFIK Definisi : Fungsi (memadankan) setiap Notasi : Ilustrasi : adalah suatu aturan yang mengaitkan dengan tepat satu f : A B x y = f (x) A B f Gambar fungsi y = f(x)

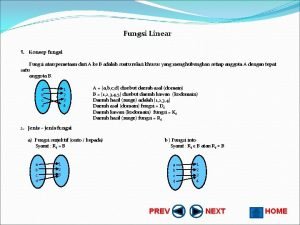
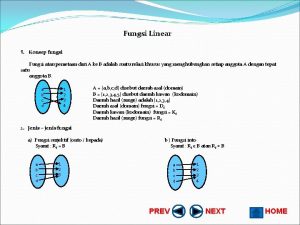
ILUSTRASI FUNGSI Definisi : Misalkan A dan B dua himpunan takkosong. Fungsi dari A ke B adalah aturan yang mengaitkan setiap anggota A dengan tepat satu anggota B. ATURAN : setiap anggota A harus habis terpasang dengan anggota B. tidak boleh membentuk cabang seperti ini. A B

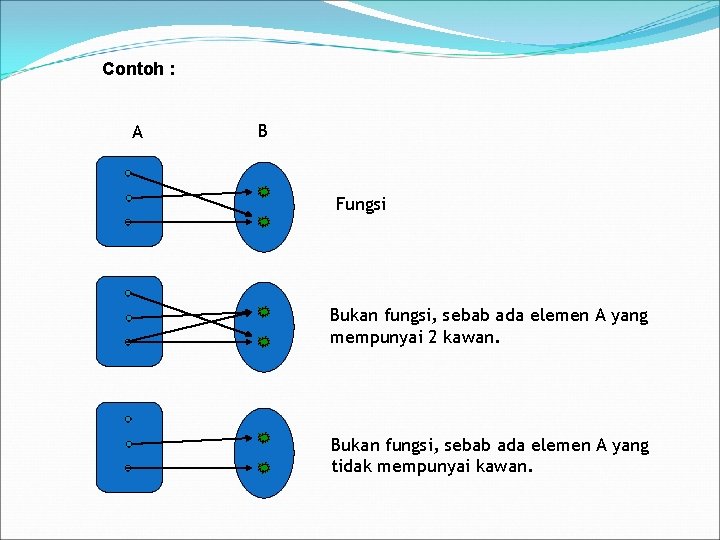
Contoh : A B Fungsi Bukan fungsi, sebab ada elemen A yang mempunyai 2 kawan. Bukan fungsi, sebab ada elemen A yang tidak mempunyai kawan.

Domain / daerah asal dari f(x), notasi Df , yaitu Daerah nilai / Range /Kodomain dari f(x) , notasi Rf , yaitu Himpunan titik di bidang, disebut grafik fungsi f Contoh : Misalkan , maka f(1) = 8, f(-2) = 5 Misalkan , maka 5

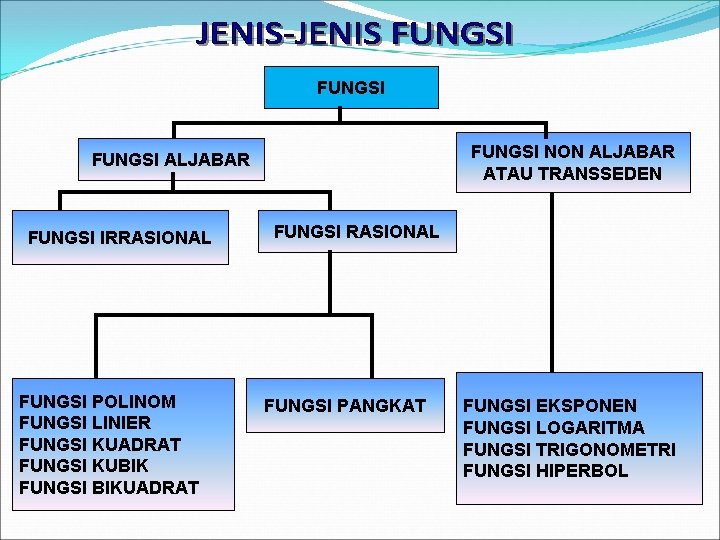
FUNGSI NON ALJABAR ATAU TRANSSEDEN FUNGSI ALJABAR FUNGSI IRRASIONAL FUNGSI POLINOM FUNGSI LINIER FUNGSI KUADRAT FUNGSI KUBIK FUNGSI BIKUADRAT FUNGSI RASIONAL FUNGSI PANGKAT FUNGSI EKSPONEN FUNGSI LOGARITMA FUNGSI TRIGONOMETRI FUNGSI HIPERBOL

FUNGSI IRRASIONAL : Y = ( 1 + 2 X – 3 X 2 + 4 X 3 + … + 12 X 11) 1/11 (Fungsi yang memiliki bentuk umum dimana n aalah bilangan bulat positif) FUNGSI POLINOM : Y = 1 + 2 X – 3 X 2 + 4 X 3 + …+ 12 X 11 FUNGSI LINIER : Y = 1 + 2 X FUNGSI KUADRAT : Y = 1 + 2 X – 3 X 2 FUNGSI KUBIK : Y = 1 + 2 X – 3 X 2 + 4 X 3 FUNGSI BIKUADRAT : Y = 1 + 2 X – 3 X 2 + 4 X 3 + 5 X 4 (Fungsi polinom yang variabel bebasnya memiliki pangkat paling tinggi adalah empat) FUNGSI PANGKAT : Y = X n , n = bulat positif FUNGSI EKSPONEN : Y = 2 X FUNGSI LOGARITMA : Y = n Log X FUNGSI HIPERBOLA : Y = X n , n = riil negatif

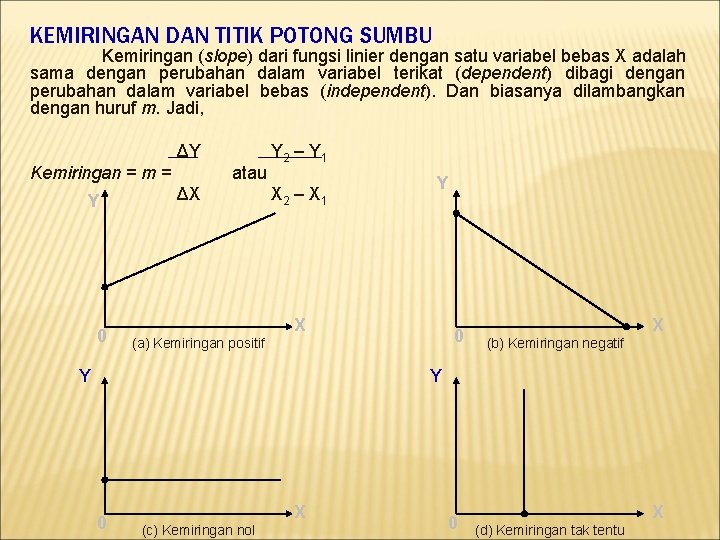
KEMIRINGAN DAN TITIK POTONG SUMBU Kemiringan (slope) dari fungsi linier dengan satu variabel bebas X adalah sama dengan perubahan dalam variabel terikat (dependent) dibagi dengan perubahan dalam variabel bebas (independent). Dan biasanya dilambangkan dengan huruf m. Jadi, ΔY Kemiringan = m = Y 0 atau ΔX Y 2 – Y 1 X 2 – X 1 Y X 0 (a) Kemiringan positif Y X (b) Kemiringan negatif Y 0 X (c) Kemiringan nol 0 X (d) Kemiringan tak tentu

BENTUK UMUM FUNGSI LINIER Y=a 0 + a 1 X di mana a, tidak sama dengan nol. Bentuk ini disebut sebagai bentuk kemiringantitik potong (slope-intercept). Bentuk seperti ini bila dilihat dari letak kedua variabel X dab Y, maka bentuk ini dapat disebut sebagai eksplisit. Karena variabel bebas X dan variabel terikat Y saling terpisah oleh tanda sama dengan (=)

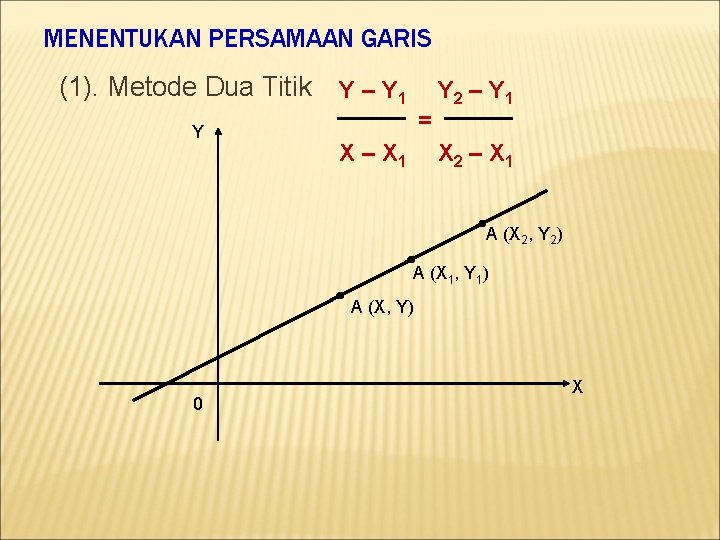
MENENTUKAN PERSAMAAN GARIS (1). Metode Dua Titik Y Y – Y 1 = X – X 1 Y 2 – Y 1 X 2 – X 1 A (X 2, Y 2) A (X 1, Y 1) A (X, Y) 0 X

Carilah persamaan garis yang melalui titik (3, 2) dan (4, 6) Penyelesaian : X 1 = 3, X 2 = 4, Y 1 = 2, dan Y 2 = 6 = Y – Y 1 Y 2 – Y 1 X – X 1 X 2 – X 1 Persamaan garis Y = 4 x - 10 ini grafiknya ditunjukkan oleh gambar 4. 3. Y Y– 2 = 6– 2 X– 3 4– 3 6– 2 Y– 2 = Y– 2 Y Y = 4 (X – 3) = 4 X – 12 = 4 X - 10 4– 3 Y = 4 X - 10 (X – 3) X 0 1 5 (0, -10) 2 3

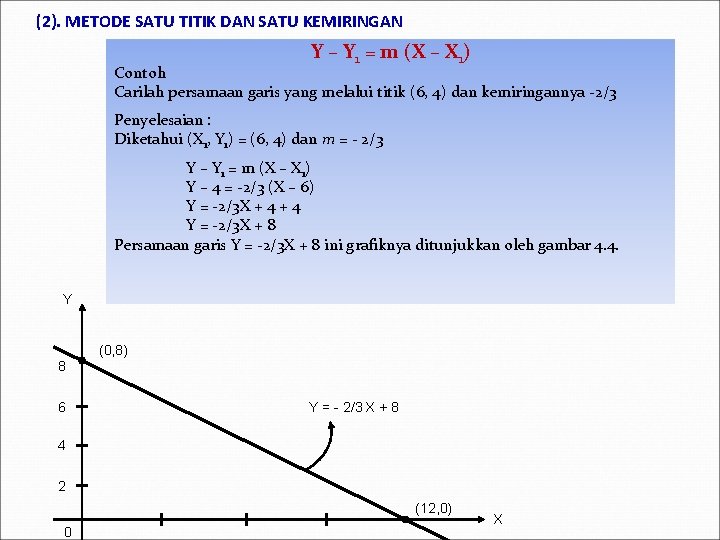
(2). METODE SATU TITIK DAN SATU KEMIRINGAN Y – Y 1 = m (X – X 1) Contoh Carilah persamaan garis yang melalui titik (6, 4) dan kemiringannya -2/3 Penyelesaian : Diketahui (X 1, Y 1) = (6, 4) dan m = - 2/3 Y – Y 1 = m (X – X 1) Y – 4 = -2/3 (X – 6) Y = -2/3 X + 4 Y = -2/3 X + 8 Persamaan garis Y = -2/3 X + 8 ini grafiknya ditunjukkan oleh gambar 4. 4. Y (0, 8) 8 6 Y = - 2/3 X + 8 4 2 (12, 0) 0 X

HUBUNGAN DUA GARIS LURUS y 1=a 0 + a 1 x dan y 2=b 0 + b 1 x Y Y a 1 ≠ b 1 a 1 = b 1 y 1 ao ≠ b 0 y 2 0 X 0 (a) Berpotongan Y Y a 1 = b 1 ao = b 0 X (b) Sejajar a 1. b 1 = -1 y 1 ao ≠ b 0 y 2 0 X (c) Berimpit 0 X (d) Tegak Lurus

SISTEM PERSAMAAN LINIER PENYELESAIAN SISTEM PERSAMAAN LINIER: DUA PERSAMAAN DENGAN DUA VARIABEL METODE ELIMINASI Contoh 5. 1. Carilah nilai-nilai dari variabel X dan Y yang dapat memenuhi kedua persamaan berikut ini : 3 X – 2 Y = 7 (5. 1) 2 X + 4 Y = 10 (5. 2) Penyelesaian : 1. Variabel yang akan dieliminasikan adalah variabel Y. 2. Karena variabel Y yang dipilih, maka Persamaan (5. 1) harus dikalikan dengan konstanta 2, dan Persamaan (5. 2) dikalikan dengan konstanta 1, sehingga kedua persamaan menjadi, 3 X – 2 Y = 7 (kalikan dengan 2), maka 6 X – 4 Y = 14 2 X + 4 Y = 10 (kalikan dengan 1), maka 2 X + 4 Y = 10 3. Karena kedua koefisien dari variabel Y tandanya berbeda, maka harus dijumlahkan, dan menjadi, 6 X – 4 Y = 14 2 X + 4 Y = 10 + 8 X + 0 = 24 X=3 4. Subtitusikan nilai X = 3 kedalam salah satu persamaan semula agar diperoleh nilai Y. Bila disubtitusikan pada Persamaan (5. 1), maka akan menghasilkan, 3 (3) -2 Y = 7 - 2 Y = 7 – 9 Y=1

METODE SUBSTITUSI Contoh 5. 2. 3 X – 2 Y = 7 2 X + 4 Y = 10 (5. 1) (5. 2) Misalkan variabel X yang dipilih pada persamaan (5. 2), maka akan menjadi, 2 X = 10 – 4 Y X = 5 – 2 Y (koefisien variabel X=1) Karena Persamaan (5. 2)’ yang dipilih, maka subtitusikan kedalam persamaan pertama, sehingga menjadi, 3 (5 – 2 Y) – 2 Y 15 – 6 Y – 2 Y 15 – 8 Y -8 Y Y =7 =7 =7 = 7 – 15 =1 Substitusikan nilai Y = 1 ini kedalam salah satu persamaan mula-mula, misalkan Persamaan (5. 1)’, sehingga memperoleh hasil, 3 X – 2 (1) 3 X X =3 =7 =7+2 Jadi, himpunan penyelesaian yang memenuhi kedua persamaan tersebut adalah himpunan pasangan urut (3. 1).

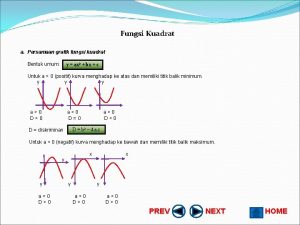
Fungsi Kuadrat Bentuk umum dari fungsi kuadrat adalah y = a x 2 + bx + c D = b 2 – 4 ac Maka, Bentuk grafik dari fungsi kuadrat adalah PARABOLA x 1 x 2 a+ x x 1 x 2 a-

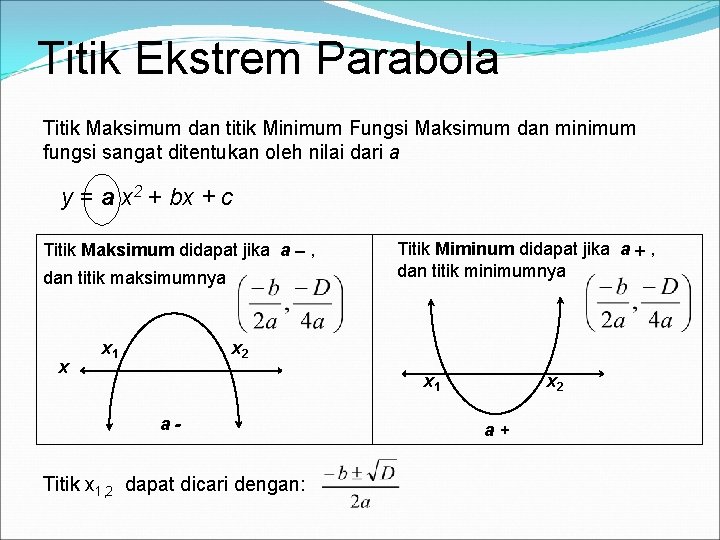
Koordinat titik puncak diperoleh dgn rumus: Titik puncak = -b - (b 2 – 4 ac) ----- , -------2 a 4 a -b ±√ (b 2 – 4 ac) X 1. 2 = ----------2 a Contoh: Jika fungsi kuadrat Y = X 2 – 8 X + 12 Carilah koordinat titik puncak dan gambarkan Koordinat Titik puncak = -b - (b 2 – 4 ac) ----- , -------2 a 4 a

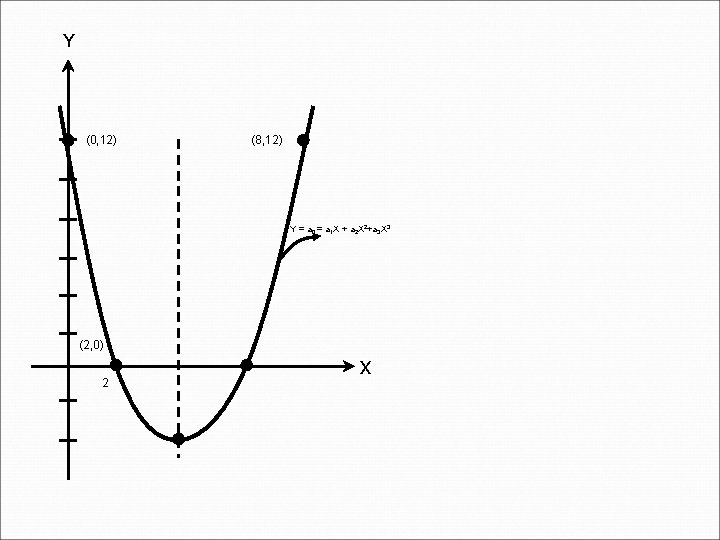
Contoh : Jika fungsi kuadrat Y = X 2 – 8 X + 12, carilah koordinat titik puncak dan gambarkanlah parabolanya? Penyelesaian : Koordinat titik puncak Untuk X = 0, maka Y = 12 Titik potong sumbu Y adalah (0, 12) Untuk Y = 0, maka X 2 – 8 X + 12 = 0

Titik potong sumbu X adalah (2, 0) dan (6, 0). Berdasarkan nilai-nilai penyelesaian dari titik puncak dan titik potong sumbu X dan Y, maka kurva parabolannya dapat digambarkan seperti 7. 3.

Y (0, 12) (8, 12) Y = a 0 = a 1 X + a 2 X 2+a 3 X 3 (2, 0) 2 x

Fungsi Kuadrat Bentuk umum dari fungsi kuadrat adalah y = a x 2 + bx + c D = b 2 – 4 ac Maka, Bentuk grafik dari fungsi kuadrat adalah PARABOLA x 1 x 2 a+ x x 1 x 2 a-

Titik Ekstrem Parabola Titik Maksimum dan titik Minimum Fungsi Maksimum dan minimum fungsi sangat ditentukan oleh nilai dari a y = a x 2 + bx + c Titik Maksimum didapat jika a , dan titik maksimumnya x x 1 Titik Miminum didapat jika a , dan titik minimumnya x 2 x 1 a- Titik x 1, 2 dapat dicari dengan: x 2 a+

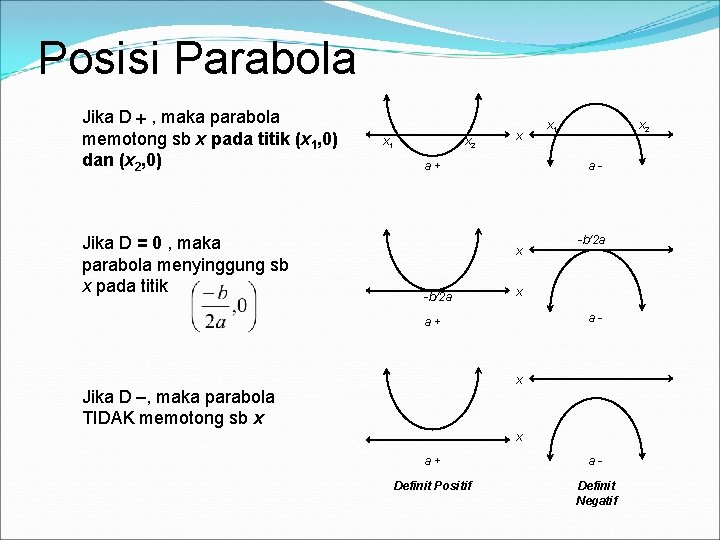
Posisi Parabola Jika D , maka parabola memotong sb x pada titik (x 1, 0) dan (x 2, 0) Jika D = 0 , maka parabola menyinggung sb x pada titik x 1 x 2 x a+ x 2 a- x -b/2 a x 1 -b/2 a x a- a+ x Jika D , maka parabola TIDAK memotong sb x x a+ a- Definit Positif Definit Negatif

FUNGSI PANGKAT TIGA Polinomial tingkat 3 dengan satu variabel bebas disebut sebagai kubik, dan mempunyai bentuk umum : Y = a 0 + a 1 X + a 2 X 2 + a 3 X 3 dimana : a 3 tidak sama dengan nol. fungsi kubik ini bila digambarkan dalam bidang koordinat Cartesius, kurvanya mempunyai dua lengkung (concave) yaitu : lengkung ke atas dan lengkung ke bawah, seperti tampak pada gambar di samping. Y Y = a 0 = a 1 X + a 2 X 2+a 3 X 3 a 0 0 x

PENERAPAN FUNGSI DI BIDANG EKONOMI Fungsi linier adalah suatu fungsi yang sangat sering digunakan oleh para ahli ekonomi dan bisnis dalam menganalisa dan memecahkan masalah-masalah ekonomi. Hal ini dikarenakan bahwa kebanyakan masalah ekonomi dan bisnis dapat disederhanakan atau diterjemahkan ke dalam model yang berbentuk linier.

Beberapa penerapan fungsi linier dalam bidang ekonomi dan bisnis adalah: a. Fungsi permintaan, fungsi penawaran dan keseimbangan pasar b. Keseimbangan Pasar Dua Macam Produk c. Pengaruh Pajak dan Subsidi Terhadap Keseimbangan Pasar. d. Fungsi biaya, fungsi pendapatan dan analisis Pulang Pokok (BEP=Break Even Point) e. Fungsi Konsumsi dan Tabungan f. Model Penentuan Pendapatan Nasional
 Jenis bahan grafik
Jenis bahan grafik Konsep dasar unit pemrosesan dan dasar datapath
Konsep dasar unit pemrosesan dan dasar datapath Datapath
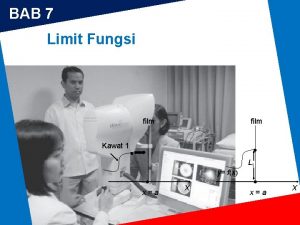
Datapath Film
Film Fungsi linier dan non linier
Fungsi linier dan non linier Etika desain
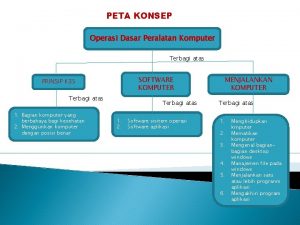
Etika desain Peta konsep tentang komputer
Peta konsep tentang komputer Rumus trigonometri kelas 10
Rumus trigonometri kelas 10 Metode satu titik dan satu kemiringan
Metode satu titik dan satu kemiringan Dasar grafik 2d pada java
Dasar grafik 2d pada java Pengukuran dan teori ketidakpastian
Pengukuran dan teori ketidakpastian Dasar dasar dan perlakuan adil di tempat kerja
Dasar dasar dan perlakuan adil di tempat kerja Contoh soal fungsi transenden
Contoh soal fungsi transenden Konsep dasar profesi kependidikan
Konsep dasar profesi kependidikan Konsep ekonomi internasional
Konsep ekonomi internasional Konsep dasar komunikasi
Konsep dasar komunikasi Konsep konsep dasar akuntansi manajemen
Konsep konsep dasar akuntansi manajemen Konsep dasar wirausaha
Konsep dasar wirausaha Grafik pencerminan
Grafik pencerminan Persamaan sin cos
Persamaan sin cos Grafik limit
Grafik limit Contoh soal grafik fungsi aljabar
Contoh soal grafik fungsi aljabar Selang kelengkungan kurva
Selang kelengkungan kurva Frequency of a cos function
Frequency of a cos function Apa itu fungsi penerimaan
Apa itu fungsi penerimaan Bentuk grafik fungsi kuadrat
Bentuk grafik fungsi kuadrat Fungsi periodik adalah
Fungsi periodik adalah