DERET FOURIER Fungsi Periodik Fungsi fx dikatakan periodik









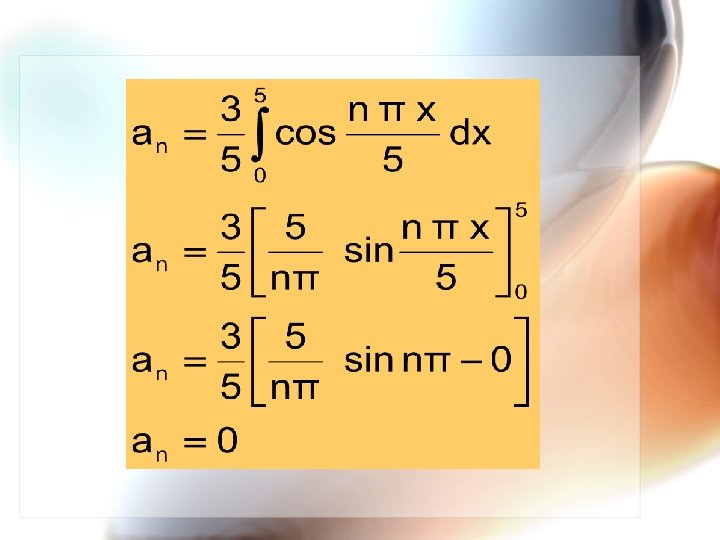

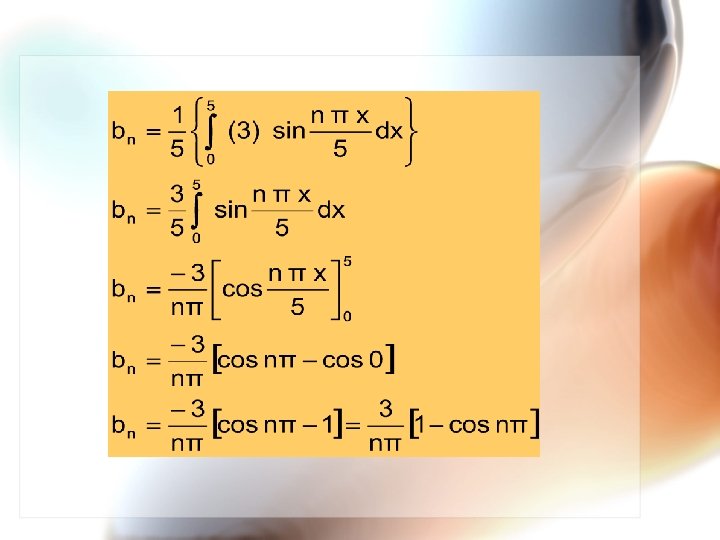
















- Slides: 33

DERET FOURIER:

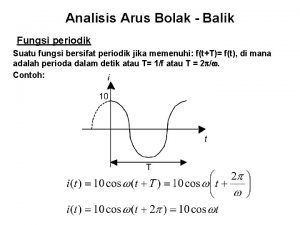
Fungsi Periodik Fungsi f(x) dikatakan periodik dengan perioda T, jika untuk semua harga x berlaku: f(x+T) = f(x); T adalah konstanta positif Harga terkecil dari T > 0 disebut perioda terkecil atau disebut perioda dari f(x).

Contoh: • Fungsi sin x mempunyai periode 2 , 4 , 6 , …karena sin (x+2 ) = sin (x+4 )= sin (x+6 ) =…=sin x • Periode dari sin nx atau cos nx: dengan n bilangan bulat positif adalah 2 /n • Periode dari tan x adalah • Fungsi konstan mempunyai periode sembarang bilangan positif

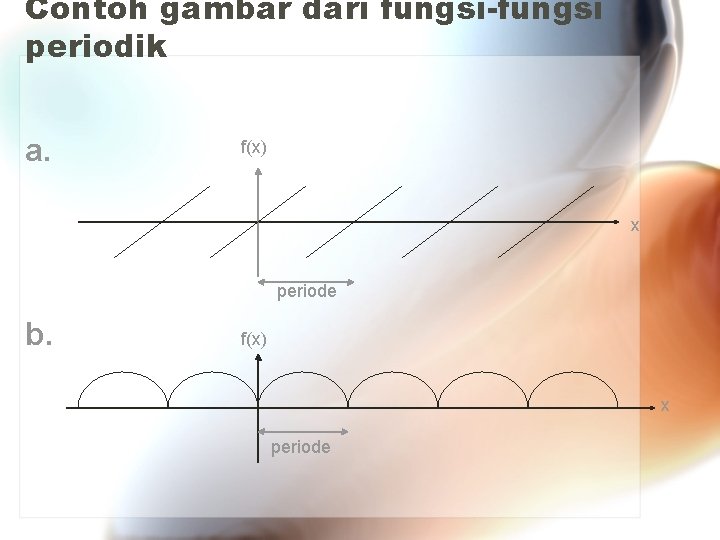
Contoh gambar dari fungsi-fungsi periodik a. f(x) x periode b. f(x) x periode

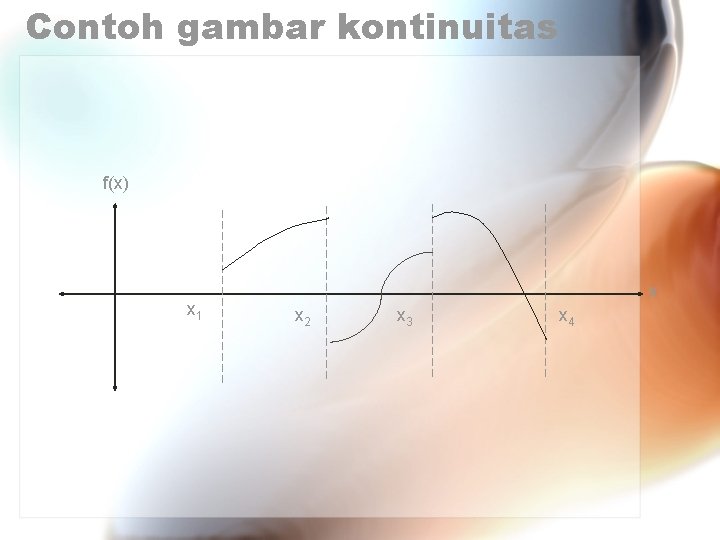
Kontinuitas Fungsi f(x) dikatakan kontinu pada setiap segmen (piecewise continuous function), bila f(x) hanya kontinu pada interval tertentu dan diskontinu pada titik -titik yang banyaknya berhingga. Harga f(x) di titik-titik diskontinu ditentukan dengan menghitung harga limit fungsi f(x) untuk x mendekati titik diskontinu (ujung masing-masing interval)

Contoh gambar kontinuitas f(x) x 1 x x 2 x 3 x 4

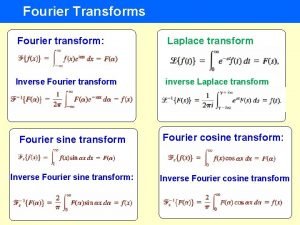
Definisi Deret Fourier Jika fungsi f(x) terdefinisi pada interval (-L, L) dan diluar interval tersebut f(x) periodik dengan periode 2 L, maka Deret Fourier atau Ekspansi Fourier dari fungsi f(x) tersebut didefinisikan sebagai berikut:

dengan koefisien Fourier an, bn ditentukan oleh:

Jika interval (-L, L) sembarang dan f(x) mempunyai periode 2 L maka dengan C sembarang bilangan real. Jika C=-L maka rumus (4) dan (5) akan sama dengan (2) dan (3).

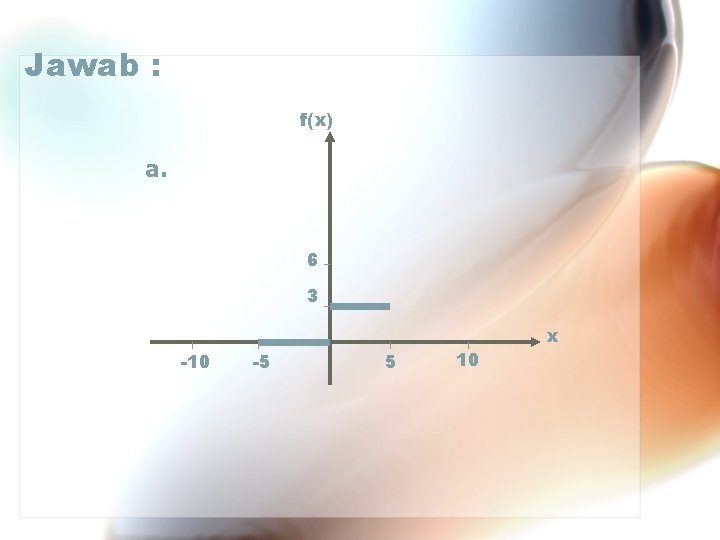
CONTOH : 0 -5<x<0 f(x)= periode = 10 3 0<x<5 a. Gambarkan f(x) diatas ! b. Tentukan koefisien Fourier an dan bn! c. Tuliskan deret Fourier ! d. Uraikan deret Fourier !

Jawab : f(x) a. 6 3 -10 -5 5 10 x

b. Periode 2 L L = = = 10 10 5
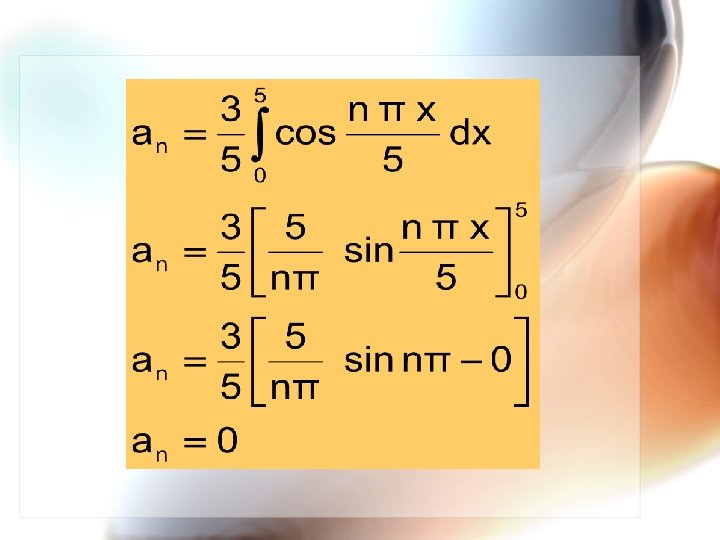

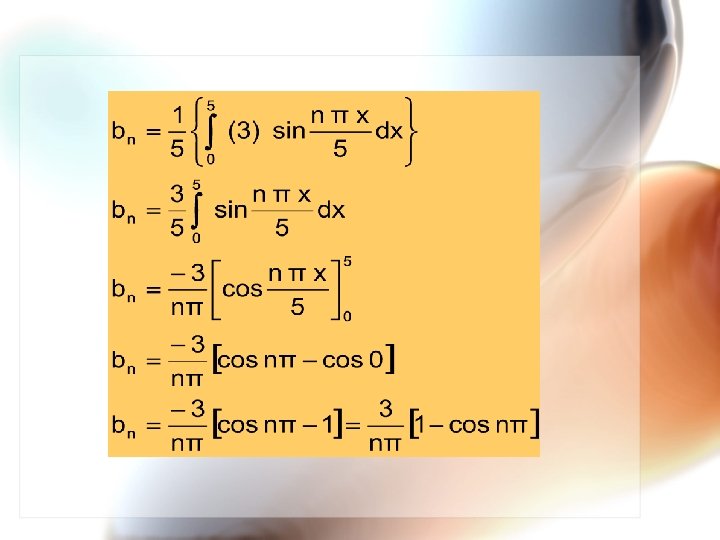

c. Deret Fourier

d. Uraian Deret Fourier

Syarat / Kondisi Dirichlet Deret Fourier konvergen bila memenuhi syarat/ kondisi Dirichlet Teorema: Jika 1. f(x) terdefinisi dan bernilai tunggal, kecuali pada beberapa titik yang banyaknya berhingga pada interval ( -L, L) 2. f(x) periodik dengan periode 2 L 3. f(x) dan f (x) merupakan fungsi-fungsi yang kontinu pada setiap segmen pada interval (-L, L).

maka deret Fourier (1) dengan koefisien (2) dan (3) atau (4) dan (5) konvergen ke : 1. f(x) jika x merupakan titik kontinu pada interval (-L, L) 2. jika x adalah titik diskontinu

Contoh: Dari soal sebelumnya : bagaimanakah f(x) harus ditentukan pada x=-5; x=0 dan x=5 agar deret Fourier tersebut konvergen ke f(x) pada interval (-5, 5)

Jawab : Berhubung pada titik-titik continue, deret adalah konvergen ke f(x) maka pada titik-titik diskontinu agar deret konvergen, haruslah diambil konvergen ke : Bila kita definisikan f(x) sebagai, 3/2 , x = -5 0 , -5 < x < 0 f(x) = 3/2 , x = 0 3 , 0 < x < 5 3/2 , x = 5 Maka deret konvergen ke f(x) untuk -5 ≤ x ≤ 5

Fungsi Genap dan Fungsi Ganjil Fungsi f(x) disebut fungsi genap jika f(-x) = f(x) untuk setiap x. Contoh : f(x) = cos x f(x) = x 4 Fungsi polinomial dalam x yang suku- sukunya berpangkat genap merupakan fungsi genap. Jika f(x) fungsi genap maka :

Deret fourier dari fungsi genap: Jadi jika f(x) fungsi genap maka bn=0 sehingga yang muncul hanya suku yang mengandung cosinus (suku dari an)

Fungsi f(x) disebut fungsi ganjil jika : f(-x) = - f(x) untuk setiap x. Contoh : f(x) = sin x f(x) = x 3 Fungsi polinomial dalam x yang sukunya berpangkat ganjil merupakan fungsi ganjil. Jika f(x) fungsi ganjil maka :

Deret fourier dari fungsi ganjil: Jadi, jika f(x) fungsi ganjil maka an = 0, sehingga yang muncul hanya suku yang mengandung sinus (suku dari bn)

Deret Fourier Sinus atau Cosinus Separuh Jangkauan • Deret sinus dan cosinus setengah jangkauan adalah suatu deret fourier yang hanya mengandung suku sinus dan cosinus saja. • Apabila diinginkan deret setengah jangkauan yang sesuai dengan fungsi yang diberikan, fungsi yang dimaksud biasanya hanya diberikan dalam setengah interval dari (-L, L) yaitu pada interval (0, L). Setengah lainnya yaitu (-L, 0) ditentukan berdasarkan penjelasan fungsinya genap atau ganjil.

• Deret sinus setengah jangkauan adalah deret Fourier dengan: a. f(x) fungsi ganjil b. • Deret cosinus setengah jangkauan adalah deret Fourier dengan: a. f(x) fungsi genap b.

Contoh : Ekspansikan f(x) = x; 0<x<2 ke dalam; a. Deret sinus setengah jangkauan b. Deret cosinus setengah jangkauan

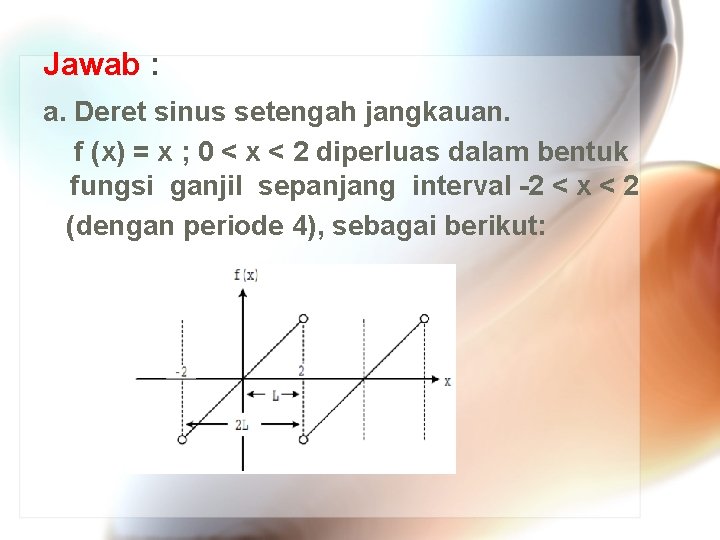
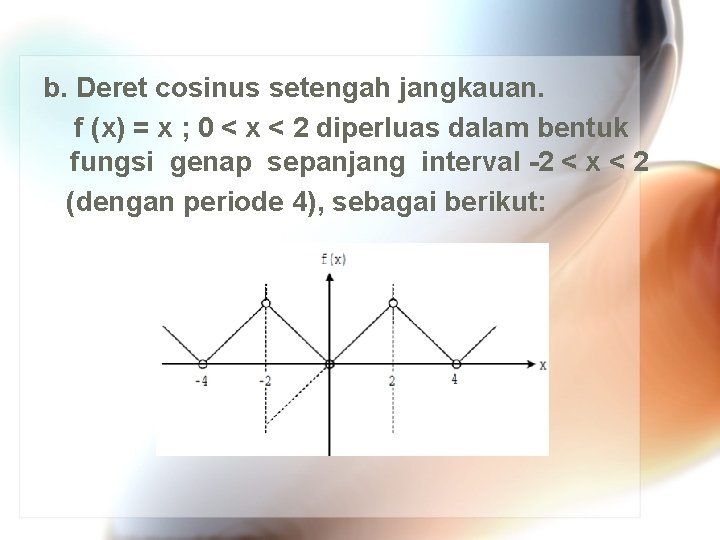
Jawab : a. Deret sinus setengah jangkauan. f (x) = x ; 0 < x < 2 diperluas dalam bentuk fungsi ganjil sepanjang interval -2 < x < 2 (dengan periode 4), sebagai berikut:

Sehingga an = 0 Jadi deret sinus setengah jangkauannya :

b. Deret cosinus setengah jangkauan. f (x) = x ; 0 < x < 2 diperluas dalam bentuk fungsi genap sepanjang interval -2 < x < 2 (dengan periode 4), sebagai berikut:

Sehingga bn = 0 Jadi deret cosinus setengah jangkauannya :

 Tentukan deret fourier dari fungsi berikut
Tentukan deret fourier dari fungsi berikut Contoh soal deret fourier fungsi genap dan ganjil
Contoh soal deret fourier fungsi genap dan ganjil Penerapan konsep barisan dan deret
Penerapan konsep barisan dan deret Harmonisa
Harmonisa Frequency of a cos function
Frequency of a cos function Fungsi periodik
Fungsi periodik Deret laurent
Deret laurent Turunan fungsi komposisi
Turunan fungsi komposisi Contoh soal fungsi non linear hiperbola
Contoh soal fungsi non linear hiperbola Invers transformasi fourier
Invers transformasi fourier Mengapa susunan unsur unsur diberi sisipan kata periodik
Mengapa susunan unsur unsur diberi sisipan kata periodik Sinyal periodik
Sinyal periodik Sifat reduktor dalam satu periode
Sifat reduktor dalam satu periode Ppt perkembangan sistem periodik unsur
Ppt perkembangan sistem periodik unsur Contoh retur pembelian
Contoh retur pembelian Sistem keperiodikan unsur
Sistem keperiodikan unsur Zirkadiane periodik
Zirkadiane periodik Contoh soal sinyal periodik dan aperiodik
Contoh soal sinyal periodik dan aperiodik Biaya periodik (period cost)
Biaya periodik (period cost) Bronzi element kimik
Bronzi element kimik Sebutkan dasar penyusunan tabel periodik mendeleev
Sebutkan dasar penyusunan tabel periodik mendeleev Contoh soal sinyal periodik dan aperiodik
Contoh soal sinyal periodik dan aperiodik Periode tabel periodik
Periode tabel periodik Jelaskan sistem periodik menurut oktaf new zealand
Jelaskan sistem periodik menurut oktaf new zealand Tabel periodik
Tabel periodik Kosto e mallit te shitur formula
Kosto e mallit te shitur formula Contoh soal persediaan metode periodik
Contoh soal persediaan metode periodik Garis dikatakan berimpit jika
Garis dikatakan berimpit jika Transistor cutoff
Transistor cutoff Dua buah finite states dikatakan ekuivalen jika
Dua buah finite states dikatakan ekuivalen jika Benda dikatakan bergerak lurus sebab
Benda dikatakan bergerak lurus sebab Testing dikatakan baik, jika
Testing dikatakan baik, jika Benda dikatakan bergerak apabila
Benda dikatakan bergerak apabila Sebuah benda dikatakan melakukan usaha apabila.
Sebuah benda dikatakan melakukan usaha apabila.