INTEGRASI DAN DIFERENSIASI NUMERIK 1 2 APROKSIMASI DERIVATIF

INTEGRASI DAN DIFERENSIASI NUMERIK 1. 2. APROKSIMASI DERIVATIF APROKSIMASI INTEGRAL

STRATEGI APROKSIMASI 1. 2. 3. Fungsi f diaproksimasi oleh polinomial interpolasi P. Derivatif polinomial P diambil sbg aproksimasi derivatif fungsi f. Integral polinomial P diambil sbg aproksimasi integral fungsi f. BAGAIMANA KESALAHAN APROKSIMASINYA ? Menentukan nilai aproksimasi lebih mudah daripada memperkirakan resiko kesalahan yang mungkin terjadi akibat aproksimasi tersebut.

Kesalahan aproksimasi dengan interpolasi Misalkan titik-titik berlainan di dalam dan Jika P adalah polinomial interpolasi maka setiap x terdapat ξ(x) ∈ (a, b) sehingga berlaku: approksimasi kesalahannya CONTOH: Misalkan fungsi f(x) = ex diaproksimasi oleh polinomial interpolasi didalam interval [0, 1]. Berikan estimasi kesalahan aproksimasinya. PENYELESAIAN : Misalkan titik interpolasi dan asumsikan berjarak sama, yaitu h. Jadi xj+1 - xj = h untuk setiap j. x 0 0 xj xj+1 h xn 1

Ambil sebarang x didalam [0, 1], kita akan menyelidiki kesalahan mutlak | f(x) - P(x) |. Pastilah ada indeks j sehingga xj ≤ xj+1. Berdasarkan teorema di atas, terdapatlah ξ(x) di dalam (0, 1) dan berlaku: Karena maka diperoleh: dan Diperhatikan fungsi mencapai ekstrim di tengah interval [xj, xj+1], yaitu di xm = (j+0. 5)h. Jadi maksimumnya Akhirnya diperoleh:

Bila diinginkan kesalahan aproksimasi tidak melebihi 10 -6 maka haruslah yang mengharuskan. Karena banyaknya sub interval n = (1 -0)/h harus bulat maka diambil h = 0. 001.

APROKSIMASI DERIVATIF n Derivatif f di titik x 0 adalah: y = f(x) f(x 0+h) – f(x 0) h x 0 Sederhananya, aproksimasi derivatif f’(x 0) adalah dengan mengambil h cukup kecil. x 0+h Untuk mengetahui kesalahan aproksimasinya, diperhatikan dua titik x 0 dan x 0+h, dibentuk polinomial interpolasi derajat satu yang melalui kedua titik ini, diperoleh: dimana R = . Selanjutnya, diambil derivatifnya dan didapat

Untuk x = x 0 maka diperoleh: diambil: . Akhirnya, dengan kesalahan (error): Untuk h>0, formula ini disebut aproksimasi selisih maju (forward-difference). Untuk h<0, diperoleh aproksimasi selisih mundur (backward-difference). dengan kesalahan (error):

n CONTOH : Tentukan aproksimasi derivatif fungsi f(x) = ln x di x 0=1. 8. Gunakan formula selisih maju dengan h = 0. 1, 0. 01 dan 0. 001 dan berikan analisis kesalahannya. n PENYELESAIAN : formula selisih maju diberikan oleh dengan error dimana n Diperoleh tabel: n Bandingkan dengan error sesungguhnya dimana derivatif eksaknya f’(1. 8) = 0. 55555. . .

FORMULA SELISIH TERPUSAT dimana adalah terletak diantara dan Jadi aproksimasinya dengan error E = • Diperhatikan jika h diperkecil, maka suku h 2 lebih cepat menuju nol dari pada suku h. Error aproksimasi yang memuat suku hp disebut mempunyai order aproksimasi p, dan ditulis dengan O(hp). • Formula selisih terpusat ini disebut juga formula tiga titik, karena melibat kan tiga titik x 0 -h, x 0 dan x 0+h. Formula tiga titik lainnya melibatkan titik x 0, x 0+h, x 0+2 h, yaitu dimana ξ 0 diantara x 0 dan x 0+2 h.

FORMULA LIMA TITIK 1. dimana ξ diantara x 0 -2 h dan x 0+2 h. 2. dimana ξ diantara x 0 dan x 0+4 h.

Order kesalahan aproksimasi : 1. Formula 2 titik (selisih maju, selisih mundur) mempunyai order 1. 2. Formula 3 titik mempunyai order 2. 3. Formula 5 titik mempunyai order 4. 4. Semakin tinggi order aproksimasi semakin akurat aproksimasi yang dihasilkan. CONTOH : Beberapa nilai dari f(x) = x ex diberikan pada tabel berikut. Karena f’(x) = (x+1)ex maka nilai eksak derivatif f di x=0. 2 adalah f’(2. 0) = 22. 167168. Gunakan berbagai macam formula untuk menghitung aproksimasi derivatifnya. Banding errornya dan formula mana yang paling akurat. PENYELESAIAN: Gunakan h = 0. 1, terapkan dua formula 2 titik (selisih maju dan selisih mundur), dua formula 3 titik dan dua formula 5 titik.

APROKSIMASI DERIVATIF KEDUA n Fungsi f diekspansi dalam deret Taylor disekitar x 0, kemudian dievaluasi di titik x 0+h dan x 0 -h diperoleh: dan dimana diperoleh: n Kedua bentuk ini dijumlahkan, Berdasarkan teorema nilai antara, terdapat ξ diantara ξ 0 dan ξ-1 sehingga

Aproksimasi derivatif kedua (Lanjutan) n Diperoleh: ≈ f’’(x 0) n n Error CONTOH: Kembali perhatikan fungsi f(x) = xex. Fungsi ini mempunyai derivatif kedua f’’(x) = (x+2)ex. Untuk x 0=2. 0 diperoleh derivatif eksak adalah f’’(2. 0) = 29. 556224. Hitunglah aproksimasi derivatif kedua dengan menggunakan h=0. 1 dan h=0. 2. PENYELESIAN : q h = 0. 1 q h = 0. 2 q Error masing-masing adalah .

APROKSIMASI INTEGRAL n FORMULA QUADRATURE SEDERHANA n n n METODA TITIK TENGAH METODA TRAPESIUM METODA SIMPSON n FORMULA QUADRATURE BERSUSUN n INTEGRASI GAUSS.

FORMULA SEDERHANA n Diperhatikan integral jumlahan yaitu . Formula qudrature berbentuk digunakan sebagai aproksimasi untuk integral, ≈ xi disebut koordinat dan ai disebut bobot. n Seperti pada aproksimasi, fungsi f terlebih dahulu diaproksimasi oleh polinomial interpolasi, kemudian integral dari polinomial ini diambil sebagai aproksimasi integral fungsi f.

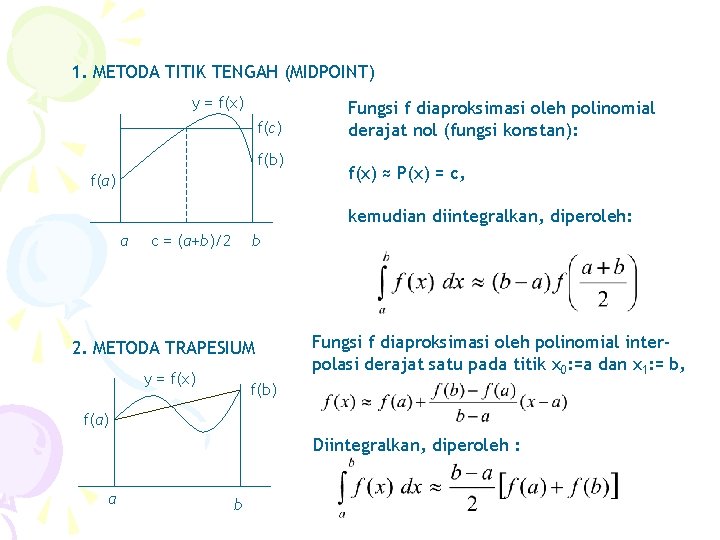
1. METODA TITIK TENGAH (MIDPOINT) y = f(x) f(c) f(b) f(a) Fungsi f diaproksimasi oleh polinomial derajat nol (fungsi konstan): f(x) ≈ P(x) = c, kemudian diintegralkan, diperoleh: a c = (a+b)/2 b 2. METODA TRAPESIUM y = f(x) Fungsi f diaproksimasi oleh polinomial interpolasi derajat satu pada titik x 0: =a dan x 1: = b, f(b) f(a) Diintegralkan, diperoleh : a b

3. METODA SIMPSON y = P(x) y = f(x) f(b) f(a) a Fungsi f diaproksimasi oleh polinomial interpolasi derajat dua di titik-titik x 0= a, x 1= c: = (a+b)/2 dan x 3 = b, yaitu c b Diperoleh CONTOH : Terapakan metoda midpoint, trapesium dan Simpson untuk menghitung integral : dimana f adalah beberapa fungsi dasar Metoda manakah yang paling akurat?

PENYELESAIAN: untuk f(x) = x 2, eksaknya adalah 1. Midpoint M = (2 -0)f(1) = 2. 000, 2. Trapesium T = (2 -0)/2 [f(0)+f(2)] = 4. 000, 3. Simpson S = (1/3)[f(0) + 4 f(1) + f(2)] = 2. 667. Untuk SOAL lainnya diselesaikan sendiri ! ESTIMASI ERRORNYA ? = 2. 667.

ERROR FORMULA QUADRATURE 1. METODA MIDPOINT h x 0 h x 1 x 2 2. METODA TRAPESIUM h x 0 x 1 3. METODA SIMPSON h x 0 h x 1 x 2

Pada metoda midpoint dan trapesium, suku errornya memuat derivatif kedua. Bila fungsi yang diintegralkan adalah polinomial berderajat paling tinggi 1 maka kedua metoda ini memberikan hasil eksak krn derivatif keduanya nol. CONTOH: Gunakan kedua metoda ini untuk mengaproksimasi integral f(x) = 2 x+1, dari x=0 sampai x=2. Bandingkan hasilnya dengan eksaknya? Pada metoda Simpson, suku errornya memuat derivatif keempat. Bila fungsi yang diintegralkan adalah polinomial berderajat paling tinggi 3 maka kedua metoda ini metoda Simpson memberikan hasil eksak krn derivatif keempatnya nol. CONTOH: Gunakan metoda Simpson untuk mengintegralkan fungsi f(x) = x 3+2 x 2 -3 x+1 dari x=0 sampai x=2. Bandingkan hasilnya dengan eksaknya? CONTOH : Diberikan masalah menghitung nilai integral: a) Tentukan nilai aproksimasi dengan menggunakan ketiga metoda di atas. b) berikan estimasi error untuk tiap-tiap metoda c) hitung error sesungguhnya

PENYELESAIAN : f(x) = ex/2, f’’(x) = (1/4) ex/2, f(4)(x) = (1/16) ex/2. a) Midpoint: di sini x 0 = 0, x 1 = 1, x 2 = 2 dan h = 1 M = 2 h f(x 1) = 2 e 1/2 = 3. 2974 b) Trapesium: di sini x 0 = 0, x 1 = 2 dan h = 2 T = (2/2)[e 0 + e 1] = 3. 7183 c) Simpson: di sini x 0 = 0, x 1 = 1, x 2 = 2 dan h = 1 S = (1/3)[e 0+4 e 1/2+e 1] =3. 4377 b) Error pada Midpoint EM = (h 3/3)f”’( � ) = (1/3) (1/4) e�/2 < (1/12) e 1 = 0. 2265, sebab c) �terletak diantara 0 dan 2. d) Error pada Trapesium ET = (h 3/3)f”’( � ) = (1/3) (1/4) e�/2 < (1/12) e 1/2 = 0. 1374. sebab e) �terletak diantara 0 dan 1. f) Error pada Simpson ES = (h 5/90) f(4)(� ) = (1/90) (1/16) e�/2 < (1/90) (1/16) e 1 = 0. 0019. g) c) Nilai integral sesungguhnya adalah h) i) j) k) Error sesungguhnya untuk: metoda midpoint adalah | 3. 2974 – 3. 4366 | = 0. 1392 metoda trapesium adalah | 3. 7183 – 3. 4366| = 0. 2817 metoda Simpson adalah | 3. 4377 – 3. 4366| = 0. 0011. l) Metoda Simpson memberikan hasil paling akurat. Error sesungguhnya tidak akan m) melebihi error estimasi.

FORMULA QUADRATURE BERSUSUN n ILUSTARASI: Metoda Simpson dalam menghitung integral: n n Nilai eksaknya adalah: 53. 59815. Formula diterapkan langsung pada [0, 4], yaitu x 0=0, x 1= 2 dan x 2=4, h=2. Diperoleh: Errornya = 3. 17143. n Interval [0, 4] dipecah menjadi [0, 2] dan [2, 4]. Formula diterapkan pada kedua interval ini, yaitu x 0=0, x 1= 1 dan x 2=2, h=1 pada [0, 2], dan x 0=2, x 1= 3 dan x 2=4, h=1 pada [0, 4]. Diperoleh: Errornya = 0. 56270.

¢ Interval [0, 4] dipecah menjadi 4 subinterval dan [3, 4]. Diperoleh: [0, 1], [1, 2], [2, 3] Errornya = 0. 01807 ¢ Semakin kecil subinterval dimana formula Simpson diterapkan semakin teliti nilai aproksimasi.

Interval [a, b] dipecah menjadi sejumlah subinterval h a=x 0 x 1 x 2 xk-1 xk xk+1 xn=b Agar metoda Simpson dapat diterapkan pada semua subinterval maka dipilih n genap. Diperoleh: dimana. Bila disederhanakan maka diperoleh formula quadrature Simpson bersusun (composite) : dimana dan .

Dengan ide yang sama diperoleh formula quadrature trapesium bersusun: dimana dan . Di sini n tidak harus genap. Untuk formula midpoint bersusun, perlu diambil n genap dan diperoleh: dimana dan

CONTOH: Aproksimasilah dengan menggunakan h = 0. 25 a) metoda trapesium bersusun b) metoda Simpson bersusun c) metoda midpoint bersusun PENYELESAIAN: Diketahui. Karena h = 0. 25 maka diperoleh titik partisi x 0= 0, x 1=0. 25, x 2=0. 5, x 3=0. 75, x 4=1. 00, x 5=1. 25, x 6=1. 50, x 7=1. 75, x 8=2. 00. a. Metoda trapesium b. Metoda Simpson c. Metoda midpoint Komputasinya diselesaikan sendiri. Bandingkan dengan hasil eksaknya. Apakah metoda Simpson tetap paling bagus. Bagaimana estimasi errornya.