Analisa Numerik Integrasi Numerik Review Ide Pemakaian Polinom

Analisa Numerik Integrasi Numerik

Review Ide Pemakaian Polinom Interpolasi • Review ide pemakaian polinom interpolasi dlm. menaksir turunan dan integrasi : 1. f(x) diketahui, tetapi sulit dioperasikan (turunkan, integrasi). 2. f(x) tdk. diketahui, tetapi harga f(x) pd. titik x 0, x 1, . . . , xk diketahui. • Jk. L adalah operator pengganti turunan atau integrasi, mk. penaksiran harga turunan atau integrasi secara umum berbentuk : • Proses penggantian L(f) dng. L(Pk) disebut diskritisasi, disebut kesalahan diskritisasi. 2

Review Ide Pemakaian Polinom Interpolasi • Masalah ketelitian, sulit dicapai karena : 1. Terbatasnya panjang word suatu komputer. 2. Hilangnya digit signifikan pada saat dua nilai yang hampir sama dikurangi. • Jd. ada h optimum, dimana utk. 3

Aturan Dasar [a, b] dibagi-bagi menjadi N interval (tidak perlu sama). a = x 0 < x 1 < x 2 <. . . <xn = b Misal : Pi, k(x) (i = 1, . . . , N) adalah polinom interpolasi utk. f(x) pd. interval (xi-1, xi). Catatan : Utk. kemudahan pembahasan, dimisalkan xi–xi-1 sama xi = a + ih, i = 0, . . . , N, h = (b-a)/N Notasi fs = f(a + sh), mk. fi = f(xi), i = 0, . . . , N 4

Aturan-Aturan Dasar di mana I(Pk) = A 0 f(x 0) + A 1 f(x 1) +. . . + Akf(xk) [jumlah berbobot Ai] xi, f(xi) i = 0, . . . , k diketahui : Ai dpt. dihitung dng. Ai = I(li), li = polinom Langrange ke-i. k = 0, x 0 = a Aturan Segi Empat f(x) 5

Aturan-Aturan Dasar – k = 0, x 0 = (a+b)/2 Aturan Titik Tengah f(x) – k = 1, x 0 = a, x 1 = b Aturan Trapesium f(x) – k = 2, x 0 = a, x 1 = (a+b)/2, x 2 = b Aturan Simpson f(x) 6

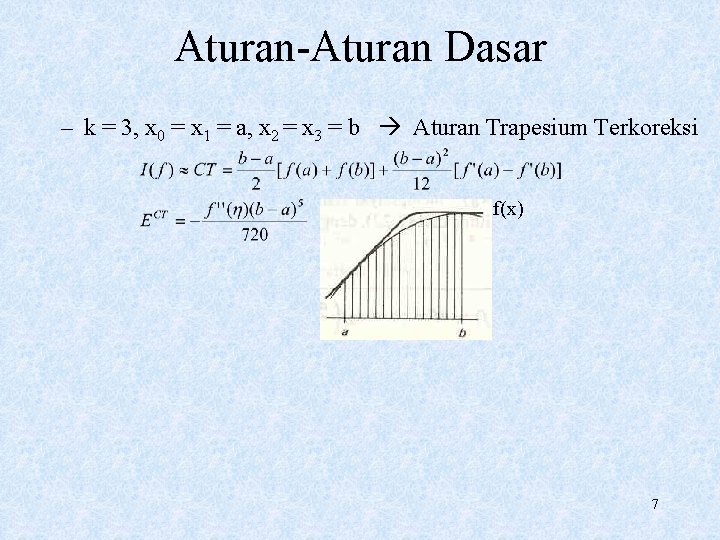
Aturan-Aturan Dasar – k = 3, x 0 = x 1 = a, x 2 = x 3 = b Aturan Trapesium Terkoreksi f(x) 7

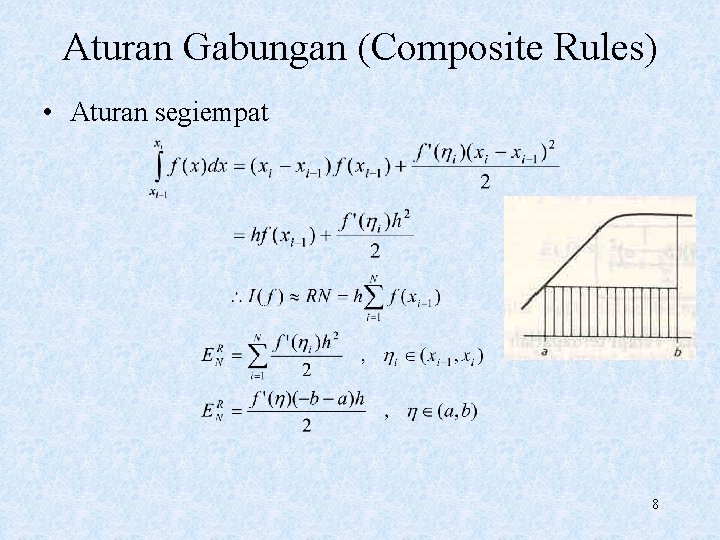
Aturan Gabungan (Composite Rules) • Aturan segiempat 8

Aturan Gabungan (Composite Rules) • Aturan Simpson f(x) 9

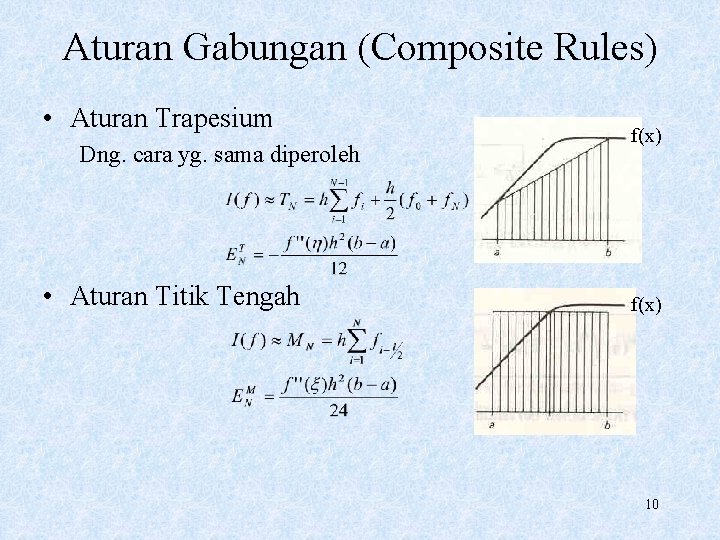
Aturan Gabungan (Composite Rules) • Aturan Trapesium Dng. cara yg. sama diperoleh • Aturan Titik Tengah f(x) 10

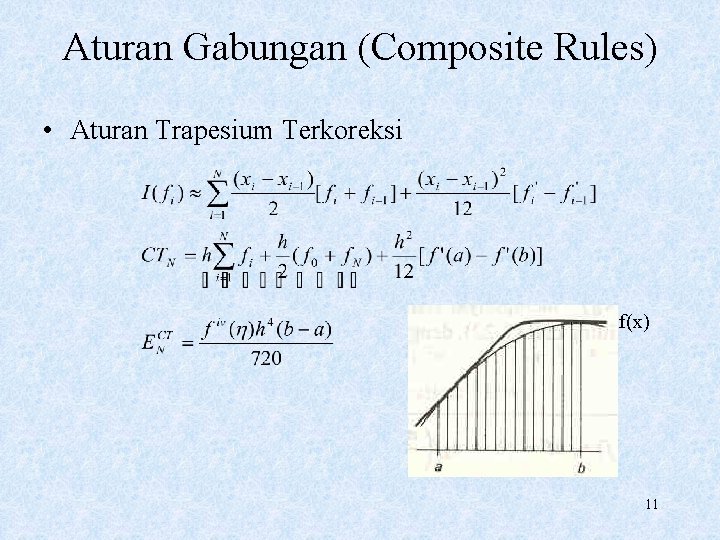
Aturan Gabungan (Composite Rules) • Aturan Trapesium Terkoreksi f(x) 11

Contoh • Dng. memakai aturan trapesium gabungan, tentukan N sehingga teliti sampai 6 digits Jwb. : Errornya adalah –f’’( )N-2/12 , ∈ (a, b) Batas errornya adalah : max |f’’(x)| pd. [0, 1] terjadi pada x = 0 atau x = 0, 1 12

Metoda Adaptif Quadrature • Adaptif lebar sub interval ditentukan oleh perilaku lokal integralnya (fungsinya). – Besar interval keseluruhan tidak harus sama. • Cocok utk. menghitung I(f) dlm. ketelitian tertentu dng. penghitungan fungsi lebih sedikit jika subinterval ditentukan dengan baik. • Perhatikan aturan trapesium gabungan di mana a = x 0 < x 1 <. . . < x. N = b tidak perlu berjarak sama. Besar error tergantung Jd. jika f’’(x) ‘kecil’, maka pakai interval ‘besar’. jika f’’(x) ‘besar’, maka pakai interval ‘kecil’. 13

Adaptive Quadrature Berdasarkan Aturan Simpson • Diberikan f(x) pada [a, b] dan bilangan kecil > 0. Cari p (aproksimasi) terhadap di mana |P – I| ≤ dng. memakai penghitungan fungsi sesedikit mungkin. • Misal : xi+1 – xi = h h – xi xi+1 xi + h/2 Dng. subinterval ini hitung Si pendekatan dari Ii Si = h/6 {f(xi) + 4 f(xi + h/2) + f(xi+1)} 14

Adaptive Quadrature Berdasarkan Aturan Simpson h – xi xi + h/4 Hitung xi + h/2 xi + 3 h/4 xi+1 pendekatan dari Ii – Dng. memakai Error Simpson diperoleh : 15

Adaptive Quadrature Berdasarkan Aturan Simpson • Jk. [a, b] ada N interval maka errornya memenuhi lalu : 16

Contoh • Contoh Dengan memakai adaptive quadrature yg. berdasarkan aturan Simpson, cari aproksimasi (pendekatan) thd. integral : dng. ketelitian kesalahan = 0. 0005 (harga sebenarnya I = 2/3). Jawab : [0, 1] [0, ½] dan [½, 1] pada [½, 1], h = ½ ok 17

Contoh pada [0, ½] [0, ¼] dan [¼, ½] 18