DERIVATIF A Pengertian Definisi Derivatif fungsi f ditulis




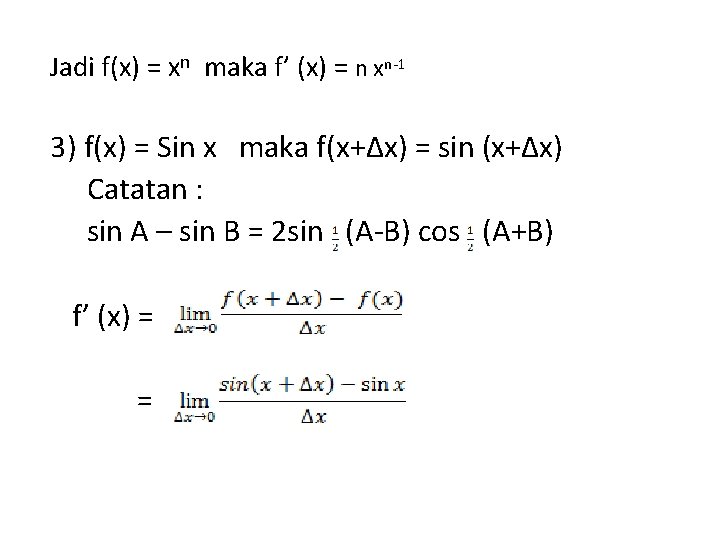





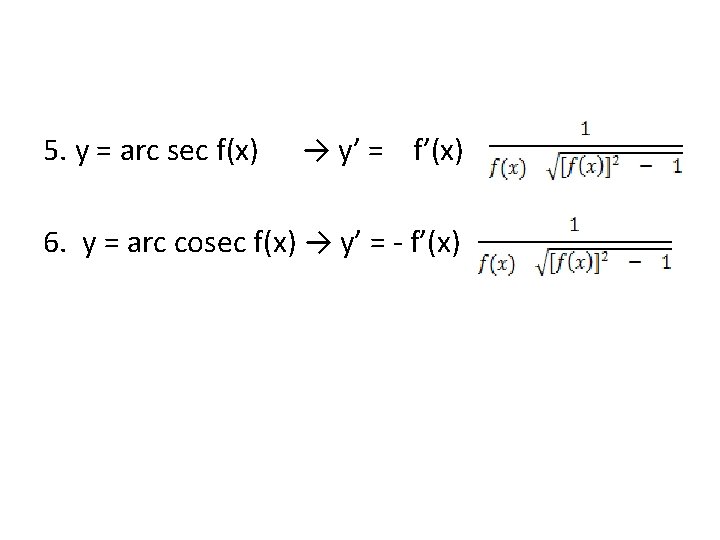



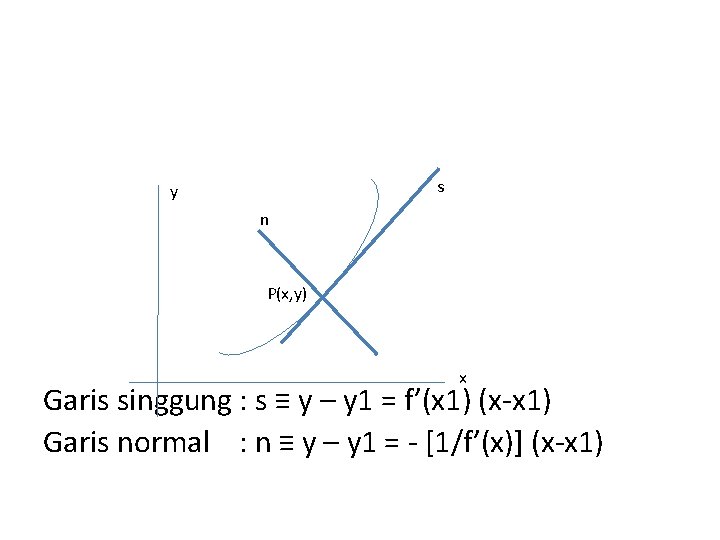

![Persamaan garis normal : n ≡ y – y 1 = - [1/f’(x)] (x-x Persamaan garis normal : n ≡ y – y 1 = - [1/f’(x)] (x-x](https://slidetodoc.com/presentation_image_h/0b43ab15ac86739297f12677ca0316b0/image-17.jpg)




- Slides: 21

DERIVATIF

A. Pengertian. Definisi : Derivatif fungsi f (ditulis f’ ) adalah fungsi dengan rumus : f’ (x) = Apabila limit ini ada untuk setiap x ϵ Df.

Contoh : Carilah f’(x) jika : 1) f(x) = C, C adalah bilangan konstan sembarang. 2) f(x) = x 2 3) f(x) = Sin x Penyelesaiain : 1) f(x) = C maka f(x+∆x) = C

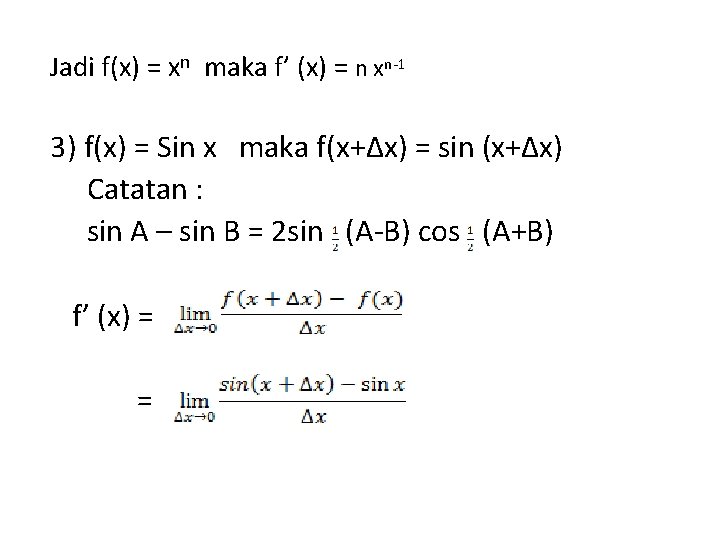
Jadi f(x) = xn maka f’ (x) = n xn-1 3) f(x) = Sin x maka f(x+∆x) = sin (x+∆x) Catatan : sin A – sin B = 2 sin (A-B) cos (A+B) f’ (x) = =


B. Derivatif Fungsi Aljabar. 1. f(x) = c → f’(x) = 0, dimana c = bil. Konstan atau : y = c → y’ = 0 2. y = xn → y’ = n xn-1 3. y = f(x) + g(x) → y’ = f’(x) + g’(x) 4. y = f(x). g(x) → y’ = f(x) g’(x) + f’(x) g(x) 5. y = → y’ = 6. Y= [f(x)]n → y’ = n [f(x)]n-1. f’(x)

Contoh : Tentukan derivatif dari fungsi berikut : 1) y = 5 → y’ = 0 2) y = x 5 ; maka y’ = 5 x 4 3) y = [ x 5 + 3 ] + [ x 2 + 5 ] → y’ = [5 x 4] + [2 x] 4) y = [ x 5 + 3 ]. [ x 2 + 5 ] → y’ = [ x 5 + 3 ]. [ 2 x ] + [ 5 x 4 ]. [ x 2 + 5 ] 5) y = → y’ = 6) y = [ x 5 + 3 ]7 = → y’ = 7 [ x 5 + 3 ]6. [ 5 x 4 ]

C. Derivatif Fungsi Trigonometri. 1. y = sin f(x) → y’ = f’(x) cos f(x) 2. y = cos f(x) → y’ = - f’(x) sin f(x) 3. y = tg f(x) → y’ = f’(x) 4. y = ctg f(x) → y’ = - f’(x) 5. y = sec f(x) → y’ = f’(x) sec f(x) tg f(x) 6. y = cosec f(x) → y’ = - f’(x) cosec f(x) ctg f(x)

D. Derivatif Fungsi Cyclometri. 1. y = arc sin f(x) → y’ = f’(x) 2. y = arc cos f(x) → y’ = - f’(x) 3. y = arc tg f(x) → y’ = f’(x) 4. y = arc ctg f(x) → y’ = - f’(x)
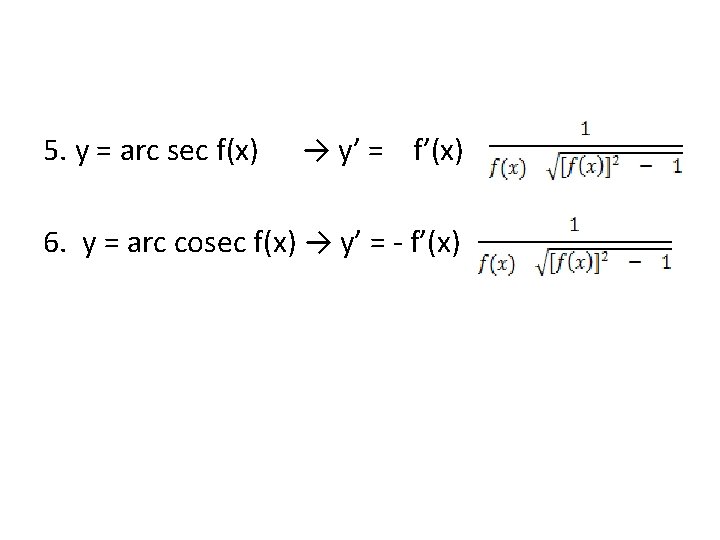
5. y = arc sec f(x) → y’ = f’(x) 6. y = arc cosec f(x) → y’ = - f’(x)

E. Derivatif Fungsi Logaritma dan Fungsi Eksponensial. 1. y = ln f(x) → y’ = f’(x) 2. y = → y’ = f’(x). 3. y = → y’ = f’(x). . ln a

F. Derivatif Fungsi Hiperbolicus. 1. y = sinh x → y’ = cosh x 2. y = cosh x → y’ = sinh x 3. y = tgh x → y’ = 4. y = ctgh x → y’ = - 5. y = sech x → y’ = - sech x. tgh x 6. y = cosech x → y’ = - cosech x. ctgh x

G. Garis Singgung dan Garis Normal. Misal diberikan suatu fungsi y=f(x) dengan titik P(x, y) pada kurva. Maka melalui titik P dapat dibuat garis singgung (≡ s) dan garis normal (≡ n). Dimana garis normal adalah garis yang tegak lurus garis singgung.
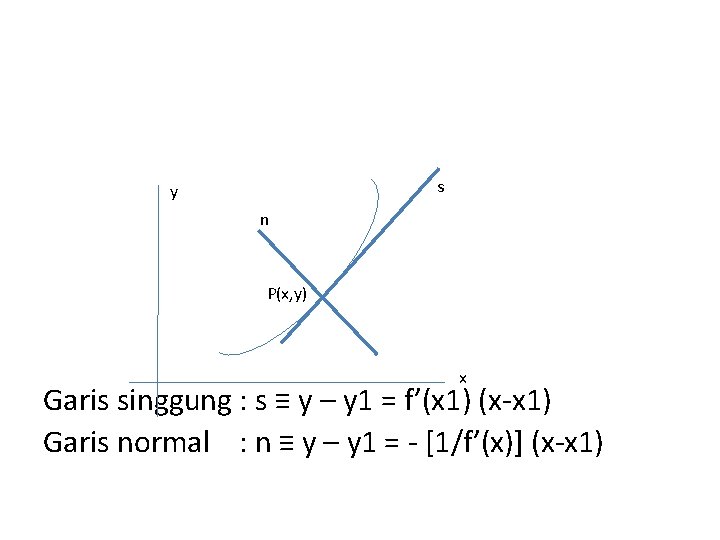
sx y n P(x, y) x xx Garis singgung : s ≡ y – y 1 = f’(x 1) (x-x 1) Garis normal : n ≡ y – y 1 = - [1/f’(x)] (x-x 1)

Contoh : Cari garis singgung dan garis normal pada kurva y = x 2 -4 x + 3 di titik P(4, 3) Penyelesaian : y = f(x) = x 2 -4 x + 3 → y’ = f’(x) = 2 x - 4 → f’(x 1=4) = 2(4) – 4 = 4 P(4, 3) x 1 = 4 ; y 1 = 3. Persamaan garis singgung : s ≡ y – y 1 = f’(x 1) (x-x 1) y – 3 = 4 (x-4) y = 4 x - 13
![Persamaan garis normal n y y 1 1fx xx Persamaan garis normal : n ≡ y – y 1 = - [1/f’(x)] (x-x](https://slidetodoc.com/presentation_image_h/0b43ab15ac86739297f12677ca0316b0/image-17.jpg)
Persamaan garis normal : n ≡ y – y 1 = - [1/f’(x)] (x-x 1) y – 3 = - [ ¼ ] (x-4) y = x + 4

H. Titik Stasioner Nilai Maksimum, Minimum, dan Titik Stasioner. 1) f(x 0 ) = nilai maksimum jika f pada domain S berlaku f(x 0 ) > f(x) untuk setiap x anggota dari S. 2) f(x 0 ) = nilai minimum jika f pada domain S berlaku f(x 0 ) < f(x) untuk setiap x anggota dari S. 3) Misal f(x) = 1/x dan S = [1, 3], maka f(1) = 1 adalah nilai maksimum dan f(3) = 1/3 adalah nilai minimum.

4) Titik Stasioner diperoleh dari f’(x) = 0. Merupakan titik yang akan memberikan f bernilai maksimum atau minimum. 5) Misal f(x) = x 2 dan S = [ -1, 3]. Maka titik di ujung interval adalah -1 dan 3, sehingga nilai f yaitu f( -1) = 1 dan f(3) = 9, belum bisa digunakan untuk menentukan nilai maksimum dan minimum dari fungsi f.

6) Turunan dari f(x) adalah f’(x) = 2 x = 0, jadi x = 0, maka f(0) = 0 Sehingga f(x) = x 2 , nilai maksimumnya adalah 9 dan nilai minimumnya = 0. 7) Sebuah kapal terhenti di tengah laut di A, berjarak 2 mil ke pantai B, jika yang akan dituju untuk mencari bantuan adalah di C yang berjarak 6 mil dari B. Berapa waktu tercepat dari A ke C, jika, berlari di darat kecepatannya 10 mil/jam dan naik sekoci kecepatannya 6 mil/jam.

8) Kertas karton berbentuk bujur sangkar dengan sisi-sisinya berukuran 15 cm. Jika setiap ujung dipotong berbentuk bujur sangkar. Berapa ukuran kotak terbuka dengan volume terbesar yang dapat dibuat dari karton tsb.
 Definisi derivatif
Definisi derivatif Perbedaan fungsi linear dan non linear
Perbedaan fungsi linear dan non linear Contoh soal fungsi transenden
Contoh soal fungsi transenden Kalkulus turunan fungsi
Kalkulus turunan fungsi Diferensial
Diferensial Film
Film Contoh instrumen derivatif
Contoh instrumen derivatif Pengertian instrumen derivatif
Pengertian instrumen derivatif Etiket biru
Etiket biru Karangan 3 perenggan
Karangan 3 perenggan Hal yang tidak perlu dicatat dalam notula rapat adalah
Hal yang tidak perlu dicatat dalam notula rapat adalah Kata depan adalah
Kata depan adalah Panolong
Panolong Popular opinions
Popular opinions Penyataan bahasa mesin
Penyataan bahasa mesin Pembagian perjanjian lama
Pembagian perjanjian lama Perkalian linear
Perkalian linear Naskah berita tv
Naskah berita tv Jika p½ ditulis dalam bentuk akar menjadi
Jika p½ ditulis dalam bentuk akar menjadi Surat tujuan
Surat tujuan Sistem kode
Sistem kode Definisi matriks
Definisi matriks