MATRIKS A PENGERTIAN NOTASI DAN ORDO MATRIKS 1

MATRIKS

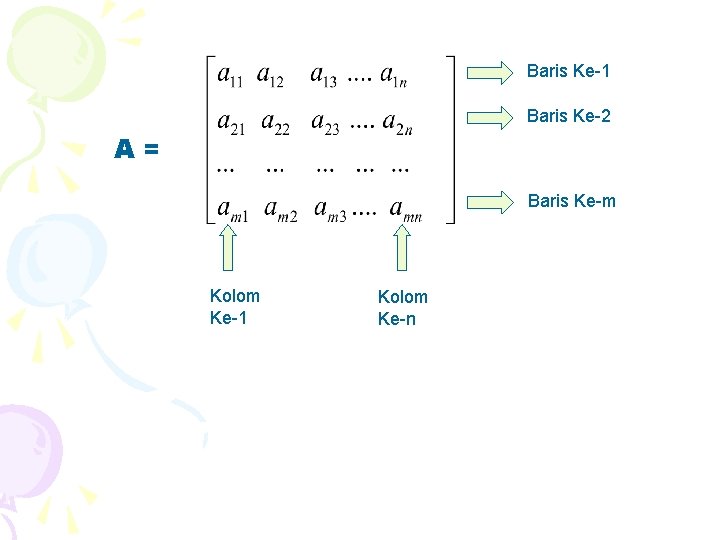
A. PENGERTIAN, NOTASI DAN ORDO MATRIKS 1. Pengertian Matriks adalah suatu susunan bilangan yang diatur dalam baris dan kolom berbentuk persegi panjang. Susunan ini diletakkan dalam ( ), atau [ ] atau || ||

Baris Ke-1 Baris Ke-2 A= Baris Ke-m Kolom Ke-1 Kolom Ke-n

CONTOH 1 : A = Tentukan: a. banyak baris matriks A b. banyak kolom matriks A c. a 11, a 24, a 32

2. Notasi Matriks Suatu matriks diberi notasi dengan huruf kapital, seperti A, B, C dan sebagainya. Contoh : A =

3. Ordo Matriks Ordo (ukuran) dari matriks adalah banyak baris dan kolom yang dimiliki matriks yang bersangkutan. n A m x n berarti matriks A berordo m x n artinya matriks A memiliki m buah baris dan n buah kolom n CONTOH: A= Matriks A berordo 3 x 4

4. Tranpose Matriks n n Matriks berordo n x m yang didapat dari penukaran baris dengan kolom matriks Am xn disebut tranpose dari A dan dinyatakan dengan notasi At (A tranpose) Contoh : Tentukan tranpose dari matriks A=

B. KESAMAAN DUA MATRIKS a. b. Dua buah matriks A dan B dikatakan sama, jika : Ordonya sama Nilai tiap elemen yang seletak (bersesuaian) sama

Contoh : Carilah nilai x, y dan z dari : =

adalah matriks yang hanya terdiri dari satu baris.

adalah matriks yang hanya terdiri dari satu kolom.

adalah matriks yang jumlah baris dan kolomnya sama. Matriks persegi berordo nxn

C. PENJUMLAHAN DAN PENGURANGAN MATRIKS 1. Penjumlahan Matriks Dua buah matriks A dan B dapat dijumlahkan jika keduanya memiliki ordo yang sama. Hasil operasi penjumlahan adalah matriks baru yang ordonya sama dengan matriks semula yang elemennya diperoleh dengan menjumlahkan elemen-elemen seletak pada matriks A dan B.

CONTOH : • Diberikan tiga buah matriks berikut : • Tentukan A + B dan A + C

2. Pengurangan Matriks Jika A dan B adalah dua matriks yang ordonya sama, maka A – B = A+ (-B) CONTOH : Diberikan matriks berikut ini Tentukan A – B dan A - C

3. Perkalian Matriks dengan Bilangan Skalar n Diberikan matriks n Tentukan 2 A, -3 A dan ½ A

Sifat-sifat Perkalian Bilangan Real dengan Matriks Untuk bilangan real k 1 dan k 2 dan untuk matriks A dan B yang berordo sama, berlaku : o (k 1 k 2) A = k 1 (k 2 A) o K 1 (A + B ) = k 1 A + k 1 B = (A + B) k 1 o (k 1 + k 2) A = k 1 A + k 2 A o 1. A = A o 0. A = 0

4. Perkalian Matriks n n Perkalian dua matriks A x B ada hasilnya bila banyaknya kolom matriks A (kiri) sama dengan banyaknya baris matriks B (kanan) Matriks hasilnya mempunyai baris sebanyak baris matriks kiri dan mempunyai kolom sebanyak kolom matriks kanan.

CONTOH :

CONTOH :

CONTOH :

Lihatlah matriks A dan matriks B berikut ini : Apakah perkalian AB = BA ? Ternyata perkalian AB ≠ BA, hal ini menunjukkan bahwa pada perkalian dua matriks tidak berlaku sifat komutatif

Matriks Satuan Adalah matriks persegi-n dengan semua elemen diagonal utamanya 1 dan elemen lainnya nol (dilambangkan dengan I) n Untuk matriks persegi ordo 2 matriks identitasnya adalah n

Misalkan matriks

INVERS MATRIKS n Determinan Matriks Ordo 2 x 2 determinan dari matriks A ditulis det. A atau | A |, didefinisikan :

Contoh :

n Invers Matriks Ordo 2 x 2 Jika A dan B adalah matriks-matriks persegi yang ordonya sama dan AB = BA = I Maka B adalah invers dari A, ditulis B = A-1 dan A adalah invers dari B, ditulis A = B-1

Contoh : n Tentukan invers matriks

Matriks Singular dan Matriks Non Singular n Suatu matriks dikatakan singular jika determinannya nol dan non singular jika determinannya tidak nol.

Contoh : n Diberikan matriks-matriks : Manakah dari matriks-matriks itu yang merupakan matriks singular atau nonsingular ?

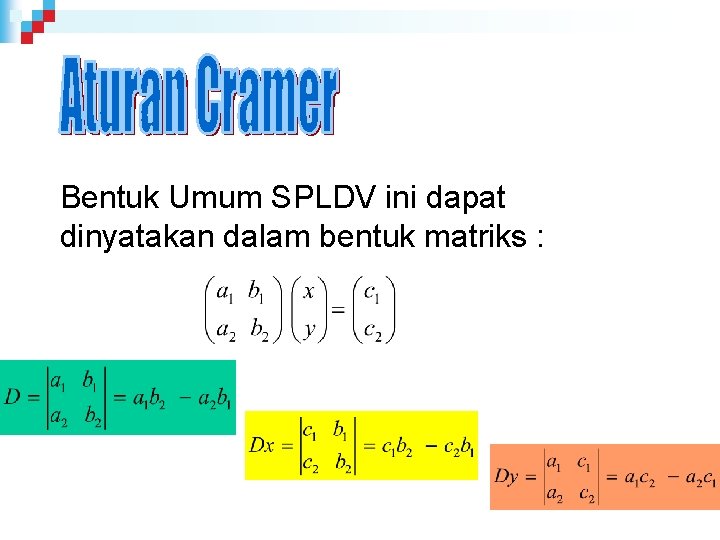
Bentuk Umum SPLDV : a 1 x + b 1 y a 2 x + b 2 y = c 1 = c 2 Bentuk Umum SPLDV ini dapat dinyatakan dalam bentuk matriks :

Misalkan : Maka persamaan matriks di atas dapat ditulis sebagai AX = B Sehingga SPLDV tersebut dapat diselesaikan dengan menggunakan persamaan matriks dalam bentuk: A X = B → X = A -1 B

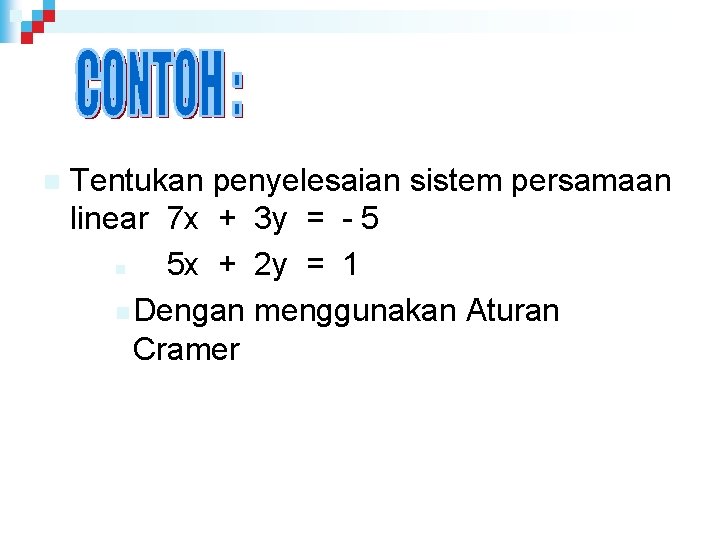
n Tentukan penyelesaian sistem persamaan linear 7 x + 3 y = - 5 n 5 x + 2 y = 1 n Dengan menggunakan matriks

Bentuk Umum SPLDV ini dapat dinyatakan dalam bentuk matriks :

Dari hasil di atas maka :

n Tentukan penyelesaian sistem persamaan linear 7 x + 3 y = - 5 n 5 x + 2 y = 1 n Dengan menggunakan Aturan Cramer

1. Tentukan penyelesaian SPLDV berikut dengan menggunakan persamaan matriks : n a. 2 x + 3 y = 12 n 3 x + 5 y = 19 n b. 2 x - 4 y – 4 = 0 n 4 x - 6 y – 7 = 0 n c. 5 x – 4 y - 3 = 0 n -2 x + 3 y + 1 = 0 n

2. Tentukan penyelesaian SPLDV berikut dengan menggunakan aturan Cramer : a. x + y = - 1 2 x - y = 7 b. 2 x + y = 5 3 x - 2 y = 4 c. -7 x + 4 y = -2 5 x + 3 y = 19

Invers Matriks berordo 3 x 3 n Jika A adalah matriks non singular, maka invers dari A adalah :

1. Minor n Jika elemen-elemen pada baris ke-i dan kolom ke-j dari matriks A berordo 3 x 3 dihapuskan, maka didapat matriks baru berordo 2 x 2, dengan determinannya disebut minor dari determinan matriks A dan dinyatakan dengan |Mij|

Misalkan matriks A berordo 3 x 3 adalah : Minor |M 11| adalah : Jika baris ke-1 dan kolom ke-1 dihapuskan, maka didapat

Minor |M 12| adalah : Jika baris ke-1 dan kolom ke-2 dihapuskan, maka didapat

Minor |M 13| adalah : Jika baris ke-1 dan kolom ke-3 dihapuskan, maka didapat

2. Kofaktor n Kofaktor dari baris ke-i dan kolom ke-j dinyatakan dengan Aij yang ditentukan dengan rumus : Aij = (-1) i + j |Mij|

Kofaktor-kofaktor dari matriks A adalah : n n n n n A 11 = (-1) 1 + 1 |M 11| = |M 11| A 12 = (-1) 1 + 2 |M 12| = -|M 12| A 13 = (-1) 1 + 3 |M 13| = |M 13| A 21 = (-1) 2 + 1 |M 21| = -|M 21| A 22 = (-1) 2 + 2 |M 22| = |M 22| A 23 = (-1) 2 + 3 |M 23| = -|M 23| A 31 = (-1) 3 + 1 |M 31| = |M 31| A 32 = (-1) 3 + 2 |M 32| = -|M 32| A 33 = (-1) 3 + 3 |M 33| = |M 33|

3. Adjoint n Jika matriks A berordo 3 x 3, maka :

4. Determinan matriks Berordo 3 x 3 n Nilai determinan dari matriks A ditulis |A| atau det A dapat ditentukan dengan rumus : n |A| = a 11 A 11 + a 12 A 12 + a 13 A 13 = a 11|M 11| - a 12|M 12| + a 13|M 13|

n |A| = a 21 A 21 + a 22 A 22 + a 23 A 23 = -a 21|M 21| + a 22|M 22| - a 23|M 23| n |A| = a 31 A 31 + a 32 A 32 + a 33 A 33 = a 31|M 31| - a 32|M 32| + a 33|M 33|

Kaidah Sarrus a 11 a 12 a 21 a 22 a 31 a 32 = a 11 a 22 a 33+ a 12 a 23 a 31+a 13 a 21 a 32 – a 31 a 22 a 13 – a 32 a 23 a 11 - a 33 a 21 a 12

Tentukan invers matriks berikut :