Great Theoretical Ideas In Computer Science Steven Rudich















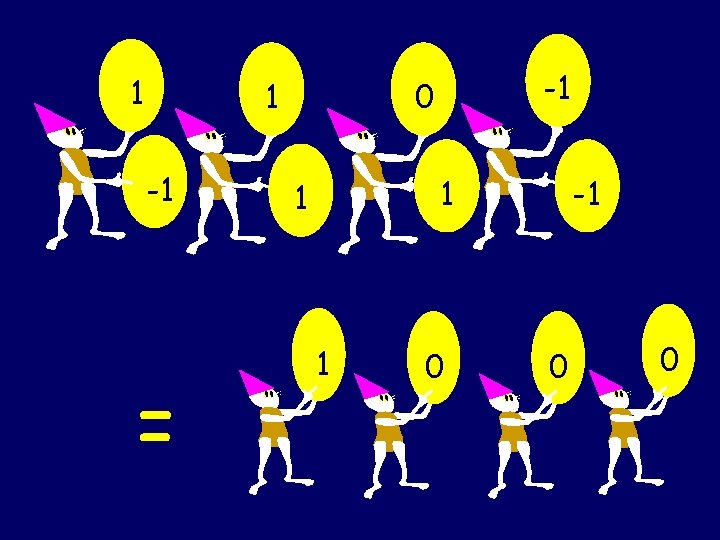




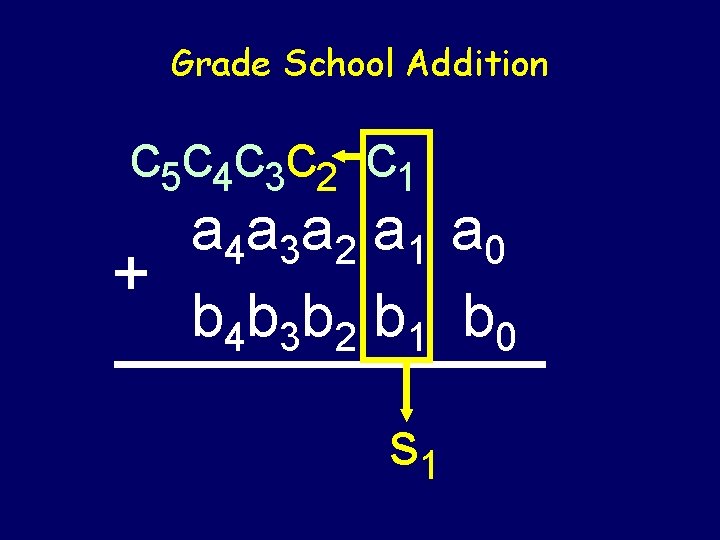















































- Slides: 98

Great Theoretical Ideas In Computer Science Steven Rudich Lecture 17 CS 15 -251 Mar 16, 2004 Spring 2004 Carnegie Mellon University Grade School Again: A Parallel Perspective

Plus/Minus Binary (Extended Binary) Base 2: Each digit can be -1, 0, 1, Example: 1 -1 -1 = 4 -2 -1 = 1

One weight for each power of 3. Left = “negative”. Right = “positive”

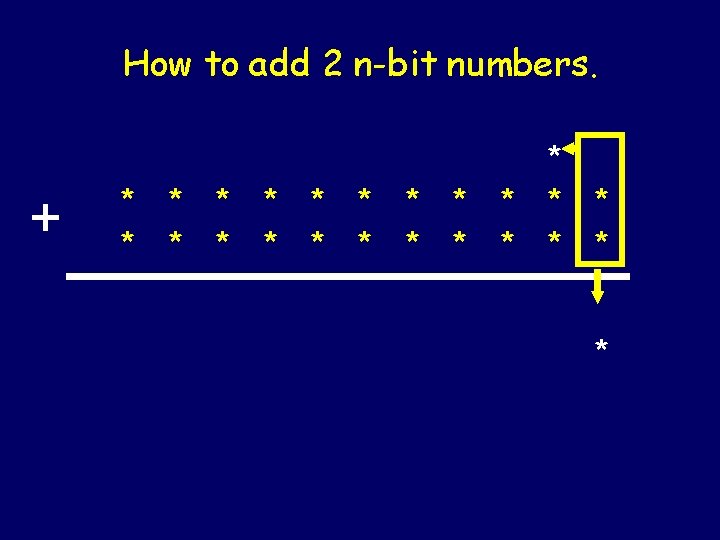
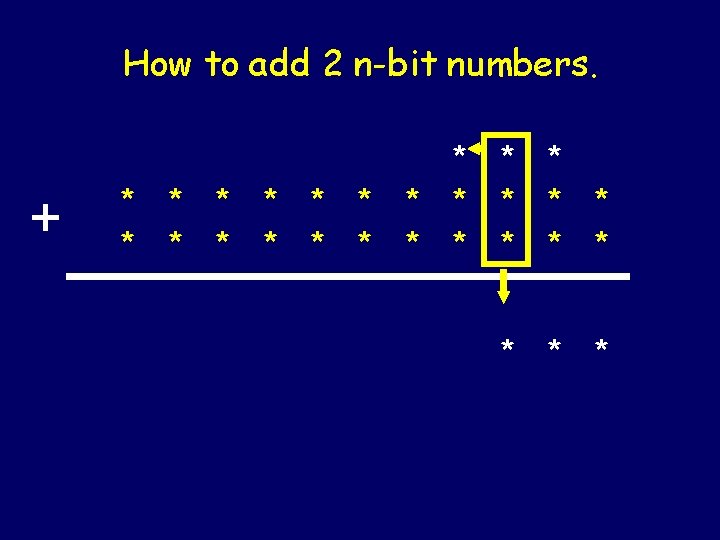
How to add 2 n-bit numbers. + * * * * * *

How to add 2 n-bit numbers. + * * * * * *

How to add 2 n-bit numbers. + * * * * * * *

How to add 2 n-bit numbers. + * * * * * * *

How to add 2 n-bit numbers. + * * * * * * * *

How to add 2 n-bit numbers. + * * * * * * * * * * * *

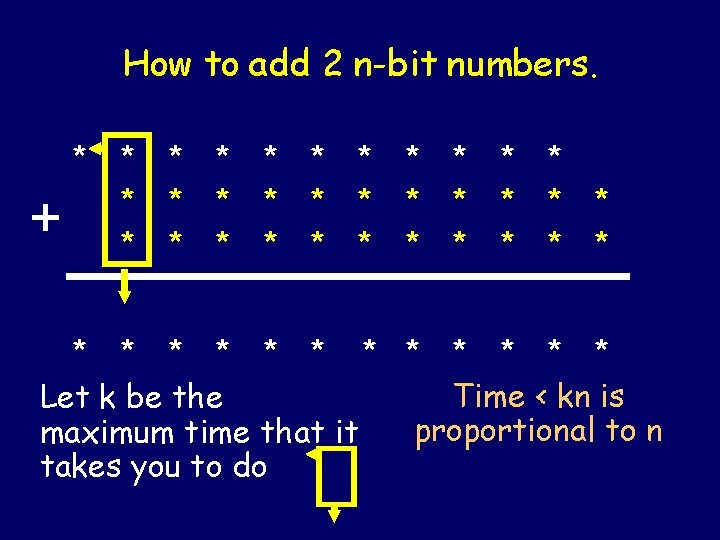
How to add 2 n-bit numbers. + * * * * * * * * * * Let k be the maximum time that it takes you to do * * * Time < kn is proportional to n

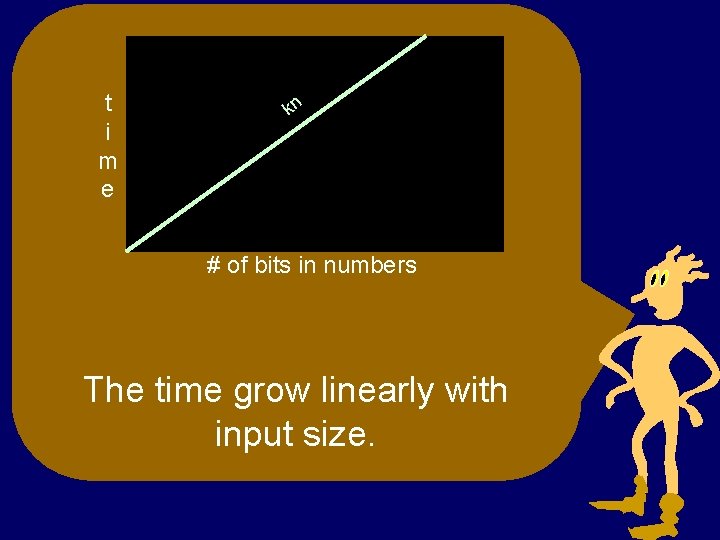
t i m e kn # of bits in numbers The time grow linearly with input size.

If n people agree to help you add two n bit numbers, it is not obvious that they can finish faster than if you had done it yourself.

Is it possible to add two n bit numbers in less than linear parallel-time? Darn those carries.

Fast parallel addition is no obvious in usual binary. But it is amazingly direct in Extended Binary!

Extended binary means base 2 allowing digits to be from {-1, 0, 1}. We can call each digit a “trit”.

n people can add 2, n-trit, plus/minus binary numbers in constant time!

An Addition Party to Add 110 -1 to -111 -1 -

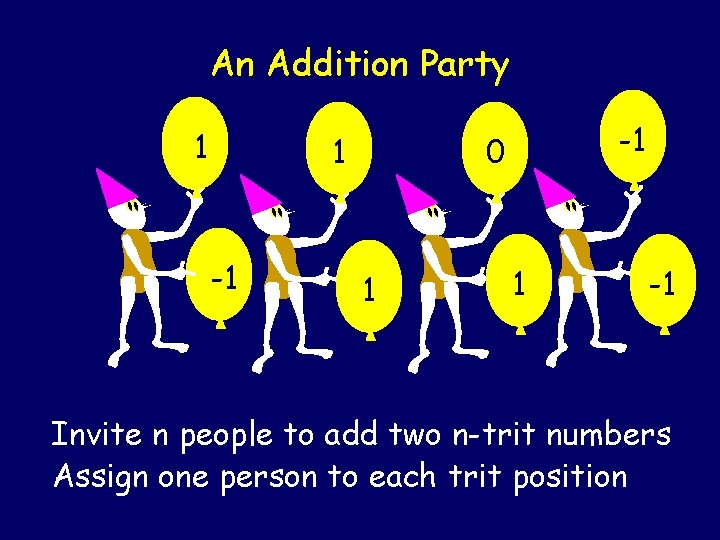
An Addition Party 1 1 -1 -1 0 1 1 -1 Invite n people to add two n-trit numbers Assign one person to each trit position

An Addition Party 0 2 1 0 -2 1 -1 1 Each person should add the two input trits in their possession. Problem: 2 and -2 are not allowed in the final answer.

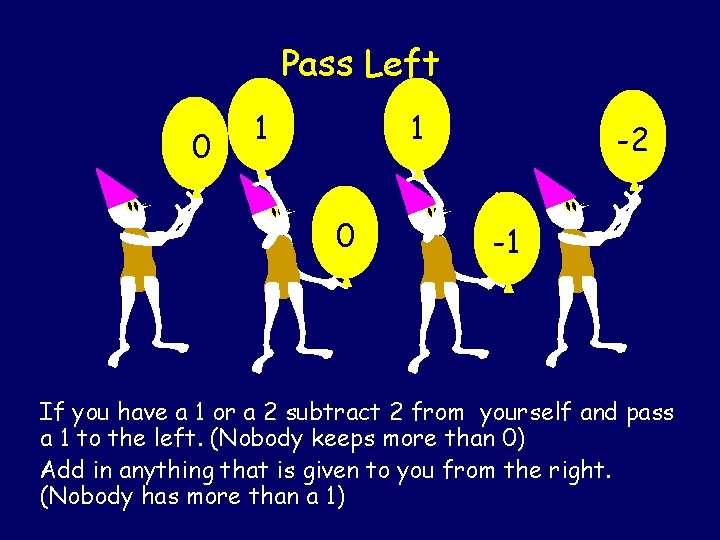
Pass Left 1 0 0 1 1 0 -2 -1 -1 If you have a 1 or a 2 subtract 2 from yourself and pass a 1 to the left. (Nobody keeps more than 0) Add in anything that is given to you from the right. (Nobody has more than a 1)

After passing left 1 1 0 -2 -1 1 There will never again be any 2 s as everyone had at most 0 and received at most 1 more

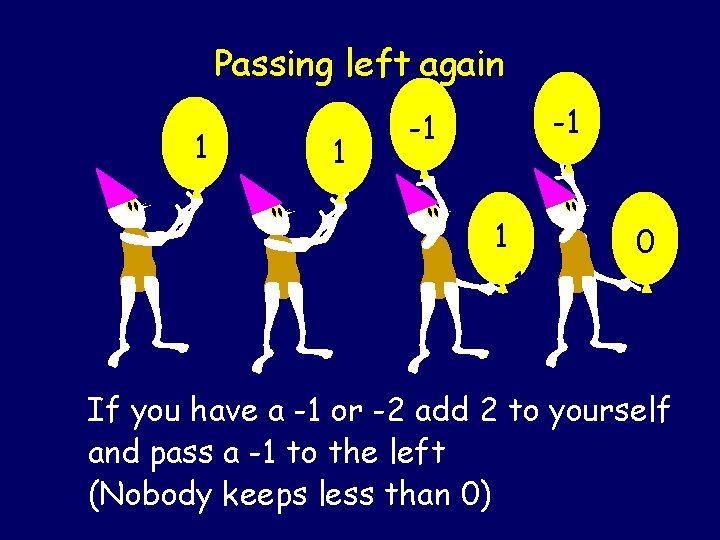
Passing left again 1 1 0 -1 -1 1 1 0 If you have a -1 or -2 add 2 to yourself and pass a -1 to the left (Nobody keeps less than 0)

After passing left again 1 0 0 -1 1 No -2 s anymore either. Everyone kept at least 0 and received At most -1.
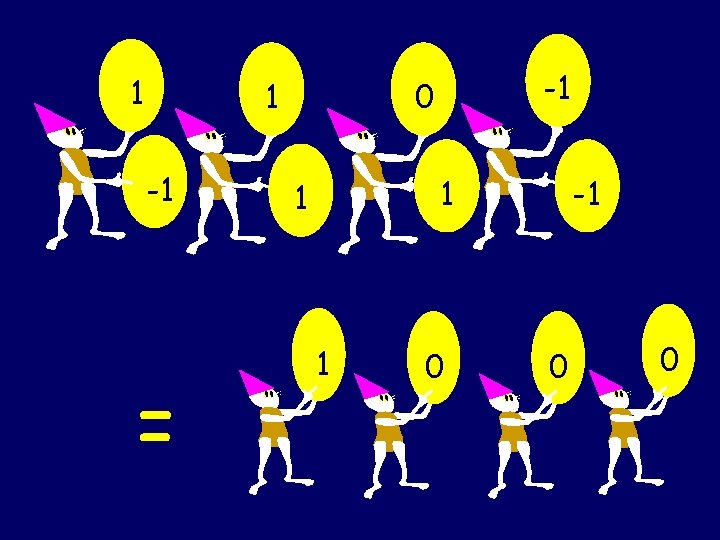
1 1 -1 = -1 0 1 1 1 0 1 -1 0 0 1 1

1 1 Caution: Parties and Algorithms Do not Mix 0 1 1

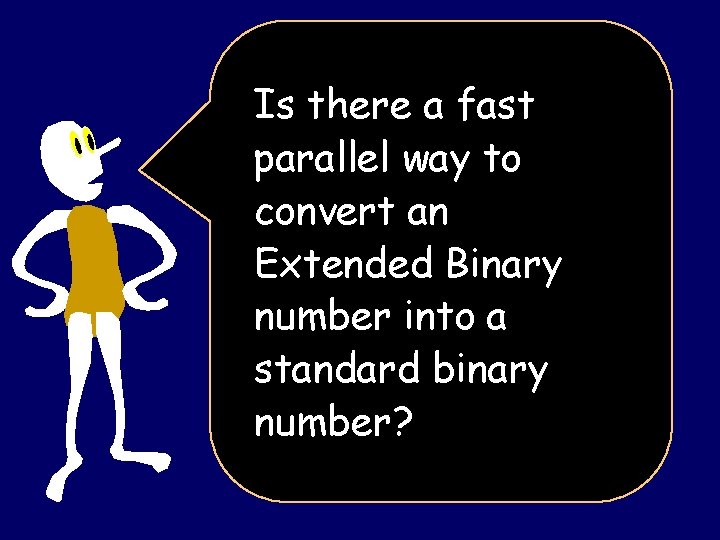
Is there a fast parallel way to convert an Extended Binary number into a standard binary number?

Not obvious: Sub-linear addition in standard Binary. Sub-linear EB to Binary

Let’s reexamine grade school addition from the view of a computer circuit.

Grade School Addition 1011111100 1011111101 + 1000000110 10100000011
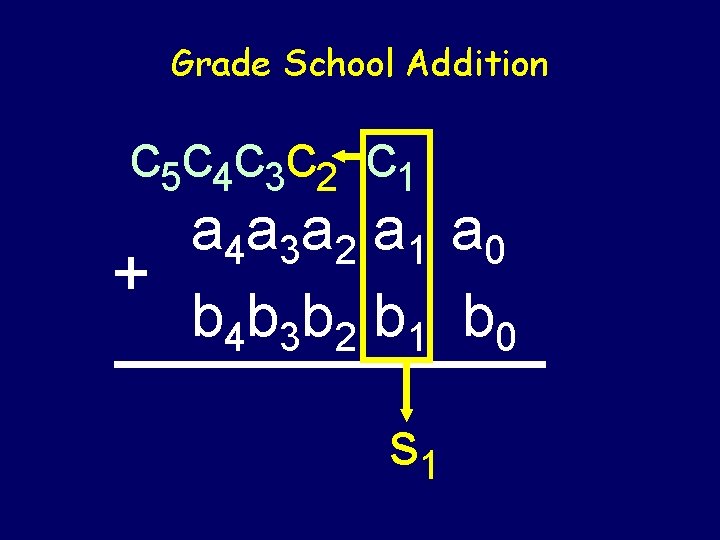
Grade School Addition c 5 c 4 c 3 c 2 c 1 a 4 a 3 a 2 a 1 a 0 + b 4 b 3 b 2 b 1 b 0 s 1

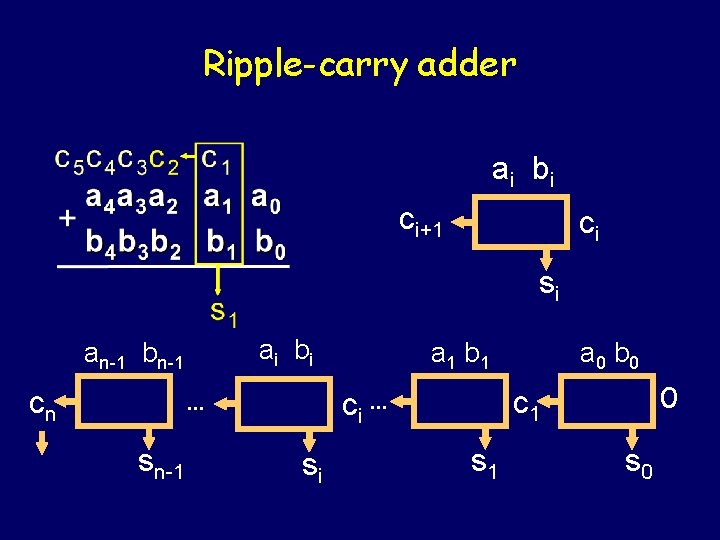
Ripple-carry adder ai b i ci+1 ci si ai b i an-1 bn-1 cn ci … … sn-1 a 1 b 1 si a 0 b 0 0 c 1 s 0

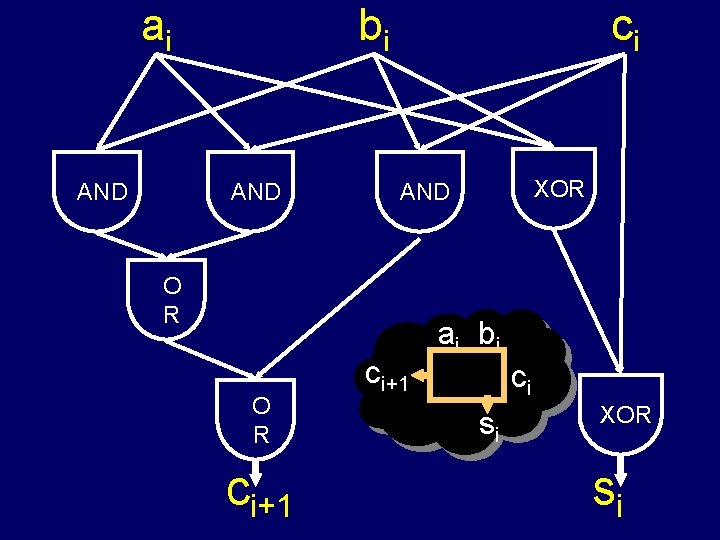
Logical representation of binary: 0 = false, 1 = true ai b i ci+1 ci si s 1 = (a 1 XOR b 1) XOR c 1 c 2 = (a 1 AND b 1) OR (a 1 AND c 1) OR (b 1 AND c 1)

ai AND bi AND ci O R ci+1 XOR AND ci+1 ai b i ci si XOR si

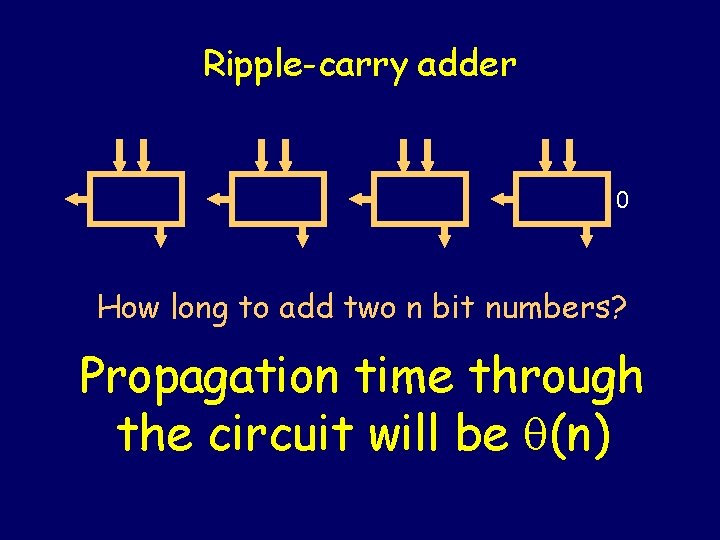
Ripple-carry adder 0 How long to add two n bit numbers? Propagation time through the circuit will be (n)

Circuits compute things in parallel. We can think of the propagation delay as PARALLEL TIME.

Is it possible to add two n bit numbers in less than linear parallel-time?

I suppose the EB addition algorithm could be helpful somehow.

Plus/minus binary means base 2 allowing digits to be from {-1, 0, 1}. We can call each digit a “trit”.

n people can add 2, n-trit, plus/minus binary numbers in constant time!

1 -1 1 0 1 1 -1 -1

Can we still do addition quickly in the standard representation?

Yes, but first a neat idea… Instead of adding two numbers to make one number, let’s think about adding 3 numbers to make 2 numbers.

Carry-Save Addition The sum of three numbers can be converted into the sum of 2 numbers in constant parallel time! 1100111011 + 1011111101 + 1000000110

Carry-Save Addition The sum of three numbers can be converted into the sum of 2 numbers in constant parallel time! 1100111011 + 1011111101 + 1000000110 1111000000 + 10001111110 XOR Carries

Cool! So if we if represent x as a+b, and y as c+d, then can add x, y using two of these (this is basically the same as that plus/minus binary thing). (a+b+c)+d=(e+f)+d=g+h

Even in standard representation, this is really useful for multiplication.

Grade School Multiplication X **** 101 1 0111 ******** ********

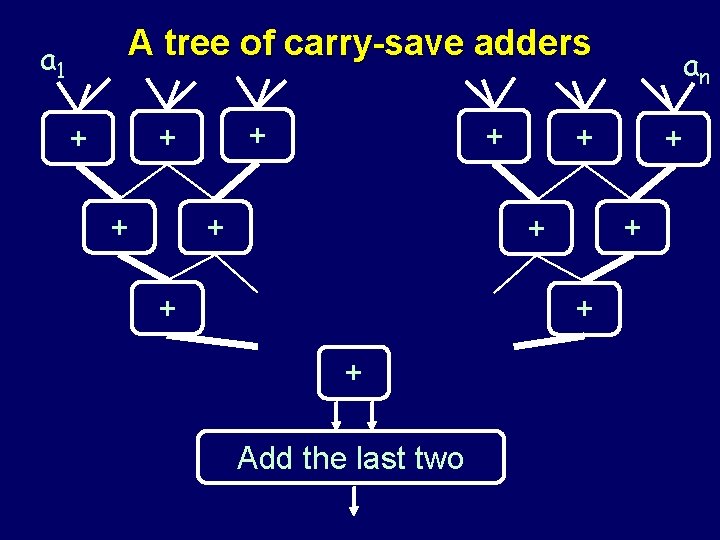
We need to add n 2 n-bit numbers: a 1, a 2, a 3, …, an

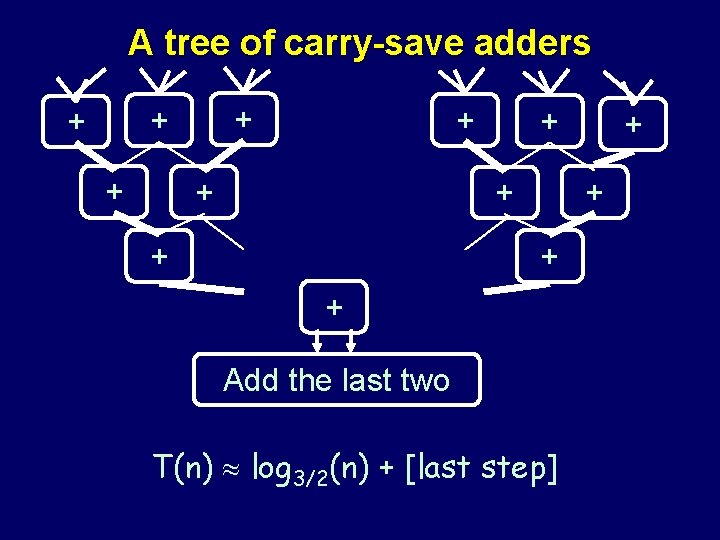
A tree of carry-save adders a 1 + + + + + Add the last two + + an

A tree of carry-save adders + + + + Add the last two T(n) log 3/2(n) + [last step]

So let’s go back to the problem of adding two numbers. In particular, if we can add two numbers in O(log n) parallel time, then we can multiply in O(log n) parallel time too!

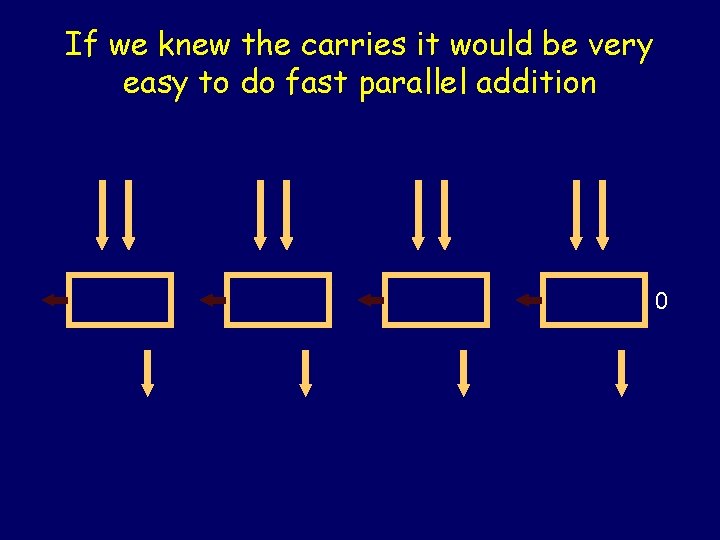
If we knew the carries it would be very easy to do fast parallel addition 0

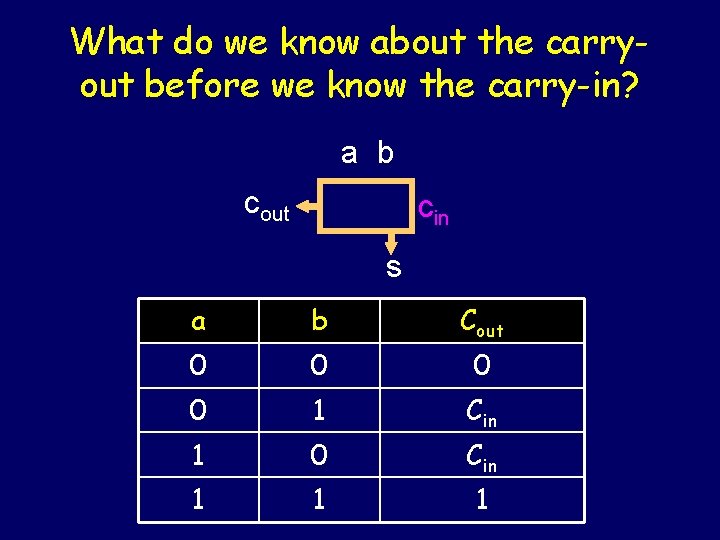
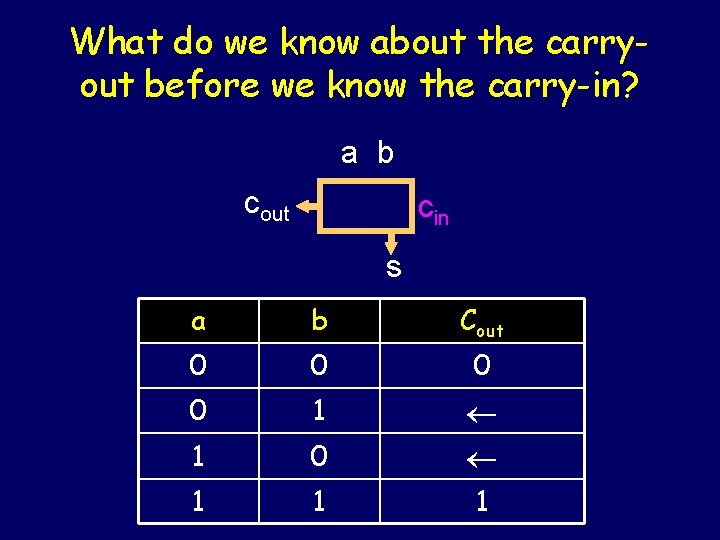
What do we know about the carryout before we know the carry-in? a b cout cin s a b Cout 0 0 1 Cin 1 0 Cin 1 1 1

What do we know about the carryout before we know the carry-in? a b cout cin s a b Cout 0 0 1 1 0 1 1 1

Hey, this is just a function of a and b. We can do this in parallel. a b Cout 0 0 1 1 0 1 1 1

Idea #1: do this calculation first. 10 1 0 1011111101 + 1000000110 This takes just one step!

Idea #1: do this calculation first. 10 1 0 1011111101 + 1000000110 Also, once we have the carries, it only takes one step more: si = (ai XOR bi) XOR ci

10 1 0 So, everything boils down to: can we find a fast parallel way to convert each position to its final 0/1 value? Called the “parallel prefix problem”

10 1 0 So, we need to do this quickly….

Idea #2: 10 1 0 as all Can think of partial results in: (1 (0 ( (1 ( 0))))) for the operator : x = x 1 x=1 0 x=0 0 1 0 0 0 1 1 1 0 1

Idea #2 (cont): And, the operator is associative. 10 1 0 ( (1 ( 0))))) = ( ) ( 1) ( 0) = 1 0 = 1

Just using the fact that we have an Associative, Binary Operator: an operation that takes two objects and returns a third. • A B = C Associative: • (A B) C=A (B C)

Examples • • Addition on the integers Min(a, b) Max(a, b) Left(a, b) = a Right(a, b) = b Boolean AND Boolean OR •

In what we are about to do “+” will mean an arbitrary binary associative operator.

Prefix Sum Problem Input: Xn-1, Xn-2, …, X 1, X 0 Output: Yn-1, Yn-2, …, Y 1, Y 0 where Y 0 = X 0 Y 1 = X 0 + X 1 Y 2 = X 0 + X 1 + X 2 Y 3 = X 0 + X 1 + X 2 + X 3. . . Yn-1 = X 0 + X 1 + X 2 + X 3 + … + Xn-1

Prefix Sum example Input: 6, 9, 2, 3, 4, 7 Output: 31, 25, 16, 14, 11, 7 where Y 0 = X 0 Y 1 = X 0 + X 1 Y 2 = X 0 + X 1 + X 2 Y 3 = X 0 + X 1 + X 2 + X 3. . . Yn-1 = X 0 + X 1 + X 2 + X 3 + … + Xn-1

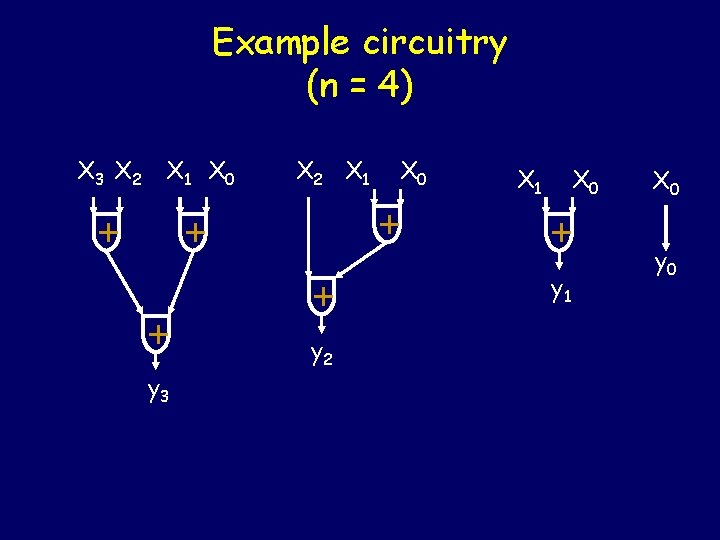
Example circuitry (n = 4) X 3 X 2 X 1 X 0 + + + y 3 X 2 X 1 X 0 + + y 2 X 1 X 0 + y 1 X 0 y 0

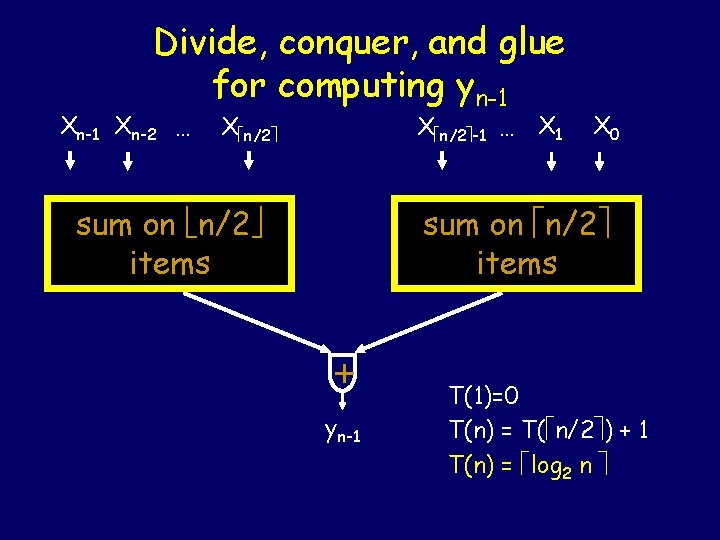
Divide, conquer, and glue for computing yn-1 Xn-2 … X n/2 -1 … X 1 X n/2 sum on n/2 items X 0 sum on n/2 items + yn-1 T(1)=0 T(n) = T( n/2 ) + 1 T(n) = log 2 n

Modern computers do something slightly different. This algorithm is fast, but how many components does it use?

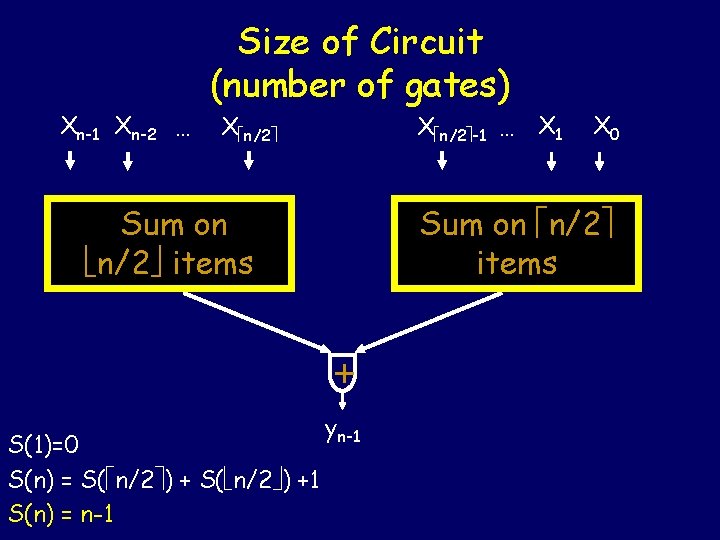
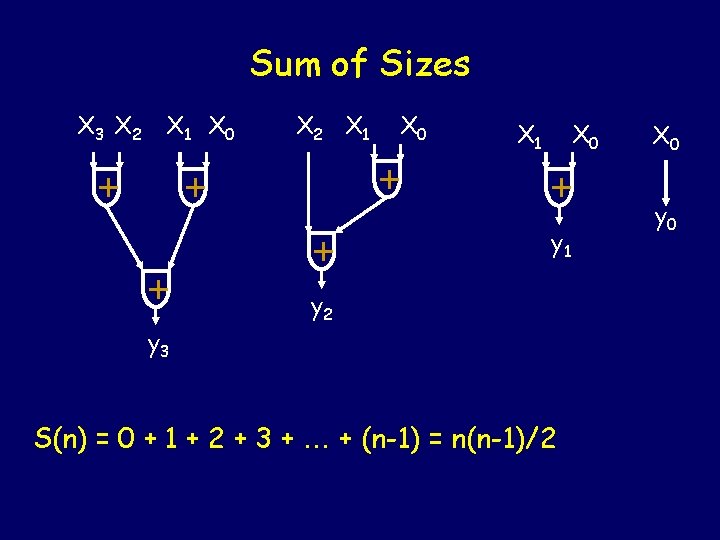
Size of Circuit (number of gates) Xn-1 Xn-2 … X n/2 -1 … X 1 X n/2 Sum on n/2 items + S(1)=0 S(n) = S( n/2 ) +1 S(n) = n-1 X 0 yn-1

Sum of Sizes X 3 X 2 X 1 X 0 + + + y 3 X 2 X 1 X 0 + + X 1 X 0 + y 1 y 2 S(n) = 0 + 1 + 2 + 3 + + (n-1) = n(n-1)/2 X 0 y 0

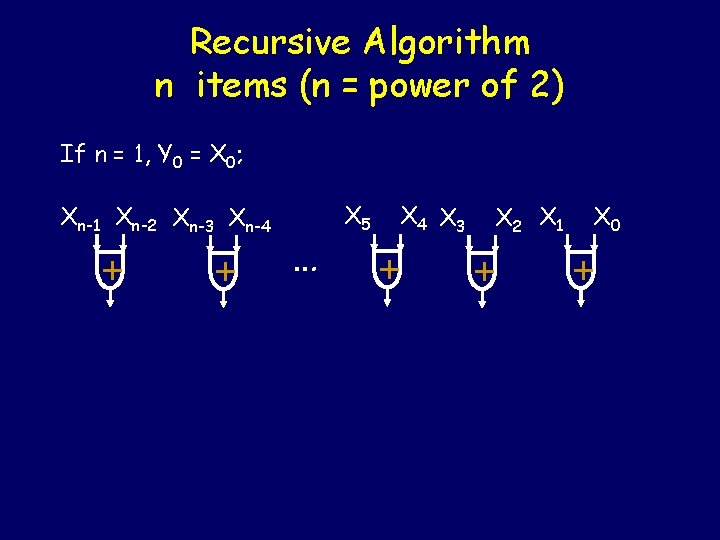
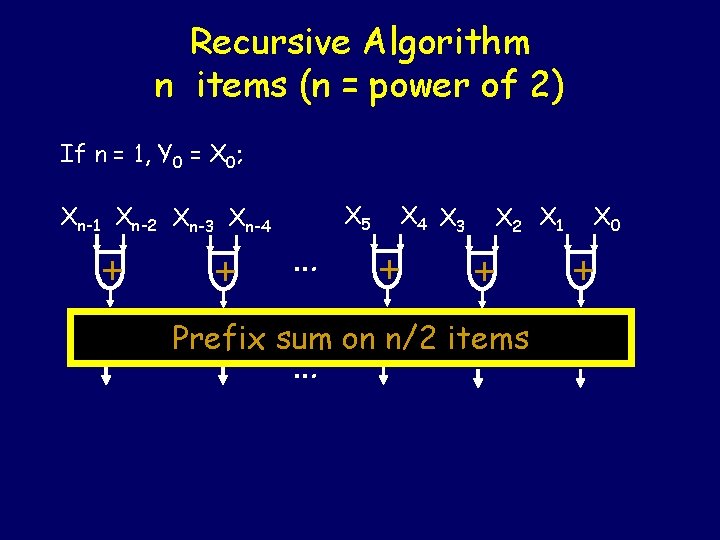
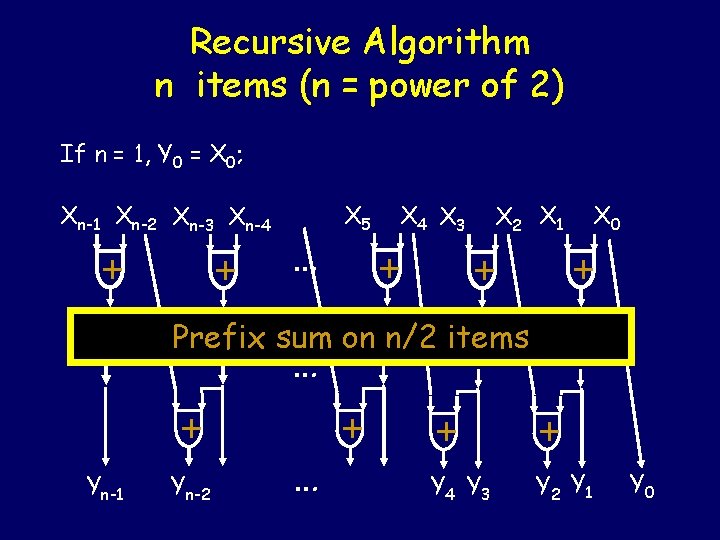
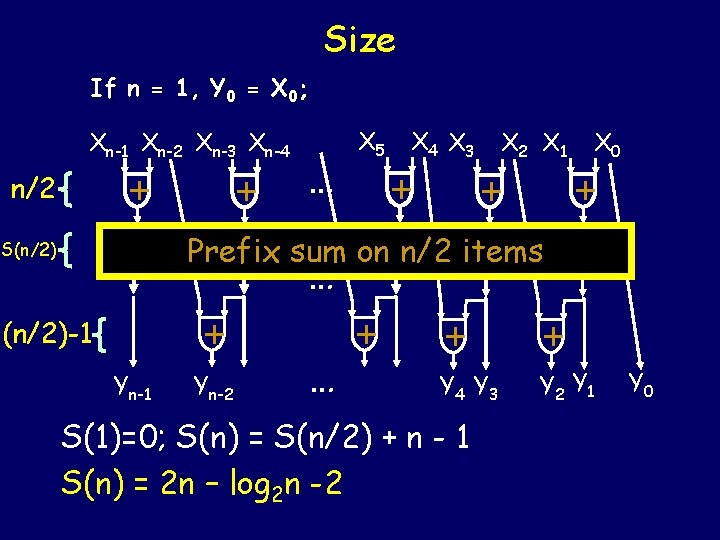
Recursive Algorithm n items (n = power of 2) If n = 1, Y 0 = X 0; Xn-1 Xn-2 Xn-3 Xn-4 + + … X 5 X 4 X 3 + X 2 X 1 + X 0 +

Recursive Algorithm n items (n = power of 2) If n = 1, Y 0 = X 0; Xn-1 Xn-2 Xn-3 Xn-4 + + … X 5 X 4 X 3 + X 2 X 1 + Prefix sum on n/2 items … X 0 +

Recursive Algorithm n items (n = power of 2) If n = 1, Y 0 = X 0; Xn-1 Xn-2 Xn-3 Xn-4 + + … X 5 X 4 X 3 + X 2 X 1 X 0 + + Prefix sum on n/2 items … + Yn-1 Yn-2 … + + + Y 4 Y 3 Y 2 Y 1 Y 0

Parallel time complexity If n = 1, Y 0 = X 0; Xn-1 Xn-2 Xn-3 Xn-4 1 + + … X 5 X 4 X 3 + X 2 X 1 X 0 + + Prefix sum on n/2 items T(n/2) … 1 + Yn-1 Yn-2 … + + + Y 4 Y 3 Y 2 Y 1 T(1)=0; T(2) = 1; T(n) = T(n/2) + 2 T(n) = 2 log 2(n) - 1 Y 0

Size If n = 1, Y 0 = X 0; Xn-1 Xn-2 Xn-3 Xn-4 n/2 + + … X 5 X 4 X 3 + X 2 X 1 X 0 + + Prefix sum on n/2 items S(n/2) … (n/2)-1 + Yn-1 Yn-2 … + + + Y 4 Y 3 Y 2 Y 1 S(1)=0; S(n) = S(n/2) + n - 1 S(n) = 2 n – log 2 n -2 Y 0

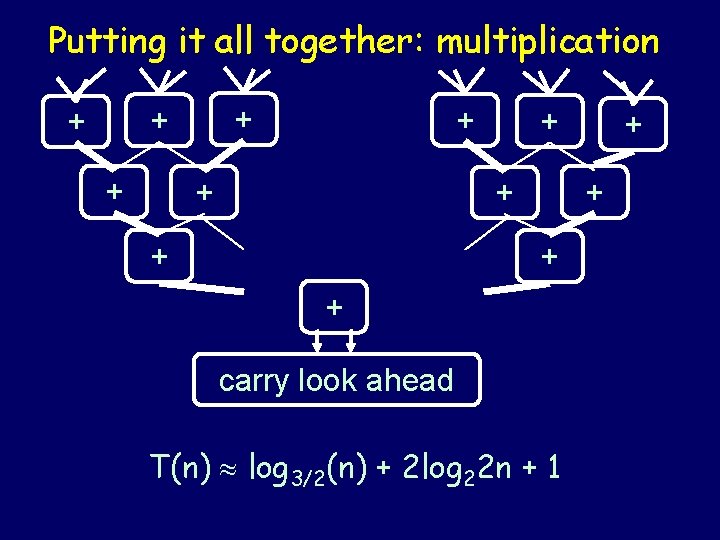
Putting it all together: Carry Look. Ahead Addition To add two n-bit numbers: a and b • 1 step to compute x values ( 01 ) • 2 log 2 n - 1 steps to compute carries c • 1 step to compute c XOR (a XOR b) 2 log 2 n + 1 steps total

Putting it all together: multiplication + + + + carry look ahead T(n) log 3/2(n) + 2 log 22 n + 1

For a 64 -bit word that works out to a parallel time of 22 for multiplication, and 13 for addition.

s e r i u q e r n o e i t m i s i d a t d h r A inea t u b 1 l , + y l l n a 2 i g t o n l. e 2 u m l q se ctica orith a lg r a p l a lle a r pa

ch i h w ( n io t r a e c i d r s pl a i a t h h l lot ) also Mu a is ly time l a i t n ). e n u m g q (lo gorith se O an el al ll a r pa

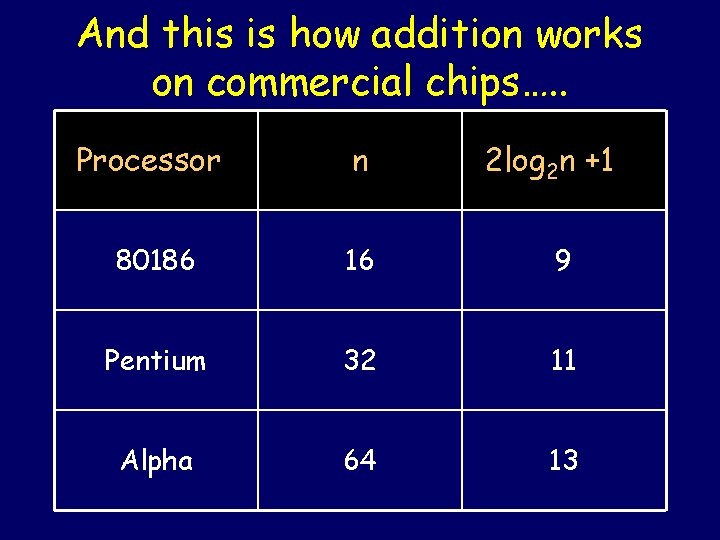
And this is how addition works on commercial chips…. . Processor n 2 log 2 n +1 80186 16 9 Pentium 32 11 Alpha 64 13

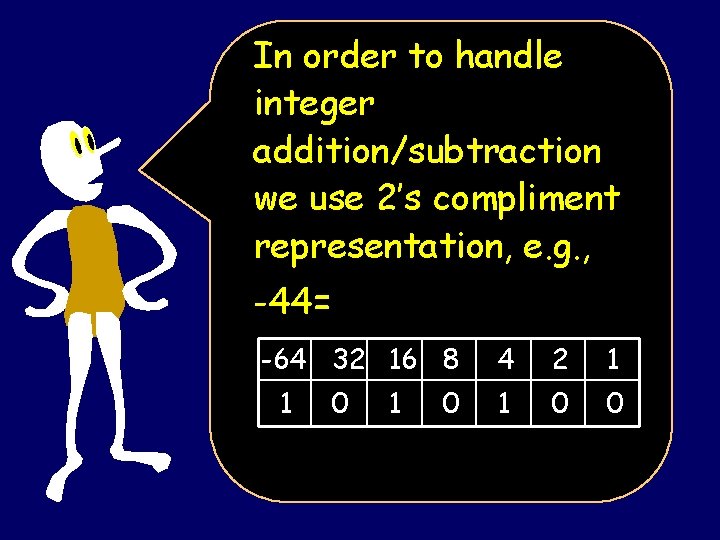
In order to handle integer addition/subtraction we use 2’s compliment representation, e. g. , -44= -64 32 16 8 1 0 4 2 1 1 0 0

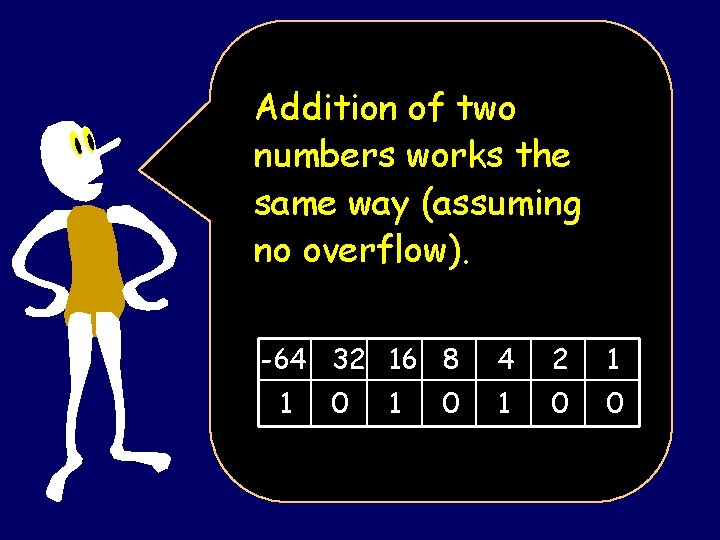
Addition of two numbers works the same way (assuming no overflow). -64 32 16 8 1 0 4 2 1 1 0 0

To negate a number, flip each of its bits and add 1. -64 1 -64 0 32 16 8 4 2 1 0 0 32 16 8 4 2 1 1 1 0 1 1 32 16 8 4 2 1 1 1 0 0 1

To negate a number, flip each of its bits and add 1. -64 1 32 16 8 4 2 1 1 1 1 x + flip(x) = -1. So, -x = flip(x)+1.

Most computers use two’s compliment representation to perform integer addition and subtraction.

Grade School Division ******** ******** ******** n bits of precision: n subtractions costing 2 log 2 n + 1 each (n logn)

Let’s see if we can reduce to O(n) by being clever about it.

Idea: internally, allow ourselves to “go negative” using trits so we can do constant-time subtraction. Then convert back at the end. (technically, called “extended binary”)

SRT division algorithm 1 1 -1 1 0 r – 1 1 1 0 1 -1 0 – 1 -1 1 0 – 1 1 -1 0 – 1 -1 -2 0 = -1 0 0 1 1 01 1 1 2 =1 0 0 0 -1 0 – 1 – 1 1 22 r -5 21 r 6 11 237 Rule: Each bit of quotient is determined by comparing first bit of divisor with first bit of dividend. Easy! Time for n bits of precision in result: 3 n + 2 log 2(n) + 1 1 addition per bit Convert to standard representation by subtracting negative bits from positive.

Intel Pentium division error • The Pentium uses essentially the same algorithm, but computes more than one bit of the result in each step. Several leading bits of the divisor and quotient are examined at each step, and the difference is looked up in a table. • The table had several bad entries. • Ultimately Intel offered to replace any defective chip, estimating their loss at $475 million.

If millions of processors, how much of a speed-up might I get over a single processor?

Brent’s Law At best, p processors will give you a factor of p speedup over the time it takes on a single processor.

The traditional GCD algorithm will take linear time to operate on two n bit numbers. Can it be done faster in parallel?

If n 2 people agree to help you compute the GCD of two n bit numbers, it is not obvious that they can finish faster than if you had done it yourself.

D C G y Is l t n e r e ? l h a n i i t n e u q se

No one knows.
 Steven rudich
Steven rudich Great theoretical ideas in computer science
Great theoretical ideas in computer science Great theoretical ideas in computer science
Great theoretical ideas in computer science Great theoretical ideas in computer science
Great theoretical ideas in computer science Great theoretical ideas in computer science
Great theoretical ideas in computer science Great theoretical ideas in computer science
Great theoretical ideas in computer science Great theoretical ideas in computer science
Great theoretical ideas in computer science Vocabularize
Vocabularize Great theoretical ideas in computer science
Great theoretical ideas in computer science Great theoretical ideas in computer science
Great theoretical ideas in computer science Jeff rudich
Jeff rudich Great ideas in computer science
Great ideas in computer science Graph theory cs
Graph theory cs Addressing mode in computer architecture
Addressing mode in computer architecture Task level parallelism
Task level parallelism 8 great ideas in computer architecture
8 great ideas in computer architecture 8 great ideas in computer architecture
8 great ideas in computer architecture My favorite subject is maths
My favorite subject is maths Ideas have consequences bad ideas have victims
Ideas have consequences bad ideas have victims Los deseos ridículos preguntas y respuestas
Los deseos ridículos preguntas y respuestas China big idea
China big idea Science national honor society project ideas
Science national honor society project ideas National children's science congress projects ideas
National children's science congress projects ideas Turning great strategy into great performance
Turning great strategy into great performance South dakota state symbols
South dakota state symbols Leadership comes with great responsibility
Leadership comes with great responsibility Hammerhead shark vs great white shark
Hammerhead shark vs great white shark Does alexander the great deserve his title
Does alexander the great deserve his title Enlightened despot catherine
Enlightened despot catherine With great expectations comes great responsibility
With great expectations comes great responsibility A great deal vs a great many
A great deal vs a great many With great power comes great responsibility
With great power comes great responsibility Does alexander deserve to be called the great
Does alexander deserve to be called the great Great is thy faithfulness o lord my father
Great is thy faithfulness o lord my father Great explorations in math and science
Great explorations in math and science Social science vs natural science
Social science vs natural science Six branches of science
Six branches of science Natural and physical science
Natural and physical science Applied science vs pure science
Applied science vs pure science Rapid change
Rapid change Extra credit
Extra credit Tragedy of the commons
Tragedy of the commons Windcube
Windcube Soft science definition
Soft science definition Steven khoury ministries
Steven khoury ministries Sharon kroll
Sharon kroll Dr steven copp
Dr steven copp Steven mair westminster
Steven mair westminster Carol lynn benson
Carol lynn benson Sexual attraction
Sexual attraction Googlenomics
Googlenomics Steven benini
Steven benini Steven izenour
Steven izenour Steven johnson menular atau tidak
Steven johnson menular atau tidak Dr steven kahn
Dr steven kahn Steven kyle cornell
Steven kyle cornell Steven walchek
Steven walchek Steven boyce md
Steven boyce md Bakit mahalagang magkaroon ng tamang direksyon sa buhay?
Bakit mahalagang magkaroon ng tamang direksyon sa buhay? Resectoscopie
Resectoscopie Steven quilos mortais
Steven quilos mortais Steven hustinx
Steven hustinx Hsc geography notes
Hsc geography notes Steven briggs ucsd
Steven briggs ucsd Harry williams lmhc
Harry williams lmhc Steven spewak
Steven spewak Steven unikewicz
Steven unikewicz Steven unikewicz
Steven unikewicz Elixir roadmap
Elixir roadmap Konnektionismus spracherwerb
Konnektionismus spracherwerb Facts about antonin artaud
Facts about antonin artaud Ufic stem opt
Ufic stem opt Arpanet
Arpanet Steven stanko
Steven stanko Asic
Asic Dr steven goldin
Dr steven goldin Connie valenzuela
Connie valenzuela Wood lane medical center
Wood lane medical center Steven tuomi,
Steven tuomi, Steven tamm salesforce
Steven tamm salesforce Steven berkowitz md
Steven berkowitz md Rick kuntz
Rick kuntz Steven cunnane
Steven cunnane Steven tam md
Steven tam md Seacoast water utility
Seacoast water utility Dr steven goldin
Dr steven goldin Dr steven kahn
Dr steven kahn Steven rudick md
Steven rudick md Steven fang
Steven fang Steven paul jobs biography
Steven paul jobs biography Steven abramowitz
Steven abramowitz Steven p. wallace
Steven p. wallace Steven pemberton css
Steven pemberton css Steven fang
Steven fang Steven johnson everything bad is good for you
Steven johnson everything bad is good for you Steven reiss
Steven reiss Steven lemos
Steven lemos Dr steven goldin
Dr steven goldin Dr steven kahn
Dr steven kahn