Introduction Credits Steve Rudich Jeff Edmond Ping Xuan






















































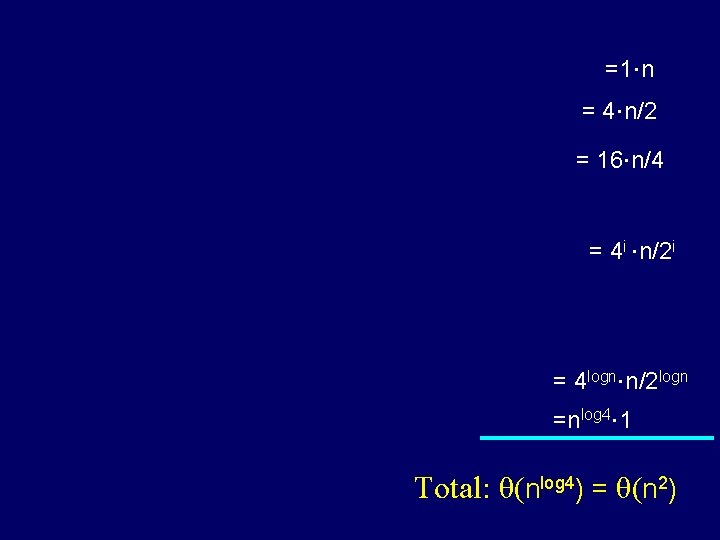







- Slides: 91

Introduction Credits: Steve Rudich, Jeff Edmond, Ping Xuan

• So you want to be a bioinformatician /mathematician /computer scientist? • What is an Algorithm ? • Grade school revisited: How to multiply two numbers

So you want to be a computer scientist?

Is your goal to be a mundane programmer?

Or a great leader and thinker?

Original Thinking

Boss assigns task: – Given today’s prices of pork, grain, sawdust, … – Given constraints on what constitutes a hotdog. – Make the cheapest hotdog. Everyday industry asks these questions.

Your answer: • Um? Tell me what to code. With more suffocated software engineering systems, the demand for mundane programmers will diminish.

Your answer: • I learned this great algorithm that will work. Soon all known algorithms will be available in libraries.

Your answer: • I can develop a new algorithm for you. Great thinkers will always be needed.

The future belongs to the computer scientist who has – Content: An up to date grasp of fundamental problems and solutions – Method: Principles and techniques to solve the vast array of unfamiliar problems that arise in a rapidly changing field

Course Content • A list of algoirthms. – Learn their code. – Trace them until you are convenced that they work. class Insertion. Sort. Algorithm extends Sort. Algorithm { – Impliment them. void sort(int a[]) throws Exception { for (int i = 1; i < a. length; i++) { int j = i; int B = a[i]; while ((j > 0) && (a[j-1] > B)) { a[j] = a[j-1]; j--; } a[j] = B; }}

Course Content • A survey of algorithmic design techniques. • Abstract thinking. • How to develop new algorithms for any problem that may arise.

Study: • Many experienced programmers were asked to code up binary search.

Study: • Many experienced programmers were asked to code up binary search. 80% got it wrong Good thing is was not for a nuclear power plant.

What did they lack?

What did they lack? • Formal proof methods?

What did they lack? • Formal proof methods? Yes, likely Industry is starting to realize that formal methods are important. But even without formal methods …. ?

What did they lack? • Fundamental understanding of the algorithmic design techniques. • Abstract thinking.

Course Content Notations, analogies, and abstractions for developing, thinking about, and describing algorithms

You will see some Math … Time Complexity t(n) = (n 2) Recurrence Relations T(n) = a T(n/b) + f(n)

What is an Algorithm? p A step-by-step description of procedures performing certain task. n Example: Sorting. Given a list of numbers, put them in increasing (non-decreasing) order. p Properties: Generality, Termination, Correctness, Feasibility. p Feasibility Analysis of Algorithm Complexity theory

Analysis of Algorithm p Running time analysis n n Input size N Running time is a function of N: T(N) Worst case, average case, … , etc p Time measured by number of computer operations p § Each basic operation (add, load, write, etc) count as 1 Actual clock time differs by a constant factor p Usually very complex p n The use of asymptotic bounds To study the rate of growth of T(N) compared to simpler functions f(N), such as N, N 2, log(N), etc p A constant factor can be ignored p

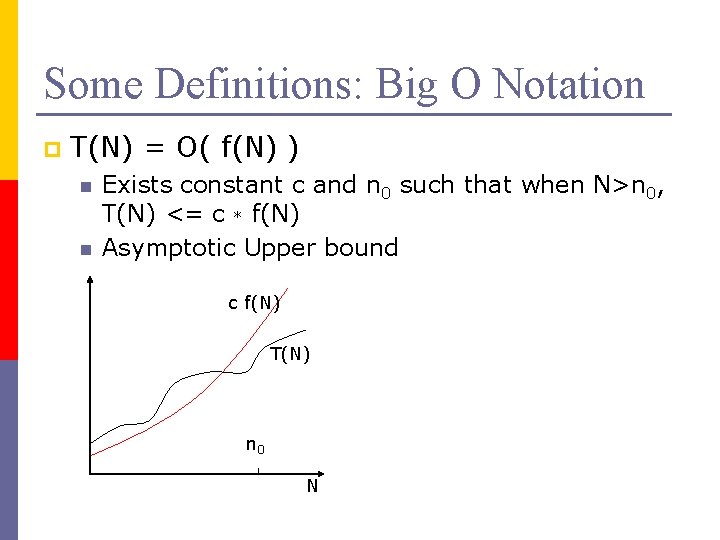
Some Definitions: Big O Notation p T(N) = O( f(N) ) n n Exists constant c and n 0 such that when N>n 0, T(N) <= c * f(N) Asymptotic Upper bound c f(N) T(N) n 0 N

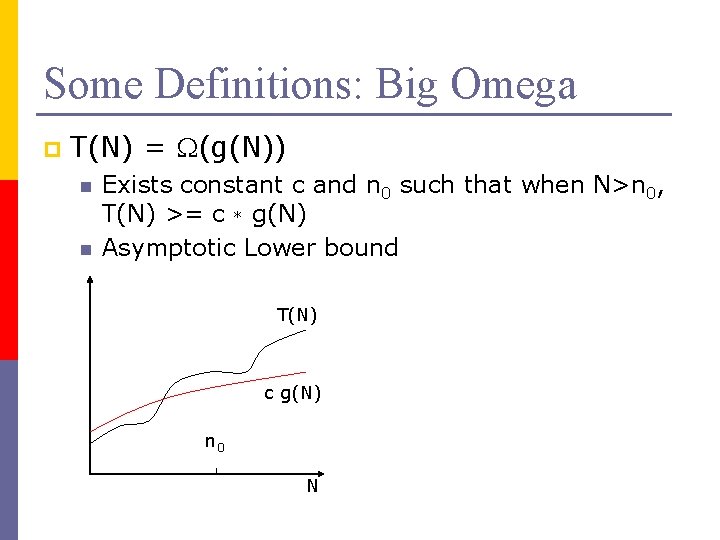
Some Definitions: Big Omega p T(N) = (g(N)) n n Exists constant c and n 0 such that when N>n 0, T(N) >= c * g(N) Asymptotic Lower bound T(N) c g(N) n 0 N

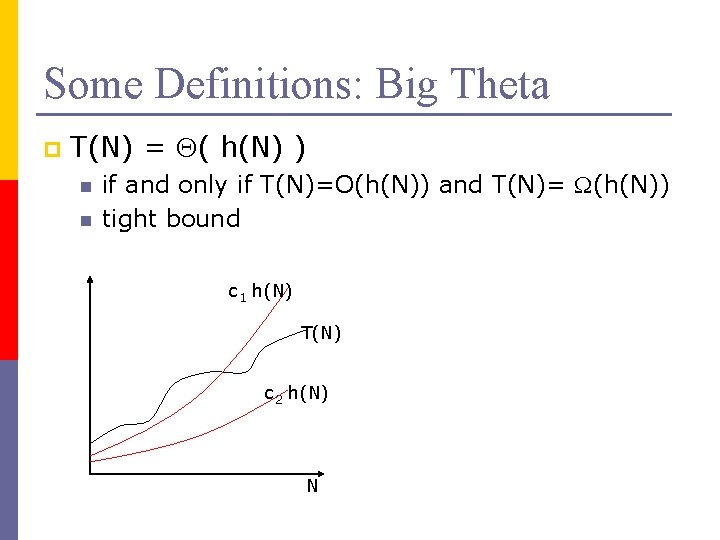
Some Definitions: Big Theta p T(N) = ( h(N) ) n n if and only if T(N)=O(h(N)) and T(N)= (h(N)) tight bound c 1 h(N) T(N) c 2 h(N) N

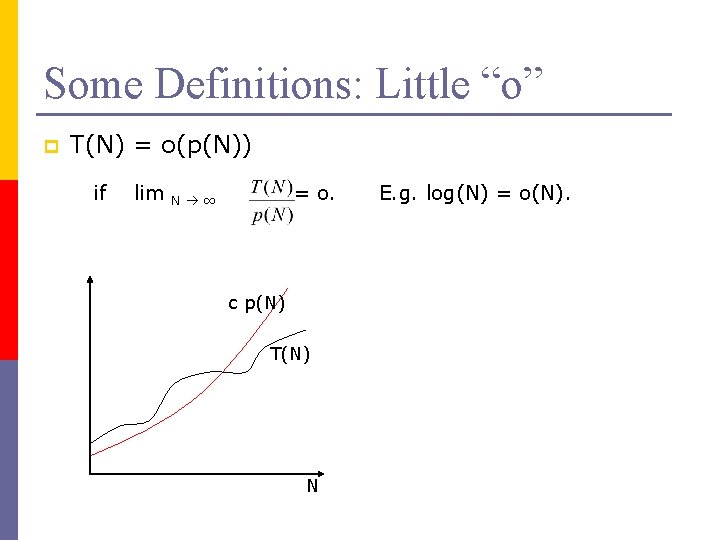
Some Definitions: Little “o” p T(N) = o(p(N)) if lim = o. N ∞ c p(N) T(N) N E. g. log(N) = o(N).

Example: Insertion Sort Algorithm class Insertion. Sort. Algorithm extends Sort. Algorithm { p void sort(int a[ ]) throws Exception { p for (int i = 1; i < a. length; i++) { p int j = i; p int B = a[i]; p while ((j > 0) && (a[j-1] > B)) { p a[j] = a[j-1]; p j--; } p a[j] = B; p }} p

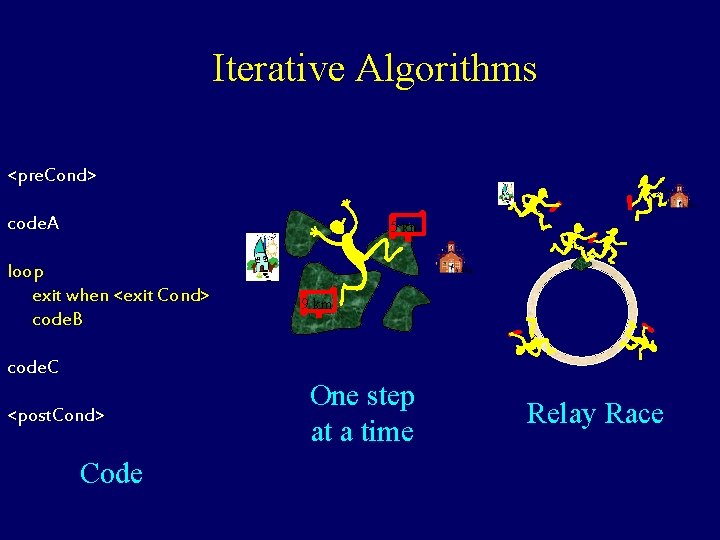
Iterative Algorithms <pre. Cond> 1 T+ 0 code. A 5 km i-1 loop exit when <exit Cond> code. B 9 km i <post. Cond> Code One step at a time i code. C i Relay Race

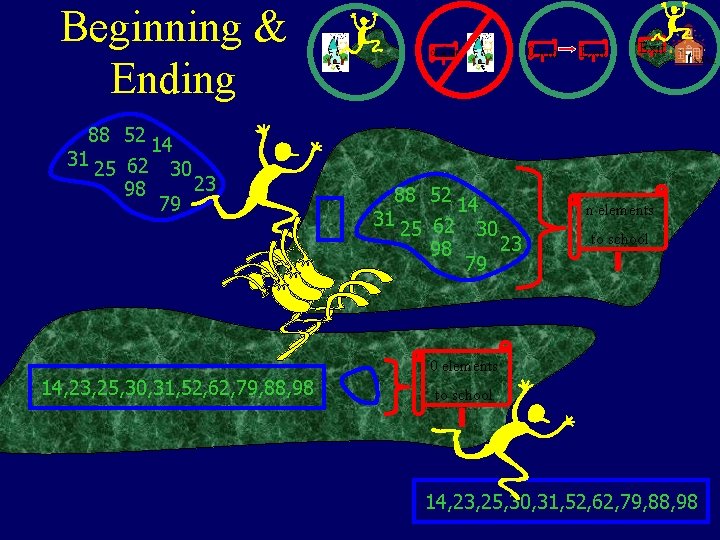
Problem Specification • Precondition: The input is a list of n values with the same value possibly repeated. • Post condition: The output is a list consisting of the same n values in non-decreasing order. 88 52 14 31 25 98 30 23 62 79 14, 23, 25, 30, 31, 52, 62, 79, 88, 98

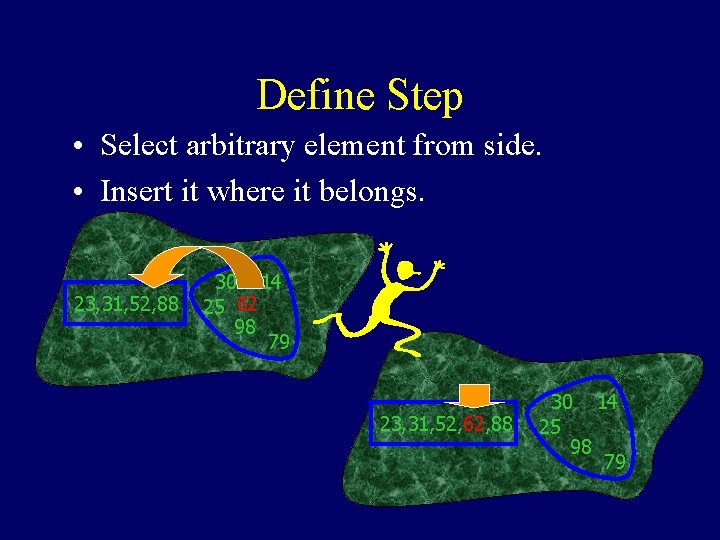
Define Step • Select arbitrary element from side. • Insert it where it belongs. 23, 31, 52, 88 30 14 25 62 98 79 23, 31, 52, 62, 88 30 14 25 98 79

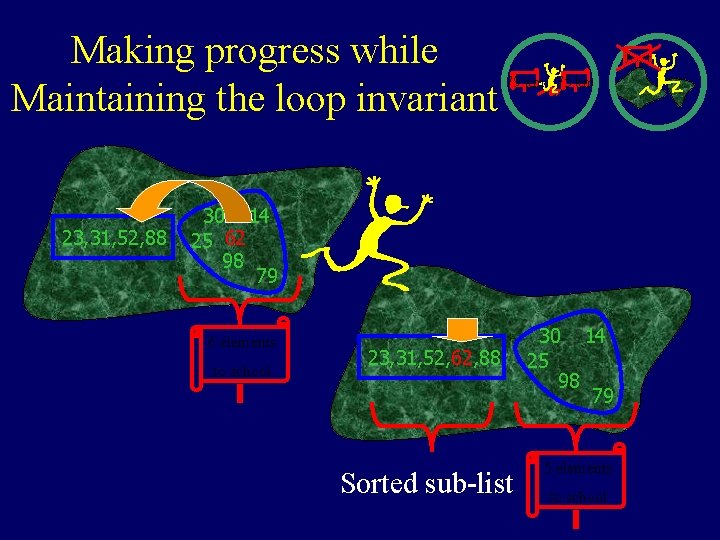
Making progress while Maintaining the loop invariant 23, 31, 52, 88 Exit 79 km 75 km 30 14 25 62 98 79 6 elements to school 23, 31, 52, 62, 88 Sorted sub-list 30 14 25 98 79 5 elements to school

Beginning & Ending 88 52 14 31 25 62 30 23 98 79 0 km 88 52 14 31 25 62 30 23 98 79 Exit n elements to school 0 elements 14, 23, 25, 30, 31, 52, 62, 79, 88, 98 to school 14, 23, 25, 30, 31, 52, 62, 79, 88, 98

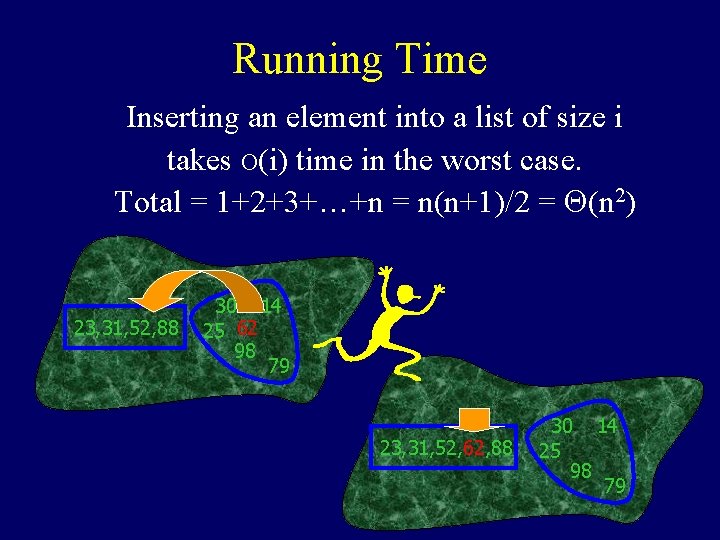
Running Time Inserting an element into a list of size i takes O(i) time in the worst case. Total = 1+2+3+…+n = n(n+1)/2 = (n 2) 23, 31, 52, 88 30 14 25 62 98 79 23, 31, 52, 62, 88 30 14 25 98 79

Explaining Insertion Sort We maintain a subset of elements sorted within a list. The remaining elements are off to the side somewhere. Initially, think of the first element in the array as a sorted list of length one. One at a time, we take one of the elements that is off to the side and we insert it into the sorted list where it belongs. This gives a sorted list that is one element longer than it was before. When the last element has been inserted, the array is completely sorted.

Insertion Sort The input consists of an array of integers 52, 23, 88, 31, 25, 30, 98, 62, 14, 79 23, 31, 52, 88 23, 25, 31, 52, 88 We read in the i+1 st object. We will pretend that this larger prefix is the entire input. We extend the solution we have by one for this larger prefix.

Insertion Sort Algorithm: Pseudo-Code p Input: an array (or list) a of numbers // data structure: a[0] … a[n-1] a 0 p 1 2 n-1 Operations: n n Leave the first element (location 0) untouched. for each element from location 1 on insert it to the appropriate place in the (sorted) sub-array to its left.

Operations in an Algorithm p Decision Making n n p branching operation if … then … else … Repetition n n loops: for each element do { … } conditional loops: while ( …. ) do { … }

Insertion Sort Algorithm: Code class Insertion. Sort. Algorithm extends Sort. Algorithm { p void sort(int a[ ]) throws Exception { p for (int i = 1; i < a. length; i++) { p int j = i; p int b = a[i]; p while ( (j > 0) && (a[j-1] > b) ) { p a[j] = a[j-1]; p j--; } p a[j] = B; p }}} p

Another Algorithm Grade School Revisited: How To Multiply Two Numbers 2 X 2=5

Complex Numbers • Remember how to multiply 2 complex numbers? • (a+bi)(c+di) = [ac –bd] + [ad + bc] i • Input: a, b, c, d Output: ac-bd, ad+bc • If a real multiplication costs $1 and an addition cost a penny. What is the cheapest way to obtain the output from the input? • Can you do better than $4. 02?

Gauss’ $3. 05 Method: Input: a, b, c, d Output: ac-bd, ad+bc • m 1 = ac • m 2 = bd • A 1 = m 1 – m 2 = ac-bd • m 3 = (a+b)(c+d) = ac + ad + bc + bd • A 2 = m 3 – m 1 – m 2 = ad+bc

Question: • The Gauss “hack” saves one multiplication out of four. It requires 25% less work. • Could there be a context where performing 3 multiplications for every 4 provides a more dramatic savings?

Odette Bonzo

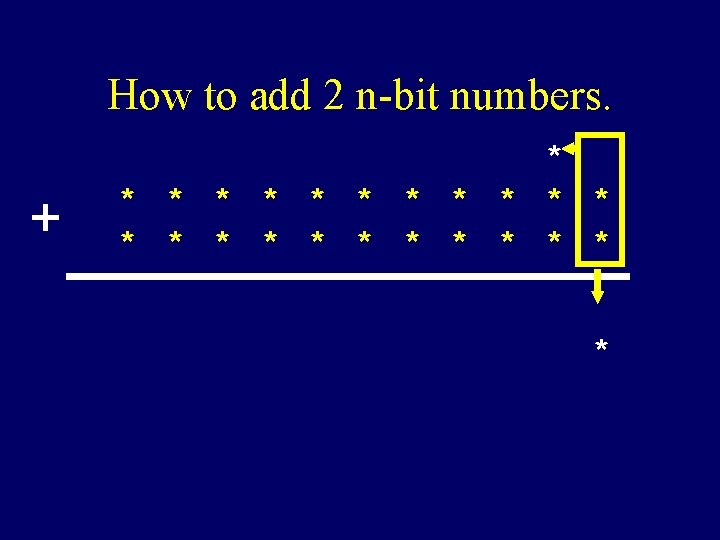
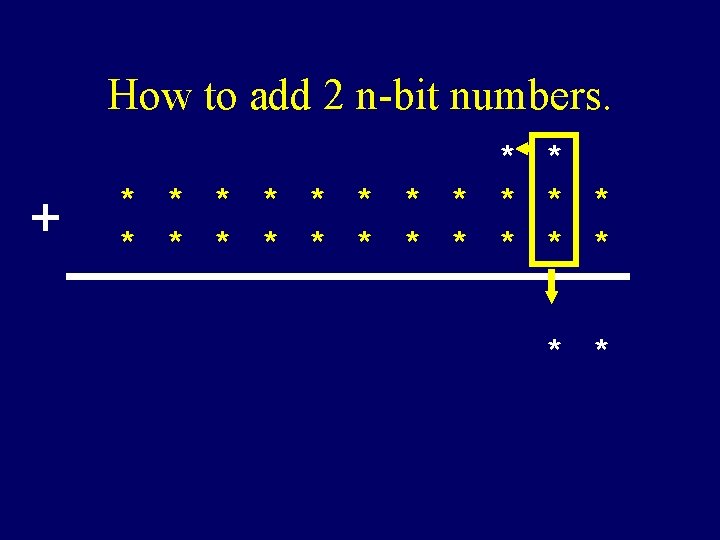
How to add 2 n-bit numbers. + * * * * * *

How to add 2 n-bit numbers. + * * * * * *

How to add 2 n-bit numbers. + * * * * * * *

How to add 2 n-bit numbers. + * * * * * * *

How to add 2 n-bit numbers. + * * * * * * * *

How to add 2 n-bit numbers. + * * * * * * * * * * * *

Time complexity of grade school addition * * * + ****** * * On any reasonable computer adding 3 bits can be done in constant time. * * * T(n) = The amount of time grade school addition uses to add two n-bit numbers = θ(n) = linear time.

f = θ(n) means that f can be sandwiched between two lines t i m e # of bits in numbers

Please feel free to ask questions!

Is there a faster way to add? • QUESTION: Is there an algorithm to add two n-bit numbers whose time grows sublinearly in n?

Any algorithm for addition must read all of the input bits – Suppose there is a mystery algorithm that does not examine each bit – Give the algorithm a pair of numbers. There must be some unexamined bit position i in one of the numbers – If the algorithm is not correct on the numbers, we found a bug – If the algorithm is correct, flip the bit at position i and give the algorithm the new pair of numbers. It give the same answer as before so it must be wrong since the sum has changed

So any algorithm for addition must use time at least linear in the size of the numbers. Grade school addition is essentially as good as it can be.

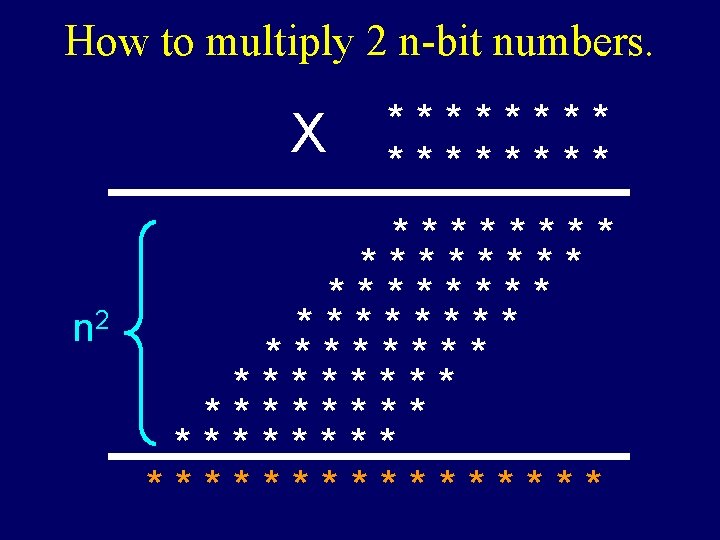
How to multiply 2 n-bit numbers. X n 2 ******** ******** ********

I get it! The total time is bounded by cn 2.

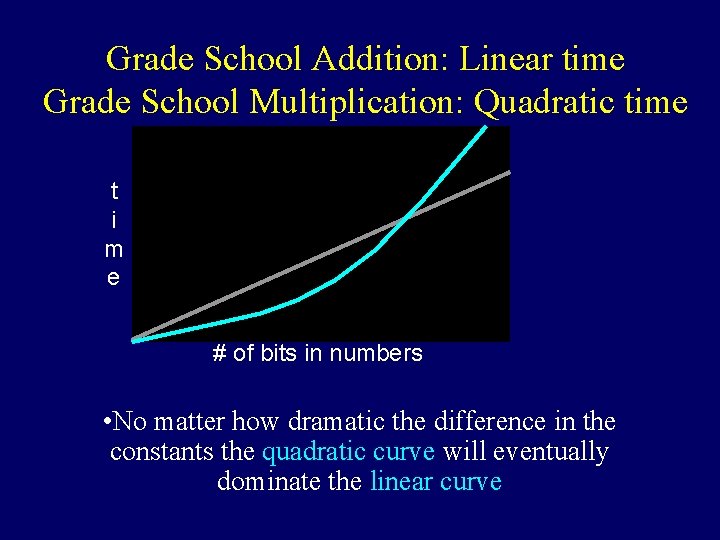
Grade School Addition: Linear time Grade School Multiplication: Quadratic time t i m e # of bits in numbers • No matter how dramatic the difference in the constants the quadratic curve will eventually dominate the linear curve

Neat! We have demonstrated that multiplication is a harder problem than addition. Mathematical confirmation of our common sense.

Don’t jump to conclusions! We have argued that grade school multiplication uses more time than grade school addition. This is a comparison of the complexity of two algorithms. To argue that multiplication is an inherently harder problem than addition we would have to show that no possible multiplication algorithm runs in linear time.

Grade School Addition: θ(n) time Grade School Multiplication: θ(n 2) time Is there a clever algorithm to multiply two numbers in linear time?

Despite years of research, no one knows! If you resolve this question, Tunghai will give you a Ph. D!

Is there a faster way to multiply two numbers than the way you learned in grade school?

Divide and Conquer (an approach to faster algorithms) • DIVIDE my instance to the problem into smaller instances to the same problem. • Have a friend (recursively) solve them. Do not worry about it yourself. • GLUE the answers together so as to obtain the answer to your larger instance.

Multiplication of 2 n-bit numbers • X= • Y= a b c d • X = a 2 n/2 + b Y = c 2 n/2 + d • XY = ac 2 n + (ad+bc) 2 n/2 + bd

Multiplication of 2 n-bit numbers a b • X= c d • Y= • XY = ac 2 n + (ad+bc) 2 n/2 + bd MULT( X, Y ) : If |X| = |Y| = 1 then RETURN XY Break X into a; b and Y into c; d RETURN MULT(a, c) 2 n + (MULT(a, d) + MULT(b, c)) 2 n/2 + MULT(b, d)

Time required by MULT • T( n ) = time taken by MULT on two n-bit numbers • What is T(n)? What is its growth rate? Is it θ(n 2)?

Recurrence Relation • T(1) = k for some constant k • T(n) = 4 T(n/2) + k n + l for some constants k and l MULT(X, Y): If |X| = |Y| = 1 then RETURN XY Break X into a; b and Y into c; d RETURN MULT(a, c) 2 n + (MULT(a, d) + MULT(b, c)) 2 n/2 + MULT(b, d)

Let’s be concrete • T(1) = 1 • T(n) = 4 T(n/2) + n • How do we unravel T(n) so that we can determine its growth rate?

Technique 1 Guess and Verify • Recurrence Relation: T(1) = 1 & T(n) = 4 T(n/2) + n • Guess: G(n) = 2 n 2 – n • Verify: Left Hand Side Right Hand Side T(1) = 2(1)2 – 1 T(n) = 2 n 2 – n 1 4 T(n/2) + n = 4 [2(n/2)2 – (n/2)] + n = 2 n 2 – n

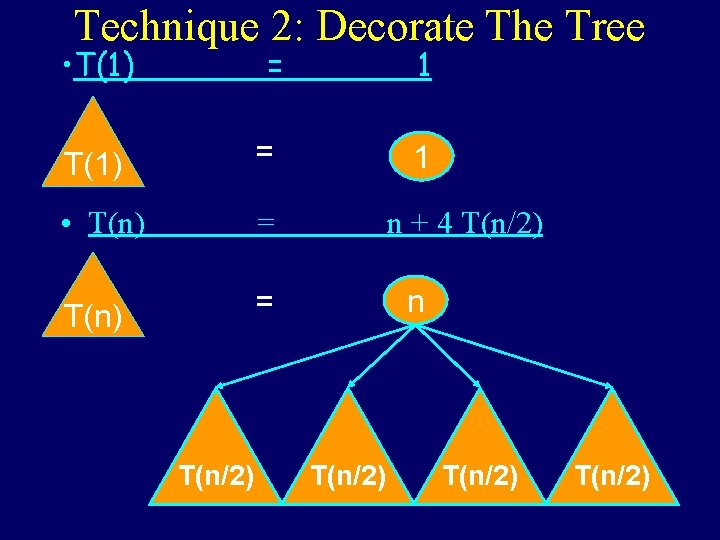
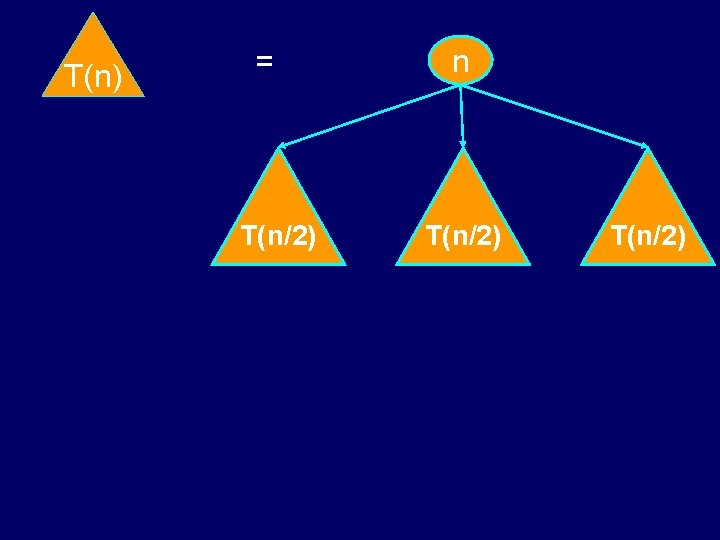
Technique 2: Decorate The Tree • T(1) = • T(n) = T(n/2) 1 1 n + 4 T(n/2) n T(n/2)

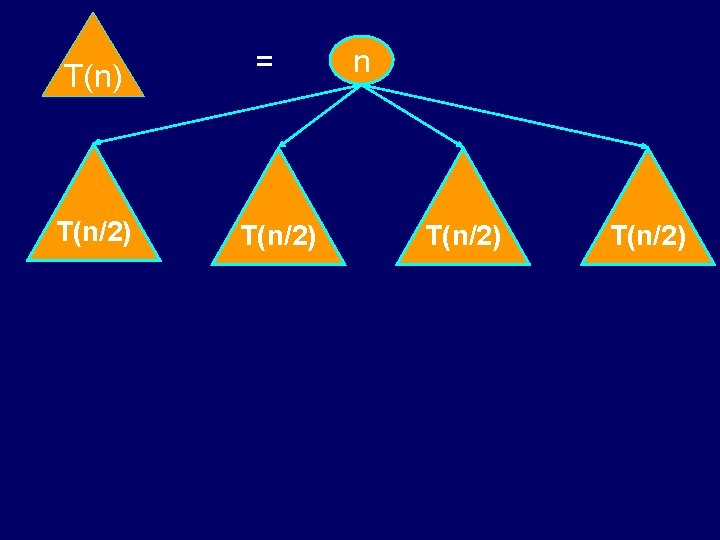
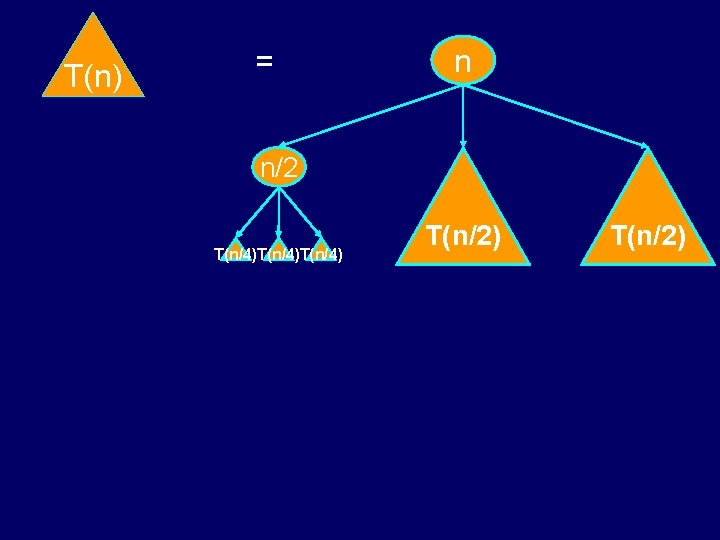
T(n) T(n/2) = T(n/2) n T(n/2)

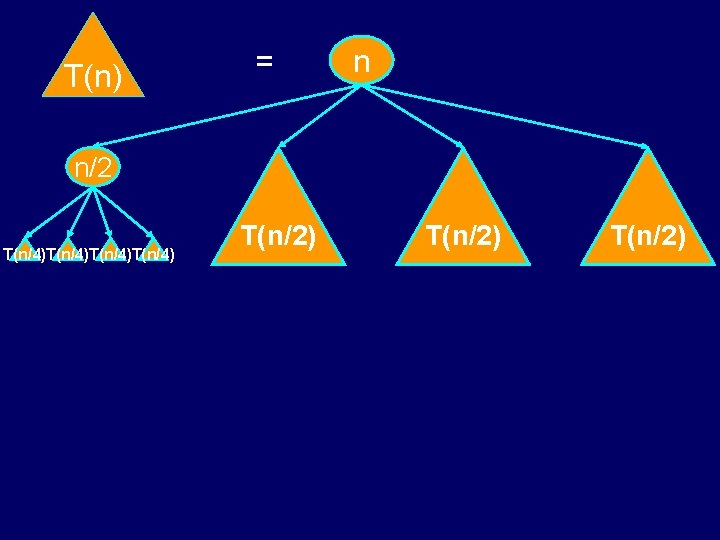
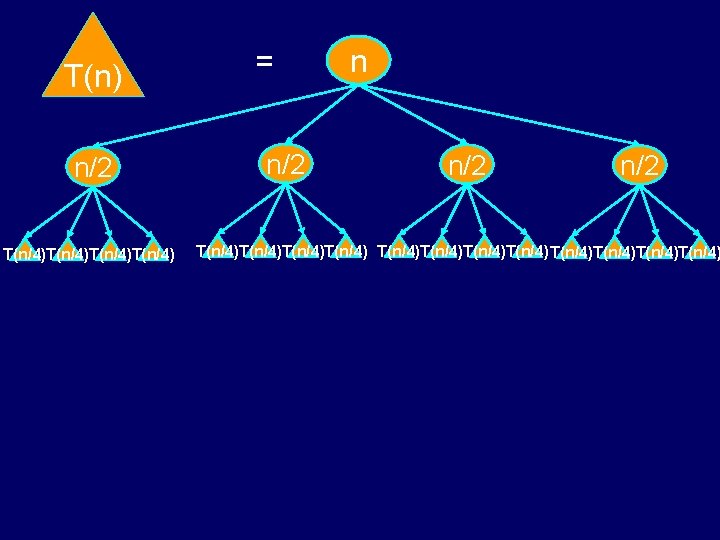
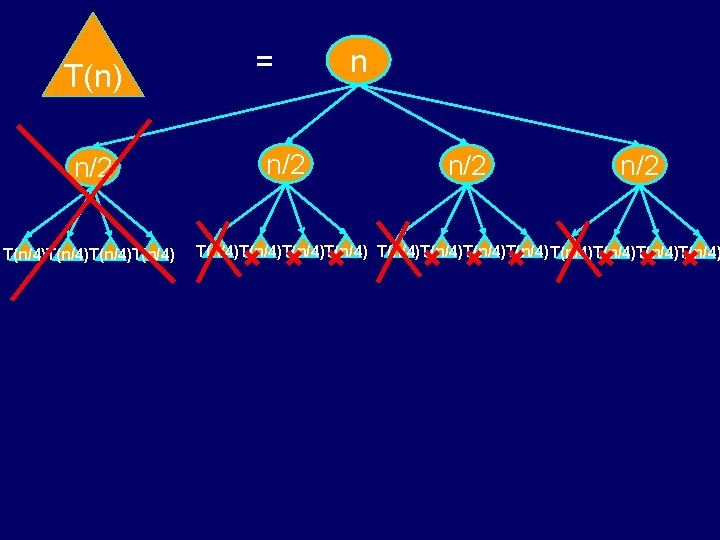
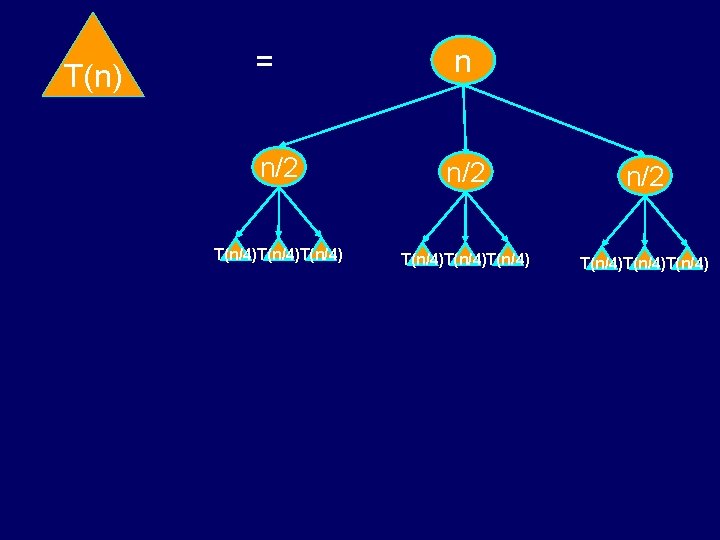
T(n) = n n/2 T(n/4)T(n/4) T(n/2)

T(n) n/2 T(n/4)T(n/4) = n/2 n/2 T(n/4)T(n/4)T(n/4)T(n/4)

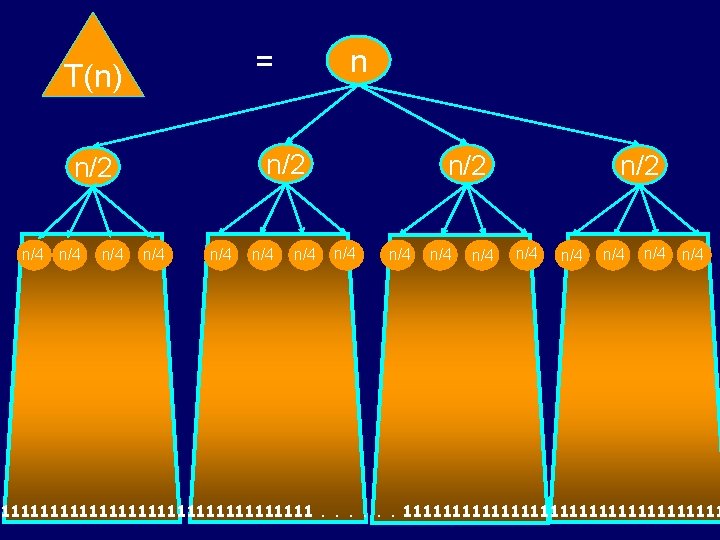
T(n) n/2 n/4 n/4 n = n/4 n/4 n/2 n/4 n/4 n/4 1111111111111111. . . 11111111111111111

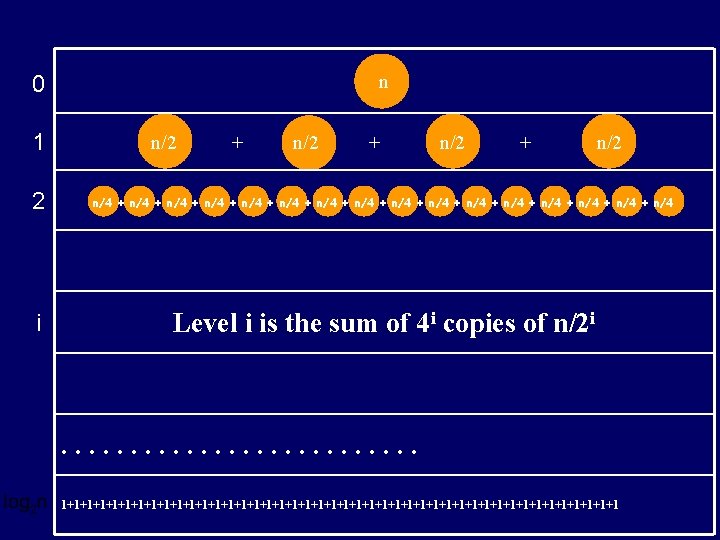
n 0 1 n/2 + n/2 2 n/4 + n/4 + n/4 + n/4 + n/4 i Level i is the sum of 4 i copies of n/2 i . . . 1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1
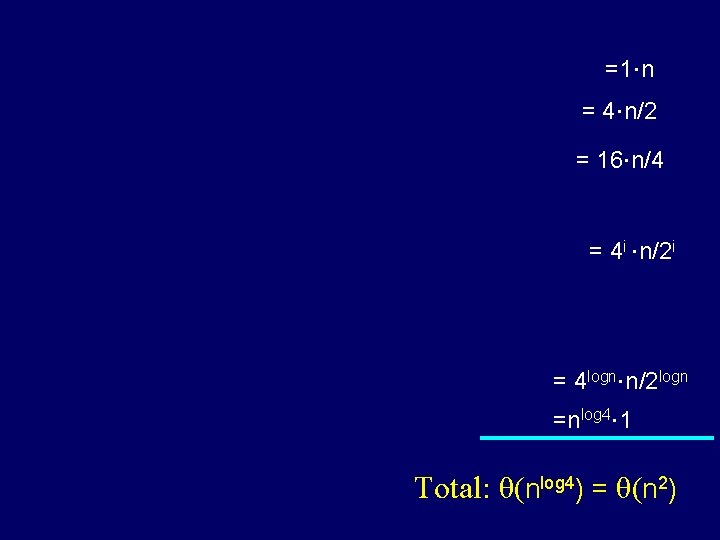
=1×n = 4×n/2 = 16×n/4 = 4 i ×n/2 i = 4 logn×n/2 logn =nlog 4× 1 Total: θ(nlog 4) = θ(n 2)

Divide and Conquer MULT: θ(n 2) time Grade School Multiplication: θ(n 2) time All that work for nothing!

MULT(X, Y): MULT revisited If |X| = |Y| = 1 then RETURN XY Break X into a; b and Y into c; d RETURN MULT(a, c) 2 n + (MULT(a, d) + MULT(b, c)) 2 n/2 + MULT(b, d) • MULT calls itself 4 times. Can you see a way to reduce the number of calls?

Gauss’ Hack: Input: a, b, c, d Output: ac, ad+bc, bd • A 1 = ac • A 3 = bd • m 3 = (a+b)(c+d) = ac + ad + bc + bd • A 2 = m 3 – A 1 - A 3 = ad + bc

MULT(X, Y): Gaussified MULT (Karatsuba 1962) If |X| = |Y| = 1 then RETURN XY Break X into a; b and Y into c; d e = MULT(a, c) and f =MULT(b, d) RETURN e 2 n + (MULT(a+b, c+d) – e - f) 2 n/2 + f • T(n) = 3 T(n/2) + n • Actually: T(n) = 2 T(n/2) + T(n/2 + 1) + kn

T(n) n/2 T(n/4)T(n/4) = n/2 n/2 T(n/4)T(n/4)T(n/4)T(n/4)

T(n) = T(n/2) n T(n/2)

T(n) = n n/2 T(n/4)T(n/4) T(n/2)

T(n) = n n/2 n/2 T(n/4)T(n/4)T(n/4)

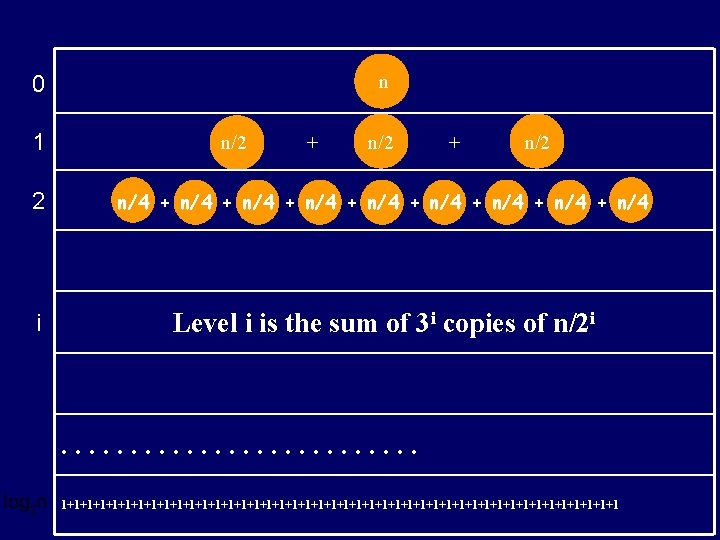
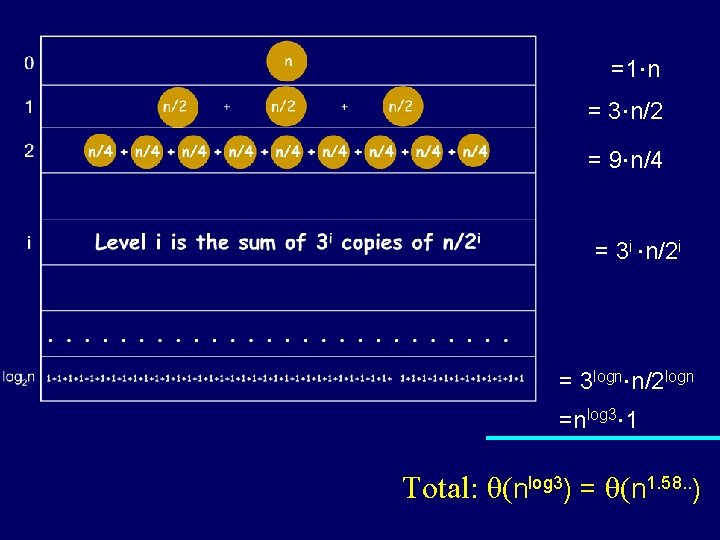
n 0 1 n/2 + n/2 2 n/4 + n/4 + n/4 i Level i is the sum of 3 i copies of n/2 i . . . 1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1

=1×n = 3×n/2 = 9×n/4 = 3 i ×n/2 i = 3 logn×n/2 logn =nlog 3× 1 Total: θ(nlog 3) = θ(n 1. 58. . )

Dramatic improvement for large n Not just a 25% savings! θ( 2 n) vs θ( 1. 58. . n )

Multiplication Algorithms Kindergarten ? Homework 3*4=3+3+3+3 n 2 n Grade School n 2 Karatsuba n 1. 58… Fastest Known n log(n))

You’re cool! Are you free sometime this weekend? Not interested, Bonzo. I took the initiative and asked out a guy in my 4277 class.