Geometric Modeling CSCE 645VIZA 675 Dr Scott Schaefer














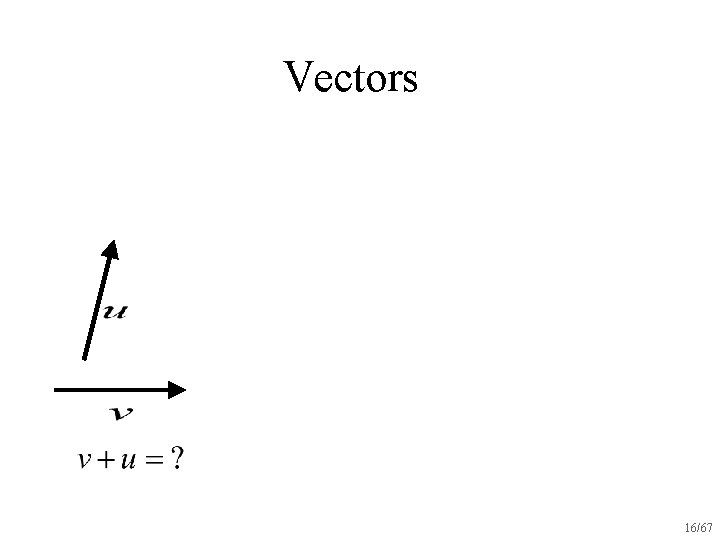
























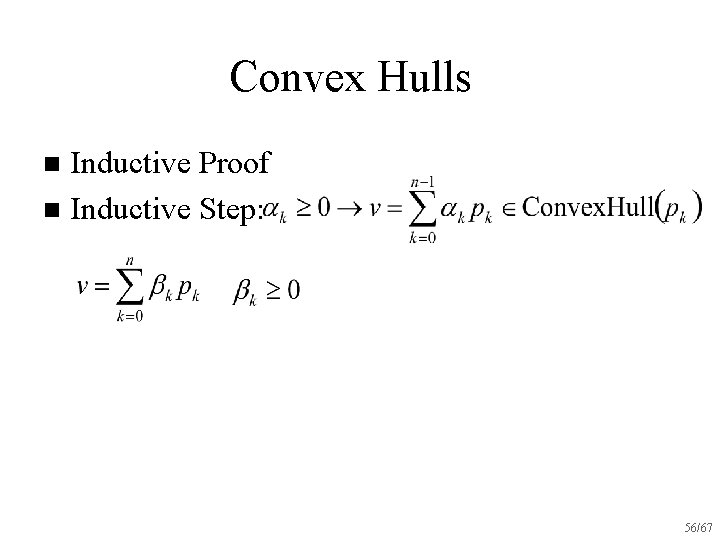
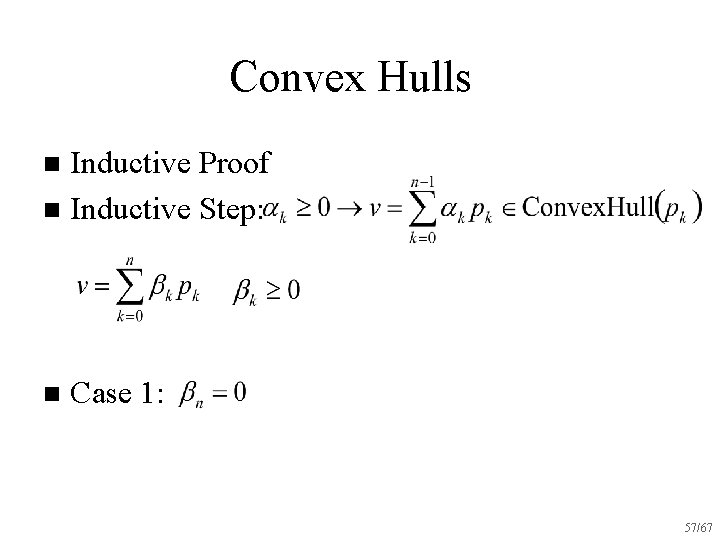

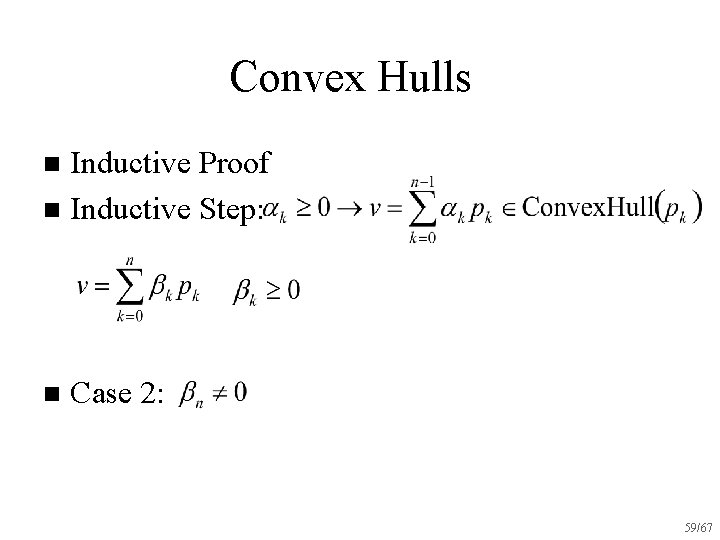
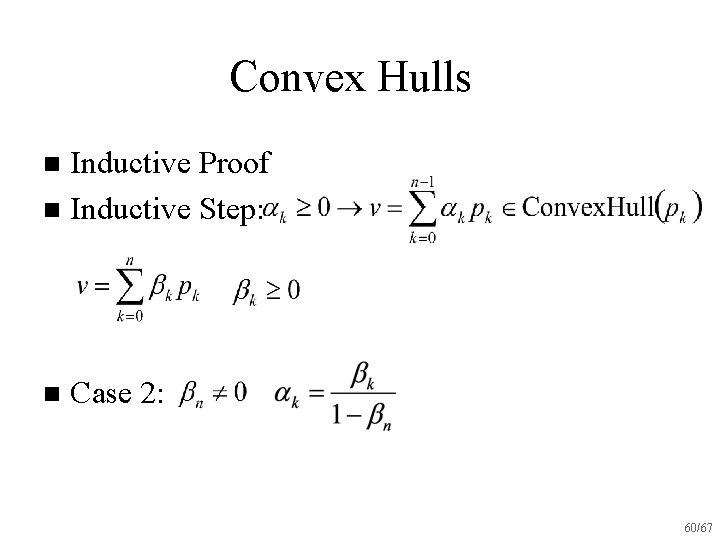
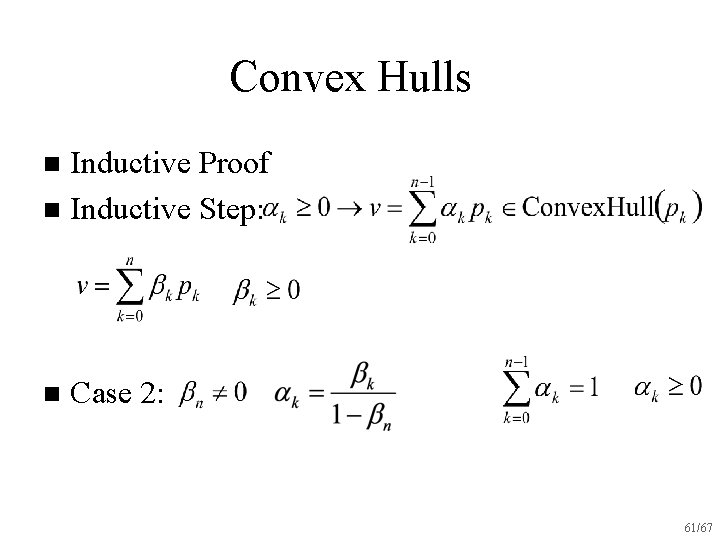
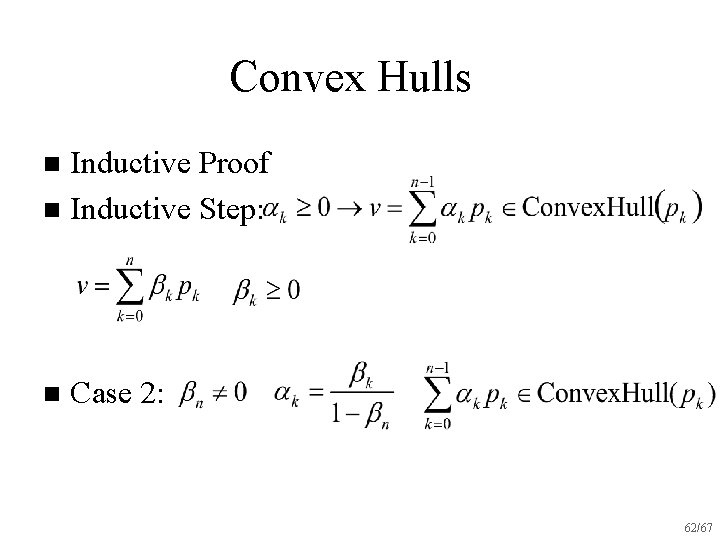
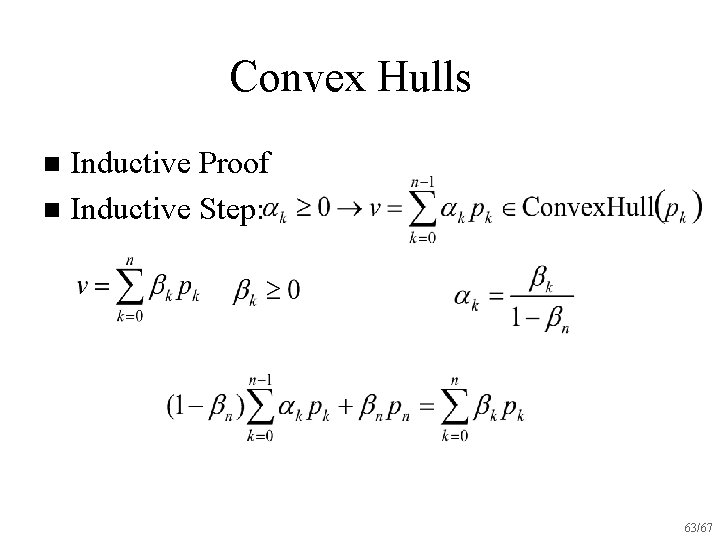
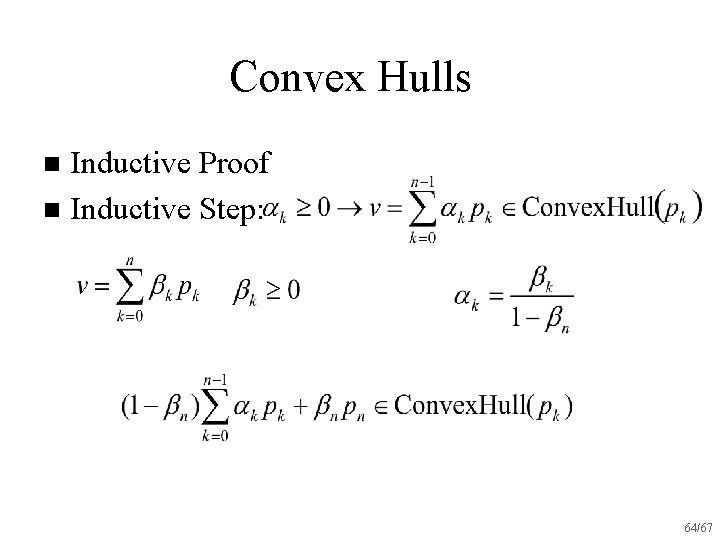



- Slides: 67

Geometric Modeling CSCE 645/VIZA 675 Dr. Scott Schaefer 1

Course Information n Instructor § Dr. Scott Schaefer § HRBB 527 B § Office Hours: TR 10: 00 am – 11: 00 am (or by appointment) n Website: http: //courses. cs. tamu. edu/schaefer/645_Fall 2015 2/67

Geometric Modeling n Surface representations § Industrial design 3/67

Geometric Modeling n Surface representations § Industrial design § Movies and animation 4/67

Geometric Modeling Surface representations § Industrial design § Movies and animation n Surface reconstruction/Visualization n 5/67

Topics Covered n n n n n Polynomial curves and surfaces § Lagrange interpolation § Bezier/B-spline/Catmull-Rom curves § Tensor Product Surfaces § Triangular Patches § Coons/Gregory Patches Differential Geometry Subdivision curves and surfaces Boundary representations Surface Simplification Solid Modeling Free-Form Deformations Barycentric Coordinates Surface Parameterization 6/67

What you’re expected to know n Programming Experience § Assignments in C/C++ n Simple Mathematics Graphics is mathematics made visible 7/67

How much math? n n General geometry/linear algebra Matrices § Multiplication, inversion, determinant, eigenvalues/vectors Vectors § Dot product, cross product, linear independence Proofs § Induction 8/67

Required Textbook 9/67

Grading 60% Homework n 40% Class Project n n No exams! 10/67

Class Project n n Topic: your choice § Integrate with research § Originality Reports § Proposal: 9/22 § Update #1: 10/22 § Update #2: 11/12 § Final report/presentation: 12/8, 12/11 11/67

Class Project Grading 10% Originality n 20% Reports (5% each) n 5% Final Oral Presentation n 65% Quality of Work n http: //courses. cs. tamu. edu/schaefer/645_Fall 2015/assignments/project. html 12/67

Honor Code Your work is your own n You may discuss concepts with others n Do not look at other code. § You may use libraries not related to the main part of the assignment, but clear it with me first just to be safe. n 13/67

Questions? 14/67

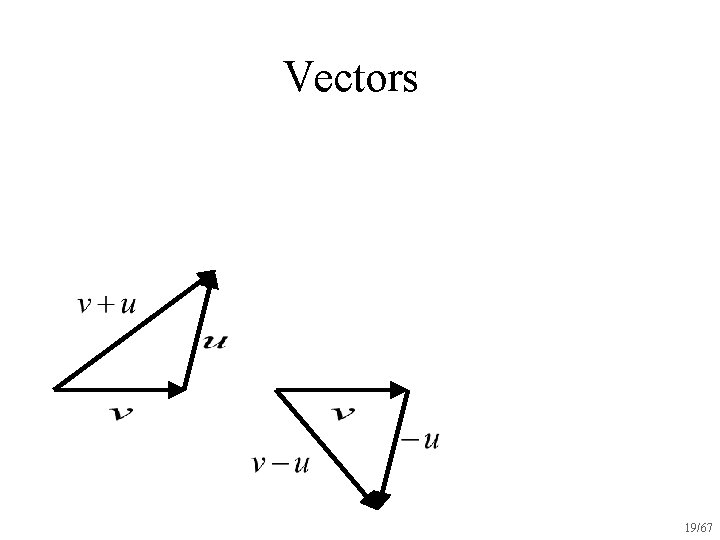
Vectors 15/67
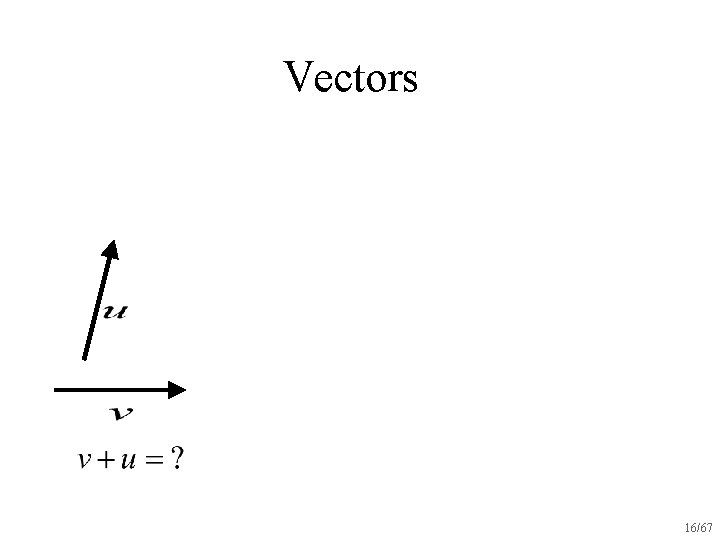
Vectors 16/67

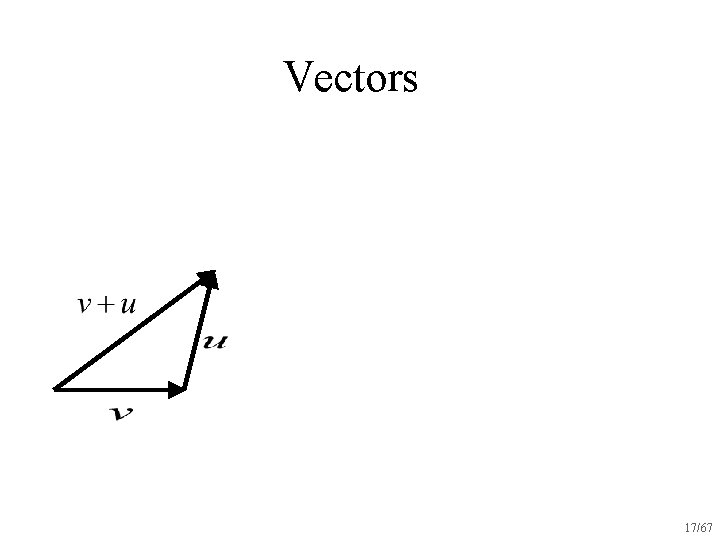
Vectors 17/67

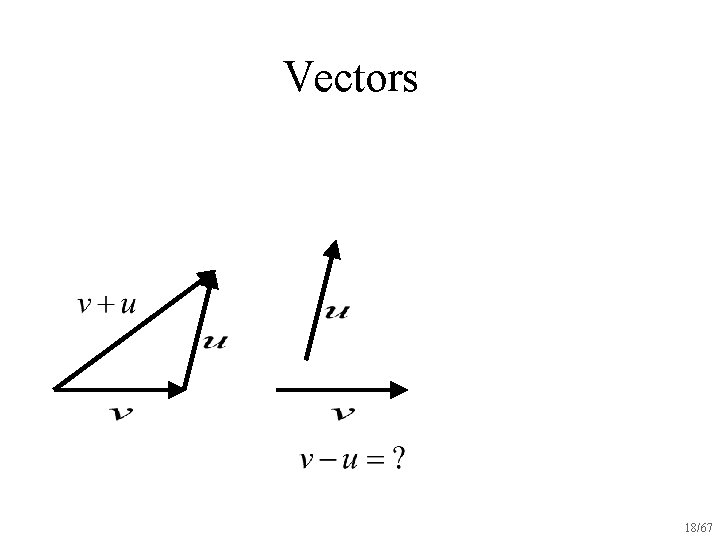
Vectors 18/67

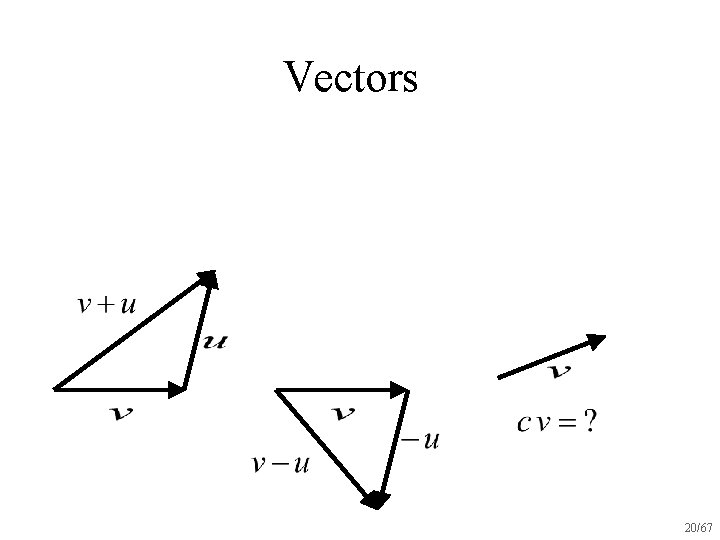
Vectors 19/67

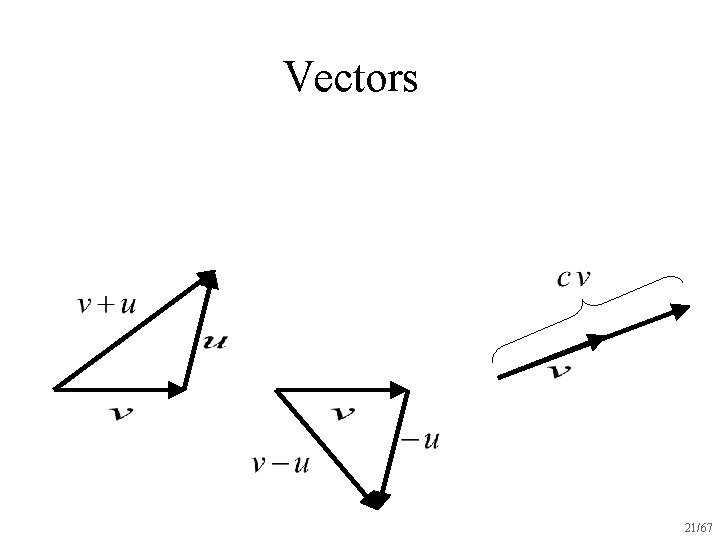
Vectors 20/67

Vectors 21/67

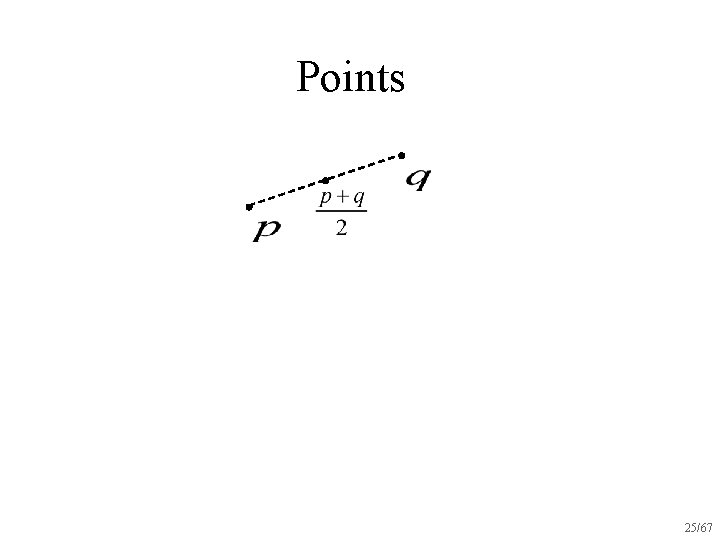
Points 22/67

Points 23/67

Points 24/67

Points 25/67

Points 1 p=p n 0 p=0 (vector) n c p=undefined where c n p – q = v (vector) n 0, 1 26/67

Points 27/67

Points 28/67

Points 29/67

Points 30/67

Points 31/67

Points 32/67

Points 33/67

Points 34/67

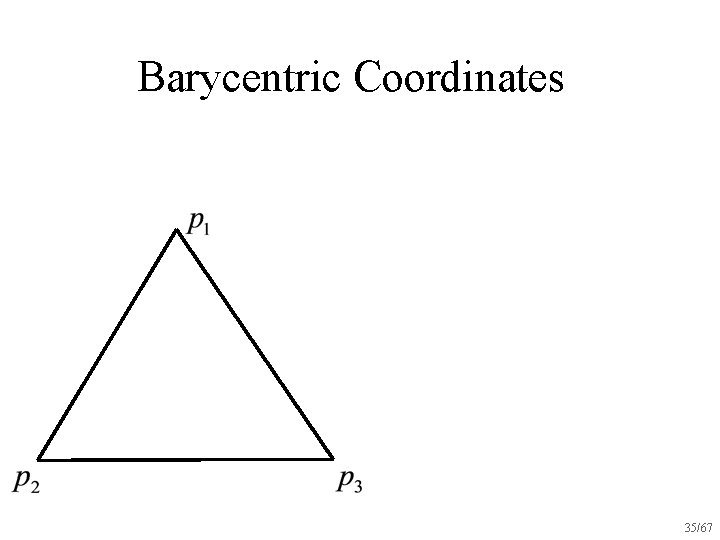
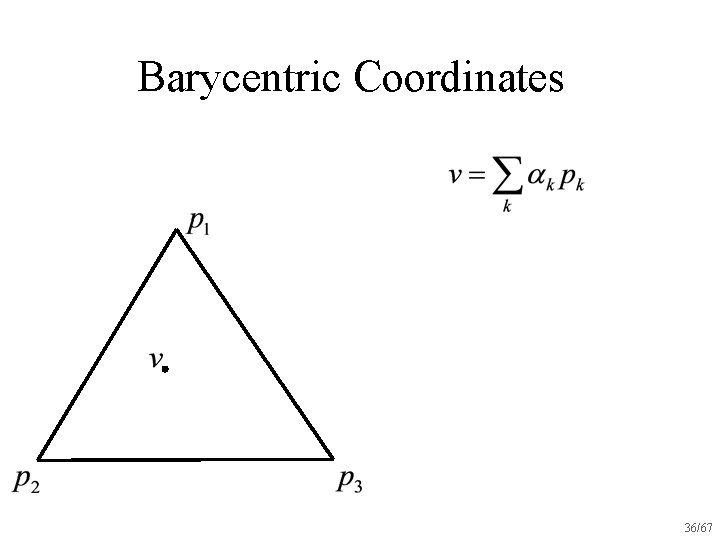
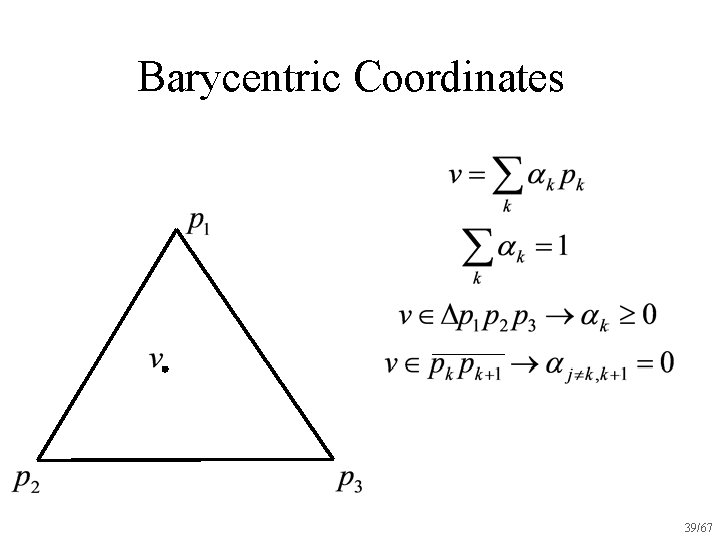
Barycentric Coordinates 35/67

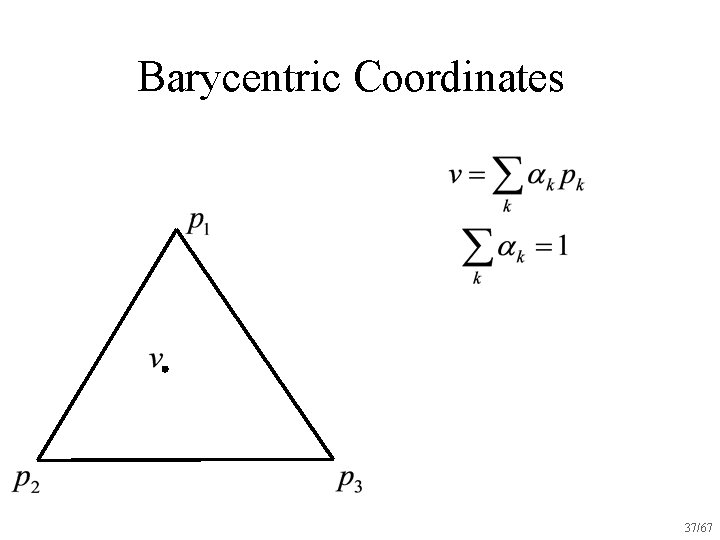
Barycentric Coordinates 36/67

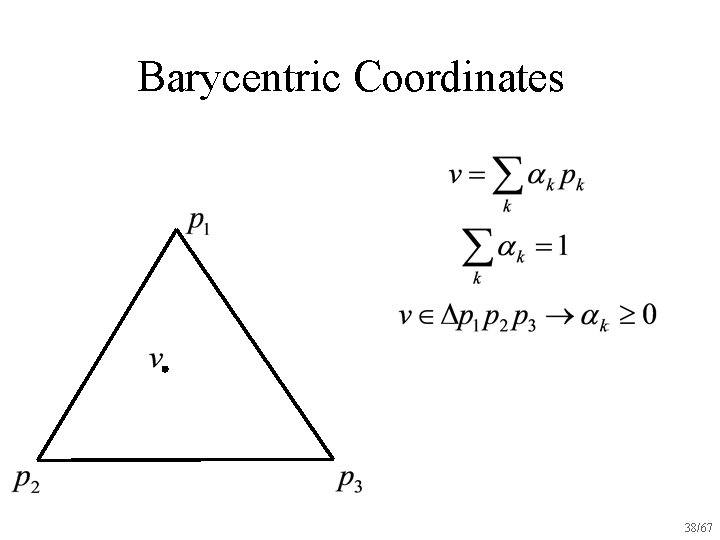
Barycentric Coordinates 37/67

Barycentric Coordinates 38/67

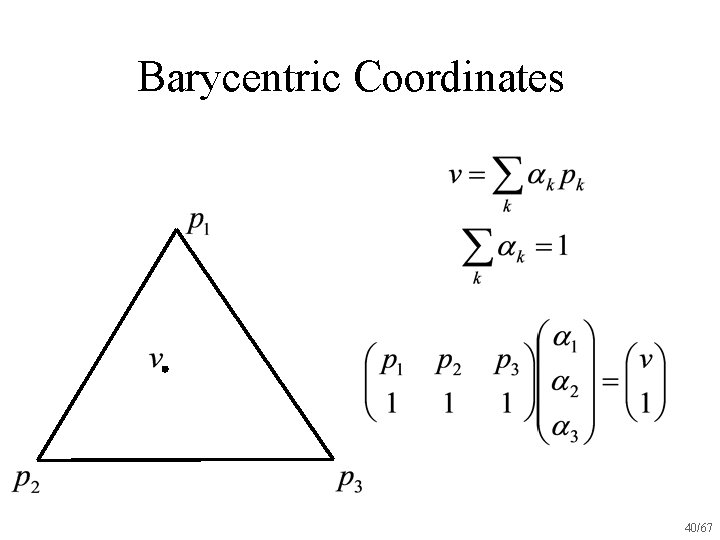
Barycentric Coordinates 39/67

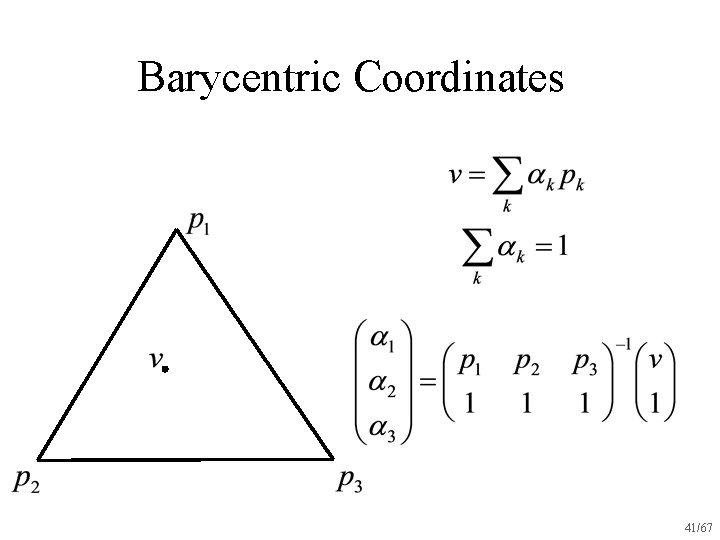
Barycentric Coordinates 40/67

Barycentric Coordinates 41/67

Convex Sets n If , then the combination form a convex 42/67

Convex Hulls n Smallest convex set containing all the 43/67

Convex Hulls n Smallest convex set containing all the 44/67

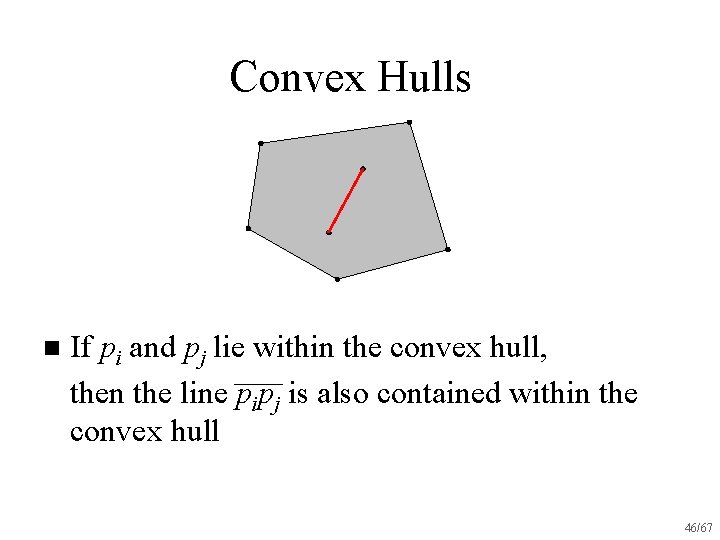
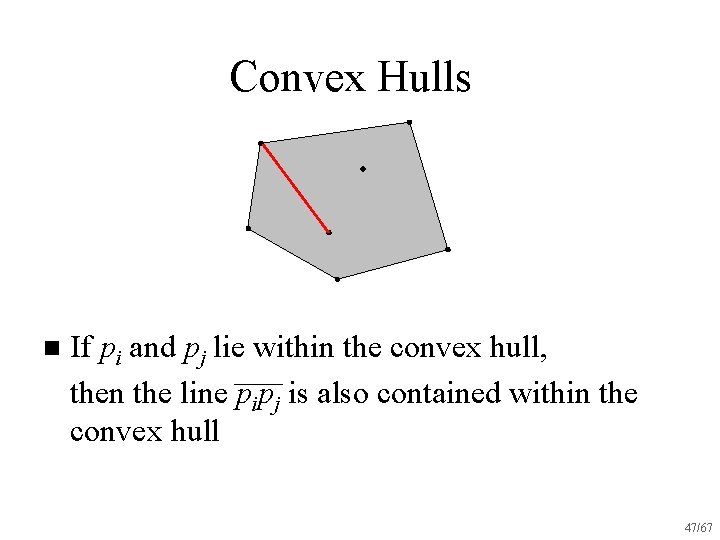
Convex Hulls n If pi and pj lie within the convex hull, then the line pipj is also contained within the convex hull 45/67

Convex Hulls n If pi and pj lie within the convex hull, then the line pipj is also contained within the convex hull 46/67

Convex Hulls n If pi and pj lie within the convex hull, then the line pipj is also contained within the convex hull 47/67

Convex Hulls n If pi and pj lie within the convex hull, then the line pipj is also contained within the convex hull 48/67

Convex Hulls n If pi and pj lie within the convex hull, then the line pipj is also contained within the convex hull 49/67

Convex Hulls n If pi and pj lie within the convex hull, then the line pipj is also contained within the convex hull 50/67

Convex Hulls n If pi and pj lie within the convex hull, then the line pipj is also contained within the convex hull 51/67

Convex Hulls n If pi and pj lie within the convex hull, then the line pipj is also contained within the convex hull 52/67

Convex Hulls n If pi and pj lie within the convex hull, then the line segment pipj is also contained within the convex hull 53/67

Convex Hulls Inductive Proof n Base Case: 1 point p 0 is its own convex hull n 54/67

Convex Hulls Inductive Proof n Inductive Step: n 55/67
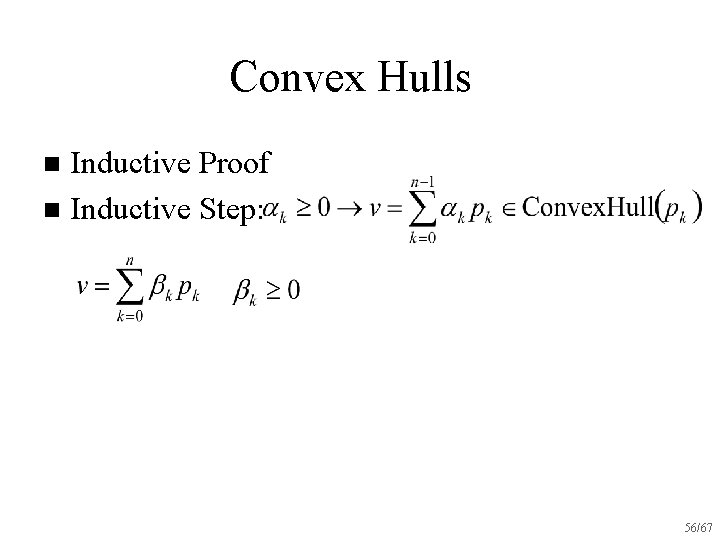
Convex Hulls Inductive Proof n Inductive Step: n 56/67
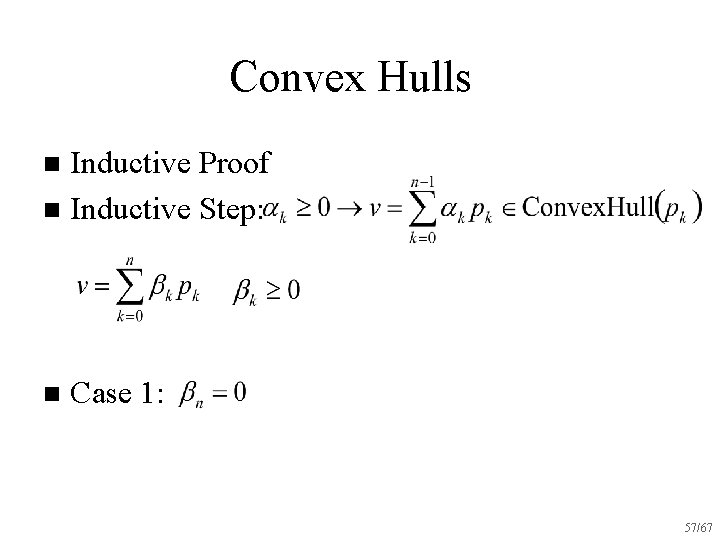
Convex Hulls Inductive Proof n Inductive Step: n n Case 1: 57/67

Convex Hulls Inductive Proof n Inductive Step: n n Case 1: 58/67
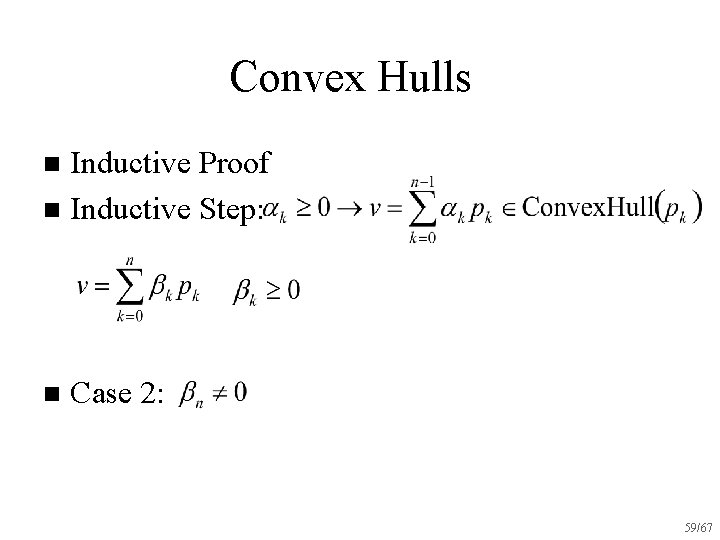
Convex Hulls Inductive Proof n Inductive Step: n n Case 2: 59/67
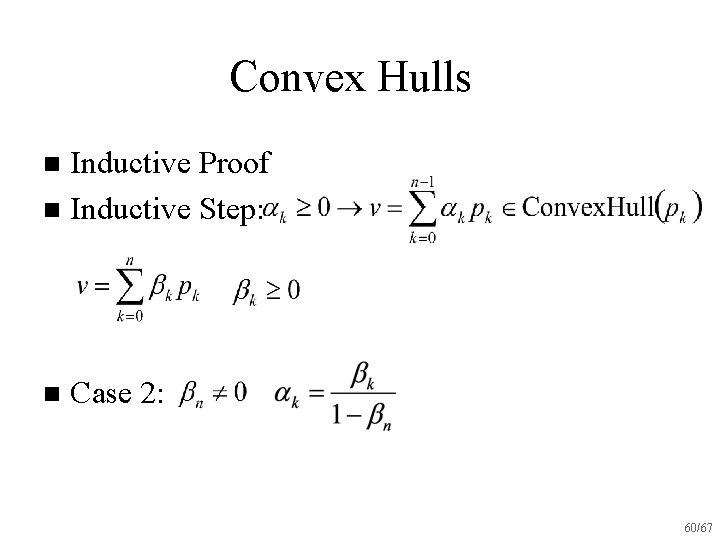
Convex Hulls Inductive Proof n Inductive Step: n n Case 2: 60/67
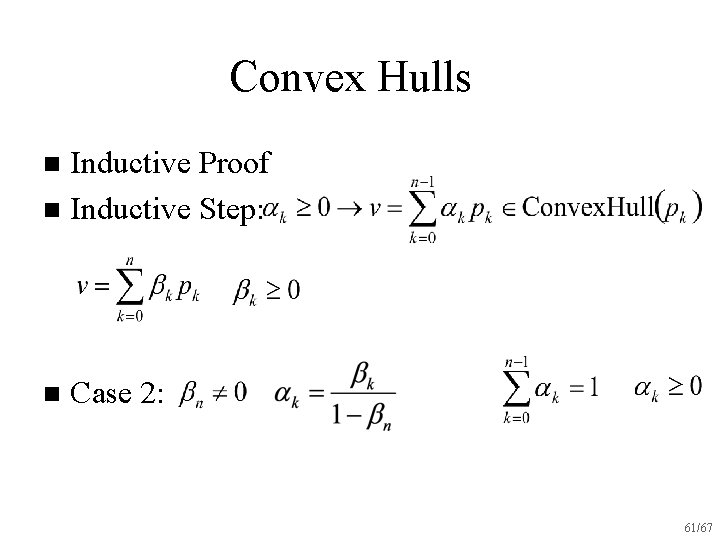
Convex Hulls Inductive Proof n Inductive Step: n n Case 2: 61/67
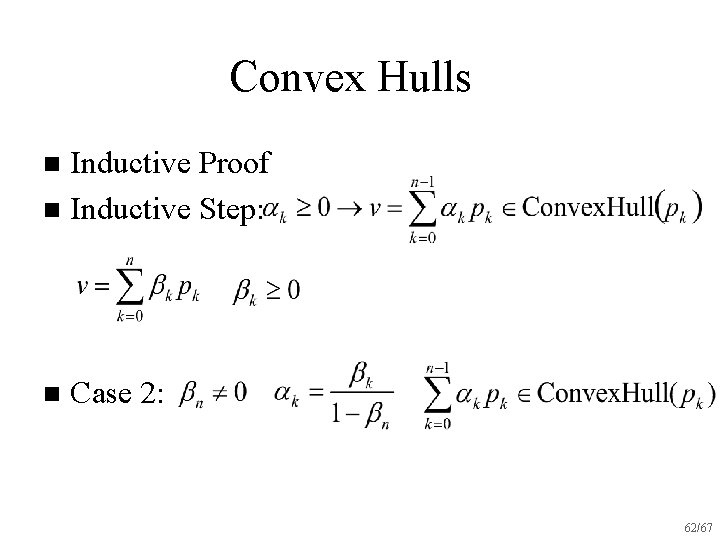
Convex Hulls Inductive Proof n Inductive Step: n n Case 2: 62/67
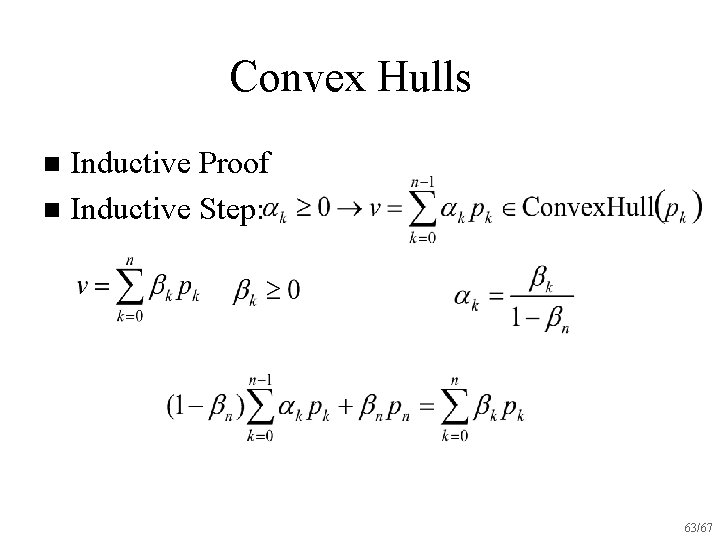
Convex Hulls Inductive Proof n Inductive Step: n 63/67
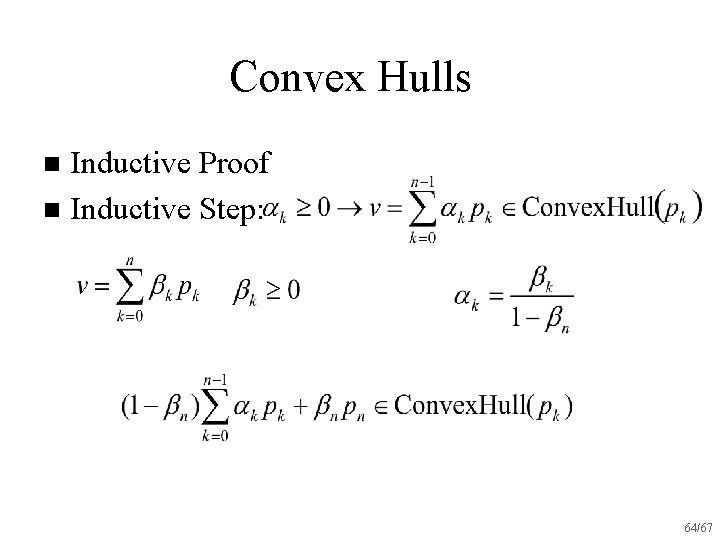
Convex Hulls Inductive Proof n Inductive Step: n 64/67

Affine Transformations n Preserve barycentric combinations n Examples: translation, rotation, uniform scaling, non-uniform scaling, shear 65/67

Other Transformations Conformal § Preserve angles under transformation § Examples: translation, rotation, uniform scaling n Rigid § Preserve angles and length under transformation § Examples: translation, rotation n 66/67

Vector Spaces n A set of vectors vk are independent if n The span of a set of vectors vk is n A basis of a vector space is a set of independent vectors vk such that 67/67