Geometric Construction Notes Click on the title to

Geometric Construction Notes Click on the title to view a tutorial

Table of Contents How to navigate this presentation Geometric Construction Introduction Drawing Guidelines Parts of the Safe-T Compass How to Use the Safe-T Compass Draw a Perpendicular Bisector to a Line Bisect an Arc Bisect an Angle Transfer an Angle Construct a Triangle From 3 Sides Construct a Equilateral Triangle

How to Navigate This Presentation This presentation is designed to be completely self guided and interactive. Here a few guidelines to help you navigate this presentation: Clicking on the slide or using the right or down arrow keys will take you to the next slide Using the left or up arrow keys will take you to the previous slide

Symbols Underlined Blue Text will take you to a) the corresponding page from the table of contents b) the web source from the Works Cited Page The book will take you back to the Table of Contents The blue numbers in the slide contents will link you to the corresponding Works Cited Page with the Source Information The Bald Eagle will take you back to the beginning of the topic #

Geometric Construction Introduction • Based on principles of pure geometry and may be applied to any shape regardless of the size. • CAD is based on geometric construction so understanding geometric construction makes understanding how CAD tools work easier and increases proficiency.

Background- Euclidian Geometry was developed by a Roman citizen named Euclid lived from approx. 330 to 260 bc and wrote a 13 volume book called Elements which illustrated all the concepts used in Geometric Construction

Background- Why Didn’t He Just Use a Ruler The Greeks could not do arithmetic because: 1. They had only positive whole numbers represented by Roman numerals (I, III, IV, V) - no negative numbers - no fractions or decimals -no zero

Background- Why Didn’t He Just Use a Ruler So if the line were any length other than an even answer it could not be solved in Roman culture. Example: 5 / 2= 2. 5 2. Had no measurement system with units so a line could not be measured. As a result they had to use other tools such as a compass and straight edge.

Drawing Guidelines • Draw constructions very lightly using guidelines. • Do NOT erase your guidelines- show your work. • Only trace over the final solution NOT the construction.

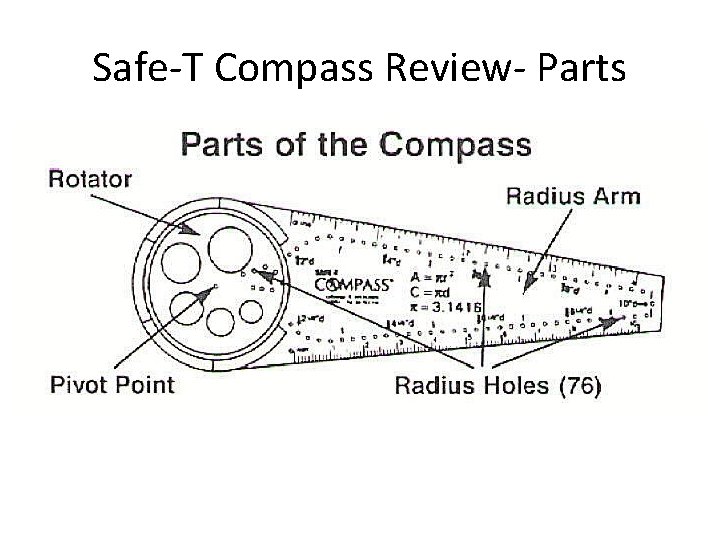
Safe-T Compass Review- Parts

Safe-T Compass Review- Procedure 1. Place the pivot point of the Safe. T compass on the CP of the arc you want to draw. 2. Hold the rotator in place with your non-dominate hand. 3. Put the point of your pencil in an appropriate radius hole 4. Rotate the radius arm around the rotator by dragging your pencil.

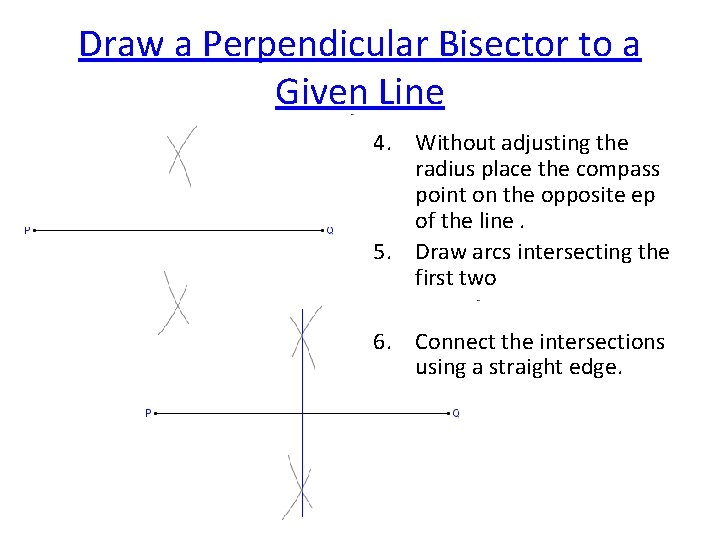
Draw a Perpendicular Bisector to a Given Line Begin with a given line 1. Place the compass point on one end point (ep) of the line. 2. Adjust the compass radius to approximately 2/3 the length of the line (radius must be > ½ the length of the line but actual size does not matter) 3. Draw an arc above and below the line.

Draw a Perpendicular Bisector to a Given Line 4. Without adjusting the radius place the compass point on the opposite ep of the line. 5. Draw arcs intersecting the first two 6. Connect the intersections using a straight edge.

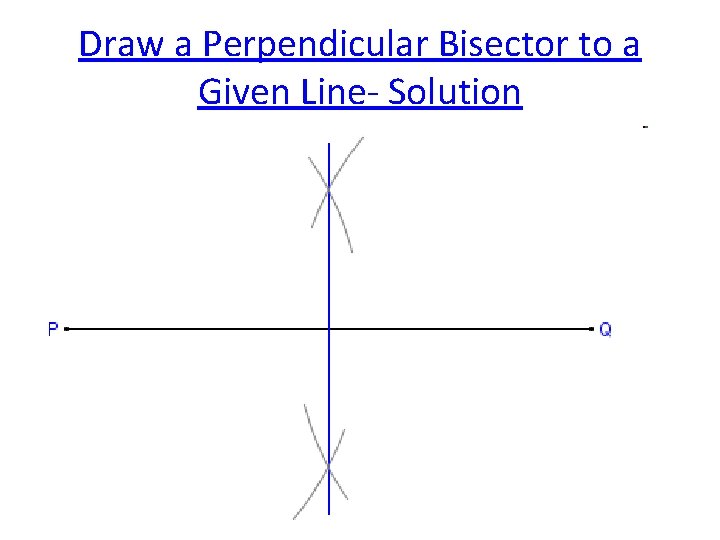
Draw a Perpendicular Bisector to a Given Line- Solution

Summarize the Steps in Your Own Words

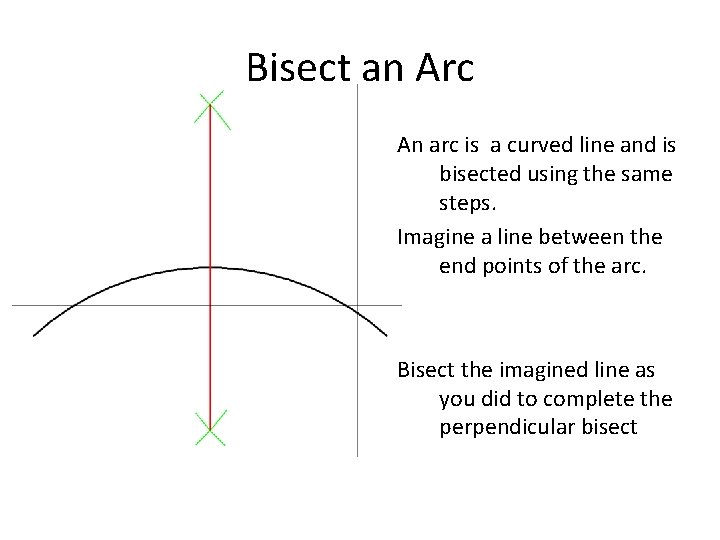
Bisect an Arc An arc is a curved line and is bisected using the same steps. Imagine a line between the end points of the arc. Bisect the imagined line as you did to complete the perpendicular bisect

Summarize the Steps in Your Own Words

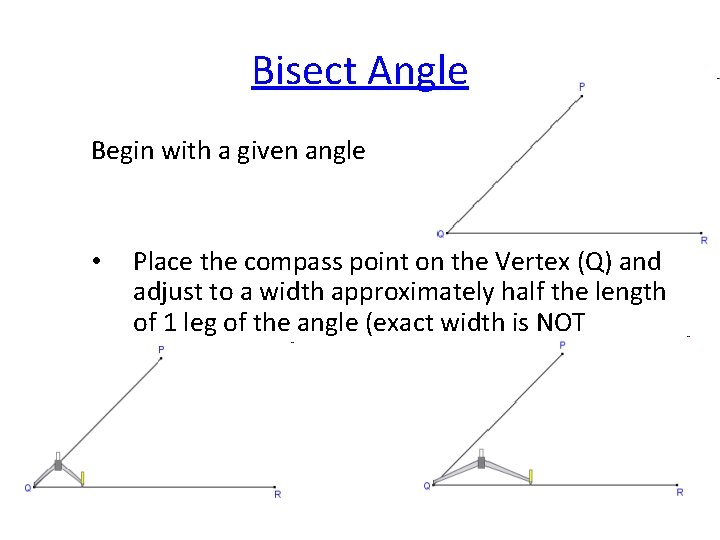
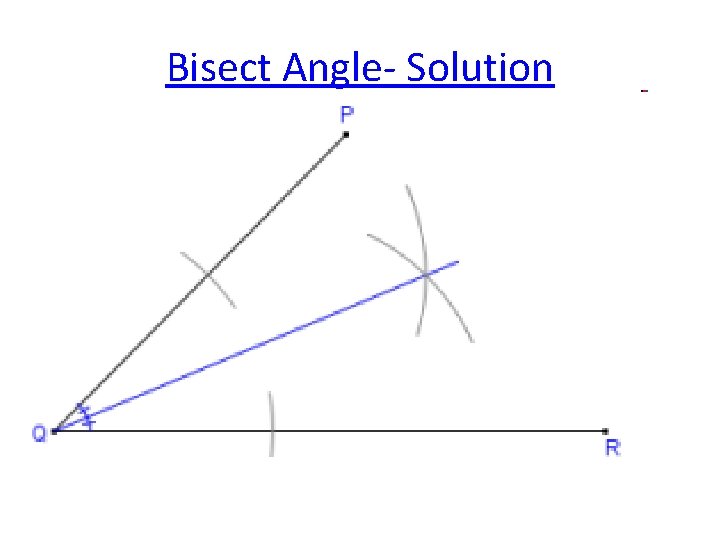
Bisect Angle Begin with a given angle • Place the compass point on the Vertex (Q) and adjust to a width approximately half the length of 1 leg of the angle (exact width is NOT important)

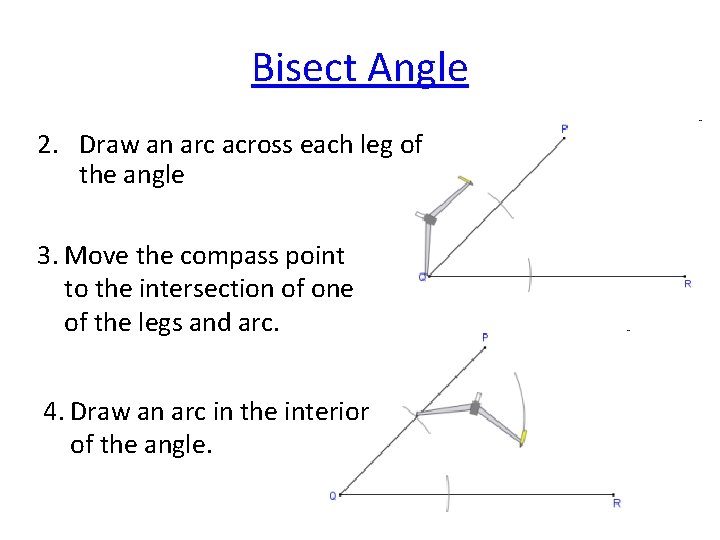
Bisect Angle 2. Draw an arc across each leg of the angle 3. Move the compass point to the intersection of one of the legs and arc. 4. Draw an arc in the interior of the angle.

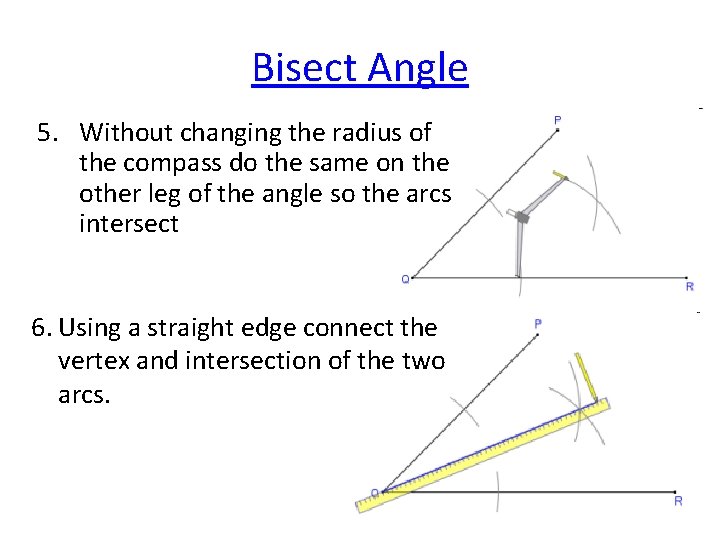
Bisect Angle 5. Without changing the radius of the compass do the same on the other leg of the angle so the arcs intersect 6. Using a straight edge connect the vertex and intersection of the two arcs.

Bisect Angle- Solution

Summarize the Steps in Your Own Words

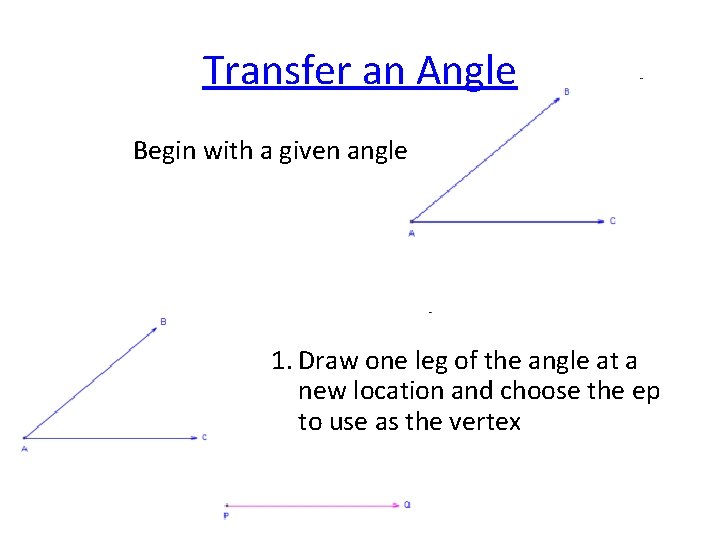
Transfer an Angle Begin with a given angle 1. Draw one leg of the angle at a new location and choose the ep to use as the vertex

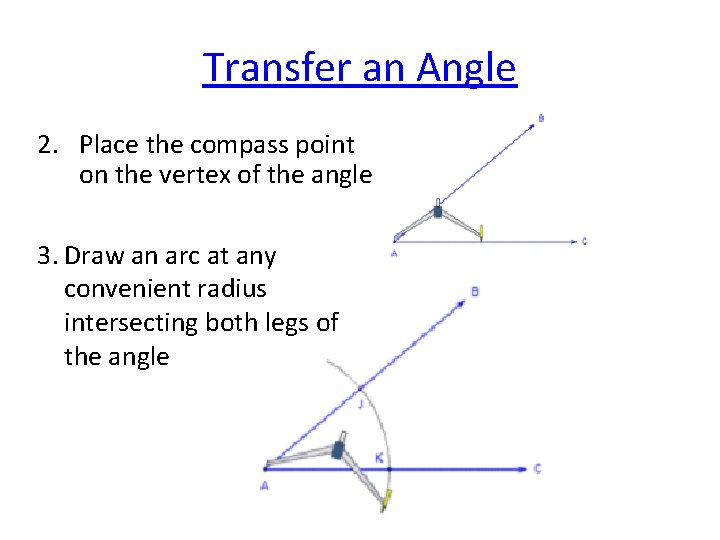
Transfer an Angle 2. Place the compass point on the vertex of the angle 3. Draw an arc at any convenient radius intersecting both legs of the angle

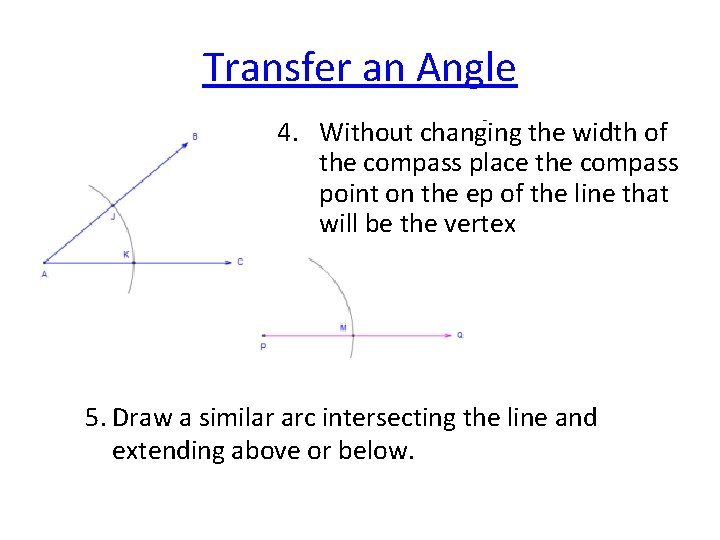
Transfer an Angle 4. Without changing the width of the compass place the compass point on the ep of the line that will be the vertex 5. Draw a similar arc intersecting the line and extending above or below.

Transfer an Angle 6. Place the point of the compass on the intersection of the arc and one of the legs 7. Adjust the compass so the lead is on the other intersection of the arc and opposite leg.

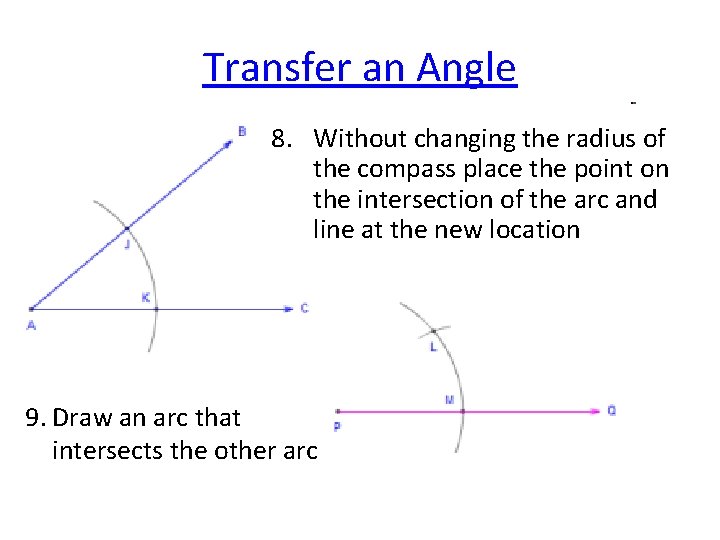
Transfer an Angle 8. Without changing the radius of the compass place the point on the intersection of the arc and line at the new location 9. Draw an arc that intersects the other arc

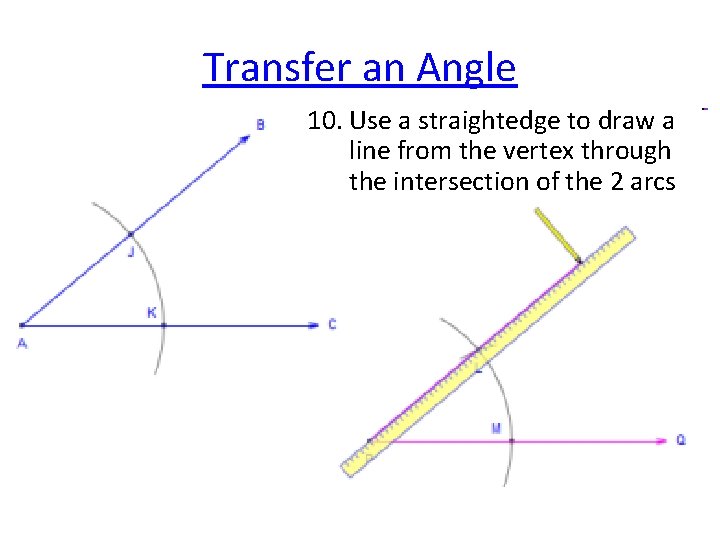
Transfer an Angle 10. Use a straightedge to draw a line from the vertex through the intersection of the 2 arcs

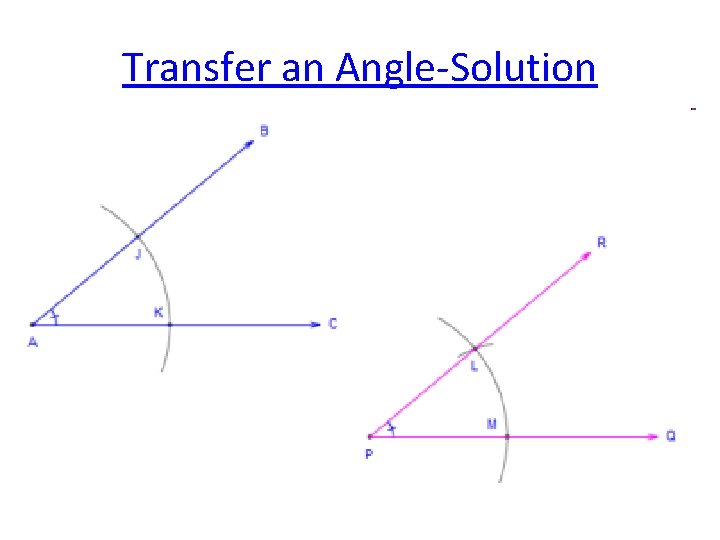
Transfer an Angle-Solution

Summarize the Steps in Your Own Words

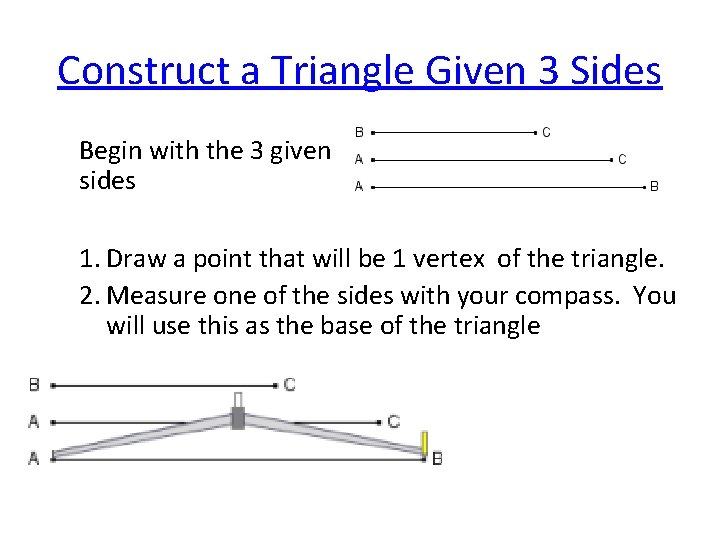
Construct a Triangle Given 3 Sides Begin with the 3 given sides 1. Draw a point that will be 1 vertex of the triangle. 2. Measure one of the sides with your compass. You will use this as the base of the triangle

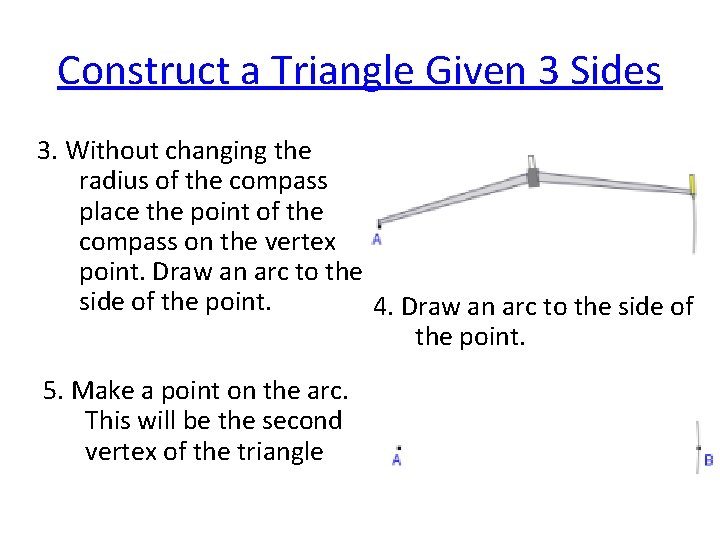
Construct a Triangle Given 3 Sides 3. Without changing the radius of the compass place the point of the compass on the vertex point. Draw an arc to the side of the point. 4. Draw an arc to the side of the point. 5. Make a point on the arc. This will be the second vertex of the triangle

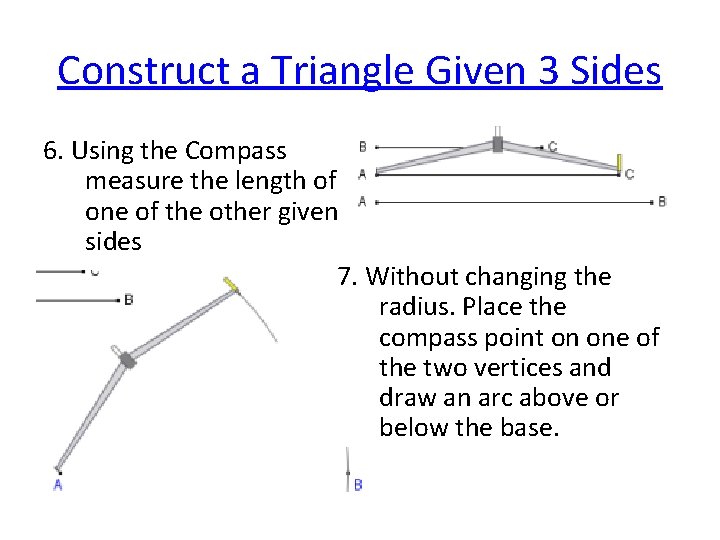
Construct a Triangle Given 3 Sides 6. Using the Compass measure the length of one of the other given sides 7. Without changing the radius. Place the compass point on one of the two vertices and draw an arc above or below the base.

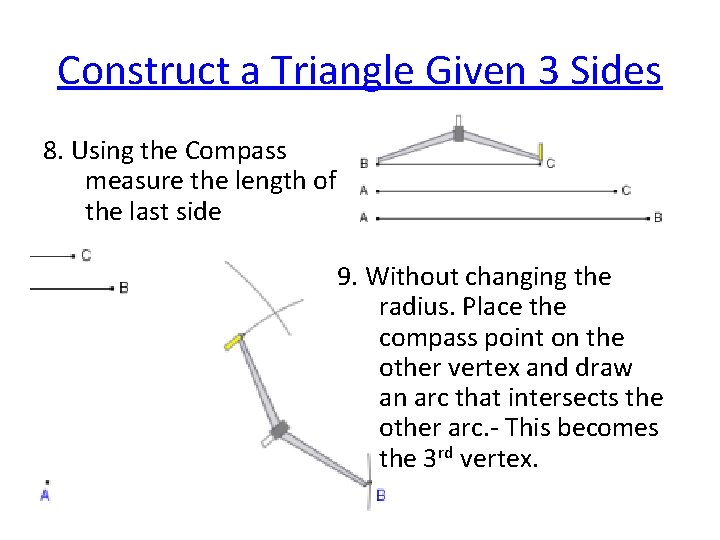
Construct a Triangle Given 3 Sides 8. Using the Compass measure the length of the last side 9. Without changing the radius. Place the compass point on the other vertex and draw an arc that intersects the other arc. - This becomes the 3 rd vertex.

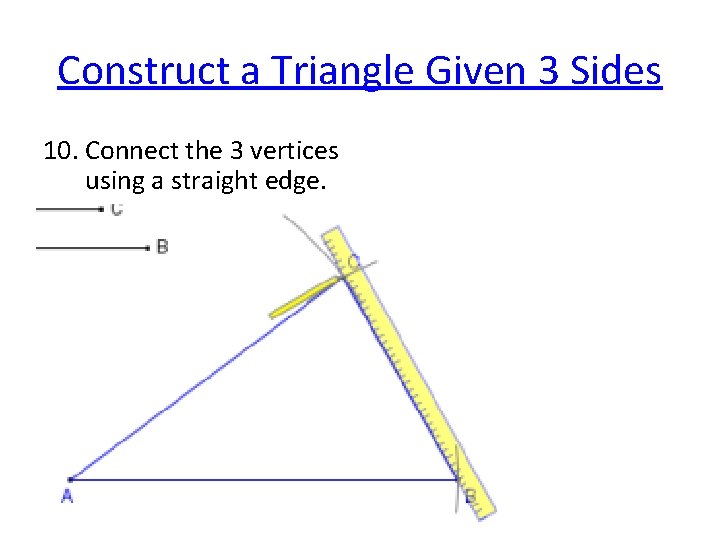
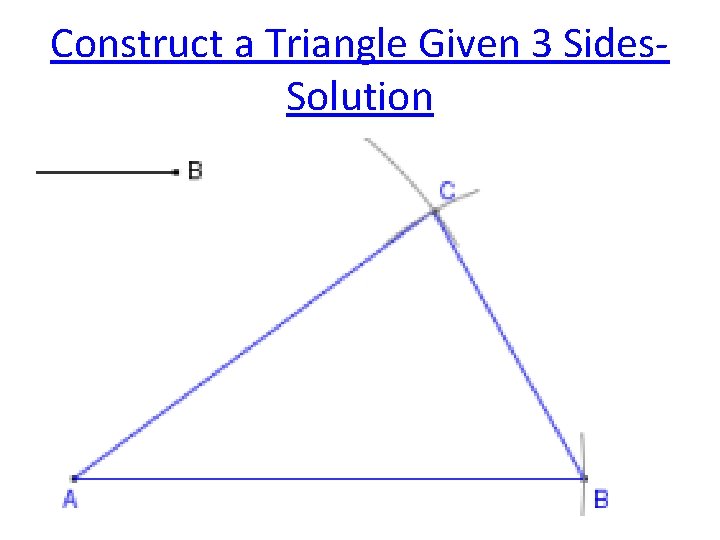
Construct a Triangle Given 3 Sides 10. Connect the 3 vertices using a straight edge.

Construct a Triangle Given 3 Sides. Solution

Summarize the Steps in Your Own Words

Construct an Equilateral Triangle Given 1 Side 1. Begin by Making a point. This will be the first vertex 2. Using the compass measure the length of the given side and set the compass point on your first vertex. 3. Draw arcs to the side of the first vertex where you want the 2 nd vertex and an arc above or below to locate the 3 rd vertex

Construct an Equilateral Triangle Given 1 Side 4. Place a point on one of the two arcs- This will be the second vertex 5. Without adjusting the radius of the compass place the point on the second vertex point and draw an arc intersecting the first arc.

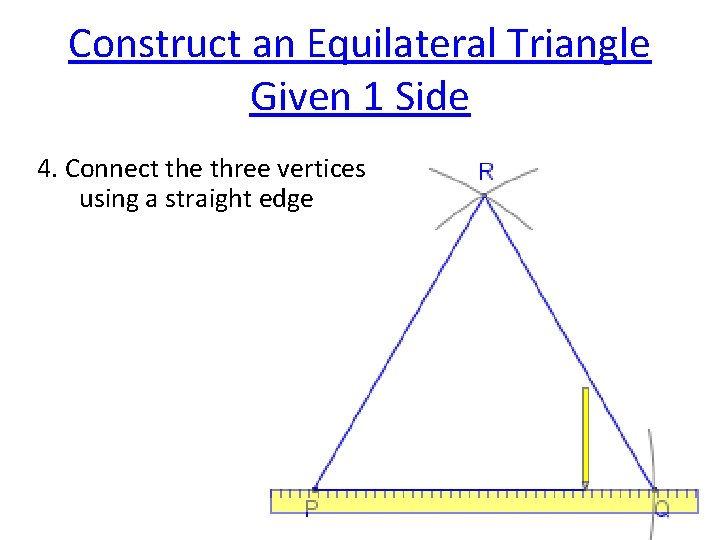
Construct an Equilateral Triangle Given 1 Side 4. Connect the three vertices using a straight edge

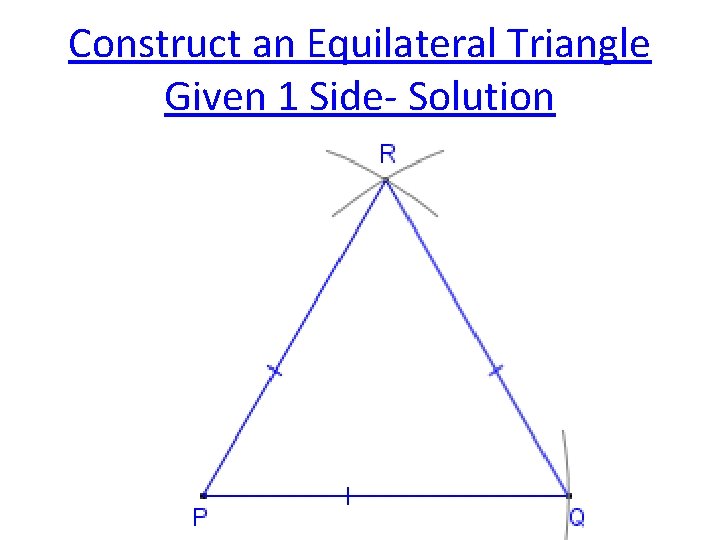
Construct an Equilateral Triangle Given 1 Side- Solution

Summarize the Steps in Your Own Words

Summary Identify how the exercises relate to one another: - What do you learn from bisecting a line that you can apply to bisecting an arc? - How do you use what you learned from bisecting an arc to bisect an angle - How do the skills learned from bisecting an angle help you to transfer an angle?