NOTES GEOMETRIC MEAN SIMILARITY IN RIGHT TRIANGLES I

Simplifying Radicals Perfect Squares – 1, 4, 9, 16, 25, 36, 49, 64, 81…

What if you picked 9 instead of 36? If you pick a smaller Perfect

Geometric Mean is the square root of the product of two values. If a,

Similarity in Right Triangles Altitude – segment drawn from 90 degrees to the opposite

Right Triangle Similarity Theorem - If the altitude is drawn to the hypotenuse of

Similarity in Right Triangles - Corollary 1 alt seg 1 seg 2 The length

Example Find the length of the altitude. 3 x X 3 6 = 18

Similarity in Right Triangles – Corollary 2 leg SHAL hypotenuse Each leg of the

Example 3 Find the length of the leg. y 5+2 = y 2 7

Similarity in Right Triangles Solve for x. 2 = 6 6 x 2 x

Similarity in Right Triangles Solve for y. x y = y 2+x Write a

Slides: 12

Download presentation

NOTES GEOMETRIC MEAN / SIMILARITY IN RIGHT TRIANGLES I can use relationships in similar right triangles.

Simplifying Radicals Perfect Squares – 1, 4, 9, 16, 25, 36, 49, 64, 81… Find the largest Perfect Square that goes into the number evenly example: 72 The largest Perfect Square that goes into 72 is 36. = 36 x 2 =6 2

What if you picked 9 instead of 36? If you pick a smaller Perfect Square you must reduce more than once. example: 72 9 is a Perfect Square that goes into 72 evenly, though not the largest = = = 9 x 8 3 8 8 can be divided by another Perfect Square, 4 3 4 x 2 3 x 2 2 6 2

Geometric Mean is the square root of the product of two values. If a, b, and x are positive numbers and geometric mean between a and b. , then x is called the Example : Find the geometric mean of 3 and 12. 3 = x x 12 Write a proportion. x 2 = 36 Cross-Product Property x 2 = 36 Find the positive square root. x=6 The geometric mean of 3 and 12 is 6.

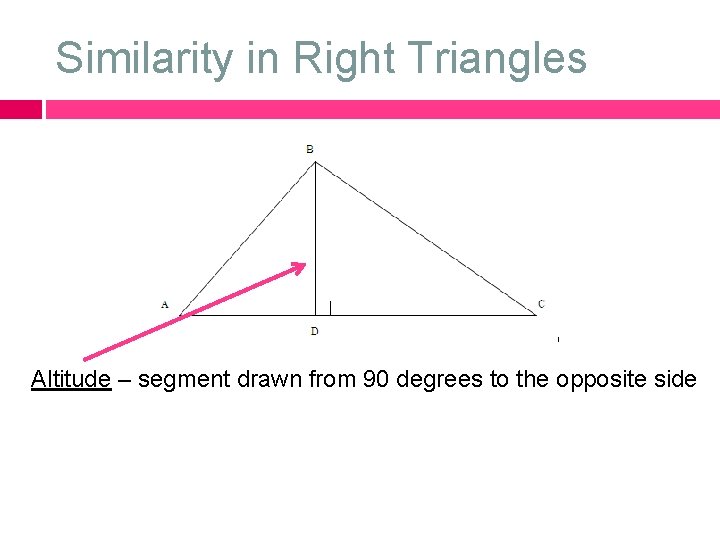
Similarity in Right Triangles Altitude – segment drawn from 90 degrees to the opposite side

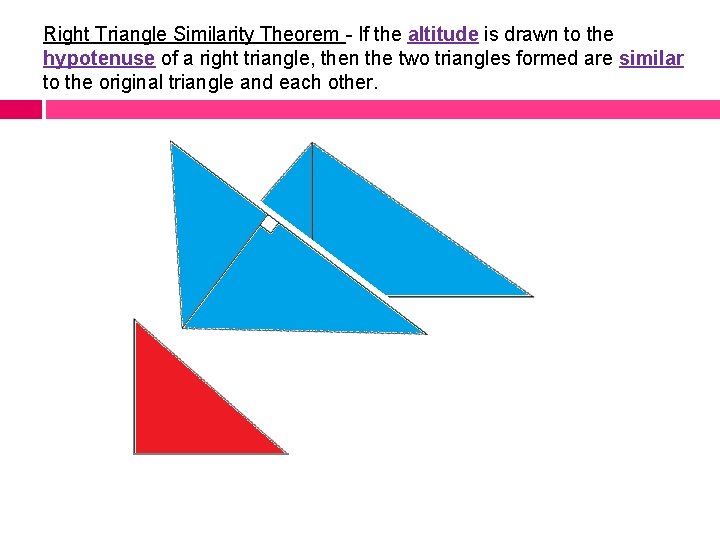
Right Triangle Similarity Theorem - If the altitude is drawn to the hypotenuse of a right triangle, then the two triangles formed are similar to the original triangle and each other.

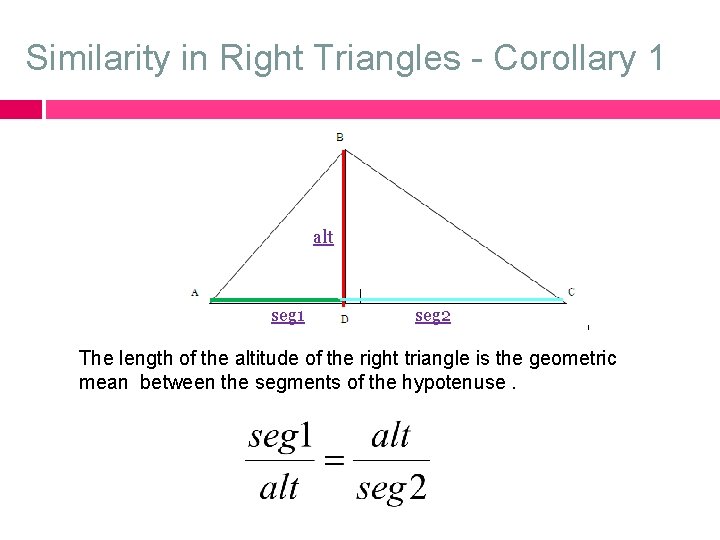
Similarity in Right Triangles - Corollary 1 alt seg 1 seg 2 The length of the altitude of the right triangle is the geometric mean between the segments of the hypotenuse.

Example Find the length of the altitude. 3 x X 3 6 = 18 = x 2 √ 18 = x √ 9 ∙ √ 2 = x 3 √ 2 = x x 6

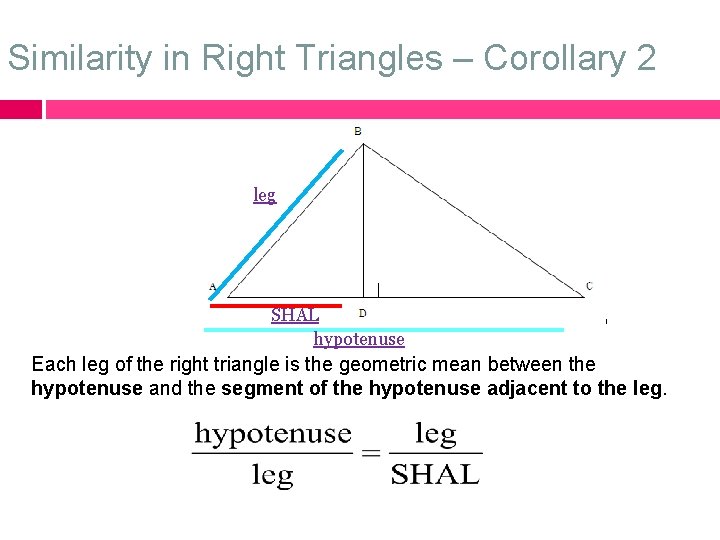
Similarity in Right Triangles – Corollary 2 leg SHAL hypotenuse Each leg of the right triangle is the geometric mean between the hypotenuse and the segment of the hypotenuse adjacent to the leg.

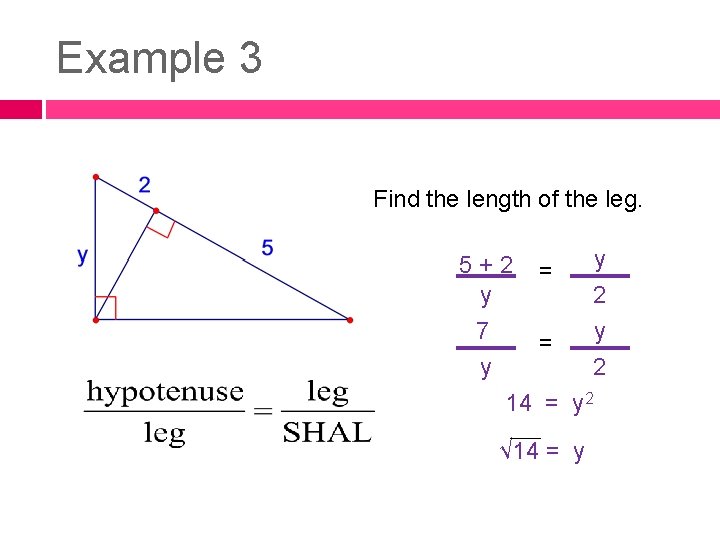
Example 3 Find the length of the leg. y 5+2 = y 2 7 y = y 2 14 = y 2 √ 14 = y

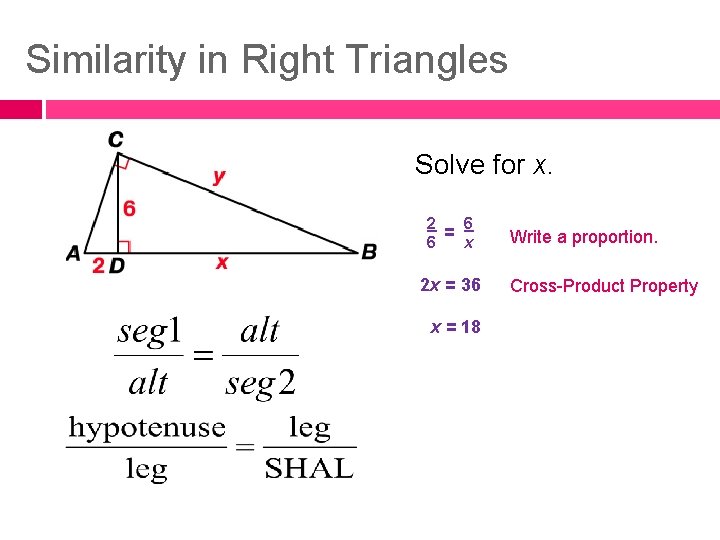
Similarity in Right Triangles Solve for x. 2 = 6 6 x 2 x = 36 x = 18 Write a proportion. Cross-Product Property

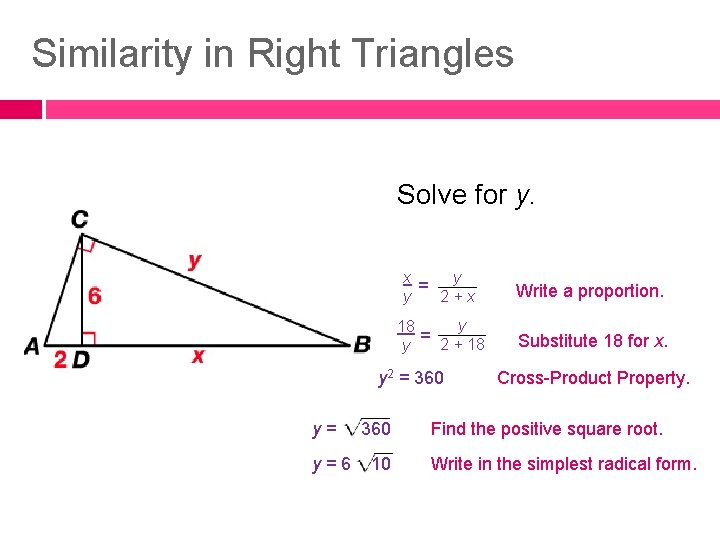
Similarity in Right Triangles Solve for y. x y = y 2+x Write a proportion. y 18 = 2 + 18 y Substitute 18 for x. y 2 = 360 y= y=6 360 10 Cross-Product Property. Find the positive square root. Write in the simplest radical form.