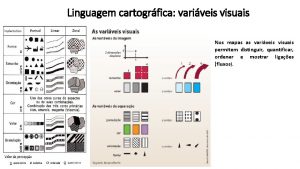
Geoestatstica para geoprocessamento realidade Palavraschave variveis regionalizadas semivariograma

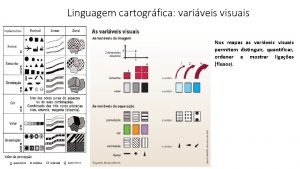
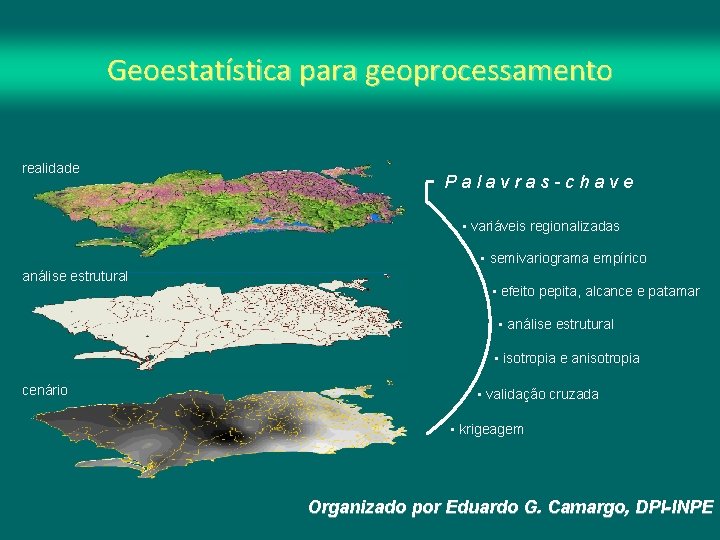
Geoestatística para geoprocessamento realidade Palavras-chave • variáveis regionalizadas • semivariograma empírico análise estrutural • efeito pepita, alcance e patamar • análise estrutural • isotropia e anisotropia cenário • validação cruzada • krigeagem Organizado por Eduardo G. Camargo, DPI-INPE

OBJETIVO Apresentar as principais noções básicas de geoestatística para o tratamento de dados geográficos, com exemplos práticos no sistema Sistema de Processamento de Informações Georeferenciadas - SPRING. 12/4/2020 2

TÓPICOS 12/4/2020 1) Introdução / Motivação 2) Principais conceitos teóricos 3) A função variograma 4) Modelos teóricos de variograma 5) Isotropia e anisotropia 6) Validação cruzada 7) Krigeagem linear 8) Integração: SPRING e geoestatística 3

Parte 1 Introdução / Motivação Origem da geoestatística • Os métodos geoestatísticos, ou simplesmente geoestatística, foram desenvolvidos graças aos estudos do engenheiro de minas Georges Matheron na França no início dos anos 60. • A geoestatística está fundamentada na Teoria das Variáveis Regionalizadas, a qual foi formalizada por Matheron a partir de estudos práticos desenvolvidos por Daniel G. Krige, no cálculo de reservas nas minas de ouro na África do Sul. • Atualmente a geoestatística é aplicada em vários campos, desde as ciências da Terra e atmosfera, na agricultura, nas ciências dos solos e hidrologia, estudos ambientais e mais recentemente na epidemiologia. 12/4/2020 4

Parte 1 Introdução / Motivação O que é geoestatística? É uma abordagem PROBABILÍSTICA de modelagem, que engloba um conjunto de métodos estatísticos, para a análise e mapeamento de dados distribuídos no espaço e/ou no tempo. Requer o conhecimento de alguns conceitos básicos: • Variável aleatória (V. A. ) • Momentos da V. A. Exs: E[X]), C[X, Y]; • Função densidade de probabilidade (FDP); • Função de Distribuição Acumulada (FDA): univariada e bivariada; • Função aleatória (FA), etc. 12/4/2020 5

Parte 1 Introdução / Motivação A modelagem geoestatística envolve três etapas: 1) Análise: objetiva descrever a variabilidade espacial do fenômeno em estudo, denominada de análise estrutural ou modelagem do semivariograma. 2) Inferência: objetiva estimar valores de uma variável distribuída no espaço em locais não amostrados, denominada de krigeagem. 3) Simulação: objetiva construir um conjunto de realizações equiprováveis ou igualmente representativa do fenômeno em estudo. 12/4/2020 6

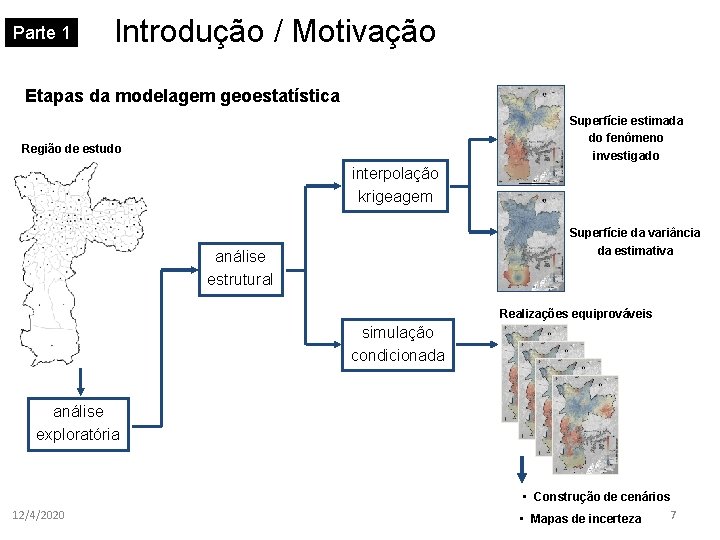
Parte 1 Introdução / Motivação Etapas da modelagem geoestatística Superfície estimada do fenômeno investigado Região de estudo interpolação krigeagem Superfície da variância da estimativa análise estrutural Realizações equiprováveis simulação condicionada análise exploratória 12/4/2020 • Construção de cenários 7 • Mapas de incerteza

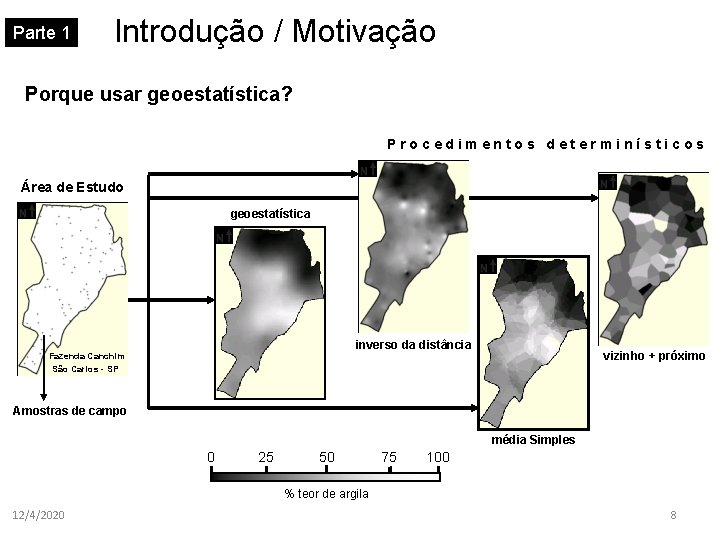
Parte 1 Introdução / Motivação Porque usar geoestatística? Procedimentos determinísticos Área de Estudo geoestatística inverso da distância Fazenda Canchim São Carlos - SP vizinho + próximo Amostras de campo média Simples 0 25 50 75 100 % teor de argila 12/4/2020 8

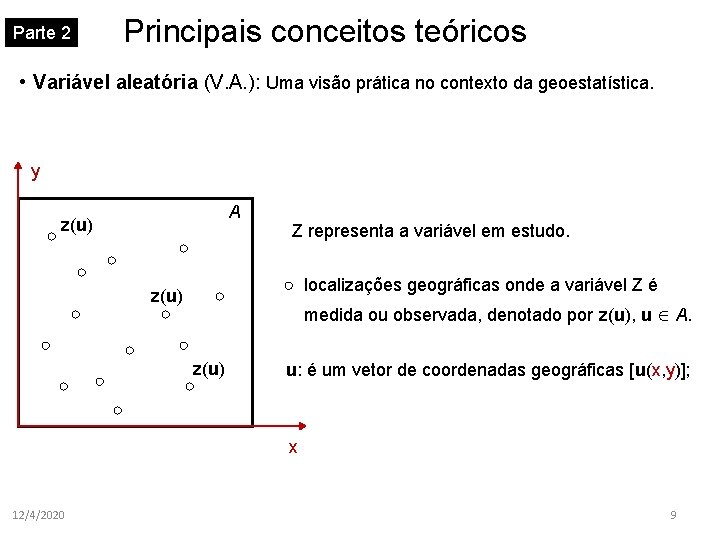
Parte 2 Principais conceitos teóricos • Variável aleatória (V. A. ): Uma visão prática no contexto da geoestatística. y A z(u) Z representa a variável em estudo. localizações geográficas onde a variável Z é z(u) medida ou observada, denotado por z(u), u A. z(u) u: é um vetor de coordenadas geográficas [u(x, y)]; x 12/4/2020 9

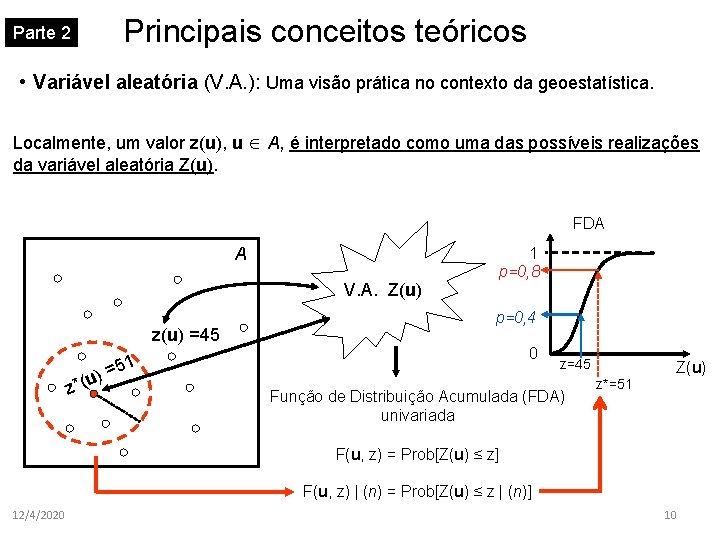
Parte 2 Principais conceitos teóricos • Variável aleatória (V. A. ): Uma visão prática no contexto da geoestatística. Localmente, um valor z(u), u A, é interpretado como uma das possíveis realizações da variável aleatória Z(u). FDA A V. A. Z(u) z(u) =45 z*(u 1 p=0, 8 p=0, 4 0 1 ) =5 z=45 Função de Distribuição Acumulada (FDA) univariada Z(u) z*=51 F(u, z) = Prob[Z(u) ≤ z] F(u, z) | (n) = Prob[Z(u) ≤ z | (n)] 12/4/2020 10

Parte 2 Principais conceitos teóricos • Função aleatória (F. A. ): Uma visão prática no contexto da geoestatística. O conjunto de V. A. , {Z(u), u A}, é uma F. A. Z(u). Na geoestatística um caso de particular interesse de F. A. é a FDA bivariada. A z(u+h) F(u, u+h; z 1, z 2) = Prob[Z(u) ≤ z 1, Z(u+h) ≤ z 2] h z(u) Momento da FDA bivariada: Covariância C[Z(u), Z(u+h)] = E[Z(u). Z(u+h)] – E[Z(u)]. E[Z(u+h)] h é um vetor distância entre dois pontos. 12/4/2020 11

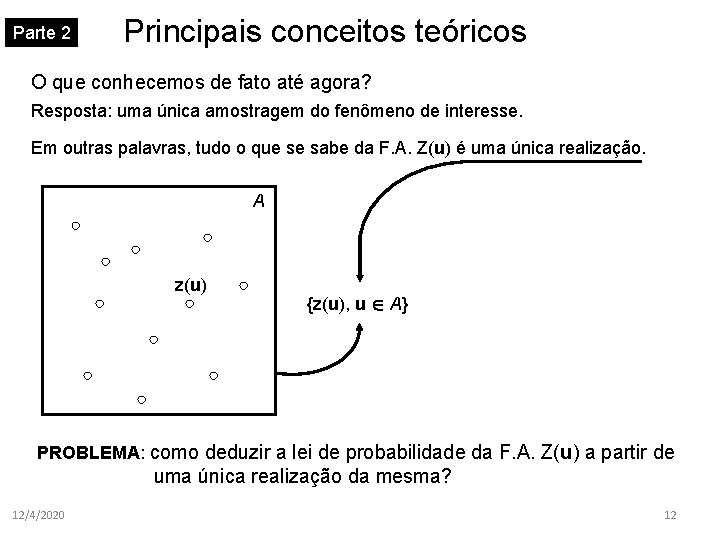
Parte 2 Principais conceitos teóricos O que conhecemos de fato até agora? Resposta: uma única amostragem do fenômeno de interesse. Em outras palavras, tudo o que se sabe da F. A. Z(u) é uma única realização. A z(u) {z(u), u A} PROBLEMA: como deduzir a lei de probabilidade da F. A. Z(u) a partir de uma única realização da mesma? 12/4/2020 12

Parte 2 Principais conceitos teóricos O paradigma que se estabelece, para inferir as FDA e interpolar valores em localizações não amostradas, é o de assumir a hipótese de estacionariedade. • a estacionariedade é uma propriedade do modelo probabilístico, uma hipótese necessária para realização de inferências; • não é uma característica do fenômeno espacial em estudo; • é uma decisão feita pelo analista, afim de verificar a adequação do modelo à realidade a ser investigada. 12/4/2020 13

Parte 2 Principais conceitos teóricos Hipótese de estacionariedade de 2 a ordem Considera somente o primeiro e o segundo momentos invariantes da F. A. 1) E[Z(u)] = m, u A E[Z(u)] = E[Z(u+h)] = m ou E[Z(u)] - E[Z(u+h)] = E[Z(u) - Z(u+h)] = 0 A z(u) h z(u+h) 12/4/2020 14

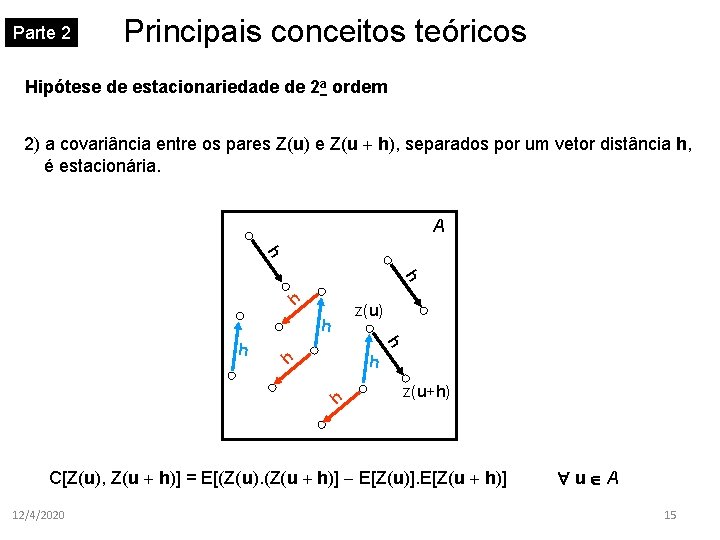
Parte 2 Principais conceitos teóricos Hipótese de estacionariedade de 2 a ordem 2) a covariância entre os pares Z(u) e Z(u + h), separados por um vetor distância h, é estacionária. A h h h z(u) h h h z(u+h) C[Z(u), Z(u + h)] = E[(Z(u). (Z(u + h)] - E[Z(u)]. E[Z(u + h)] 12/4/2020 u A 15

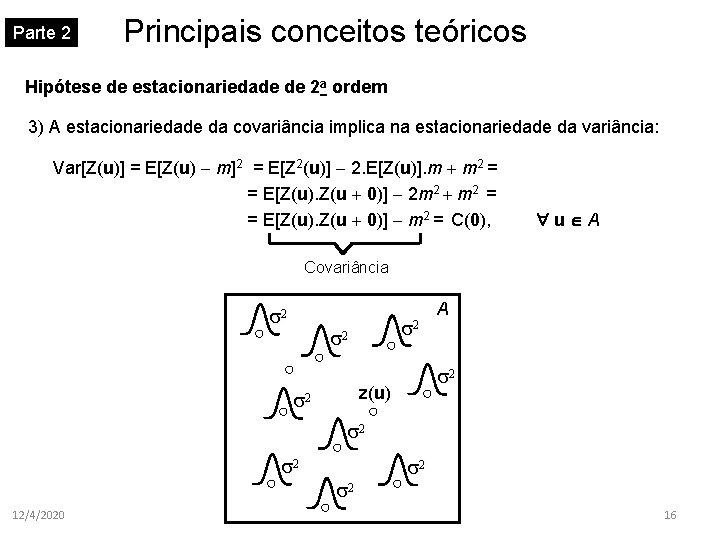
Parte 2 Principais conceitos teóricos Hipótese de estacionariedade de 2 a ordem 3) A estacionariedade da covariância implica na estacionariedade da variância: Var[Z(u)] = E[Z(u) - m]2 = E[Z 2(u)] - 2. E[Z(u)]. m + m 2 = = E[Z(u). Z(u + 0)] - 2 m 2 + m 2 = = E[Z(u). Z(u + 0)] - m 2 = C(0), u A Covariância 2 2 z(u) 2 A 2 2 12/4/2020 2 2 16

Parte 2 Principais conceitos teóricos Hipótese de estacionariedade intrínseca estabelece que os incrementos [Z(u) - Z(u + h)] tem esperança zero e variância somente em função de h, assim: 1) E[Z(u) - Z(u + h)]=0 , u A. 2) Var[Z(u) - Z(u + h)] = E{[Z(u) - Z(u + h)]2} = 2 (h) em que: 2 (h) é denominado de função variograma e (h) de semivariograma (h) = C(0) - C(h) a covariância C(h) e o semivariograma (h) são ferramentas equivalentes para caracterizar a dependência espacial. 12/4/2020 17

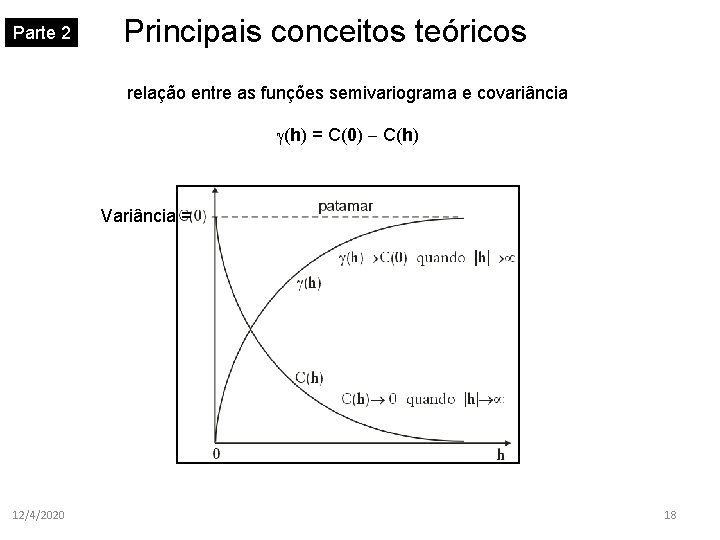
Parte 2 Principais conceitos teóricos relação entre as funções semivariograma e covariância (h) = C(0) - C(h) Variância = 12/4/2020 18

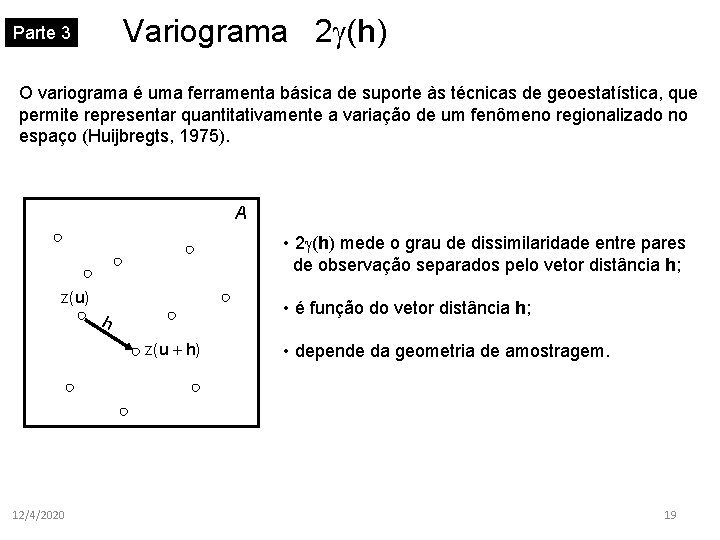
Variograma 2 (h) Parte 3 O variograma é uma ferramenta básica de suporte às técnicas de geoestatística, que permite representar quantitativamente a variação de um fenômeno regionalizado no espaço (Huijbregts, 1975). A • 2 (h) mede o grau de dissimilaridade entre pares de observação separados pelo vetor distância h; z(u) • é função do vetor distância h; h z(u + h) 12/4/2020 • depende da geometria de amostragem. 19

Parte 3 Variograma 2 (h) Definição: esperança matemática (E) do quadrado da diferença entre os valores de pontos no espaço separados pelo vetor distância h. 2 (h) = E{[z(u) - z(u + h)]2} Através de um conjunto amostral, {z(u 1), z(u 2), . . . , z(u. N)}, o variograma pode ser estimado por: 2 ^(h) = 1 N(h) i=1 å [ z(ui) - z(ui + h)]2 em que: 2 ^(h): é o estimador de variograma; h: é o vetor distância (modulo e direção) entre pares de observação; N(h): é o número de pares, z(ui) e z(ui + h), separados por h; z(ui) e z(ui + h): são valores observados nas localizações ui e ui + h. 12/4/2020 20

Parte 3 Semivariograma (h) Definição: metade da esperança matemática (E) do quadrado da diferença entre os valores de pontos no espaço separados pelo vetor distância h. (h) = 1 E{[z(u) - z(u + h)]2} 2 Através de um conjunto amostral, {z(u 1), z(u 2), . . . , z(u. N)}, o semivariograma pode ser estimado por: ^ (h) = 1 2 N(h) å [ z(ui) - z(ui + h)]2 i=1 em que: ^(h): é o estimador de semivariograma; h, N(h), z(ui) e z(ui + h): conforme definidos anteriormente. 12/4/2020 21

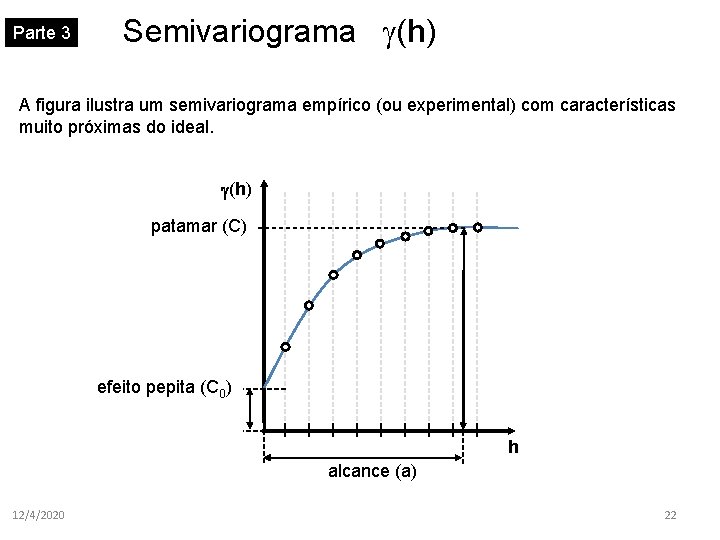
Parte 3 Semivariograma (h) A figura ilustra um semivariograma empírico (ou experimental) com características muito próximas do ideal. (h) patamar (C) efeito pepita (C 0) h alcance (a) 12/4/2020 22

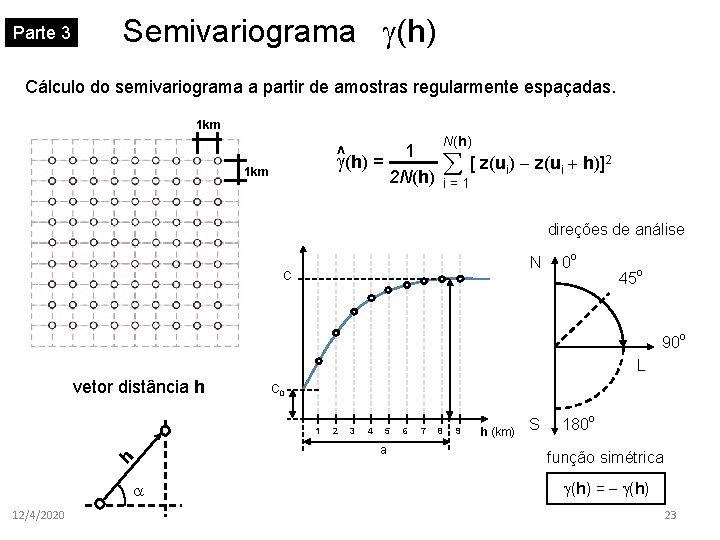
Parte 3 Semivariograma (h) Cálculo do semivariograma a partir de amostras regularmente espaçadas. 1 km N(h) ^ (h) = 1 2 N(h) 1 km å [ z(ui) - z(ui + h)]2 i=1 direções de análise N C 0 o 45 o 90 o L vetor distância h C 0 1 2 3 4 5 h a a 12/4/2020 6 7 8 9 h (km) S 180 o função simétrica (h) = - (h) 23

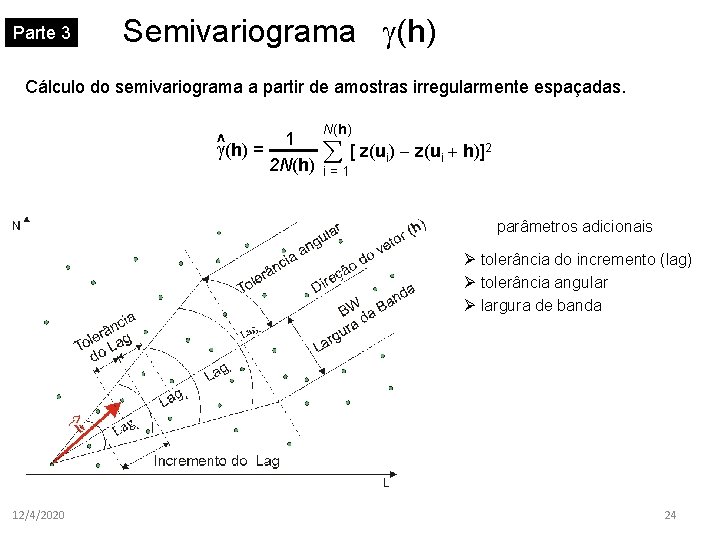
Parte 3 Semivariograma (h) Cálculo do semivariograma a partir de amostras irregularmente espaçadas. ^ (h) = 1 2 N(h) å [ z(ui) - z(ui + h)]2 i=1 parâmetros adicionais Ø tolerância do incremento (lag) Ø tolerância angular Ø largura de banda 12/4/2020 24

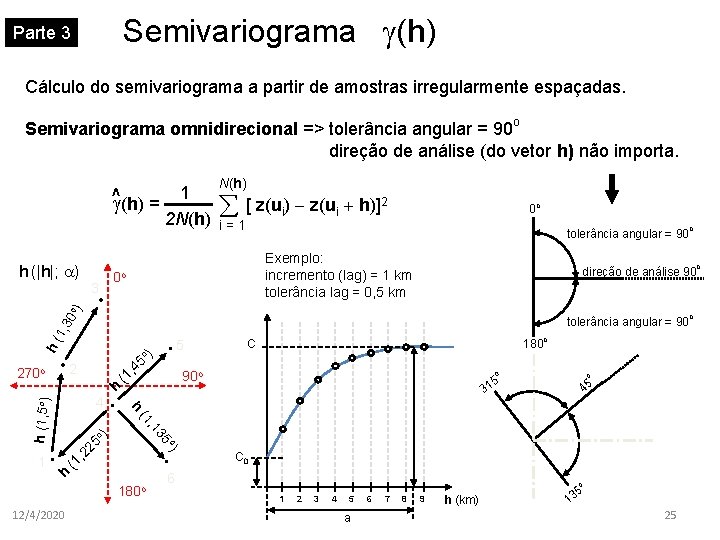
Semivariograma (h) Parte 3 Cálculo do semivariograma a partir de amostras irregularmente espaçadas. Semivariograma omnidirecional => tolerância angular = 90 o direção de análise (do vetor h) não importa. ^ (h) = 1 2 N(h) h (|h|; a) o tolerância angular = 90 Exemplo: incremento (lag) = 1 km tolerância lag = 0, 5 km 1, 3 0 o) o direção de análise 90 o h( tolerância angular = 90 o 45 ) • 5 , o ) 90 o o) 2 , (1 25 (1 180 o C o o 5 31 45 35 , 1 (1 h (1, 5 o) h 4 • 180 o 12/4/2020 i=1 • • 2 h 0 o h 1 • å [ z(ui) - z(ui + h)]2 0 o 3 270 o N(h) • 6 C 0 o 1 2 3 4 5 a 6 7 8 9 h (km) 35 1 25

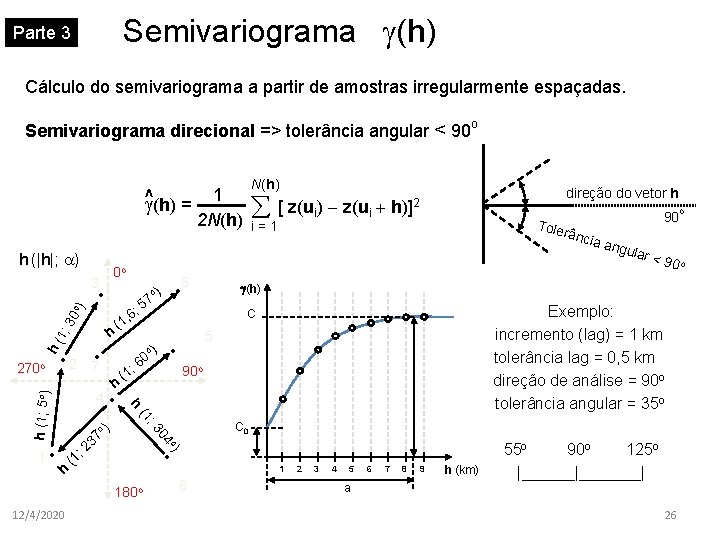
Semivariograma (h) Parte 3 Cálculo do semivariograma a partir de amostras irregularmente espaçadas. Semivariograma direcional => tolerância angular < 90 o N(h) ^ (h) = 1 2 N(h) h (|h|; a) 0 o 3 30 o ) • 1; • 12/4/2020 r<9 0 o Exemplo: incremento (lag) = 1 km tolerância lag = 0, 5 km direção de análise = 90 o tolerância angular = 35 o o) • 180 o gula C 0 04 h 2 ) ; 3 (1 o 37 • ia an (h) 90 o (1 90 rânc 5 • 0 ; 6 h Tole i=1 C o) 7 4 ; (1 , 6 (1 57 o h 1 • ; h h( • 2 h (1; 5 o) 270 o 8 • o) å [ z(ui) - z(ui + direção do vetor h h)]2 1 6 2 3 4 5 a 6 7 8 9 h (km) 55 o 90 o 125 o |_______| 26

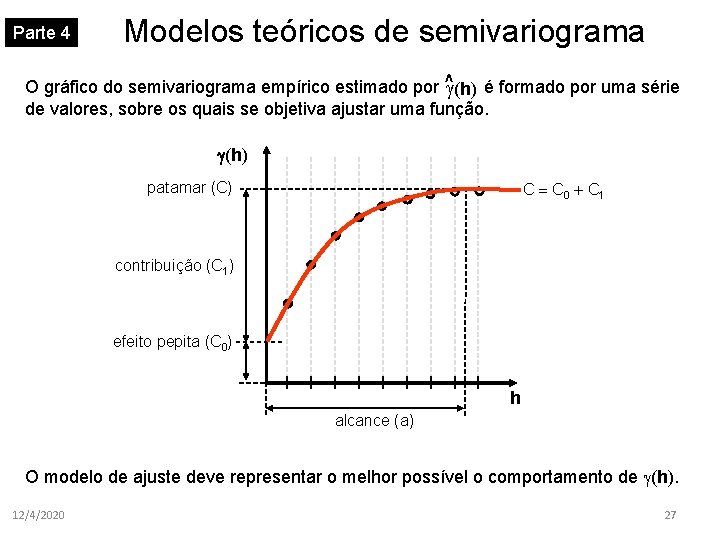
Parte 4 Modelos teóricos de semivariograma O gráfico do semivariograma empírico estimado por ^ (h) é formado por uma série de valores, sobre os quais se objetiva ajustar uma função. (h) patamar (C) C C 0 + C 1 contribuição (C 1) efeito pepita (C 0) h alcance (a) O modelo de ajuste deve representar o melhor possível o comportamento de (h). 12/4/2020 27

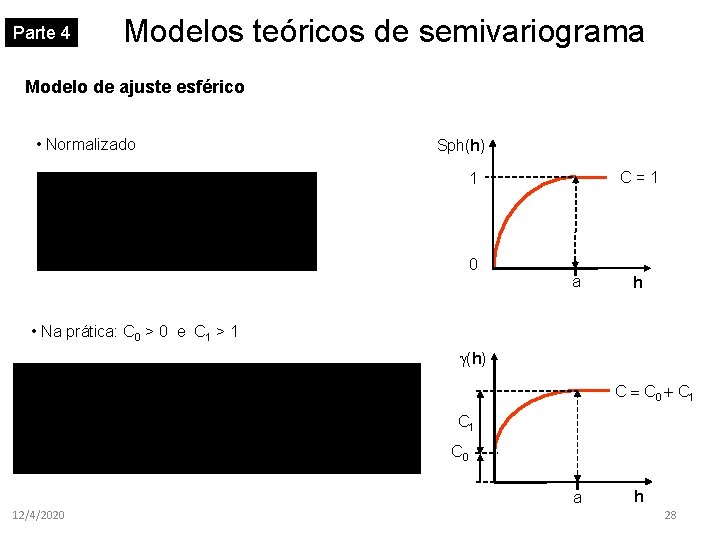
Parte 4 Modelos teóricos de semivariograma Modelo de ajuste esférico • Normalizado Sph(h) C=1 1 0 a h • Na prática: C 0 > 0 e C 1 > 1 (h) C C 0 + C 1 C 0 a 12/4/2020 h 28

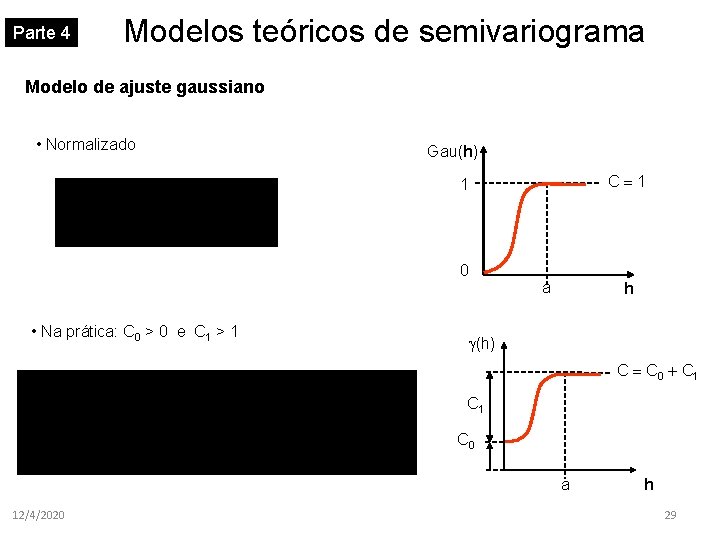
Parte 4 Modelos teóricos de semivariograma Modelo de ajuste gaussiano • Normalizado Gau(h) C 1 1 0 • Na prática: C 0 > 0 e C 1 > 1 a h (h) C C 0 + C 1 C 0 a 12/4/2020 h 29

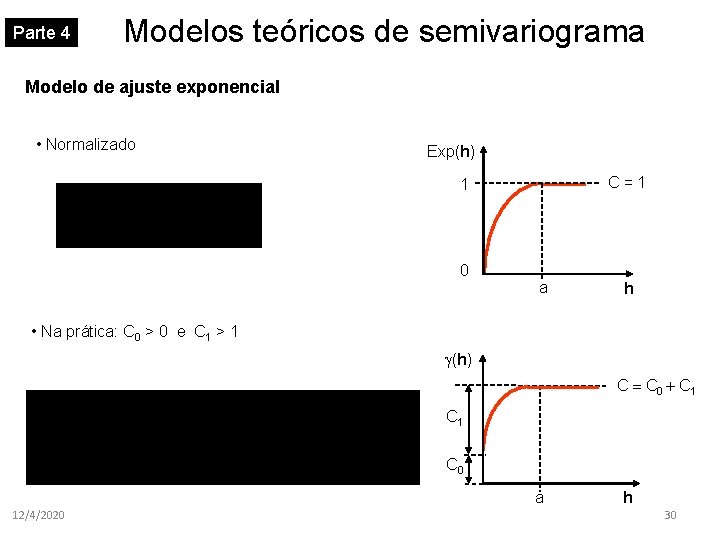
Parte 4 Modelos teóricos de semivariograma Modelo de ajuste exponencial • Normalizado Exp(h) C=1 1 0 a h • Na prática: C 0 > 0 e C 1 > 1 (h) C C 0 + C 1 C 0 a 12/4/2020 h 30

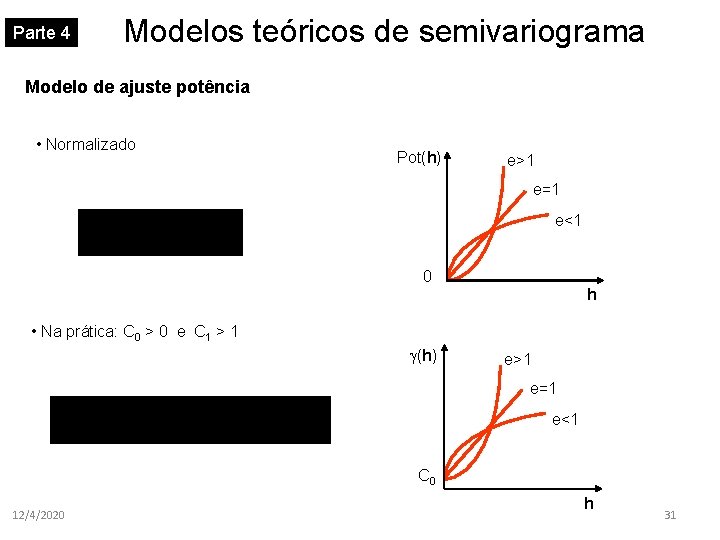
Parte 4 Modelos teóricos de semivariograma Modelo de ajuste potência • Normalizado Pot(h) e>1 e=1 e<1 0 h • Na prática: C 0 > 0 e C 1 > 1 (h) e>1 e=1 e<1 C 0 12/4/2020 h 31

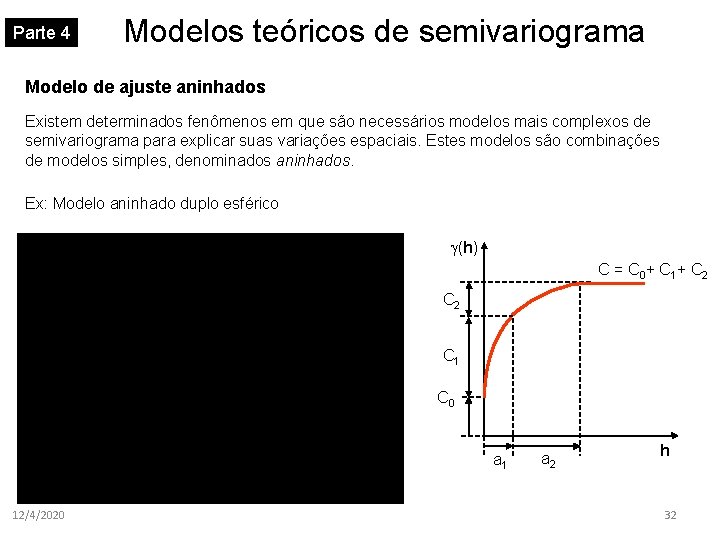
Parte 4 Modelos teóricos de semivariograma Modelo de ajuste aninhados Existem determinados fenômenos em que são necessários modelos mais complexos de semivariograma para explicar suas variações espaciais. Estes modelos são combinações de modelos simples, denominados aninhados. Ex: Modelo aninhado duplo esférico (h) C = C 0+ C 1+ C 2 C 1 C 0 a 1 12/4/2020 a 2 h 32

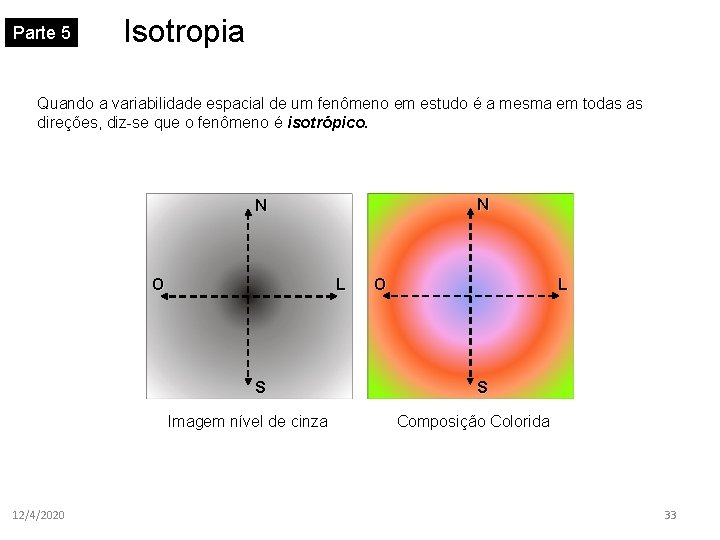
Parte 5 Isotropia Quando a variabilidade espacial de um fenômeno em estudo é a mesma em todas as direções, diz-se que o fenômeno é isotrópico. N N O L S Imagem nível de cinza 12/4/2020 O L S Composição Colorida 33

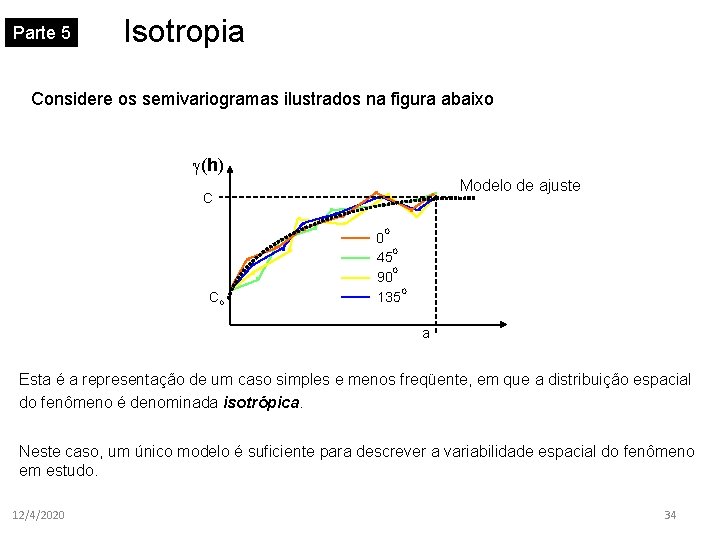
Parte 5 Isotropia Considere os semivariogramas ilustrados na figura abaixo (h) C • • Co • • • • • • • Modelo de ajuste • • • • O 0 O 45 O 90 O 135 a Esta é a representação de um caso simples e menos freqüente, em que a distribuição espacial do fenômeno é denominada isotrópica. Neste caso, um único modelo é suficiente para descrever a variabilidade espacial do fenômeno em estudo. 12/4/2020 34

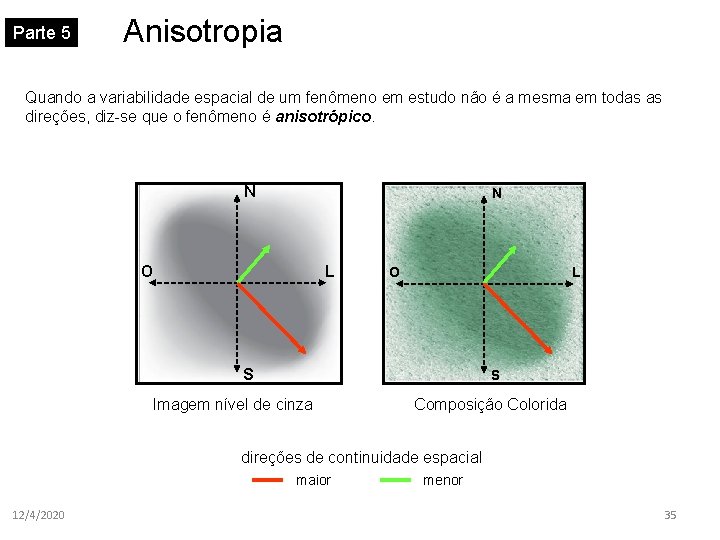
Parte 5 Anisotropia Quando a variabilidade espacial de um fenômeno em estudo não é a mesma em todas as direções, diz-se que o fenômeno é anisotrópico. N N O L S S Imagem nível de cinza Composição Colorida direções de continuidade espacial maior 12/4/2020 menor 35

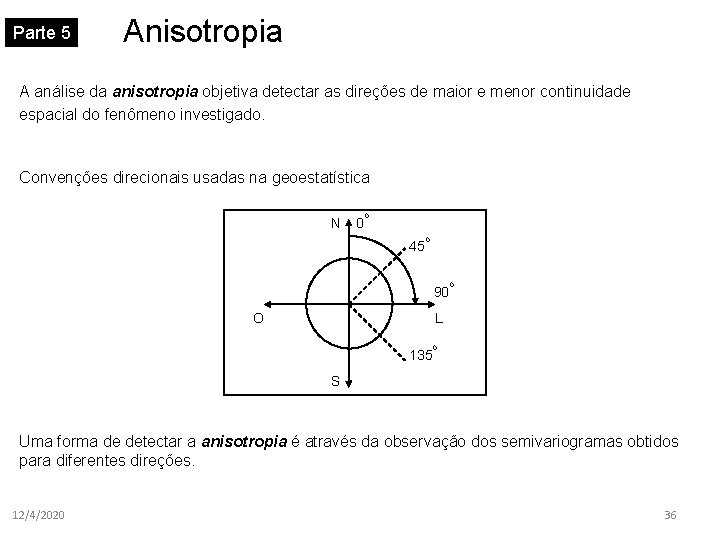
Parte 5 Anisotropia A análise da anisotropia objetiva detectar as direções de maior e menor continuidade espacial do fenômeno investigado. Convenções direcionais usadas na geoestatística N 0 o 45 o 90 O o L 135 o S Uma forma de detectar a anisotropia é através da observação dos semivariogramas obtidos para diferentes direções. 12/4/2020 36

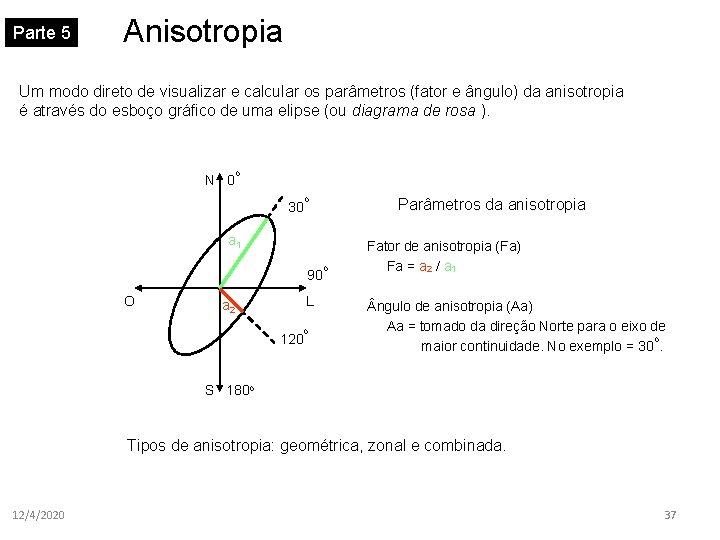
Parte 5 Anisotropia Um modo direto de visualizar e calcular os parâmetros (fator e ângulo) da anisotropia é através do esboço gráfico de uma elipse (ou diagrama de rosa ). N 0 o 30 o Parâmetros da anisotropia a 1 90 O L a 2 120 o o Fator de anisotropia (Fa) Fa = a 2 / a 1 ngulo de anisotropia (Aa) Aa = tomado da direção Norte para o eixo de o maior continuidade. No exemplo = 30. S 180 o Tipos de anisotropia: geométrica, zonal e combinada. 12/4/2020 37

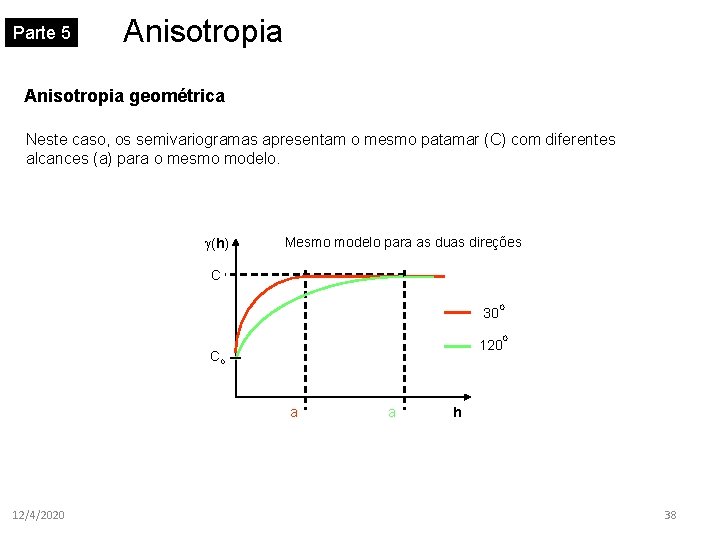
Parte 5 Anisotropia geométrica Neste caso, os semivariogramas apresentam o mesmo patamar (C) com diferentes alcances (a) para o mesmo modelo. (h) Mesmo modelo para as duas direções C 30 120 Co a 12/4/2020 O a O h 38

Parte 5 Anisotropia zonal Neste caso, os semivariogramas apresentam diferentes patamares (C) com mesmo alcance (a) para o mesmo modelo. Como a isotropia, a anisotropia zonal é um caso menos freqüente presente nos fenômenos naturais. (h) Mesmo modelo para as duas direções C C 60 Co 150 a 12/4/2020 O O h 39

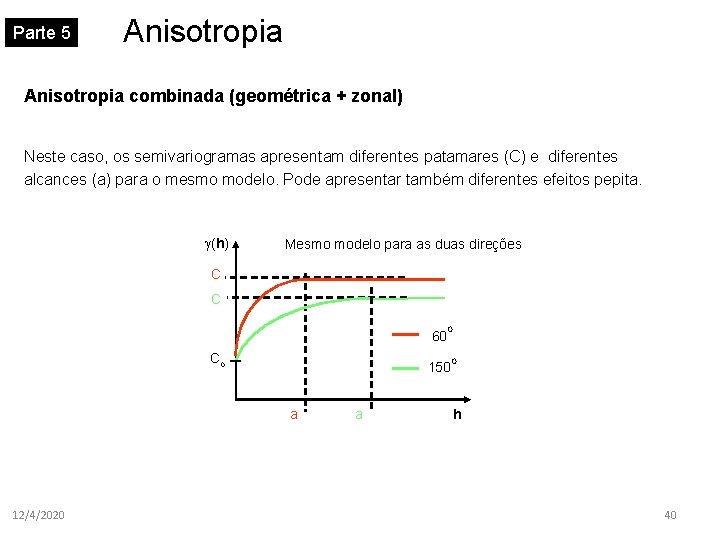
Parte 5 Anisotropia combinada (geométrica + zonal) Neste caso, os semivariogramas apresentam diferentes patamares (C) e diferentes alcances (a) para o mesmo modelo. Pode apresentar também diferentes efeitos pepita. (h) Mesmo modelo para as duas direções C C 60 Co 150 a 12/4/2020 O a O h 40

Parte 3 Semivariograma de superfície É um gráfico 2 D que fornece uma visão geral da variabilidade espacial do fenômeno em estudo. Também conhecido como Mapa de Semivariograma. Utilizado para detectar os eixos de Anisotropia (direções de maior e menor continuidade espacial). N 0 o ângulo de anisotropia L 90 o 12/4/2020 41

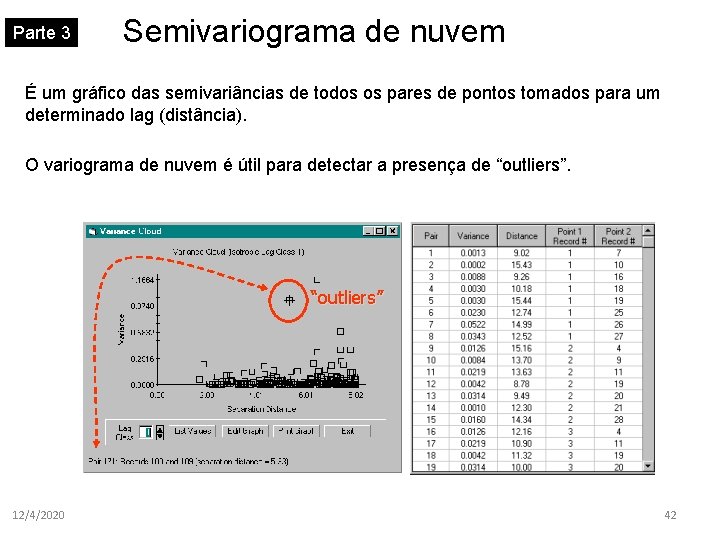
Parte 3 Semivariograma de nuvem É um gráfico das semivariâncias de todos os pares de pontos tomados para um determinado lag (distância). O variograma de nuvem é útil para detectar a presença de “outliers” 12/4/2020 42

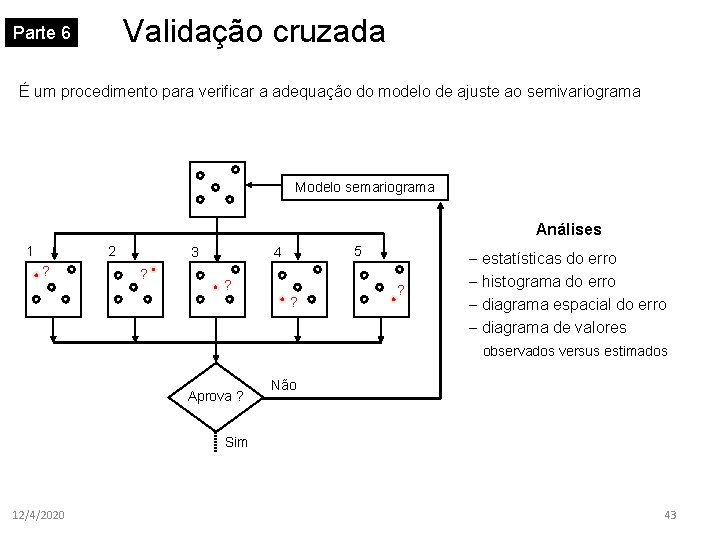
Validação cruzada Parte 6 É um procedimento para verificar a adequação do modelo de ajuste ao semivariograma Modelo semariograma Análises 1 2 ? 3 ? 5 4 ? ? ? – estatísticas do erro – histograma do erro – diagrama espacial do erro – diagrama de valores observados versus estimados Aprova ? Não Sim 12/4/2020 43

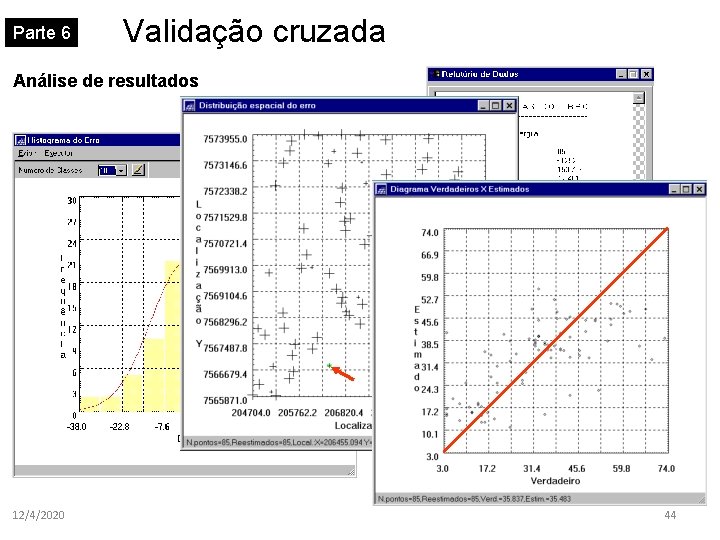
Parte 6 Validação cruzada Análise de resultados 12/4/2020 44

Parte 7 Krigeagem O termo krigeagem é derivado do nome Daniel G. Krige A krigeagem é um estimador estocástico que depende da análise de correlação espacial baseada em semivariograma. Áreas de Aplicações: Ø mapeamento geológico (Verly et al. , 1984) Ø mapeamento solo (Burgess e Webster, 1980) Ø mapeamento hidrológico (Kitanidis et. al. , 1983) Ø mapeamento atmosférico (Lajaunie, 1984) A krigeagem engloba um conjunto de estimadores: • krigeagem Simples (*) • krigeagem Ordinária (*) • krigeagem Universal • krigeagem por indicação 12/4/2020 • co-krigeagem • Outros 45

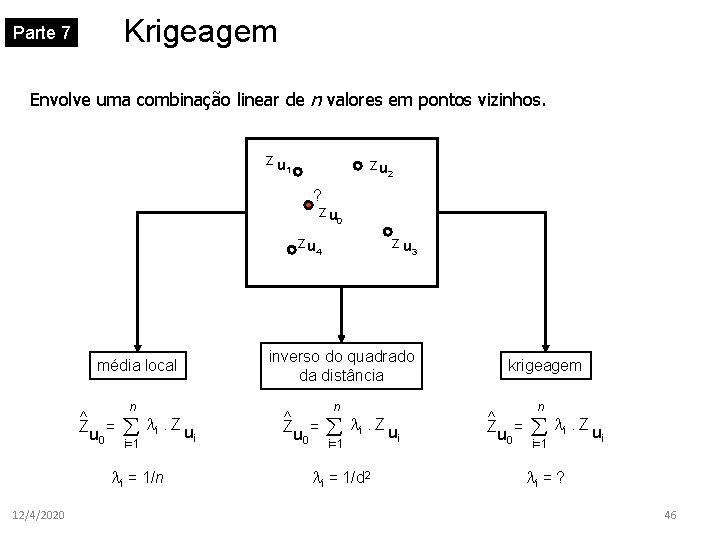
Krigeagem Parte 7 Envolve uma combinação linear de n valores em pontos vizinhos. zu z u 2 1 ? z u 0 z u 3 z u 4 média local ^ Z n u 0 = å i. Z ui i=1 i = 1/n 12/4/2020 inverso do quadrado da distância ^ Z n u 0 = å i. Z ui i=1 i = 1/d 2 krigeagem ^ Z n u 0 = å i. Z ui i=1 i = ? 46

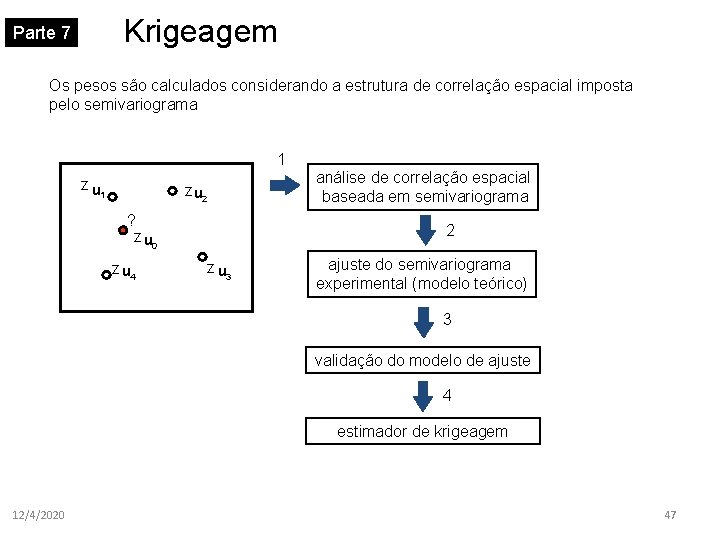
Krigeagem Parte 7 Os pesos são calculados considerando a estrutura de correlação espacial imposta pelo semivariograma 1 zu z u 2 1 ? z u 0 z u 4 análise de correlação espacial baseada em semivariograma 2 z u 3 ajuste do semivariograma experimental (modelo teórico) 3 validação do modelo de ajuste 4 estimador de krigeagem 12/4/2020 47

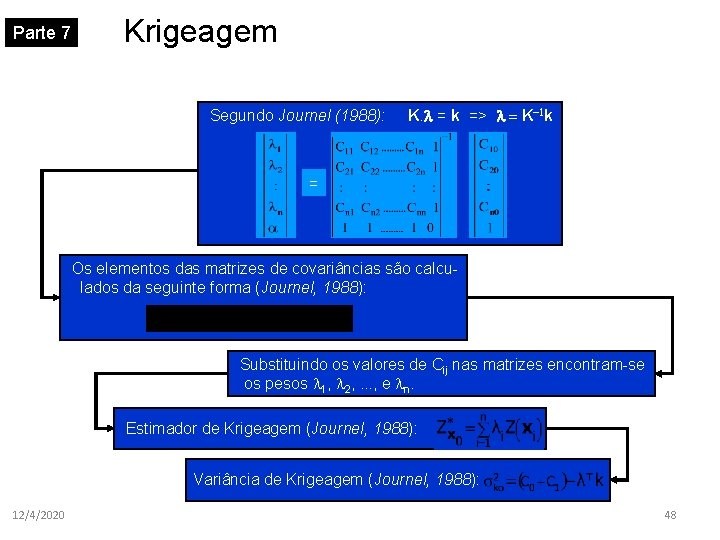
Parte 7 Krigeagem Segundo Journel (1988): K. = k => K-1 k = Os elementos das matrizes de covariâncias são calculados da seguinte forma (Journel, 1988): Substituindo os valores de Cij nas matrizes encontram-se os pesos 1, 2, . . . , e n. Estimador de Krigeagem (Journel, 1988): Variância de Krigeagem (Journel, 1988): 12/4/2020 48

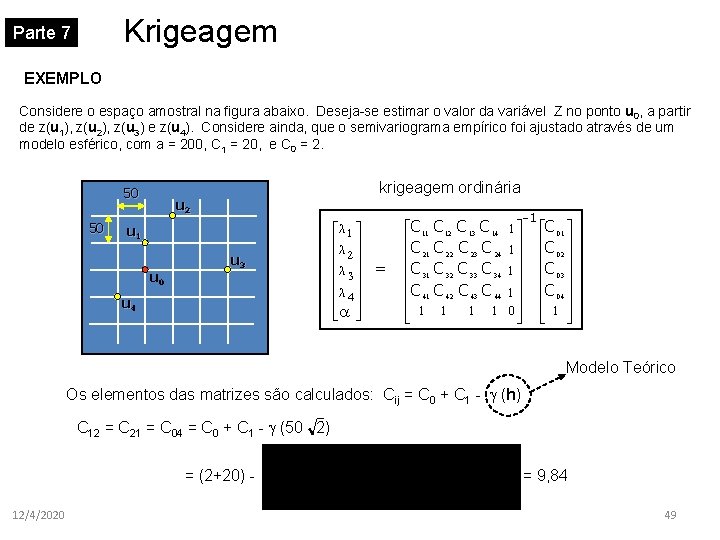
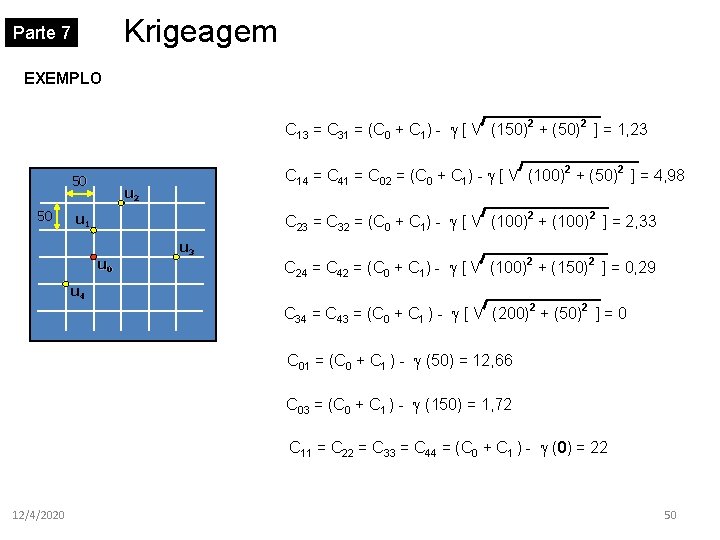
Krigeagem Parte 7 EXEMPLO Considere o espaço amostral na figura abaixo. Deseja-se estimar o valor da variável Z no ponto u 0, a partir de z(u 1), z(u 2), z(u 3) e z(u 4). Considere ainda, que o semivariograma empírico foi ajustado através de um modelo esférico, com a = 200, C 1 = 20, e C 0 = 2. 50 50 krigeagem ordinária u 2 u 1 u 0 u 3 u 4 éλ 1 ù ê ú êλ 2 ú êλ 3 ú êλ ú ê 4ú êë a úû = é C 11 C 12 ê ê C 21 C 22 ê ê C 31 C 32 ê ê C 41 C 42 ê 1 1 ë C 13 C 14 C 23 C 24 C 33 C 34 C 43 C 44 1 1ù ú 1ú 1 0ú û -1 é C 01 ù ê ú ê C 02 ú ê C 03 ú ê C 04 ú ê 1 ú ë û Modelo Teórico Os elementos das matrizes são calculados: Cij = C 0 + C 1 - (h) C 12 = C 21 = C 04 = C 0 + C 1 - (50 2) = (2+20) 12/4/2020 = 9, 84 49

Krigeagem Parte 7 EXEMPLO C 13 = C 31 = (C 0 + C 1) - [ V (150) + (50) ] = 1, 23 2 C 14 = C 41 = C 02 = (C 0 + C 1) - [ V (100) + (50) ] = 4, 98 2 50 50 2 u 2 2 C 23 = C 32 = (C 0 + C 1) - [ V (100) + (100) ] = 2, 33 2 u 1 u 0 u 3 2 C 24 = C 42 = (C 0 + C 1) - [ V (100) + (150) ] = 0, 29 2 2 u 4 C 34 = C 43 = (C 0 + C 1 ) - [ V (200) + (50) ] = 0 2 2 C 01 = (C 0 + C 1 ) - (50) = 12, 66 C 03 = (C 0 + C 1 ) - (150) = 1, 72 C 11 = C 22 = C 33 = C 44 = (C 0 + C 1 ) - (0) = 22 12/4/2020 50

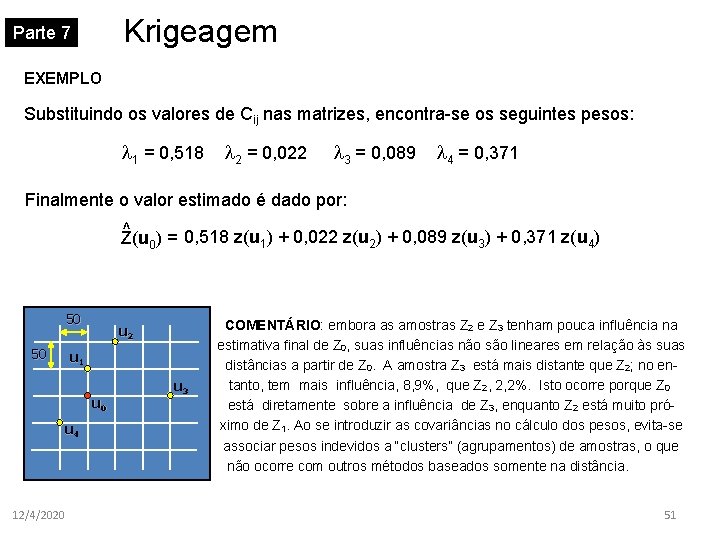
Krigeagem Parte 7 EXEMPLO Substituindo os valores de Cij nas matrizes, encontra-se os seguintes pesos: 1 = 0, 518 2 = 0, 022 3 = 0, 089 4 = 0, 371 Finalmente o valor estimado é dado por: ^ ) = 0, 518 z(u ) + 0, 022 z(u ) + 0, 089 z(u ) + 0, 371 z(u ) Z(u 1 2 3 4 0 50 50 u 2 u 1 u 0 u 4 12/4/2020 u 3 COMENTÁRIO: embora as amostras Z 2 e Z 3 tenham pouca influência na estimativa final de Z 0, suas influências não são lineares em relação às suas distâncias a partir de Z 0. A amostra Z 3 está mais distante que Z 2; no entanto, tem mais influência, 8, 9%, que Z 2, 2, 2%. Isto ocorre porque Z 0 está diretamente sobre a influência de Z 3, enquanto Z 2 está muito próximo de Z 1. Ao se introduzir as covariâncias no cálculo dos pesos, evita-se associar pesos indevidos a “clusters” (agrupamentos) de amostras, o que não ocorre com outros métodos baseados somente na distância. 51

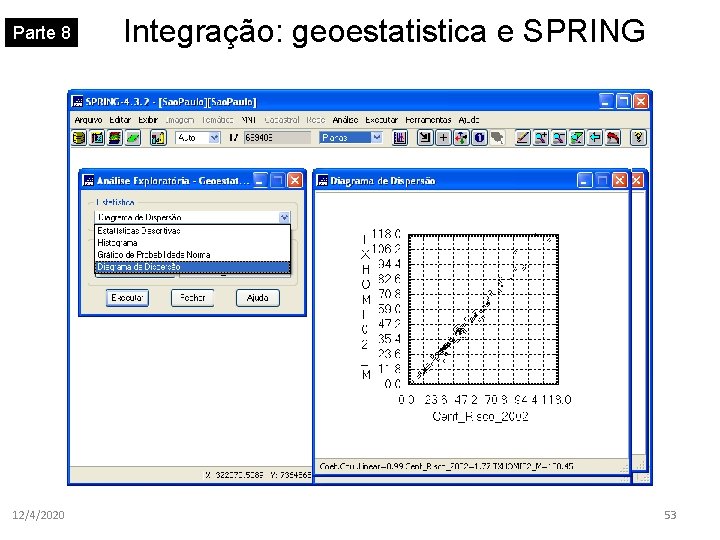
Parte 8 Integração: SPRING e geoestatistica SPRING: geoestatística 12/4/2020 52

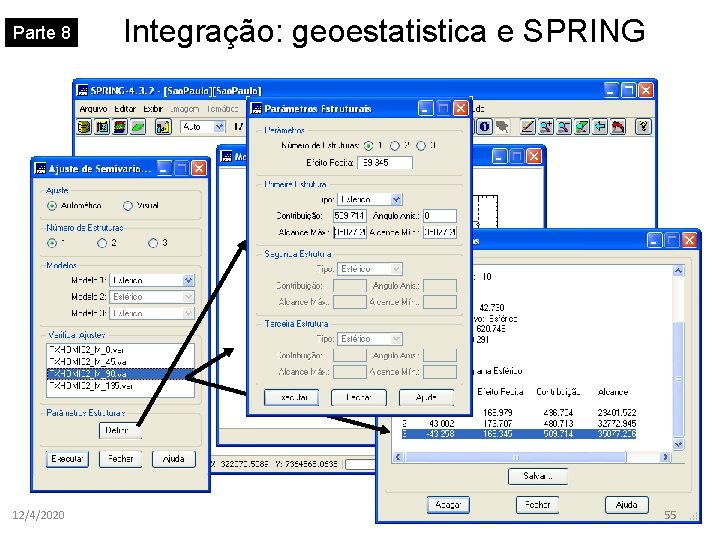
Parte 8 12/4/2020 Integração: geoestatistica e SPRING 53

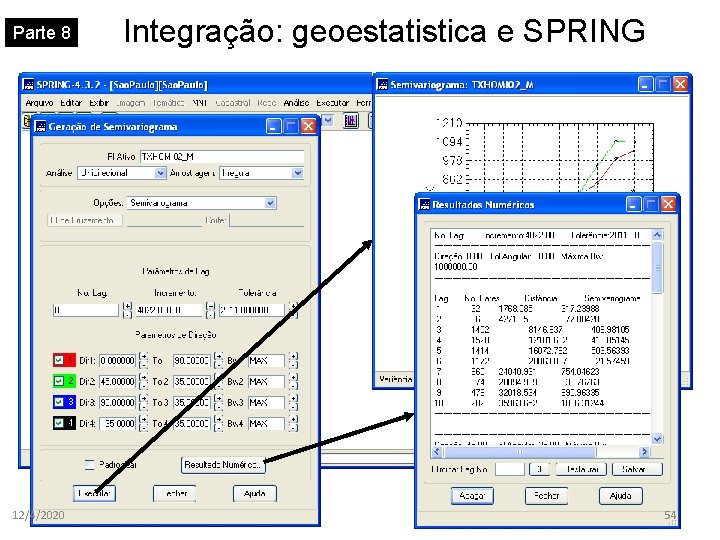
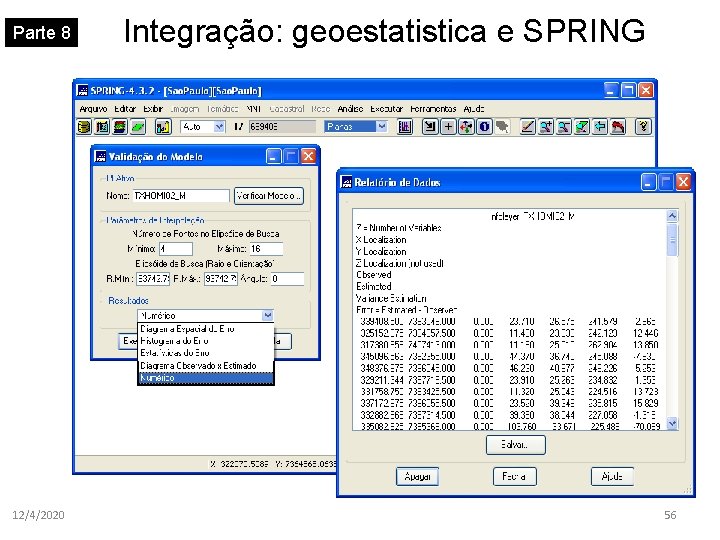
Parte 8 12/4/2020 Integração: geoestatistica e SPRING 54

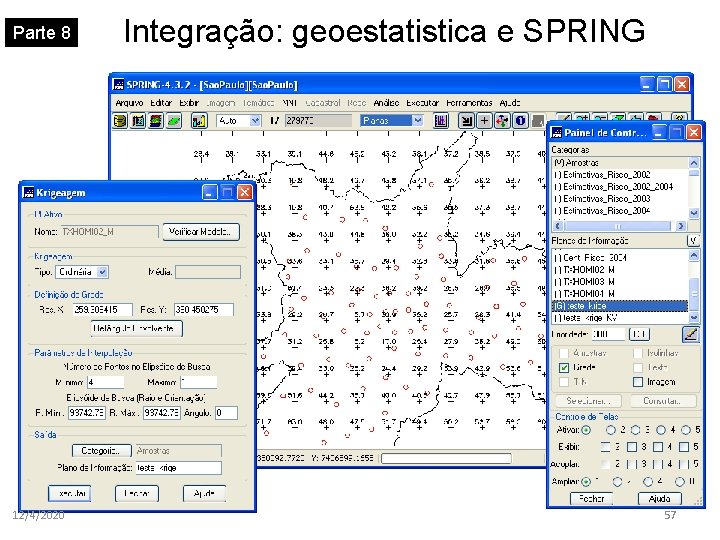
Parte 8 12/4/2020 Integração: geoestatistica e SPRING 55

Parte 8 12/4/2020 Integração: geoestatistica e SPRING 56

Parte 8 12/4/2020 Integração: geoestatistica e SPRING 57