Gauge Theory and Topological Strings Geometry Conference in




![Decomposition [C. T. C. Wall] = X X = X 0# § g b Decomposition [C. T. C. Wall] = X X = X 0# § g b](https://slidetodoc.com/presentation_image_h2/f37b8ef1f91b1feab8835e2c414ce8ee/image-7.jpg)


![CY fibered by special Lagrangian T 3 [Strominger, Yau, Zaslov] network of singularities S CY fibered by special Lagrangian T 3 [Strominger, Yau, Zaslov] network of singularities S](https://slidetodoc.com/presentation_image_h2/f37b8ef1f91b1feab8835e2c414ce8ee/image-14.jpg)


![Gauge Theory Invariants Coherent sheaf Charge E! X ¹ = [E] 2 K 0 Gauge Theory Invariants Coherent sheaf Charge E! X ¹ = [E] 2 K 0](https://slidetodoc.com/presentation_image_h2/f37b8ef1f91b1feab8835e2c414ce8ee/image-23.jpg)

![GW-DT Equivalence [Maulik, Nekrasov, Okounkov, Pandharipande] Consider the case of rank one, p = GW-DT Equivalence [Maulik, Nekrasov, Okounkov, Pandharipande] Consider the case of rank one, p =](https://slidetodoc.com/presentation_image_h2/f37b8ef1f91b1feab8835e2c414ce8ee/image-26.jpg)







![OSV Conjecture [Ooguri, Strominger, Vafa] p! 1 Consider the limit Z gau ge (p; OSV Conjecture [Ooguri, Strominger, Vafa] p! 1 Consider the limit Z gau ge (p;](https://slidetodoc.com/presentation_image_h2/f37b8ef1f91b1feab8835e2c414ce8ee/image-36.jpg)
![Black Hole Entropy (semi-classical) [Bekenstein, Hawking] Black Hole Entropy (semi-classical) [Bekenstein, Hawking]](https://slidetodoc.com/presentation_image_h2/f37b8ef1f91b1feab8835e2c414ce8ee/image-38.jpg)


![Example of OSV conjecture Local 2 -torus in CY [Vafa] X area of T Example of OSV conjecture Local 2 -torus in CY [Vafa] X area of T](https://slidetodoc.com/presentation_image_h2/f37b8ef1f91b1feab8835e2c414ce8ee/image-45.jpg)


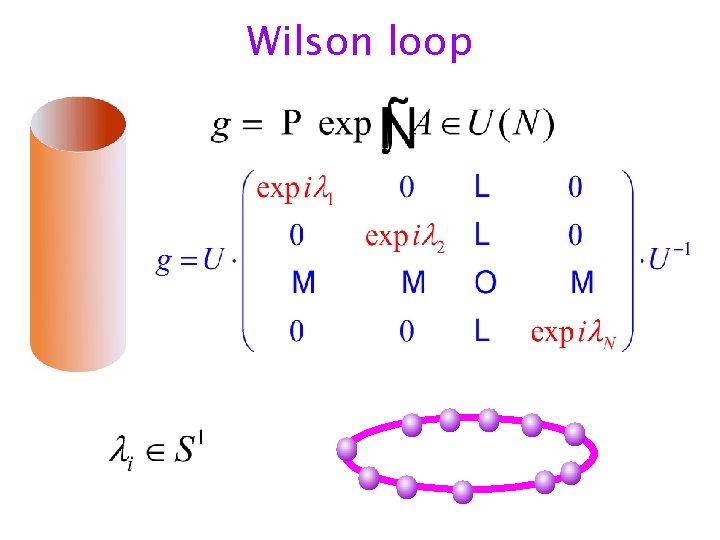





![Rank zero, divisor P p = (0; c 1 ) = (0; [P ]) Rank zero, divisor P p = (0; c 1 ) = (0; [P ])](https://slidetodoc.com/presentation_image_h2/f37b8ef1f91b1feab8835e2c414ce8ee/image-60.jpg)




- Slides: 64

Gauge Theory and Topological Strings Geometry Conference in honour of Nigel Hitchin - RHD, C. Vafa, E. Verlinde, hep-th/0602087 - J. de Boer, M. Chang, RHD, J. Manschot, E. Verlinde, hep -th/0608059 Robbert Dijkgraaf University of Amsterdam

Nigel Hitchin’s Circle of Ideas

integrable systems special holonomies self-dual geometry hyper-Kahler monopoles quantization Nigel Hitchin’s Circle of Ideas calibrations instantons mirror symmetry Higgs-bundles (generalized) CY spectral curves

integrable systems special holonomies self-dual geometry hyper-Kahler quantization monopoles calibrations instantons mirror symmetry Higgs-bundles (generalized) CY spectral curves

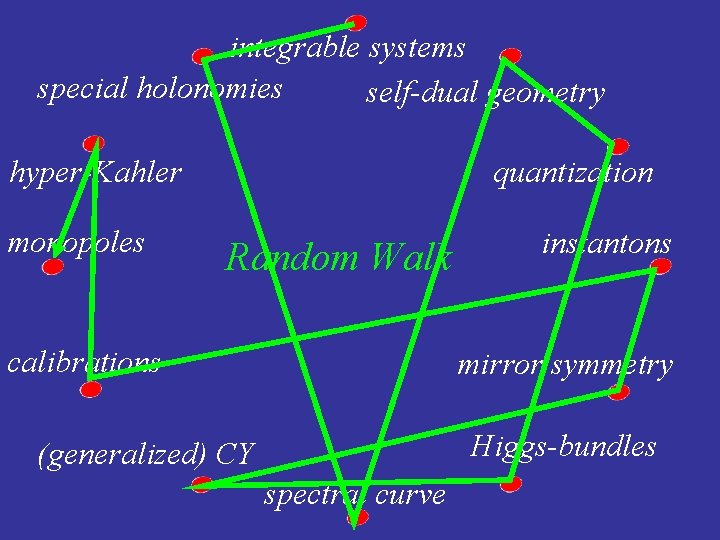
integrable systems special holonomies self-dual geometry hyper-Kahler monopoles quantization Random Walk calibrations instantons mirror symmetry Higgs-bundles (generalized) CY spectral curve

Calabi-Yau threefolds X simply-connected Kähler manifold, dim. C X=3, c 1(X) = 0, no torsion. Diffeomorphism type of X is completely fixed by b 3(X) and b 2(X)Z plus classical invariants 1 3 = t ; t 2 H 2 (X ; Z) 6 X Z 1 t ^ c 2 F 1 cl (t) = 12 X F 0 cl (t) X
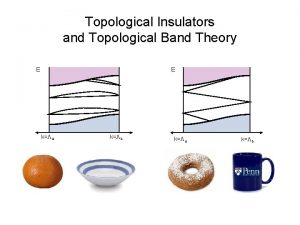
![Decomposition C T C Wall X X X 0 g b Decomposition [C. T. C. Wall] = X X = X 0# § g b](https://slidetodoc.com/presentation_image_h2/f37b8ef1f91b1feab8835e2c414ce8ee/image-7.jpg)
Decomposition [C. T. C. Wall] = X X = X 0# § g b 3 = 0 b 2 = 0 Core X 0 ¡ §g § g = # g S 3 £ S 3 ¢

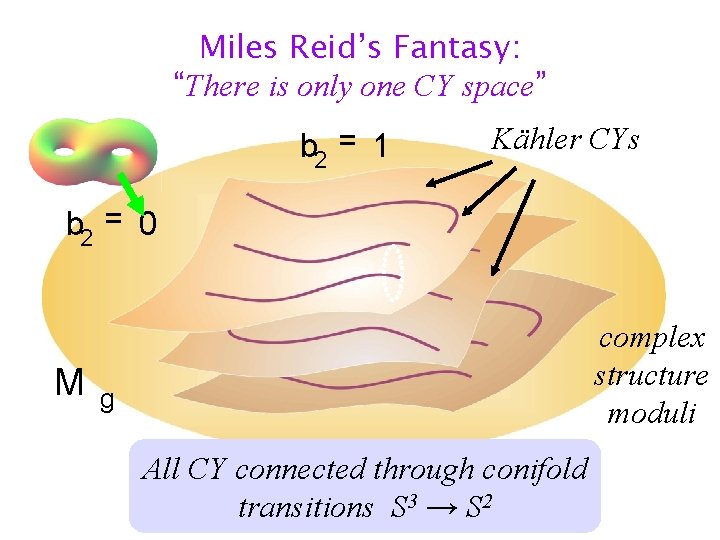
Miles Reid’s Fantasy: “There is only one CY space” b 2 = 1 Kähler CYs b 2 = 0 M complex structure moduli g All CY connected through conifold transitions S 3 → S 2

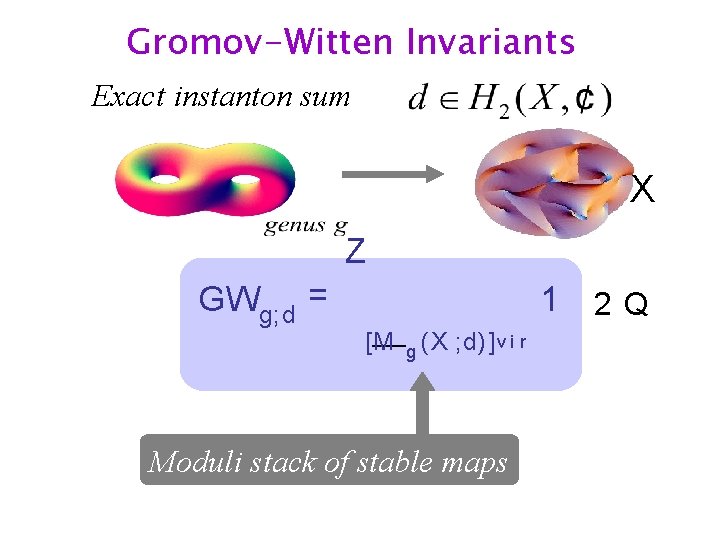
Gromov-Witten Invariants Exact instanton sum X Z GWg; d = 1 2 Q [M g (X ; d) ] v i r Moduli stack of stable maps

Topological String (A model) Quantum corrections, X t H 2(X, C) F gqu (t) = GWg; d e¡ dt d Partition function X ¸ 2 g¡ 2 F g (t) Z t op (t; ¸ ) = exp g F g (t) = F gcl (t) + F gqu (t)

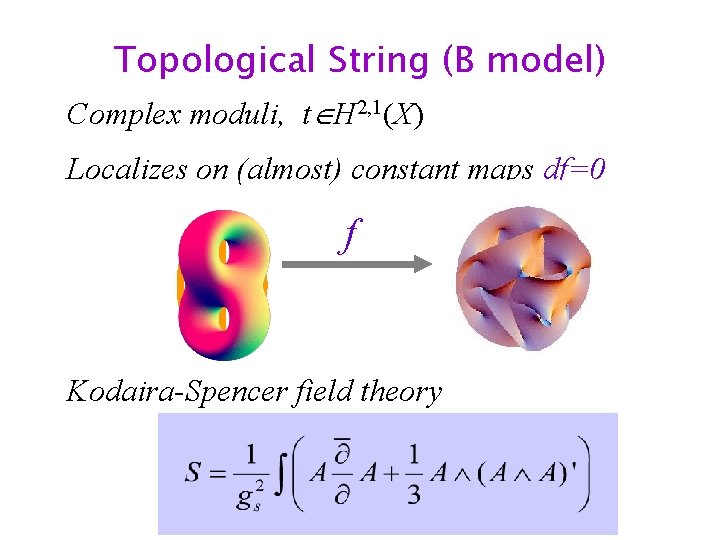
Topological String (B model) Complex moduli, t H 2, 1(X) Localizes on (almost) constant maps df=0 f Kodaira-Spencer field theory

• genus 0: classical Variation of Hodge Structures • genus 1: analytic Ray-Singer torsion • genus 2 and higher: quantum corrections quantization of. Mcomplex structure X moduli space

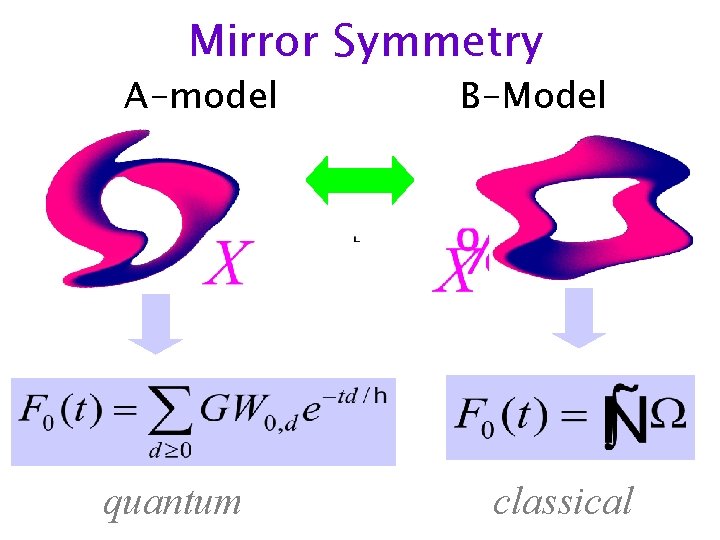
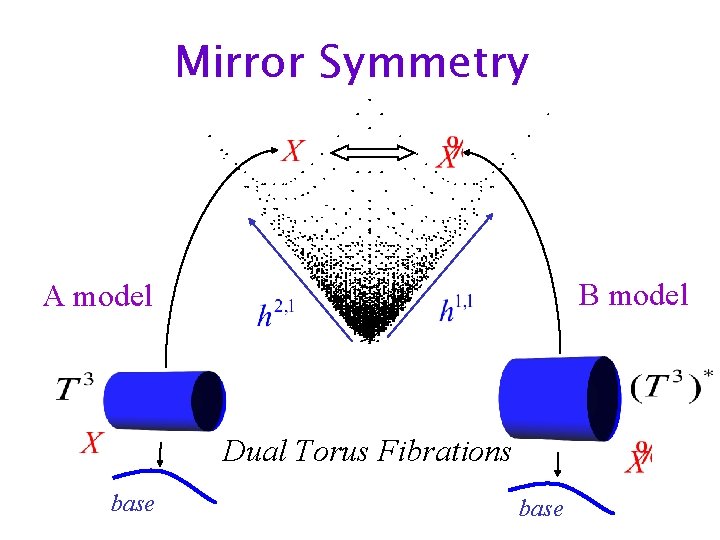
Mirror Symmetry A-model quantum B-Model classical
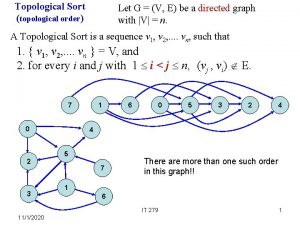
![CY fibered by special Lagrangian T 3 Strominger Yau Zaslov network of singularities S CY fibered by special Lagrangian T 3 [Strominger, Yau, Zaslov] network of singularities S](https://slidetodoc.com/presentation_image_h2/f37b8ef1f91b1feab8835e2c414ce8ee/image-14.jpg)
CY fibered by special Lagrangian T 3 [Strominger, Yau, Zaslov] network of singularities S 1 shrinks

Mirror Symmetry B model A model Dual Torus Fibrations base

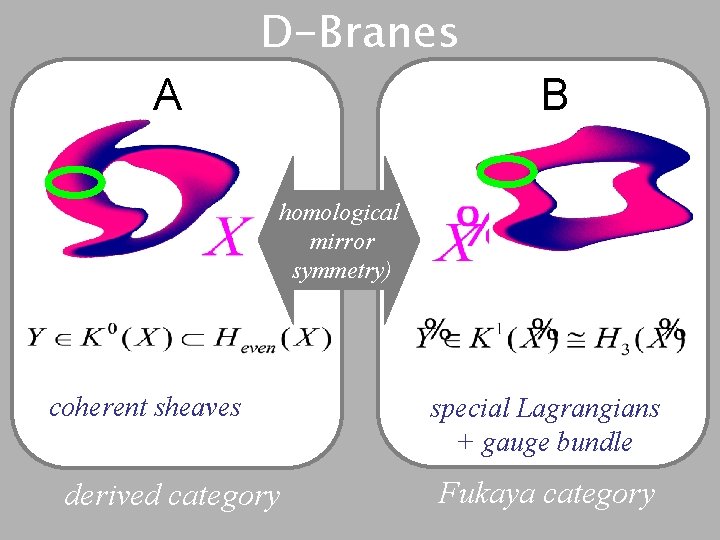
D-Branes B A homological mirror symmetry) coherent sheaves derived category special Lagrangians + gauge bundle Fukaya category

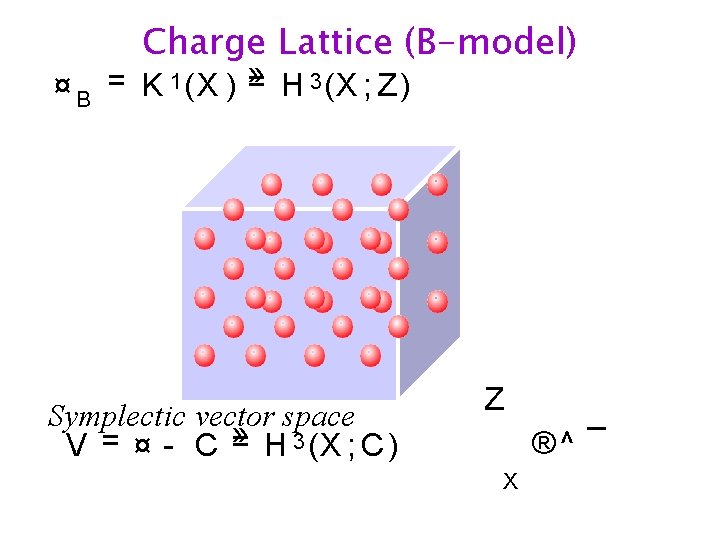
Charge Lattice (B-model) = H 3 (X ; Z) ¤ B = K 1 (X ) » Symplectic vector space = H 3 (X ; C ) V = ¤ C» Z ®^ ¯ X

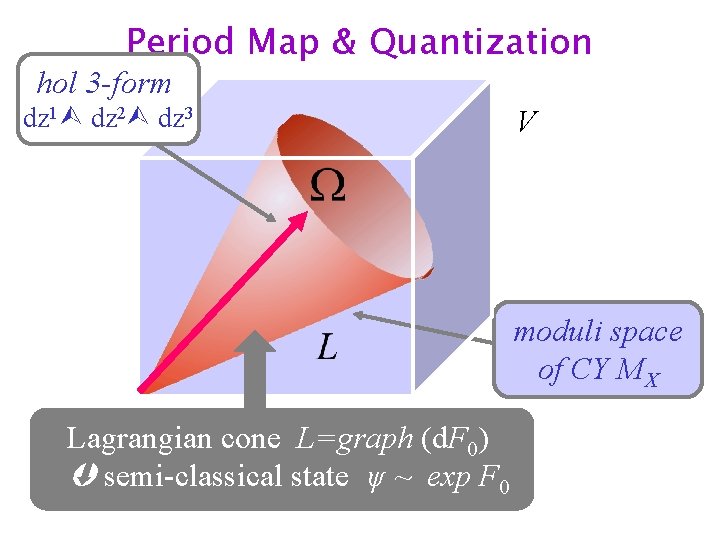
Period Map & Quantization hol 3 -form dz 1 dz 2 dz 3 V moduli space of CY MX Lagrangian cone L=graph (d. F 0) semi-classical state ψ ~ exp F 0

Special Geometry Darboux coordinates

Topological String Partition Function Transforms as a wave function (metaplectic representation) under Sp(2 n, Z) change of canonical basis (A, B)

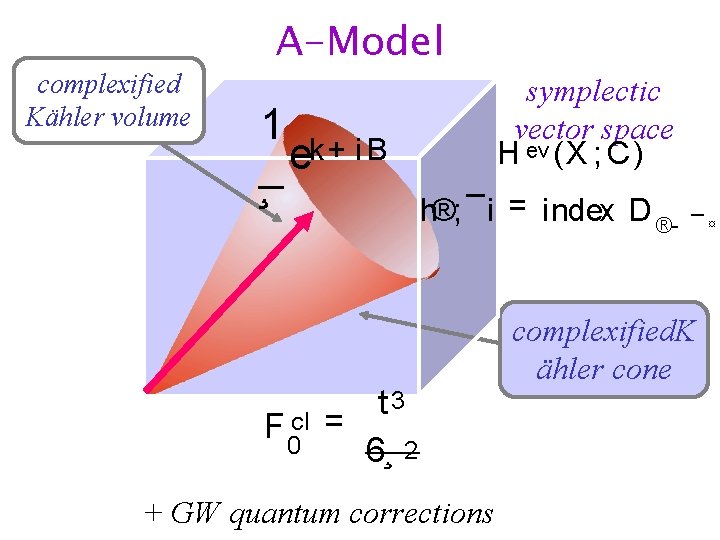
complexified Kähler volume A-Model 1 k+ i B e ¸ F 0 cl symplectic vector space H ev (X ; C ) h®; ¯i = index D ® t 3 = 6¸ 2 + GW quantum corrections ¯¤ complexified. K ähler cone

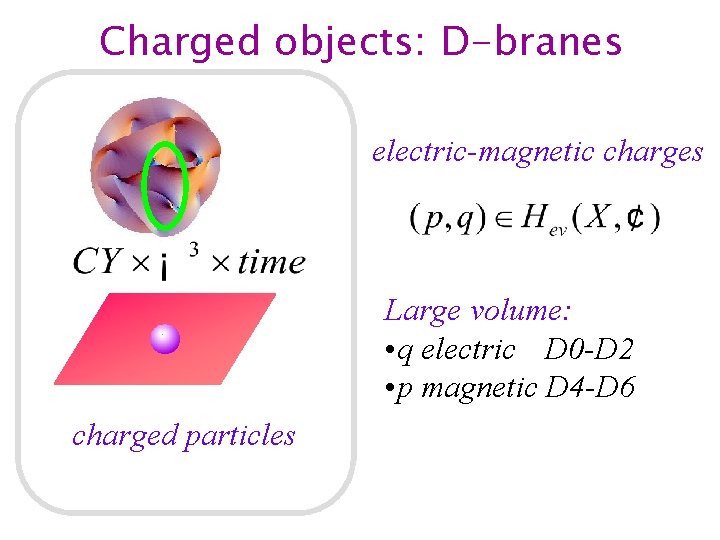
Charged objects: D-branes electric-magnetic charges Large volume: • q electric D 0 -D 2 • p magnetic D 4 -D 6 charged particles
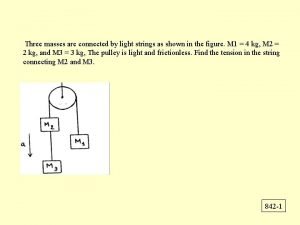
![Gauge Theory Invariants Coherent sheaf Charge E X ¹ E 2 K 0 Gauge Theory Invariants Coherent sheaf Charge E! X ¹ = [E] 2 K 0](https://slidetodoc.com/presentation_image_h2/f37b8ef1f91b1feab8835e2c414ce8ee/image-23.jpg)
Gauge Theory Invariants Coherent sheaf Charge E! X ¹ = [E] 2 K 0 (X ) = ¤ (conjectured) Donaldson-Thomas invariant R D(¹ ) = 1 [M ¹ ]v i r Moduli space of stable sheaves

Gauge Theory D( ) is conjectured to be the partition function of a 6 -dim topologically twisted gauge theory Z S= j. F j 2 + j. D Ái j 2 + [Ái ; Áj ]2 + : : : X Localizes to 6 -dim version of Hitchin’s equations

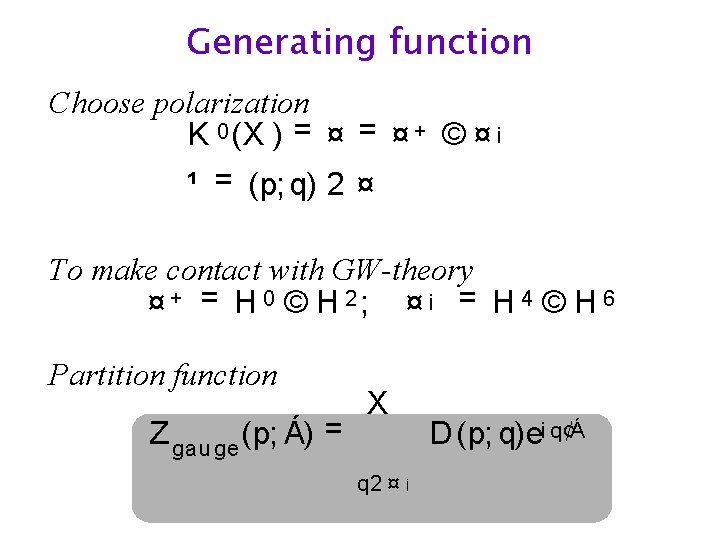
Generating function Choose polarization K 0 (X ) = ¤ + © ¤ ¡ ¹ = (p; q) 2 ¤ To make contact with GW-theory ¤ + = H 0 © H 2; ¤ ¡ = H 4 © H 6 Partition function Z gau ge (p; Á) = X q 2 ¤ ¡ D (p; q)ei q¢Á
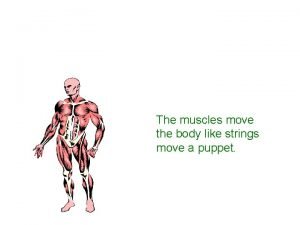
![GWDT Equivalence Maulik Nekrasov Okounkov Pandharipande Consider the case of rank one p GW-DT Equivalence [Maulik, Nekrasov, Okounkov, Pandharipande] Consider the case of rank one, p =](https://slidetodoc.com/presentation_image_h2/f37b8ef1f91b1feab8835e2c414ce8ee/image-26.jpg)
GW-DT Equivalence [Maulik, Nekrasov, Okounkov, Pandharipande] Consider the case of rank one, p = (1, 0) (ideal sheaves) Z gau ge (p; Á) = Z t op (t; ¸ ) where Á = (t; ¸ ) 2 H 2 (X ) © H 0 (X )

Donaldson-Thomas Invariants U(1) gauge theory + singularities q=(d, n) n = ch 3 » Tr F 3 d = ch 2 » Tr F 2 instanton strings Z gau ge = X d; n D (d; n)edt + n ¸

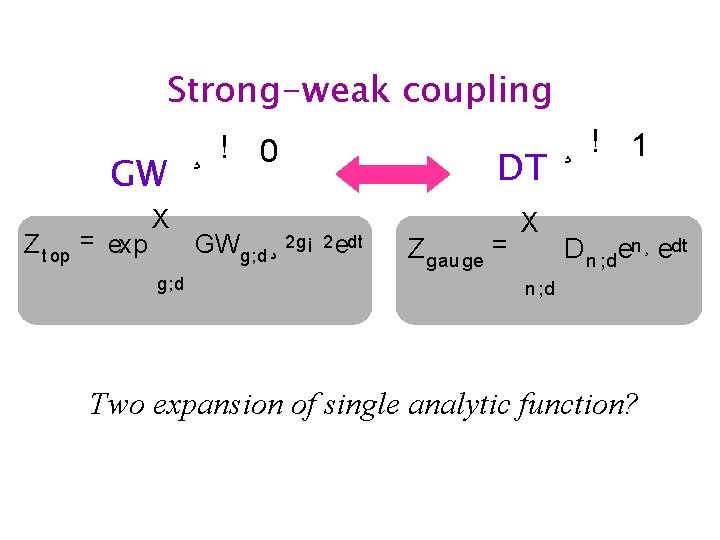
Strong-weak coupling GW Z t op = exp X g; d ¸ ! 0 GWg; d ¸ DT 2 g¡ 2 edt Z gau ge = X ¸ ! 1 D n ; d en ¸ edt n ; d Two expansion of single analytic function?

Gopakumar-Vafa invariants M-theory limit ¸ ¸ ! 1 virtual loops of M 2 branes

GV Partition function Gas of 5 d charged & spinning black holes Z (¸ ; t) = Y ³ 1 ¡ e¸ ( n 1 + n 2 + m ) + t d n 1 ; n 2 d ; m p GV-invariants (integers) N dm » d 3 ¡ m 2 Infinite products of Borcherds type. Automorphic properties? ´¡ N dm

Topological String Triality top. strings Gromov-Witten M-theory Gopakumar-Vafa gauge theory Donaldson-Thomas

Simplest Calabi-Yau

constant maps g

Stat-Mech: 3 d Partitions GW GV DT

Melting Crystals Okounkov, Reshetikhin, Vafa, Nekrasov, . . .
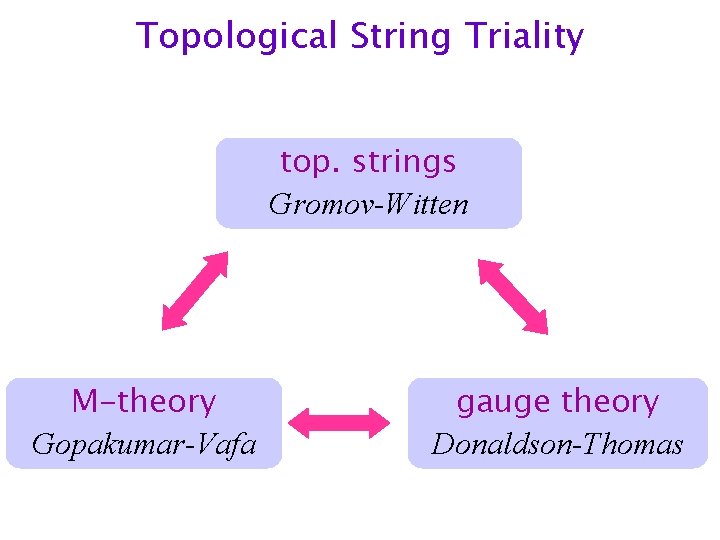
![OSV Conjecture Ooguri Strominger Vafa p 1 Consider the limit Z gau ge p OSV Conjecture [Ooguri, Strominger, Vafa] p! 1 Consider the limit Z gau ge (p;](https://slidetodoc.com/presentation_image_h2/f37b8ef1f91b1feab8835e2c414ce8ee/image-36.jpg)
OSV Conjecture [Ooguri, Strominger, Vafa] p! 1 Consider the limit Z gau ge (p; Á) » j. Z t op (t; ¸ )j 2 where µ p + iÁ = t 1 ; ¸ ¸ ¶ 2 H 2 (X ) © H 0 (X )

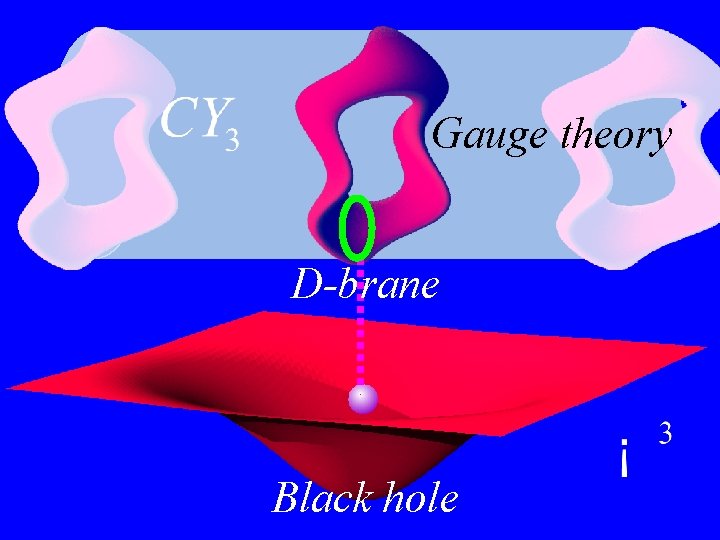
Gauge theory D-brane Black hole
![Black Hole Entropy semiclassical Bekenstein Hawking Black Hole Entropy (semi-classical) [Bekenstein, Hawking]](https://slidetodoc.com/presentation_image_h2/f37b8ef1f91b1feab8835e2c414ce8ee/image-38.jpg)
Black Hole Entropy (semi-classical) [Bekenstein, Hawking]

Microscopic counting (quantum) OSV S(p; q) = mi n Á f Im F t op (p + i Á) + qÁg

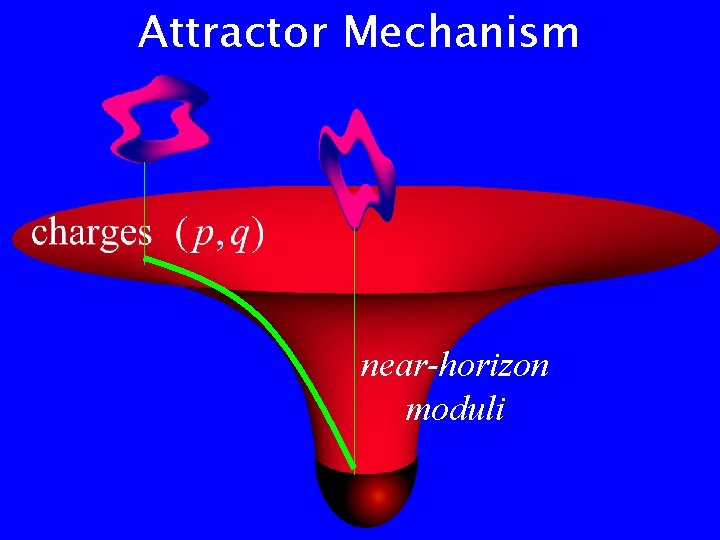
Attractor Mechanism near-horizon moduli

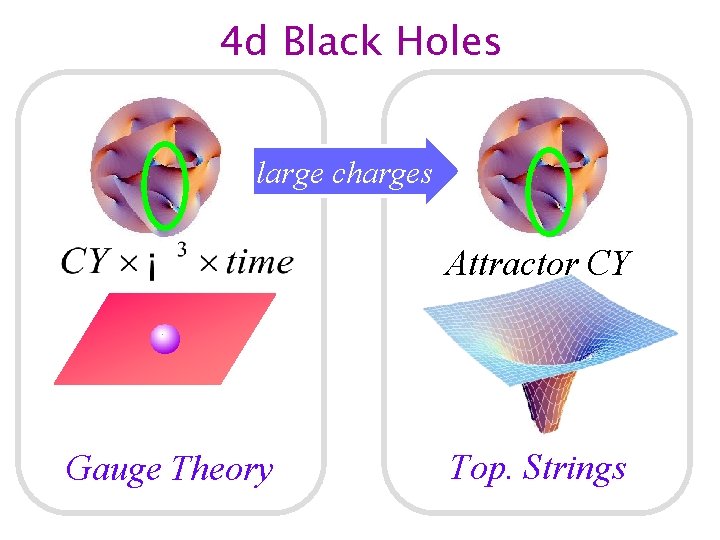
4 d Black Holes large charges Attractor CY Gauge Theory Top. Strings

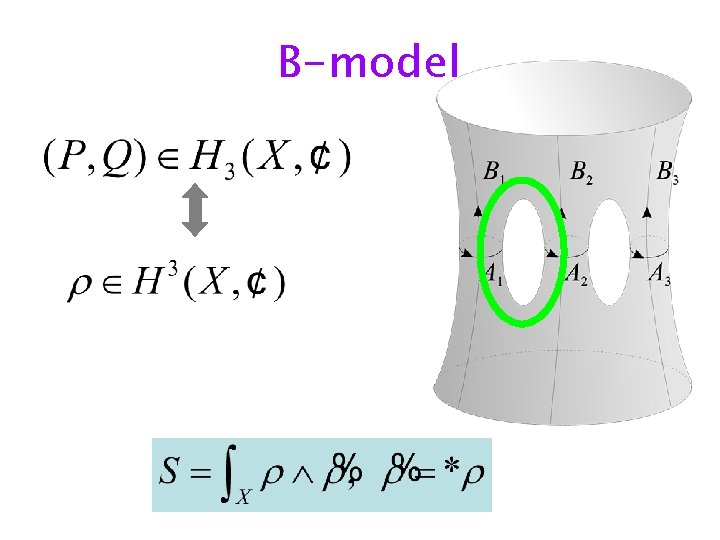
B-model

Hitchin’s theory of 3 -forms

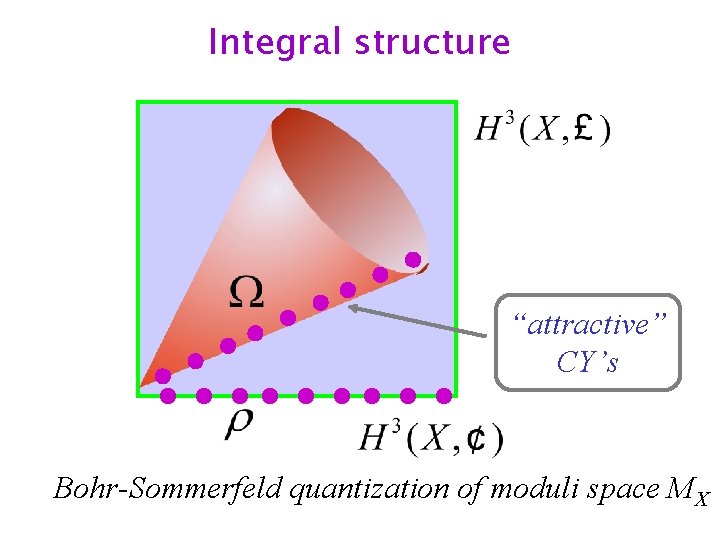
Integral structure “attractive” CY’s Bohr-Sommerfeld quantization of moduli space MX
![Example of OSV conjecture Local 2 torus in CY Vafa X area of T Example of OSV conjecture Local 2 -torus in CY [Vafa] X area of T](https://slidetodoc.com/presentation_image_h2/f37b8ef1f91b1feab8835e2c414ce8ee/image-45.jpg)
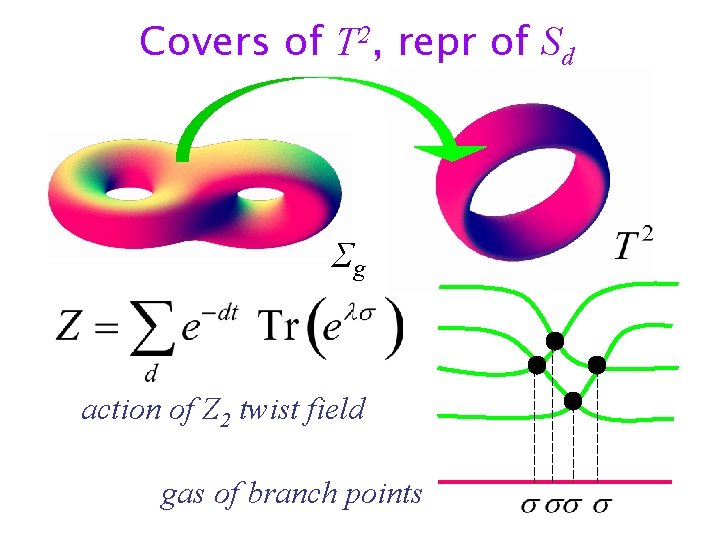
Example of OSV conjecture Local 2 -torus in CY [Vafa] X area of T 2 = t

Covers of T 2, repr of Sd Σg action of Z 2 twist field gas of branch points

Mirror symmetry: modular forms q = e 2¼i t

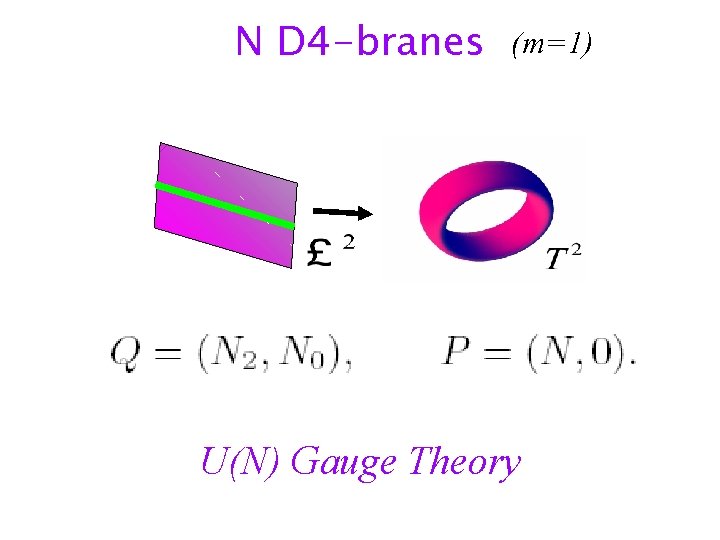
N D 4 -branes (m=1) U(N) Gauge Theory

Two-dimensional U(N) Yang-Mills
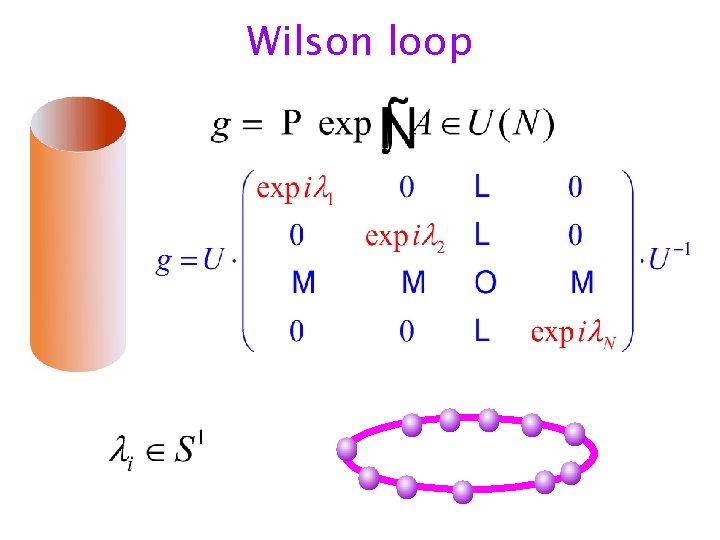
Wilson loop

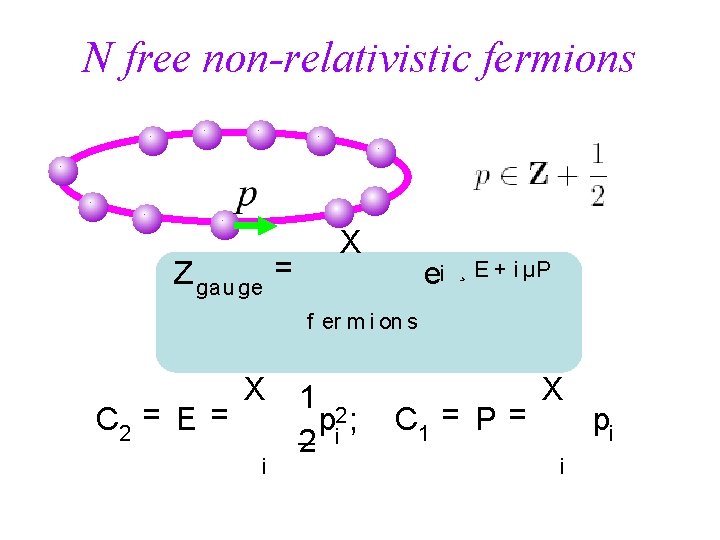
N free non-relativistic fermions Z gau ge = X e¡ ¸ E + i µP f er m i on s C 2 = E = X i 1 2 pi ; 2 C 1 = P = X i pi

Ground state energy E 0 = I m(F cl ) F cl 3 1 cl t t = + F 0 (t) + F 1 cl (t) = ¡ ¸ 2 6¸ 2 24

Black Hole states YM instantons Free fermion states

Hardy-Ramanuyan, Rademacher, Cardy Compute d(n) for large n? Modular invariance

Grand canonical partition function

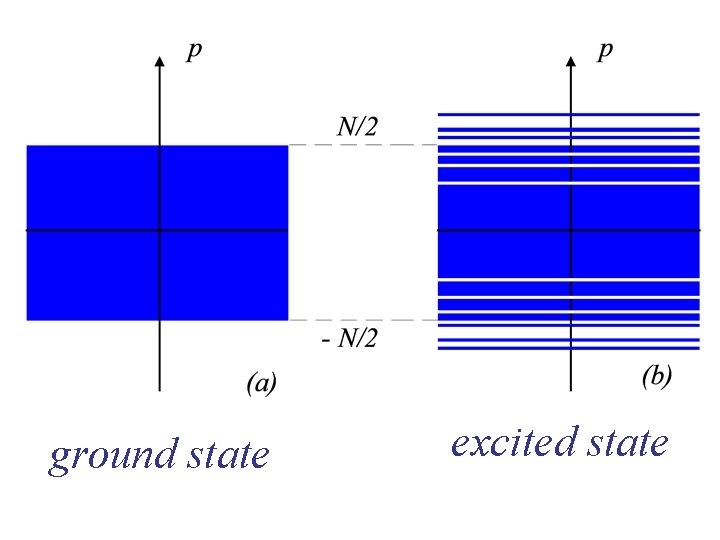
ground state excited state

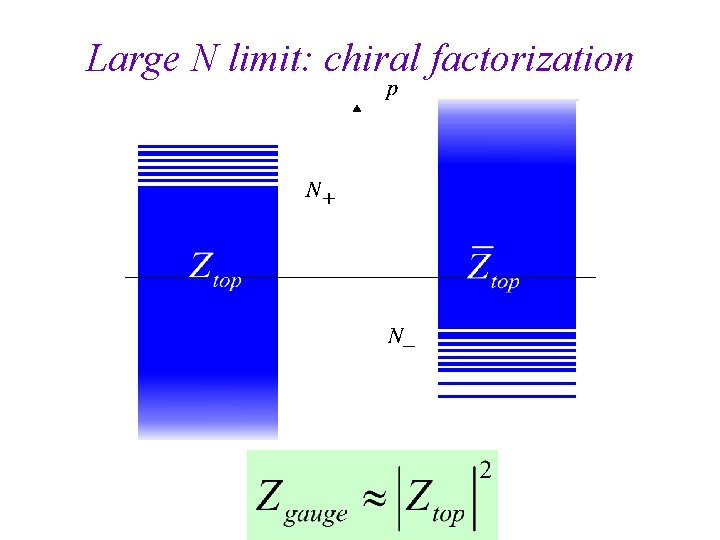
Large N limit: chiral factorization

Z t op (t; ¸ ) = I dx x Y p 2 Z ¸ = exp X 0 + ³ 1 + xept + ´ ³ 1 2 ¸ p 2 1 2 ¸ 2 g¡ 2 F g (t) g quasi-mdoular form of wt 6 g-6 1 + x ¡ 1 ept ¡ ´ 1 2 ¸ p 2

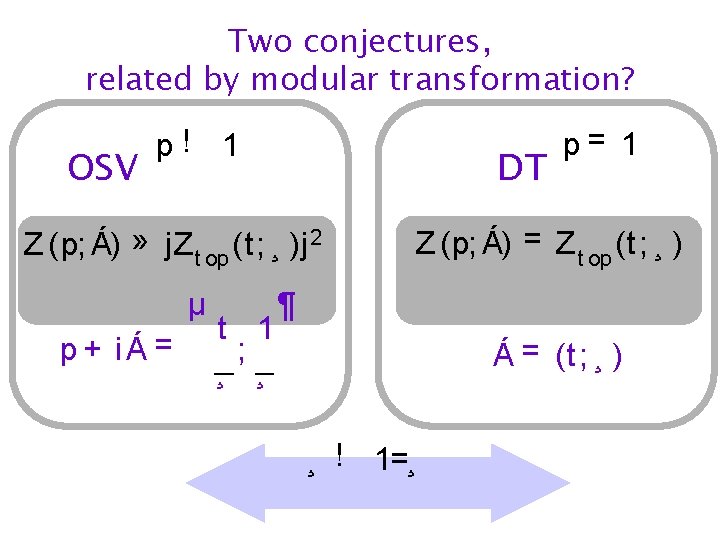
Two conjectures, related by modular transformation? OSV p! 1 DT Z (p; Á) » j. Z t op (t; ¸ )j 2 µ p + iÁ = t 1 ; ¸ ¸ p= 1 Z (p; Á) = Z t op (t; ¸ ) ¶ Á = (t; ¸ ) ¸ ! 1=¸
![Rank zero divisor P p 0 c 1 0 P Rank zero, divisor P p = (0; c 1 ) = (0; [P ])](https://slidetodoc.com/presentation_image_h2/f37b8ef1f91b1feab8835e2c414ce8ee/image-60.jpg)
Rank zero, divisor P p = (0; c 1 ) = (0; [P ]) Z gau ge CY X q = (ch 2 ; ch 3 ) = (d; n) elliptic genus of modulus space M P

Elliptic Genus If M is a CY k-fold elll(M ; z; ¿) S 1 -equivariant y-genus of the loop space LM weak Jacobi-form of wt 0 and index k/2 µ ¶ a¿ + b z k cz 2 ¼i = ; ell e 2 ( c ¿ + d ) ell(¿; z) c¿ + d ell(¿; z + m¿ + n) = e¡ ¼i d( m 2 ¿+ 2 m z) =2 ell(¿; z)

Elliptic Genus Fourier expansion X D (d; n)e 2¼i dz e 2¼i n ¿ elll(M ; z; ¿) = d; n Modular properties Z gau ge (t; ¸ ) = ell(M P ; t; ¸ )

Topological String Theory • Universal, deep, but mysterious object that captures many interesting connections between physics and geometry.

Happy Birthday, Nigel!
 Solids mechanics
Solids mechanics Topological band theory
Topological band theory Pf3 molecular geometry
Pf3 molecular geometry Gauge field theory
Gauge field theory 4 electron domains 2 lone pairs
4 electron domains 2 lone pairs This molecule is
This molecule is Ioi camp
Ioi camp Topological sorting definition
Topological sorting definition Topological sort calculator
Topological sort calculator Topological sort calculator
Topological sort calculator Image representation and description
Image representation and description Regional descriptors in image processing
Regional descriptors in image processing Topological sort uses
Topological sort uses Topological mott insulator
Topological mott insulator Topological sort online
Topological sort online Strongly connected components
Strongly connected components Topological sort pseudocode
Topological sort pseudocode Topological sort
Topological sort Topological sort bfs
Topological sort bfs Topological sort can be implemented by?
Topological sort can be implemented by? Topological sort can be implemented by?
Topological sort can be implemented by? Graph topological sort
Graph topological sort Kahn's algorithm python
Kahn's algorithm python Topological sort algorithm
Topological sort algorithm Topological sort
Topological sort Partial order relation
Partial order relation Topological sorting
Topological sorting Elementary graph
Elementary graph Elastic strings and springs
Elastic strings and springs Pointers and strings
Pointers and strings Strings and other things
Strings and other things Assembly array of strings
Assembly array of strings Strings in java
Strings in java Image search reverse
Image search reverse Rate of energy transfer by sinusoidal waves on strings
Rate of energy transfer by sinusoidal waves on strings Python compare strings
Python compare strings Clapper (musical instrument)
Clapper (musical instrument) Micheal league
Micheal league Mrs sprockett's strange machine
Mrs sprockett's strange machine A type of cipher that uses multiple alphabetic strings.
A type of cipher that uses multiple alphabetic strings. Cld 8086
Cld 8086 Achievement standards network
Achievement standards network Three masses are connected by strings
Three masses are connected by strings Notation for sequences
Notation for sequences Upx unpacker
Upx unpacker Language c string
Language c string Vortex strings
Vortex strings Muscle strings
Muscle strings What are strings in c
What are strings in c C array of structs
C array of structs Jmp
Jmp Uniform circular motion lab answer key
Uniform circular motion lab answer key Ottawa suzuki strings
Ottawa suzuki strings Permutations and combinations
Permutations and combinations Ida pro strings
Ida pro strings Ida strings
Ida strings Declare a two dimensional array of strings named chessboard
Declare a two dimensional array of strings named chessboard Bellows pressure gauge advantages and disadvantages
Bellows pressure gauge advantages and disadvantages Difference between bonded and unbonded strain gauge
Difference between bonded and unbonded strain gauge Profile projector
Profile projector : a device that converts one voltage to another
: a device that converts one voltage to another Tva rain gauge
Tva rain gauge Upd
Upd Sliding bevel diagram
Sliding bevel diagram Bear banger 12 gauge
Bear banger 12 gauge