Fundamentals from Real Analysis Ali Sekmen Ph D




































































- Slides: 82

Fundamentals from Real Analysis Ali Sekmen, Ph. D. 2 Professor and Department Chair Department of Computer Science College of Engineering Tennessee State University 1 st Annual Workshop on Data Sciences

Outline Spaces Normed Vector Space Banach Space Inner Product Space Hilbert Space Metric Space Topological Space Subspaces and their Properties Subspace Angles and Distances

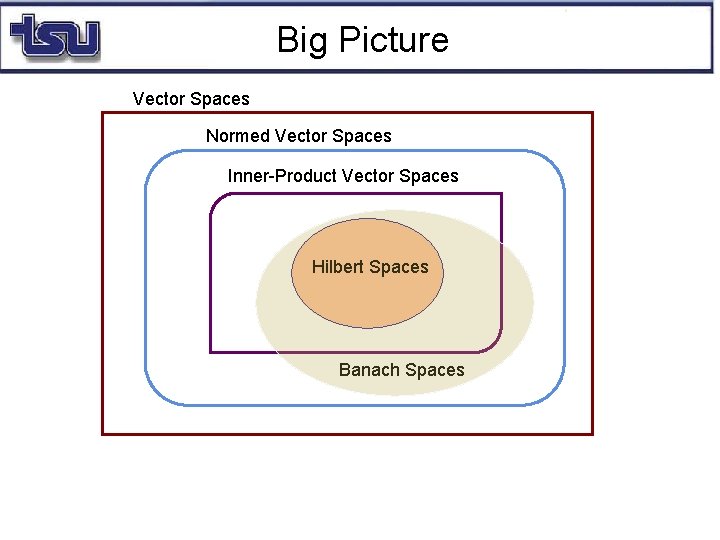
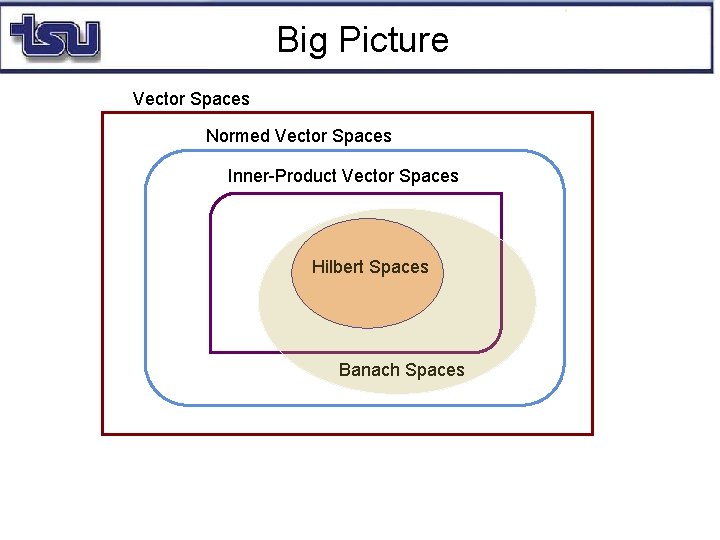
Big Picture Vector Spaces Normed Vector Spaces Inner-Product Vector Spaces Hilbert Spaces Banach Spaces

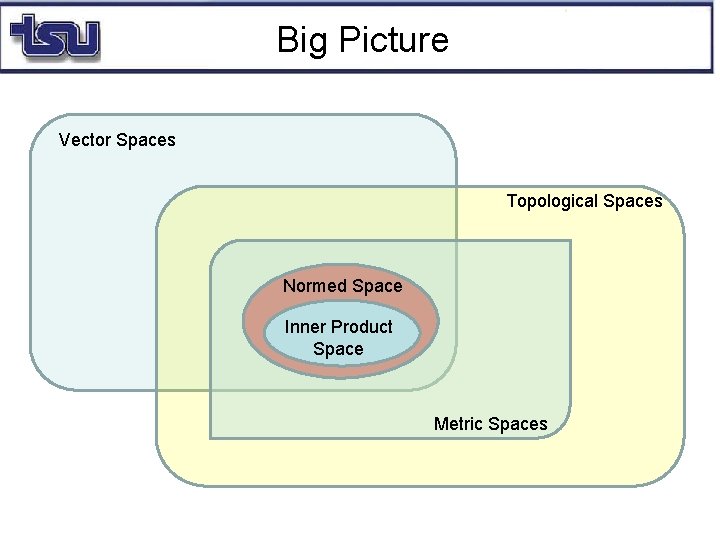
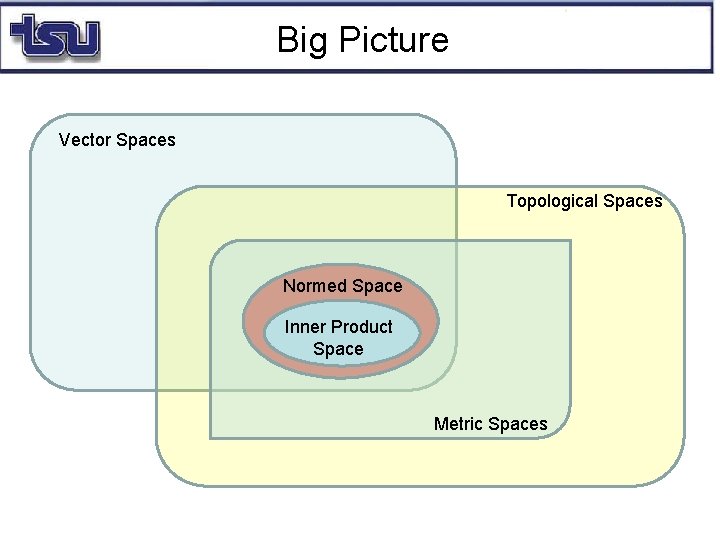
Big Picture Vector Spaces Topological Spaces Normed Space Inner Product Space Metric Spaces

What is a Vector Space? A vector space is a set of objects that may be added together or multiplied by numbers (called scalars) Scalars are typically real numbers But can be complex numbers, rational numbers, or generally any field Vector addition and scalar multiplication must satisfy certain requirements (called axioms)

What is a Vector Space? A vector space may have additional structures such as a norm or inner product This is typical for infinite dimensional function spaces whose vectors are functions Many practical problems require ability to decide whether a sequence of vectors converges to a given vector In order to allow proximity and continuity considerations, most vector spaces are endowed with a suitable topology A topology is a structure that allows to define “being close to each other” Such topological vector spaces have richer theory – Banach space topology is given by a norm – Hilbert space topology is given by an inner product

What is a Vector Space? Associativity Commutativity Identity Element Inverse Element Compatibility Distributivity Identity Element

Vector Spaces - Applications The Fourier transform is widely used in many areas of engineering and science We can analyze a signal in the time domain or in the frequency domain We can show that is a measure for the amount of the frequency s What does this have to do with vector spaces?

Vector Spaces - Example When we define the Fourier transform, we need to also define when the transform is well-defined The Fourier transform is defined on a vector space For the sake of simplicity, we are not considering equivalence classes of functions that are the same almost everywhere

Vector Spaces - Example What kind of functions have a Fourier series Periodic functions Let us say periodic functions We can have Fourier series of functions that belongs to the vector space If the function does not belong to this space, then the Fourier coefficients may not be well-defined

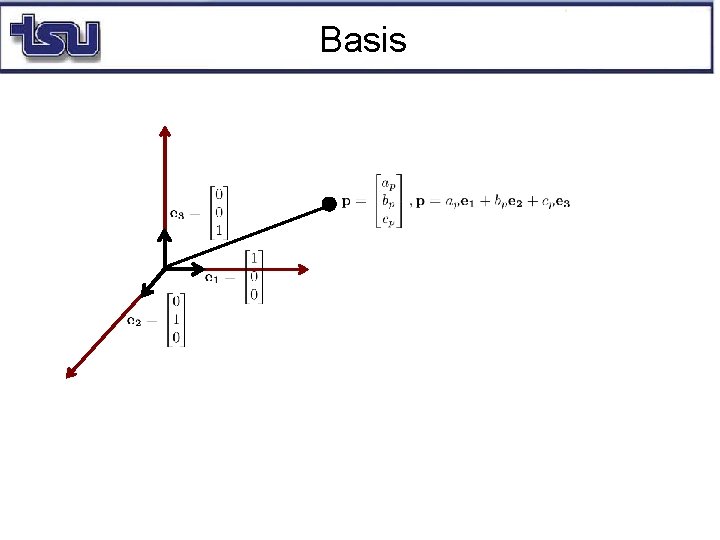
Basis Every vector space has a basis Every vector in a vector space can be written in a unique way as a finite linear combination of the elements in this basis # of elements in a basis is dimension of vector space

Basis

Vector Spaces - Example All of us know a very well-known vector space: For general vector spaces, we need a concept that corresponds to length in We use “norm” instead of “length”

Norm This concept is defined by mimicking what we know about

Euclidean Vector Norm

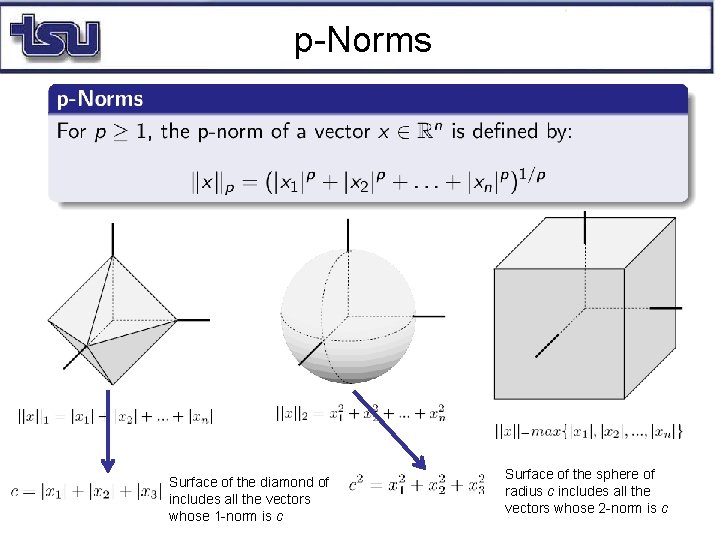
p-Norms Surface of the diamond of includes all the vectors whose 1 -norm is c Surface of the sphere of radius c includes all the vectors whose 2 -norm is c

Question Are there any vector spaces for which we cannot define any norms? Every finite dimensional real or complex topological vector space has a norm There are infinite dimensional topological vector spaces that do not have a norm that induces the topology

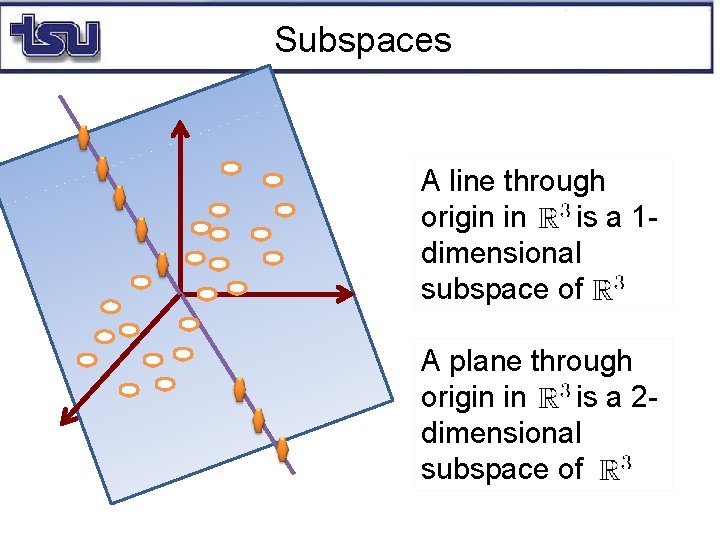
Subspaces Before we introduce some interesting vector spaces, we will now introduce “subspaces”

Subspaces A line through origin in is a 1 dimensional subspace of A plane through origin in is a 2 dimensional subspace of

Subspaces Consider trigonometric polynomials, i. e. , a finite linear combination of exponential functions We can show that trigonometric polynomials form a subspace of

Subspaces

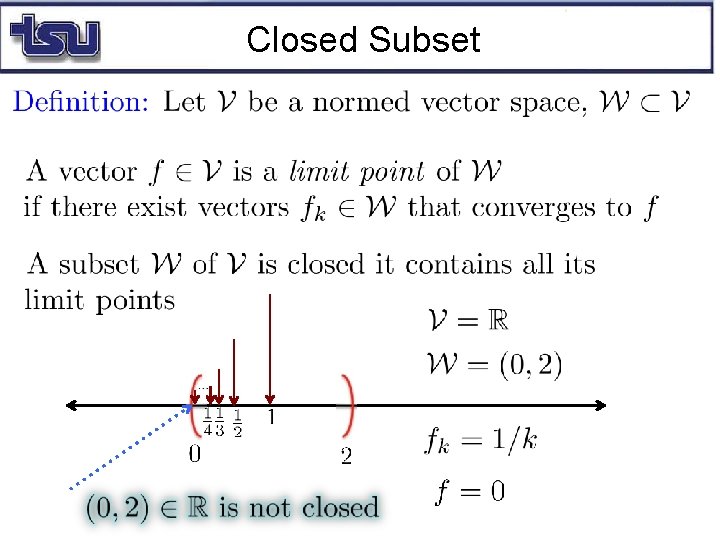
Closed Subset

A Vector Space

A Vector Space

A Vector Space

A Set of Polynomials

Set of Polynomials

Set of Polynomials

Set of Polynomials

Banach Space An important group of normed vector spaces in which a Cauchy sequence of vectors converges to an element of the space Banach spaces play an important role in functional analysis In many areas of analysis, the spaces are often Banach spaces

Convergence

Convergence

Convergence

Cauchy Sequences

Convergence and Cauchy

Banach Space

Banach Space



Inner Product for Inner product is a very important tool for analysis in. It is a measure of angle between vectors

General Inner Product

Example Inner Product Spaces

Cauchy-Schwarz Inequality

Important In any inner product vector space, regardless of the inner product we can always define a norm But opposite is not true. We may not always define an inner product from a given norm

Important We may define an inner product from a given norm if the parallelogram law holds for the norm In this case, the induced inner product from the norm is defined as

Hilbert Space A Hilbert space is a vector space equipped with an inner product such that when we consider the space with the corresponding induced norm, then that space is a Banach space

Hilbert Space

Big Picture Vector Spaces Normed Vector Spaces Inner-Product Vector Spaces Hilbert Spaces Banach Spaces

Metric Space

Topological Space Inner Product Spaces Angles Normed Vector Spaces Length Not as strong as angles Metric Spaces Distance Not as strong as length Topological Spaces What do we do if we do not have a notion of distance between elements? Nearness Not as strong as distance Via neighborhoods

Big Picture Vector Spaces Topological Spaces Normed Space Inner Product Space Metric Spaces

Subspaces (Revisited)

Sum of Subspaces

Union of Subspaces

More on Subspaces

More on Subspaces

Orthogonal Subspaces

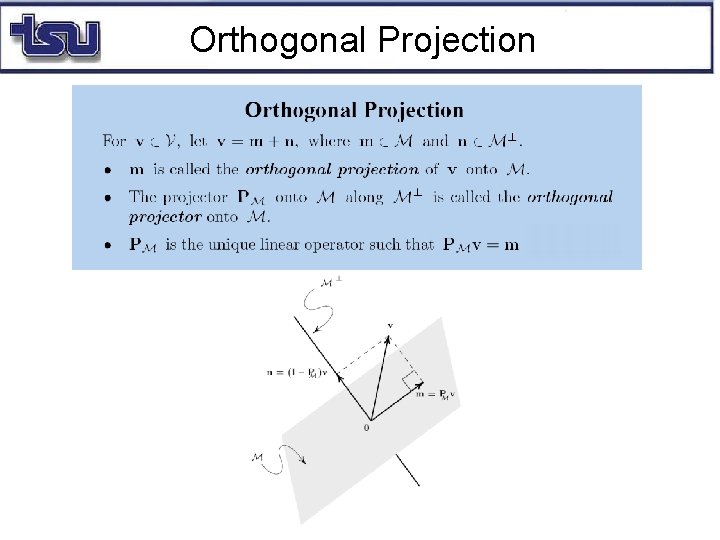
Orthogonal Projection

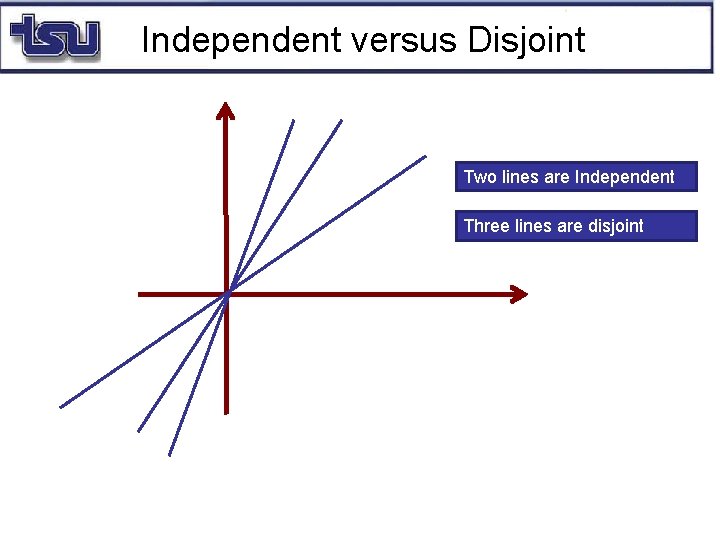
Independent versus Disjoint Two lines are Independent Three lines are disjoint

Independent versus Disjoint

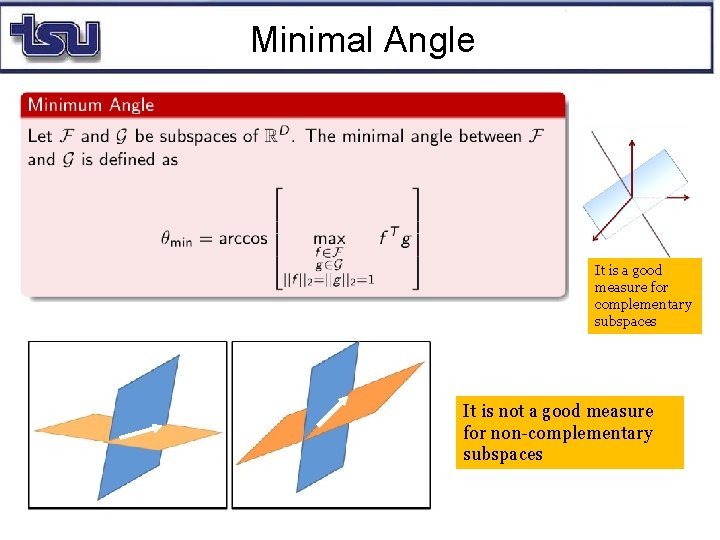
Minimal Angle It is a good measure for complementary subspaces It is not a good measure for non-complementary subspaces

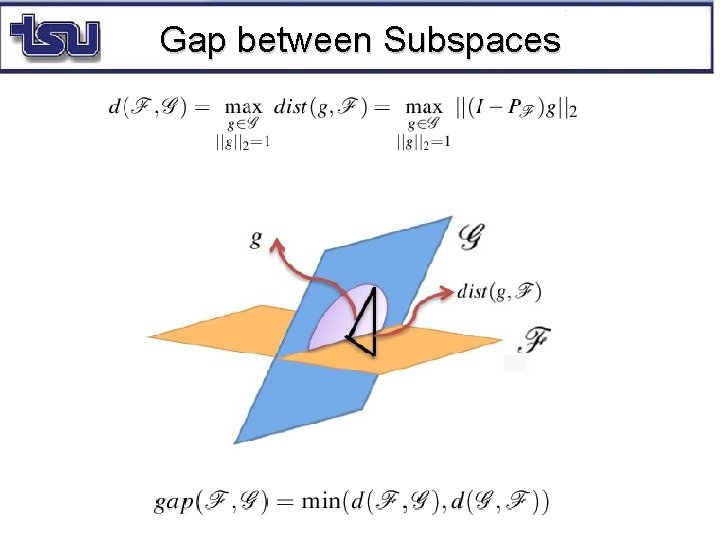
Gap between Subspaces

Maximum Angle It is useful for subspaces of equal dimension

Principle Angles

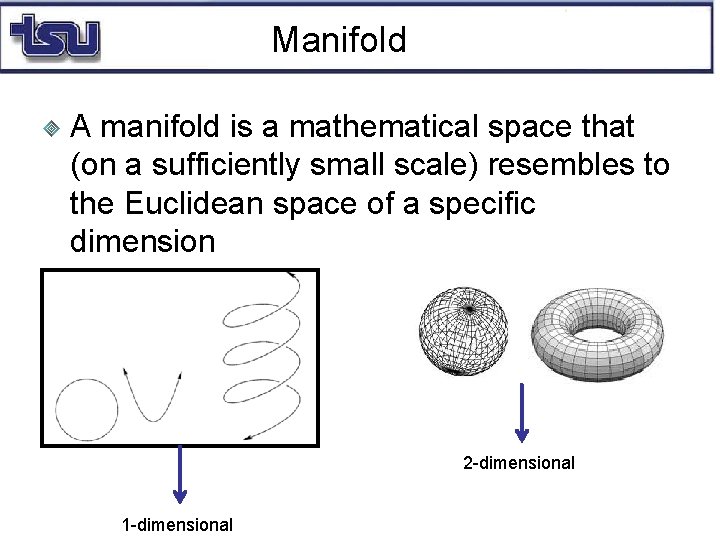
Manifold A manifold is a mathematical space that (on a sufficiently small scale) resembles to the Euclidean space of a specific dimension 2 -dimensional 1 -dimensional

Manifolds are like curves and surfaces, except that they might be of higher dimension Every manifold has a dimension The number of independent parameters to specify a point n dimensional manifold is an object modeled locally on It takes exactly n numbers to specify a point

Some References Functions, Spaces, and Expansions by Ole Christensen Topology by James Munkres


Topological Space

Topological Space

Metric Topology

Subspace Topology

Supremum

Supremum We do not only talk about sets but we also talk about functions Consider a function Range of the function

Supremum Sometimes supremum is attained, i. e. , we have a maximum value of the function

Supremum is attained Supremum is not attained

A Vector Space

Linear Mapping When we deal with finite dimensional spaces, we simply use the ideas from linear algebra However, when we deal with infinite dimensional spaces, we need to be careful

Linear Mapping

Linear Mapping

Linear Spaces

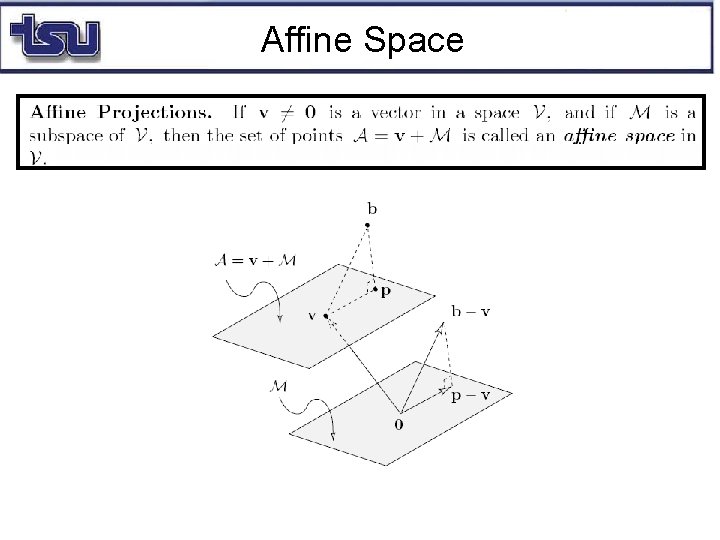
Affine Space
 Ali sekmen
Ali sekmen Ali sekmen
Ali sekmen Sezen sekmen
Sezen sekmen Real estate financial analysis
Real estate financial analysis Real estate finance fundamentals
Real estate finance fundamentals Fundamentals of analysis of algorithm efficiency
Fundamentals of analysis of algorithm efficiency Funcion de una variable real
Funcion de una variable real The real real fashion copywriter
The real real fashion copywriter Sensor and (tiempo real or real time)
Sensor and (tiempo real or real time) Real life problems polynomials
Real life problems polynomials Ch 9 ream people real choice case study
Ch 9 ream people real choice case study The real thing short story
The real thing short story Marketing real people real choices
Marketing real people real choices South pointe village apartments fishers in
South pointe village apartments fishers in Slidetodoc.com
Slidetodoc.com Marketing real people real decisions
Marketing real people real decisions Marketers classify innovations based on their
Marketers classify innovations based on their Prof dr ali hossain
Prof dr ali hossain Dede korkut'un torunu
Dede korkut'un torunu Rafayet ali
Rafayet ali Ali afzal malik
Ali afzal malik Nevjera ali umire
Nevjera ali umire Ali imran159
Ali imran159 The imamate in shia islam
The imamate in shia islam Tadbiri manozil asari
Tadbiri manozil asari Ya aliyu ya azeem meaning
Ya aliyu ya azeem meaning Ali darejeh
Ali darejeh Avolisyon
Avolisyon Kıssaların en güzeli
Kıssaların en güzeli On three days ali throws darts at a target
On three days ali throws darts at a target Spajanje ali sinteza
Spajanje ali sinteza Kanak-kanak pertama memeluk islam
Kanak-kanak pertama memeluk islam Dengesel koordinasyon testleri
Dengesel koordinasyon testleri Hz ali kadir gecesi
Hz ali kadir gecesi Mohammad ali javidian
Mohammad ali javidian Matematik doğanın dilidir
Matematik doğanın dilidir Ali osman alaca
Ali osman alaca Ali veríeis galantes pintados de preto e vermelho
Ali veríeis galantes pintados de preto e vermelho Mehmet ali uysal
Mehmet ali uysal Poesia al contrario
Poesia al contrario Hz eyyubun duasi
Hz eyyubun duasi Prof dr ali atan kimdir
Prof dr ali atan kimdir Alexandre mercier-dalphond
Alexandre mercier-dalphond Mehmet ali lahur
Mehmet ali lahur Voltair
Voltair Your name is ali khalid, isn't it
Your name is ali khalid, isn't it Ali pasha hotel
Ali pasha hotel Thomas carlyle imam ali
Thomas carlyle imam ali Ken goretta
Ken goretta Sobia ali
Sobia ali Mansa musa imperyo
Mansa musa imperyo Stožec oglišče
Stožec oglišče Ali madani md
Ali madani md Ziarat e mutlaqah 6
Ziarat e mutlaqah 6 Ali kuşçu
Ali kuşçu Dr ali saleh
Dr ali saleh Ali rezaei csulb
Ali rezaei csulb Mehmet ali ercan coğrafya
Mehmet ali ercan coğrafya Samir ould ali
Samir ould ali Database system concepts and architecture
Database system concepts and architecture Abrar ali saiyed
Abrar ali saiyed Climate emergency forum
Climate emergency forum Ali galip bayrak
Ali galip bayrak Ali sinir fəaliyyəti
Ali sinir fəaliyyəti Ali shahidi
Ali shahidi Ali hearn
Ali hearn Sukur ali khan
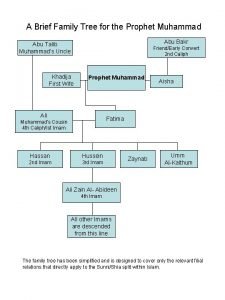
Sukur ali khan Prophet muhammad family tree sunni
Prophet muhammad family tree sunni Prestasi kabinet natsir dan sebab kejatuhannya
Prestasi kabinet natsir dan sebab kejatuhannya Anisa ali
Anisa ali How was sonni ali able to create such a wealthy kingdom?
How was sonni ali able to create such a wealthy kingdom? Ali şevki erek çok programlı anadolu lisesi
Ali şevki erek çok programlı anadolu lisesi Ali je sonce zvezda
Ali je sonce zvezda čista snov ali zmes
čista snov ali zmes Neviim nesta ali
Neviim nesta ali Ali sepahdari
Ali sepahdari Tanner testicular volume
Tanner testicular volume Ali ahmed is a mathematics professor who tries to involve
Ali ahmed is a mathematics professor who tries to involve Petas usm
Petas usm Ali parlayıcı
Ali parlayıcı Parlayıcı gazlar
Parlayıcı gazlar Ali parlayıcı
Ali parlayıcı Ters orantı grafiği
Ters orantı grafiği