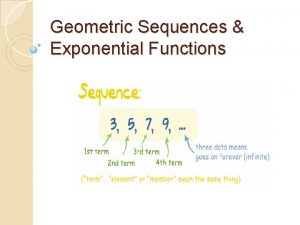
Function sequences 1 2 3 4 5 6

Pointwise convergence If for a function sequence at each or a function series the

Note that, in the last example, although the sequence functions are all continuous, the

A function sequence function converges uniformly to a on [a, b] if, for every

A function series function converges uniformly to a on [a, b] if, the sequence

Comparison of pointwise and uniform convergence In a pointwise convergence, the choice of the

Cauchy's test of uniform convergence Let a function sequence It converges uniformly to converge

Example The above sequence does not converge uniformly. To prove this we will apply

Let and m be an arbitrary index. Certainly, by letting x sufficiently close to

Uniform convergence of sequences and series conserves some of the properties of the individual

Let a sequence of functions continuous on [a, b] converge to a function f

Let a series of functions continuous on [a, b] converge to a function s

Let a sequence of functions integrable on [a, b] converge to a function f

Let a series a function f (x). Let is integrable and of functions integrable

If all the functions of a sequence or a series are differentiable on [a,

For the conservation of differentiation, only weaker theorems can be proved: Let be a

Let be a function series with every continuous derivative in [a, b]. Let one

Uniform convergence test for series (Weierstrass) Let If be a series of functions defined

Example The Weierstrass test can be used to prove the uniform convergence of the

Uniform convergence test for series (Dirichlet) A series uniformly converges in [a, b] if

Slides: 26

Download presentation

Function sequences 1 2 3 4 5 6 7 . . . set of all functions on (a, b) a b

Function sequence Function series

Pointwise convergence If for a function sequence at each or a function series the number sequence converges to or or number series , then we say that they converge pointwise in D. Thus pointwise convergence defines new functions We write and

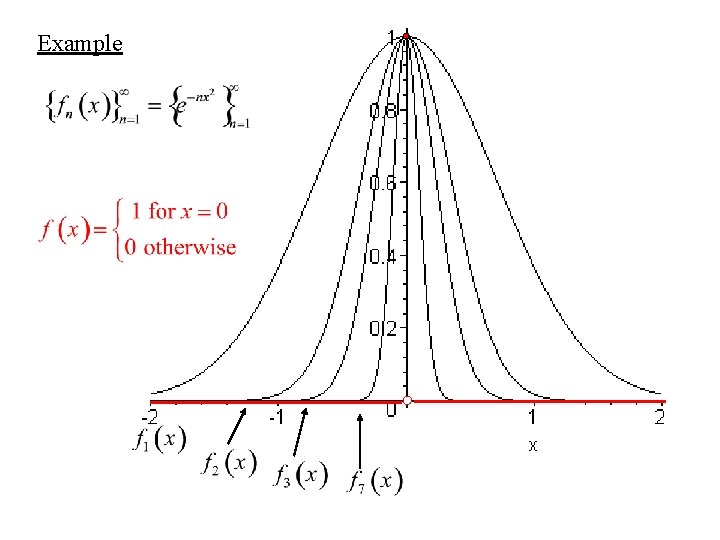
Example

Note that, in the last example, although the sequence functions are all continuous, the limit function is not. Thus pointwise convergence may define non-continuous using continuous ones. We shall examine such sequences of continuous functions that only produce continuous results.

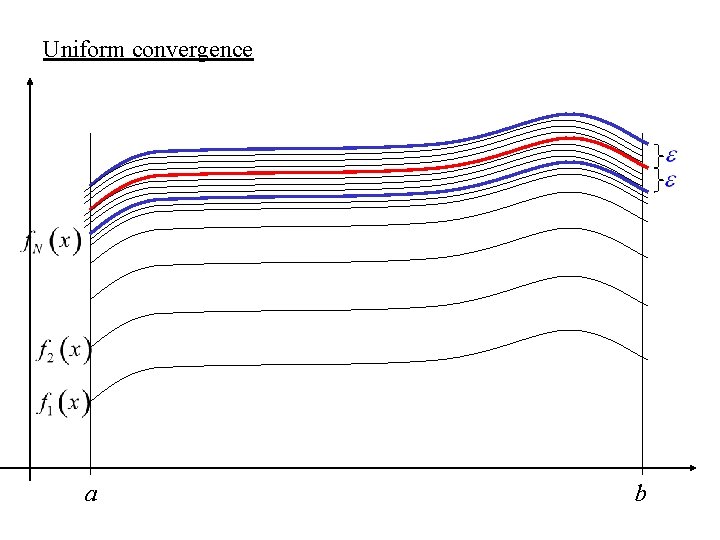
Uniform convergence a b

A function sequence function converges uniformly to a on [a, b] if, for every , there exists an index N such that, for every and for every , we have

A function series function converges uniformly to a on [a, b] if, the sequence of its partial sums converges uniformly to on [a, b].

Comparison of pointwise and uniform convergence In a pointwise convergence, the choice of the index N depends both on the point chosen in [a, b] and the and so we can write This might, for example result in the following: There might exist a sequence of points such that the sequence of indices is unbounded. With a uniform convergence, this cannot occur since for each there exists a uniform N regardless of the choice of

Cauchy's test of uniform convergence Let a function sequence It converges uniformly to converge to a function if and only if .

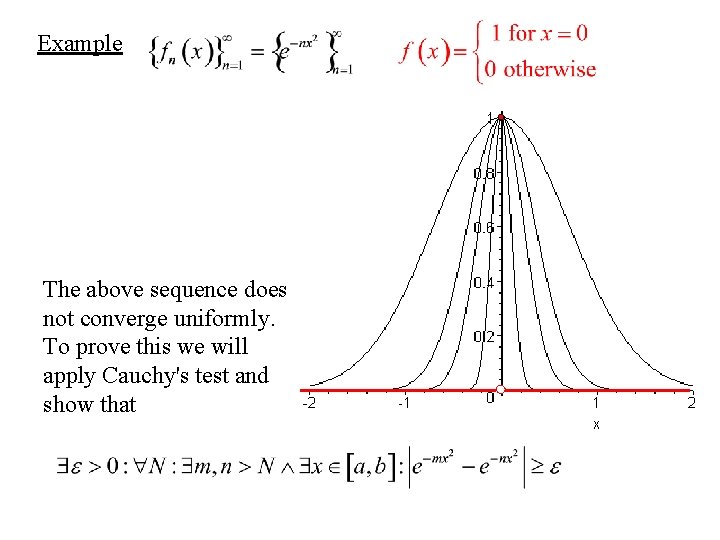
Example The above sequence does not converge uniformly. To prove this we will apply Cauchy's test and show that

Let and m be an arbitrary index. Certainly, by letting x sufficiently close to zero so that, say, x = x 0 , we will have On the other hand, it is clear that if we chose an index n > m sufficiently large we can "push this value down" so that Then of course we have

Uniform convergence of sequences and series conserves some of the properties of the individual functions such as continuity and integrability.

Let a sequence of functions continuous on [a, b] converge to a function f (x). Let Then f (x) is continuous. converge uniformly.

Let a series of functions continuous on [a, b] converge to a function s (x). Let Then s (x) is continuous. converge uniformly.

Let a sequence of functions integrable on [a, b] converge to a function f (x). Let Then f (x) is integrable and converge uniformly.

Let a series a function f (x). Let is integrable and of functions integrable on [a, b] converge to converge uniformly. Then f (x)

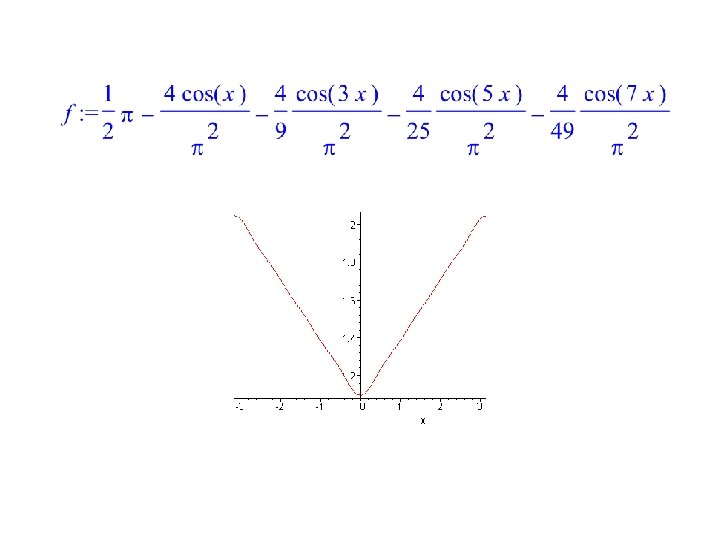
If all the functions of a sequence or a series are differentiable on [a, b], it does not necessarily mean that so is their limit or sum as the example below shows: The series has terms differentiable on and converges uniformly to the function y = |x|, which is not differentiable at x = 0. (next semester)

For the conservation of differentiation, only weaker theorems can be proved: Let be a function sequence with every continuous derivative in [a, b]. Let one point the limit converge at at least and let the sequence uniformly in [a, b]. Then having a converges uniformly in [a, b], of this sequence is differentiable in [a, b] and

Let be a function series with every continuous derivative in [a, b]. Let one point . converge at at least and let the sequence uniformly in [a, b]. Then having a converges uniformly in [a, b], is differentiable in [a, b] and

Uniform convergence test for series (Weierstrass) Let If be a series of functions defined on [a, b]. for every n and the number series converges, then uniformly converges.

Example The Weierstrass test can be used to prove the uniform convergence of the series from the previous example: Now the series in brackets is selected from the series whose convergence can be proved using, for example, the integral criterion.

Uniform convergence test for series (Dirichlet) A series uniformly converges in [a, b] if is a decreasing sequence converging to zero and if the partial sums of. are uniformly bounded, that is, if, for every and every n, we have where M > 0.