Sequences What is a sequence A sequence of

Sequences What is a sequence? A sequence of numbers is a list, an ordering that may or may not follow some rule. What are two types of Sequences? • Arithmetic Sequence: Is a sequence in which each term is equal to the previous term plus a constant. This constant is called the common difference. • Geometric Sequence: Is a sequence in which each term is equal to the previous term multiplied by a constant. This constant is called the common ratio.

When we are given a sequence and asked to find a specific term… 1. Determine whether the sequence is arithmetic or geometric. 2. Find the common difference (arithmetic) or the common ratio (geometric) 3. Use the appropriate formula to find the term asked for. Arithmetic Geometric

We will be reviewing arithmetic Find the common difference, find the indicated term, write the equation in both function and explicit form Let’s look at a sequence. 12, 6, 0, -6, . . . Find Write down every thing you need in the formula. n =10 because we are looking for the 10 th term d = -6 because we are adding -6 to each term = 12 because it is the first term of the sequence

Now use the information in the formula…don’t plug in “n” and you will have the explicit form This is the explicit form Distribute the -6 and simplify, change to f(n) and you will have function form This is function form To find the 10 th term use n = 10 and simplify

So let’s list some steps 1. First find the common difference 2. Next list all of the unknowns 3. Find the explicit form by plugging in the first term and the common difference 4. Find the function form by simplifying the explicit form 5. To find the specific term replace n with the term you are looking for.

You try… Find the common difference, the indicated term, write the explicit and function form of the sequence. 1. 6, 106, 206, 306, …n=15 2. -38, -45, -52, -59, …n=23 3. -16, 14, 44, 74, …n=52 1406 -206 1574

What is a recursive sequence? Definition: A recursive sequence is the process in which each step of a pattern is dependent on the step or steps before it. Recursion Formulas: A recursion formula defines the nth term of a sequence as a function of the previous term. If the first term of a sequence is known, then the recursion formula can be used to determine the remaining terms.

Sequence and Terms Let’s look at the following sequence Do you know what the rule is for the sequence? n² 1, 4, 9, 16, 25, 36, 49, …, The letter a with a subscript is used to represent function values of a sequence. The subscripts identify the location of a term.

How to read the subscripts: the prior term a term in the sequence the next term

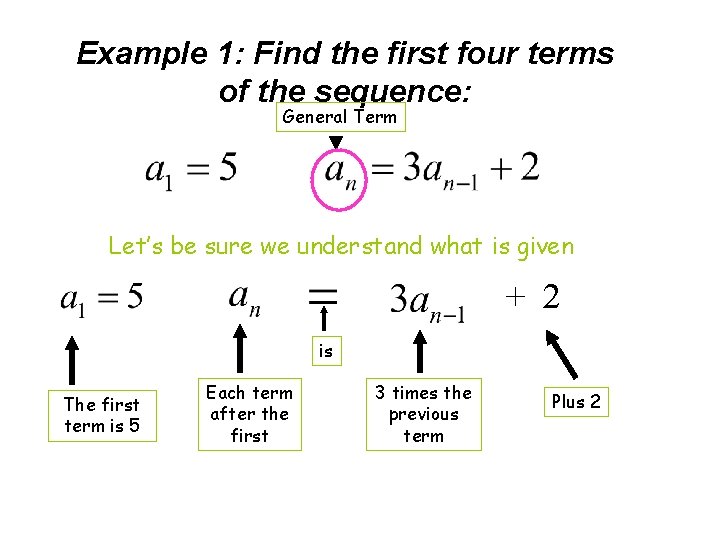
Example 1: Find the first four terms of the sequence: General Term Let’s be sure we understand what is given + 2 is The first term is 5 Each term after the first 3 times the previous term Plus 2

Continued… EX 1: Find the first four terms of the sequence: Start with general term for n>1 n=1 given n=2 n=3 n=4 Answer = 5, 17, 53, 161

Your turn: Ex 2: Find the next four terms of the sequence. Start with general term for n>1 n=1 given n=2 n=3 n=4 Answer = 3, 6, 12, 24

Write a recursive formula for the arithmetic sequence below. Step 1 : Make sure it is arithmetic Step 2 : Plug into the arithmetic recursive formula. Step 3 : Make sure you tell us what a 1 is equal to. Ex. 3 7, 3, -1, -5, -9, … The common difference = -4 The first term = 7

Last Example Choose the recursive formula for the given sequence. Answer = C