Arithmetic Sequences Geometric Sequences ADD To get next

Arithmetic Sequences Geometric Sequences • ADD To get next term • MULTIPLY to get next term • Have a common difference • Have a common ratio

In a geometric sequence, the ratio of any term to the previous term is constant. You keep multiplying by the SAME number each time to get the sequence. This same number is called the common ratio and is denoted by r What is the difference between an arithmetic sequence and a geometric sequence? Try to think of some geometric sequences on your own!

No common ratio! Geometric Sequence

To write a rule for the nth term of a geometric sequence, use the formula:

Write a rule for the nth term of the sequence 6, 24, 96, 384, . . Then find This is the general rule. It’s a formula to use to find any term of this sequence. To find , plug 7 in for n.

Write a rule for the nth term of the sequence 1, 6, 36, 216, 1296, . . Then find This is the general rule. It’s a formula to use to find any term of this sequence. To find , plug 8 in for n.

Write a rule for the nth term of the sequence 7, 14, 28, 56, 128, . . Then find

One term of a geometric sequence is = 3. Write a rule for the nth term. The common ratio is r

One term of a geometric sequence is and one term is Step 1: Find r -divide BIG small -find the distance between the two terms and take that root. Step 2: Find. Plug r, n, and equation. Then, solve for. into your Step 3: Write the equation using r and .

Write the rule when and .

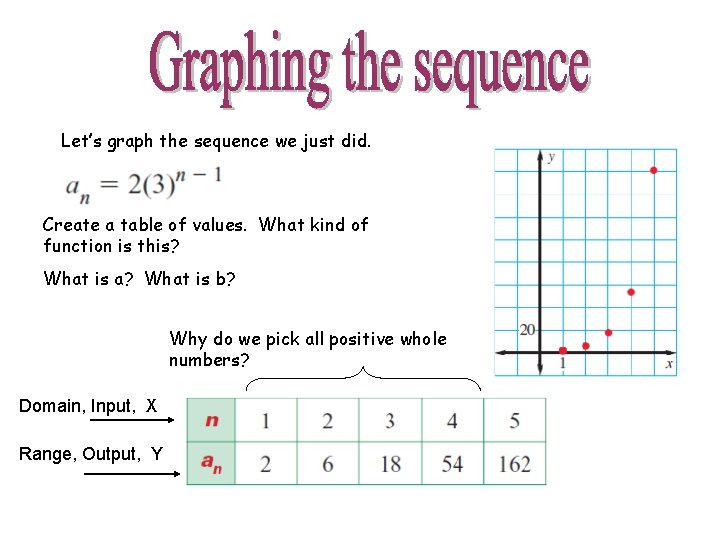
Let’s graph the sequence we just did. Create a table of values. What kind of function is this? What is a? What is b? Why do we pick all positive whole numbers? Domain, Input, X Range, Output, Y