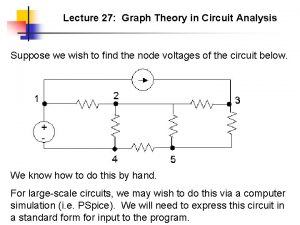
Extremal graph theory and limits of graphs Lszl

Extremal graph theory and limits of graphs László Lovász September 2012 1

Some old and new results from extremal graph theory Turán’s Theorem (special case proved by Mantel): G contains no triangles #edges n 2/4 Extremal: Theorem (Goodman): September 2012 2

Some old and new results from extremal graph theory Kruskal-Katona Theorem (very special case): k September 2012 n 3

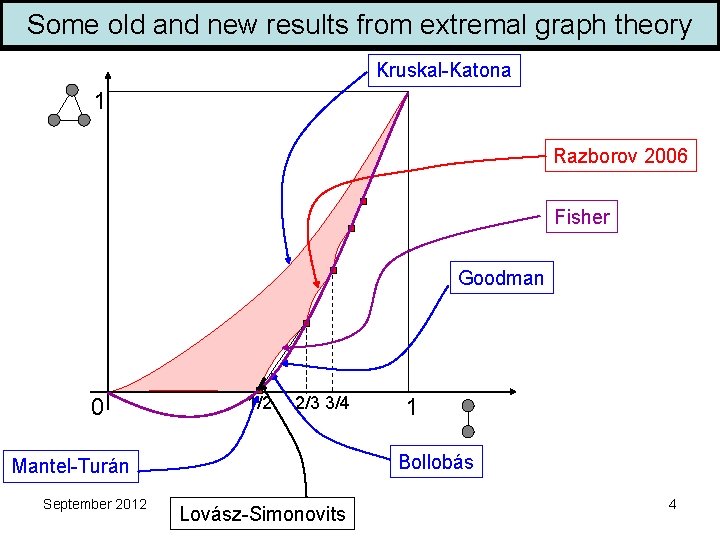
Semidefiniteness and new extremal graph theory Some old and results from Trickytheory examples extremal graph Kruskal-Katona 1 Razborov 2006 Fisher Goodman 0 1/2 2/3 3/4 Bollobás Mantel-Turán September 2012 1 Lovász-Simonovits 4

Some old and new results from extremal graph theory Theorem (Erdős): G contains no 4 -cycles #edges n 3/2/2 (Extremal: conjugacy graph of finite projective planes) September 2012 5

Some old and new results from extremal graph theory Theorem (Erdős-Stone-Simonovits): (F)=3 September 2012 6

General questions about extremal graphs -Which inequalities between subgraph densities are valid? - Can all valid inequalities be proved using just Cauchy-Schwarz? - Is there always an extremal graph? - Which graphs are extremal? September 2012 7

General questions about extremal graphs -Which inequalities between subgraph densities are valid? - Can all valid inequalities be proved using just Cauchy-Schwarz? - Is there always an extremal graph? - Which graphs are extremal? September 2012 8

Homomorphism functions Homomorphism: adjacency-preserving map Probability that random map V(F) V(G) is a hom If valid for large G, then valid for all September 2012 9

General questions about extremal graphs -Which inequalities between subgraph densities are valid? - Can all valid inequalities be proved using just Cauchy-Schwarz? - Is there always an extremal graph? - Which graphs are extremal? September 2012 10

Which inequalities between densities are valid? Undecidable… Hatami-Norine September 2012 11

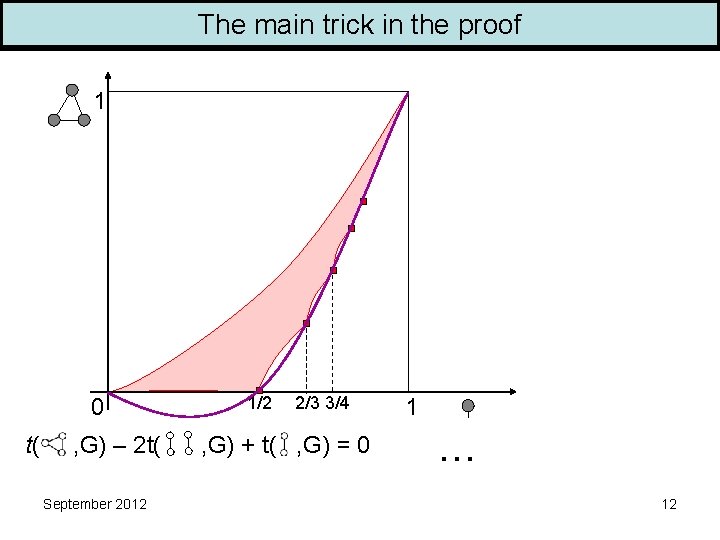
The main trick in the proof 1 0 t( , G) – 2 t( September 2012 1/2 2/3 3/4 , G) + t( , G) = 0 1 … 12

Which inequalities between densities are valid? Undecidable… Hatami-Norine …but decidable with an arbitrarily small error. L-Szegedy September 2012 13

General questions about extremal graphs -Which inequalities between subgraph densities are valid? - Can all valid inequalities be proved using just Cauchy-Schwarz? - Is there always an extremal graph? - Which graphs are extremal? September 2012 14

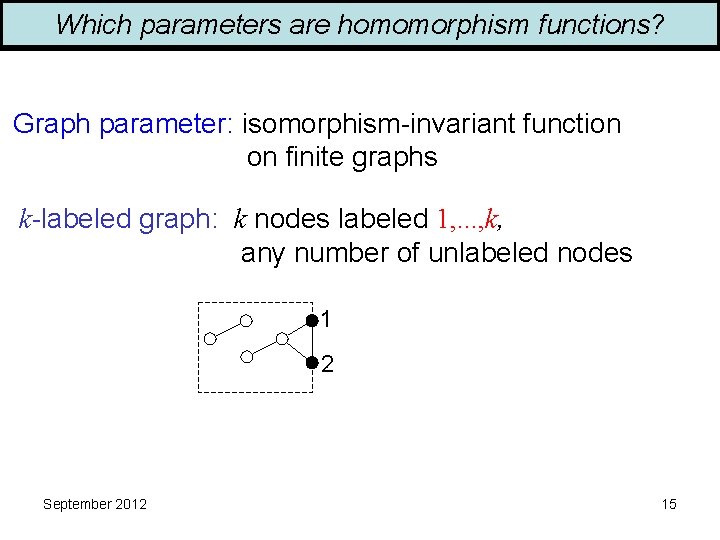
Which parameters are homomorphism functions? Graph parameter: isomorphism-invariant function on finite graphs k-labeled graph: k nodes labeled 1, . . . , k, any number of unlabeled nodes 1 2 September 2012 15

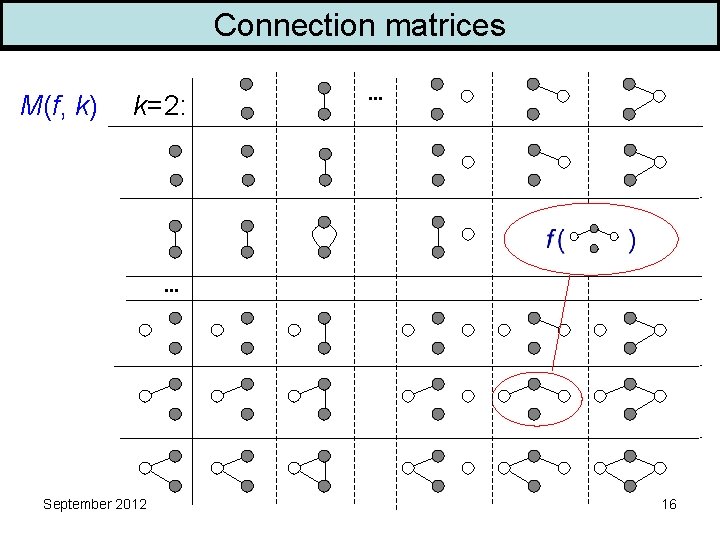
Connection matrices M(f, k) k=2: . . . September 2012 16

Which parameters are homomorphism functions? f = hom(. , H) for some weighted graph H M(f, k) is positive semidefinite and has rank ck Freedman - L - Schrijver September 2012 17

Computing with graphs k-labeled quantum graph: 1 finite formal sum of k-labeled graphs 2 Gk = {k-labeled quantum graphs} infinite dimensional linear space September 2012 18

Computing with graphs Define products: G 1, G 2: k-labeled graphs G 1 G 2 = G 1 G 2, labeled nodes identified is a commutative algebra with unit element September 2012 . . . 19

Computing with graphs Inner product: f: graph parameter extend linearly September 2012 20

Computing with graphs f is reflection positive September 2012 21

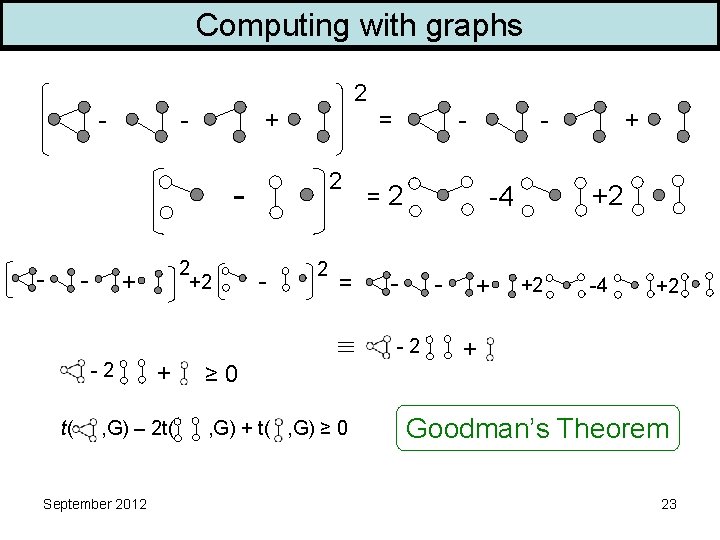
Computing with graphs Write x ≥ 0 if hom(x, G) ≥ 0 for every graph G. Turán: -2 + Kruskal-Katona: Blakley-Roy: September 2012 - - 22

Computing with graphs 2 - - + = 2 - - 2 +2 + - 2 = -2 t( + , G) – 2 t( September 2012 ≥ 0 , G) + t( , G) ≥ 0 - - =2 +2 -4 - - -2 + + +2 -4 +2 + Goodman’s Theorem 23

Positivstellensatz for graphs? If a quantum graph x is sum of squares (ignoring labels and isolated nodes), then x ≥ 0. Question: Suppose that x ≥ 0. Does it follow that No! Hatami-Norine September 2012 24

A weak Positivstellensatz Let x be a quantum graph. Then x 0 L-Szegedy September 2012 25

Proof of the weak Positivstellensatz (sketch 2) the optimum of a semidefinite program is 0: minimize subject to M(f, k) positive semidefinite for all k f(K 1)=1 f(G K 1)=f(G) Apply Duality Theorem of semidefinite programming September 2012 26

General questions about extremal graphs -Which inequalities between subgraph densities are valid? - Can all valid inequalities be proved using just Cauchy-Schwarz? - Is there always an extremal graph? - Which graphs are extremal? September 2012 27

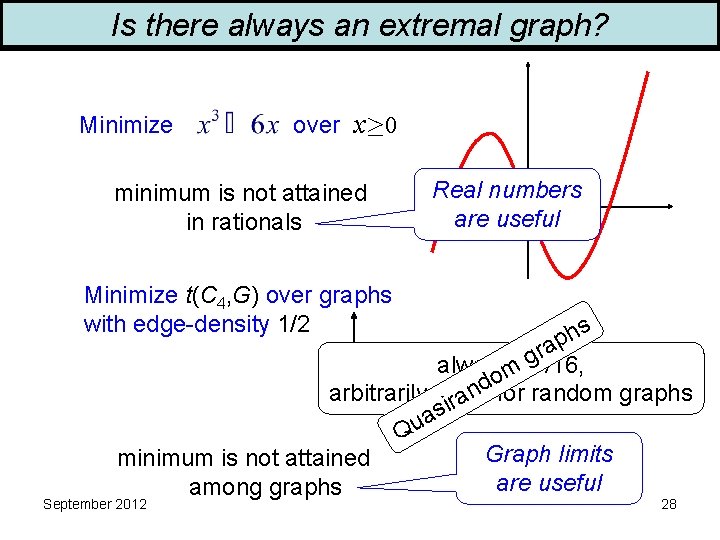
Is there always an extremal graph? Minimize over x 0 minimum is not attained in rationals Real numbers are useful Minimize t(C 4, G) over graphs with edge-density 1/2 s h p a r g alwaysm>1/16, o d n arbitrarily close a for random graphs r i as u Q Graph limits minimum is not attained are useful among graphs September 2012 28

Limit objects (graphons) September 2012 29

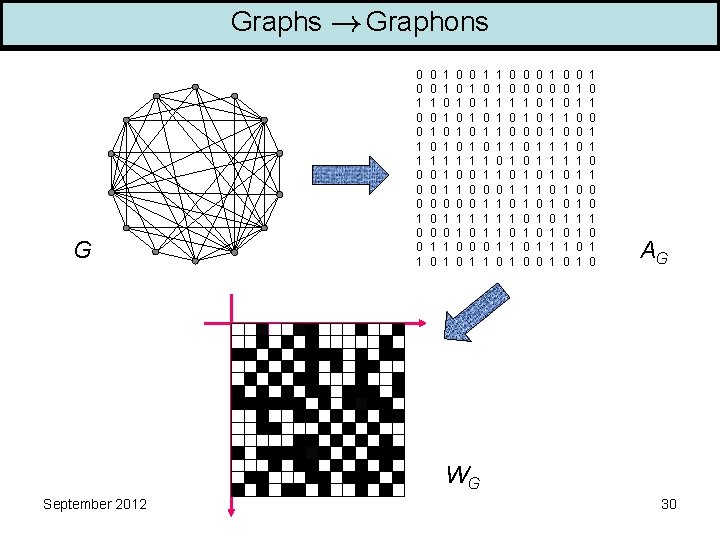
Graphs Graphons G 0 0 1 1 0 0 0 1 0 1 0 0 0 1 0 1 1 1 1 0 0 1 0 1 0 1 1 0 0 0 1 1 0 1 0 1 1 1 1 0 0 0 1 1 0 1 0 1 1 0 0 0 1 1 1 0 0 0 0 1 1 0 1 0 1 0 1 1 1 0 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 0 0 1 0 AG WG September 2012 30

Limit objects (graphons) t(F, WG)=t(F, G) (G 1, G 2, …) convergent: F t(F, Gn) converges September 2012 31

Limit objects For every convergent graph sequence (Gn) there is a graphon W such that Gn W. LS For every graphon W there is a graph sequence (Gn) such that Gn W. LS W is essentially unique (up to measure-preserving transformation). BCL September 2012 32

Is there always an extremal graph? No, but there is always an extremal graphon. The space of graphons is compact. September 2012 33

Semidefinite connection matrices f: graph parameter f = t(. , W) k M(f, k) is positive semidefinite, f( )=1 and f is multiplicative September 2012 34

General questions about extremal graphs -Which inequalities between subgraph densities are valid? - Can all valid inequalities be proved using just Cauchy-Schwarz? - Is there always an extremal graph? - Which graphs are extremal? September 2012 35

Extremal graphon problem Given quantum graphs g 0, g 1, …, gm, find max t(g 0, W) subject to t(g 1, W) = 0 … t(gm, W) = 0 September 2012 36

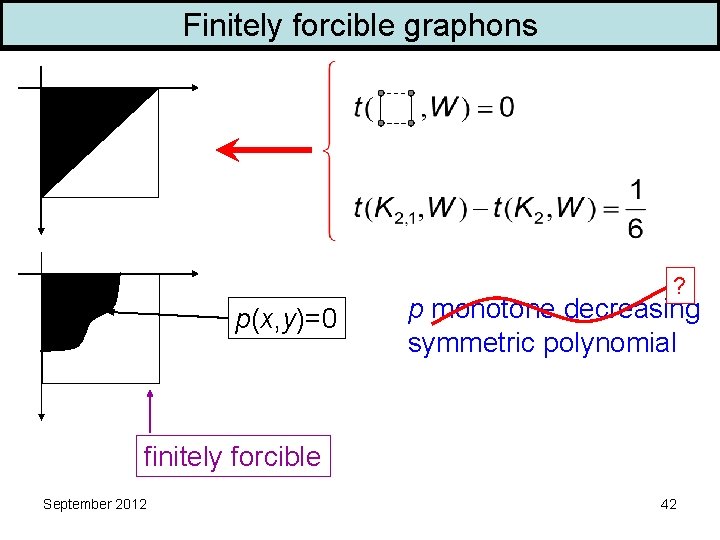
Finite forcing Finitely forcible graphons Graphon W is finitely forcible: Every finitely forcible graphon is extremal: minimize Every unique extremal graphon is finitely forcible. ? ? Every extremal graph problem has a finitely forcible extremal graphon ? ? September 2012 37

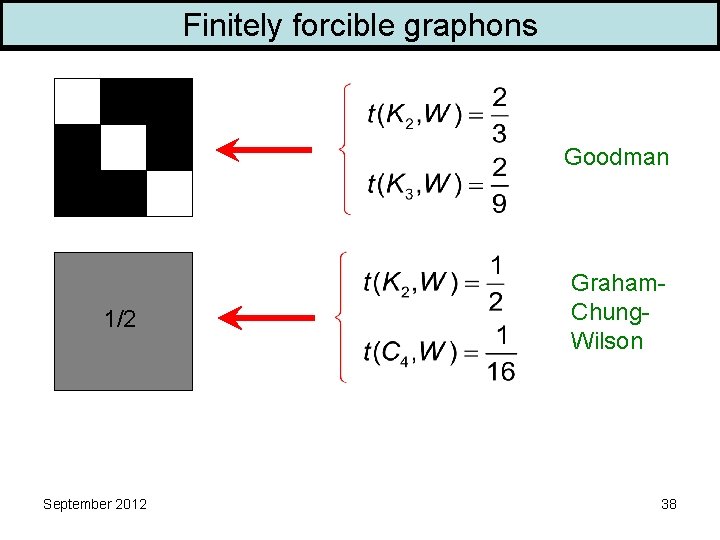
Finitely forcible graphons Goodman 1/2 September 2012 Graham. Chung. Wilson 38

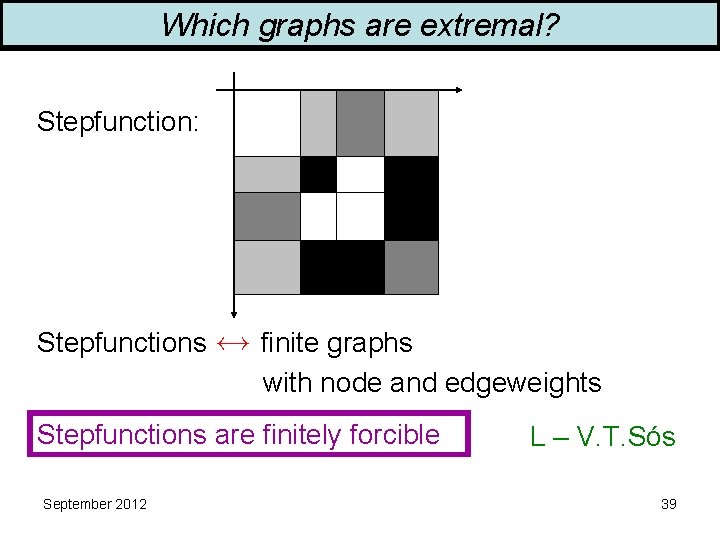
Which graphs are extremal? Stepfunction: Stepfunctions finite graphs with node and edgeweights Stepfunctions are finitely forcible September 2012 L – V. T. Sós 39

Finitely expressible properties d-regular graphon: d-regular September 2012 40

Finitely expressible properties W is 0 -1 valued, and can be rearranged to be monotone decreasing in both variables "W is 0 -1 valued" is not finitely expressible in terms of simple gaphs. W is 0 -1 valued September 2012 41

Finitely forcible graphons ? p(x, y)=0 p monotone decreasing symmetric polynomial finitely forcible September 2012 42

Finitely forcible graphons S p(x, y)=0 Stokes September 2012 43

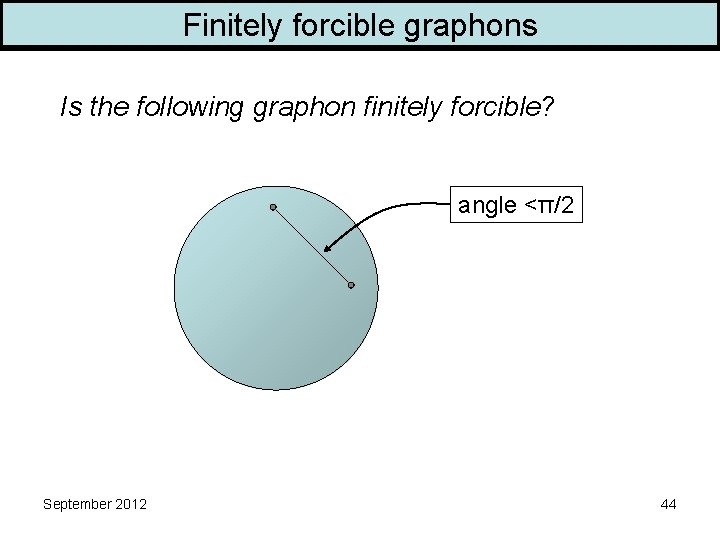
Finitely forcible graphons Is the following graphon finitely forcible? angle <π/2 September 2012 44

The Simonovits-Sidorenko Conjecture F bipartite, G arbitrary t(F, G) ≥ t(K 2, G)|E(F)| Known when September 2012 ? F is a tree, cycle, complete bipartite… Sidorenko F is hypercube Hatami F has a node connected to all nodes in the other color class Conlon, Fox, Sudakov F is "composable" Li, Szegedy 45

The Simonovits-Sidorenko Conjecture Two extremal problems in one: For fixed G and |E(F)|, t(F, G) is minimized by F= … For fixed F and t( , G), t(F, G) is minimized by random G September 2012 asymptotically 46

The integral version Let W W 0, W≥ 0, ∫W=1. Let F be bipartite. Then t(F, W)≥ 1. ? For fixed F, t(F, W) is minimized over W≥ 0, ∫W=1 by W 1 September 2012 47

The local version Let Then t(F, W) 1. September 2012 48

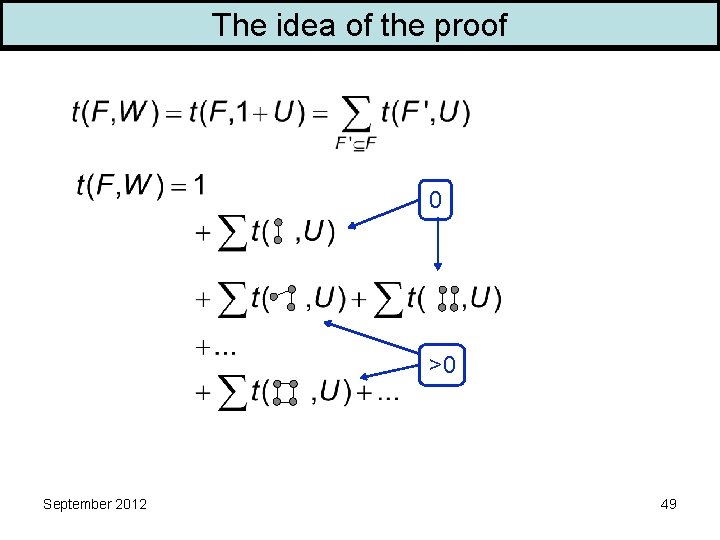
The idea of the proof 0 0< September 2012 49

The idea of the proof Main Lemma: If -1≤ U ≤ 1, shortest cycle in F is C 2 r, then t(F, U) ≤ t(C 2 r, U). September 2012 50

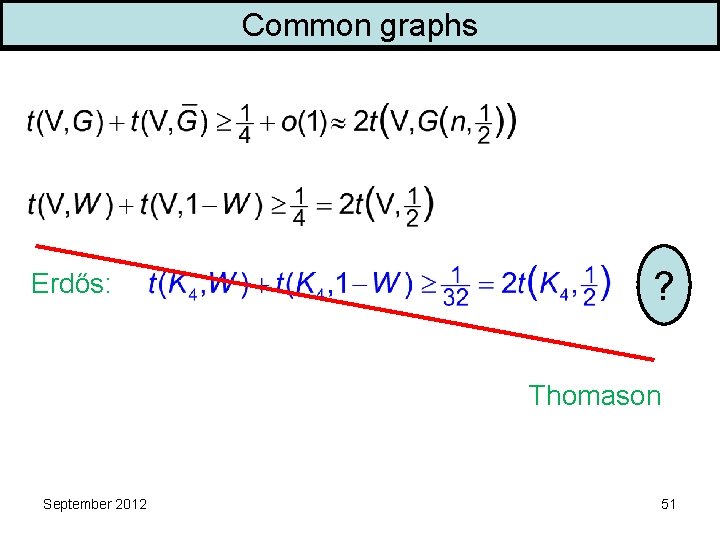
Common graphs Erdős: ? Thomason September 2012 51

Common graphs Hatami, Hladky, Kral, Norine, Razborov F common: Common graphs: Non-common graphs: Sidorenko graphs (bipartite? ) graph containing September 2012 Jagger, Stovícek, Thomason 52

Common graphs September 2012 53

Common graphs F common: is common. 8 +2 + =4 +2 September 2012 Franek-Rödl +4 +( +2 )2 +4( - ) 54

Common graphs F locally common: is locally common. 12 +3 12 2 September 2012 +3 +3 2 +12 +3 4 Franek-Rödl + +12 4 + 6 55

Common graphs graph containing is locally common but not common. Not locally common: September 2012 56

Common graphs F common: is common. 8 - 1/2 +2 + +4 September 2012 Franek-Rödl =4 1/2 +2 +( -2 )2 57

Common graphs Hatami, Hladky, Kral, Norine, Razborov F common: Common graphs: Non-common graphs: Sidorenko graphs (bipartite? ) graph containing September 2012 Jagger, Stovícek, Thomason 58