Graph limits and graph homomorphisms Lszl Lovsz Microsoft










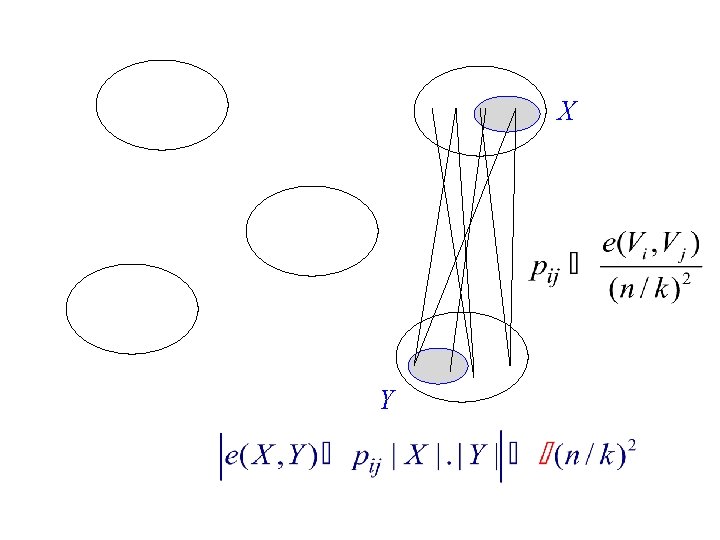



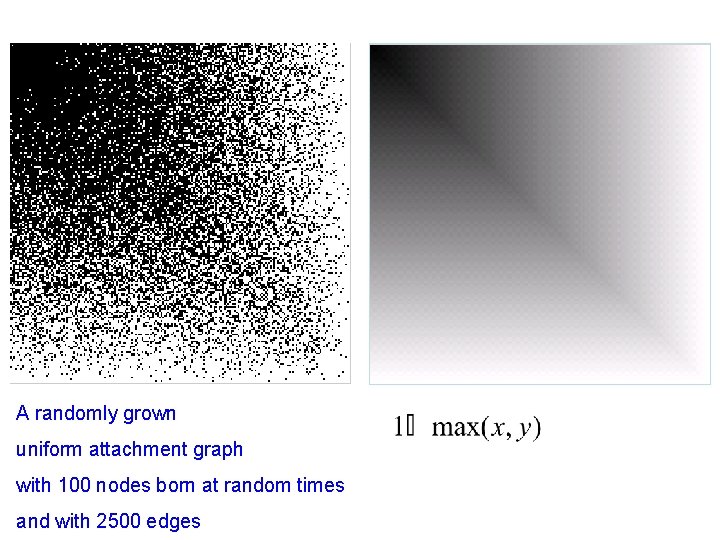












- Slides: 33

Graph limits and graph homomorphisms László Lovász Microsoft Research lovasz@microsoft. com

Why define limits of graph sequences? I. Very large graphs: -Internet -Social networks -Ecological systems -VLSI -Statistical physics -Brain Is there a good "small" approximation? Is there a good "continuous" approximation?

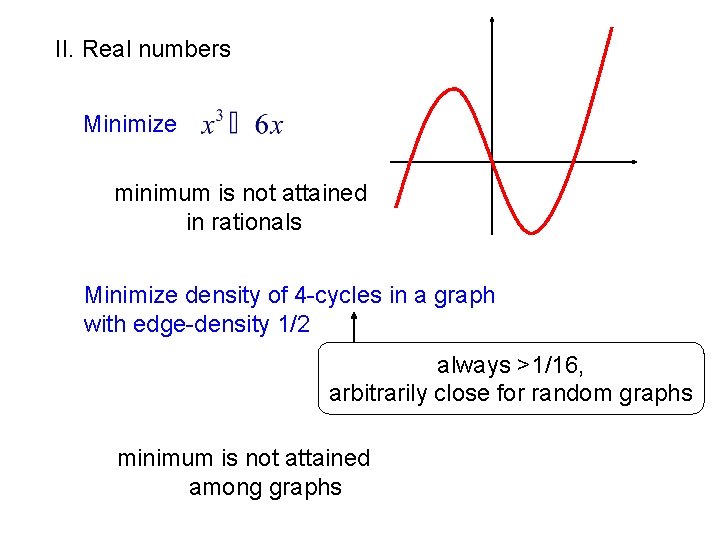
II. Real numbers Minimize minimum is not attained in rationals Minimize density of 4 -cycles in a graph with edge-density 1/2 always >1/16, arbitrarily close for random graphs minimum is not attained among graphs

Limits of sequences of graphs with bounded degree: Aldous, Benjamini-Schramm, Lyons, Elek Limits of sequences of dense graphs: Borgs, Chayes, L, Sós, B. Szegedy, Vesztergombi

Limits of graph sequences Which sequences are convergent? Is there a limit object? Which parameters are “continuous at infinity”?

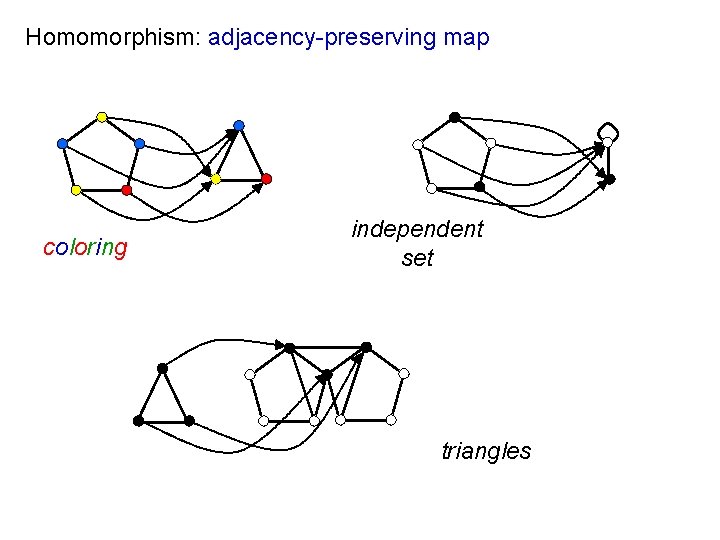
Homomorphism: adjacency-preserving map coloring independent set triangles

Probability that random map V(G) V(H) is a hom Weighted version:

Examples: hom(G, ) = # of independent sets in G

Which graph sequences are convergent? Example: random graphs with probability 1

Quasirandom graphs Thomason Chung – Graham – Wilson (Gn: n=1, 2, . . . ) is quasirandom: Example: Paley graphs p: prime 1 mod 4

Distance of graphs (Gn) is convergent Cauchy in the "Counting lemma": -metric.

Approximating by small graphs Szemerédi's Regularity Lemma 1974 Given >0 The nodes of graph can be partitioned into a small number of essentially equal parts so that difference at most 1 the bipartite graphs between 2 parts are essentially random (with different densities). with k 2 exceptions for subsets X, Y of parts Vi, Vj # of edges between X and Y is pij|X||Y| (n/k)2
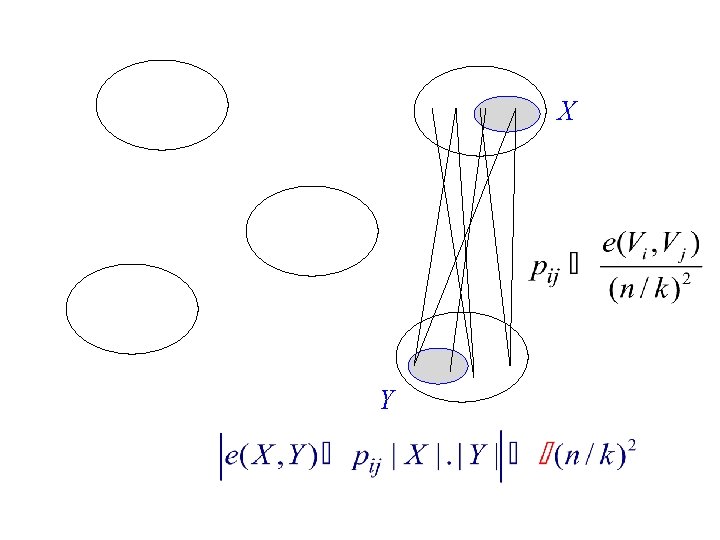
X Y

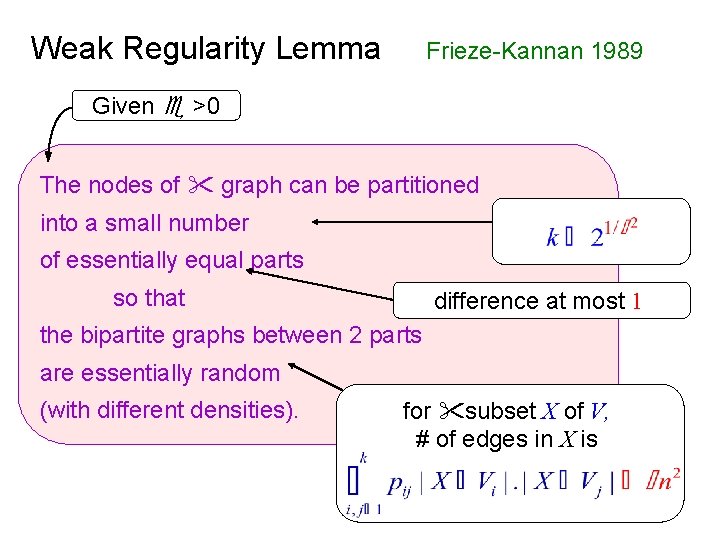
Weak Regularity Lemma Frieze-Kannan 1989 Given >0 The nodes of graph can be partitioned into a small number of essentially equal parts so that difference at most 1 the bipartite graphs between 2 parts are essentially random (with different densities). for subset X of V, # of edges in X is

Corollary of the "weak" Regularity Lemma:

Limits of graph sequences Which sequences are convergent? (G 1, G 2, . . . ) convergent Cauchy in the Is there a limit object? -metric.

A random graph with 100 nodes and with 2500 edges 1/2
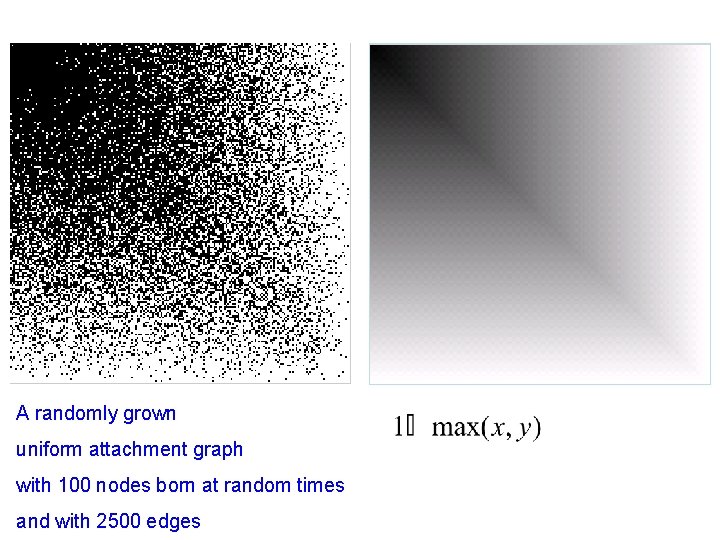
A randomly grown uniform attachment graph with 100 nodes born at random times and with 2500 edges

A randomly grown preferential attachment graph with 100 fixed nodes and with 5, 000 (multiple) edges

A randomly grown preferential attachment graph with 100 fixed nodes (ordered by degrees) and with 5, 000 edges

The limit object as a function

Example 1: Adjacency matrix of graph G: Associated function WG: 0 1 1 0 1 0 1 1 0 Example 2: t(F, W)= 2 -|E(F)| # of eulerian orientations of F

Distance of functions

Restatement of the "Weak" Regularity Lemma:

Summary of main results For every convergent graph sequence (Gn) there is a such that Szemerédi Lemma Conversely, W (Gn) such that W is essentially unique (up to measure-preserving transform).

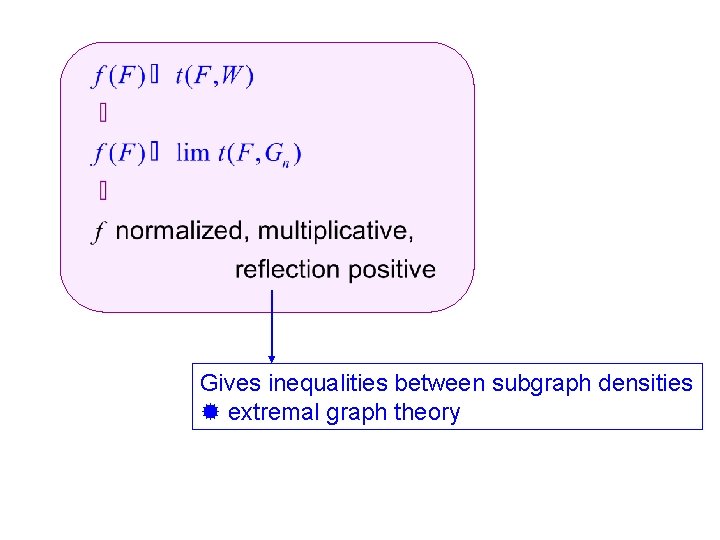
The limit object as a graph parameter is a graph parameter (normalized) (multiplicative) "connection matrices" are positive semidefinite (reflection positive)


Gives inequalities between subgraph densities extremal graph theory

The limit object as a random graph model W-random graphs:

The following are cryptomorphic: functions in W 0 modulo measure preserving transformations normalized, multiplicative and reflection positive graph parameters random graph models G(n) that are hereditary and independent on disjoint subsets ergodic invariant measures on

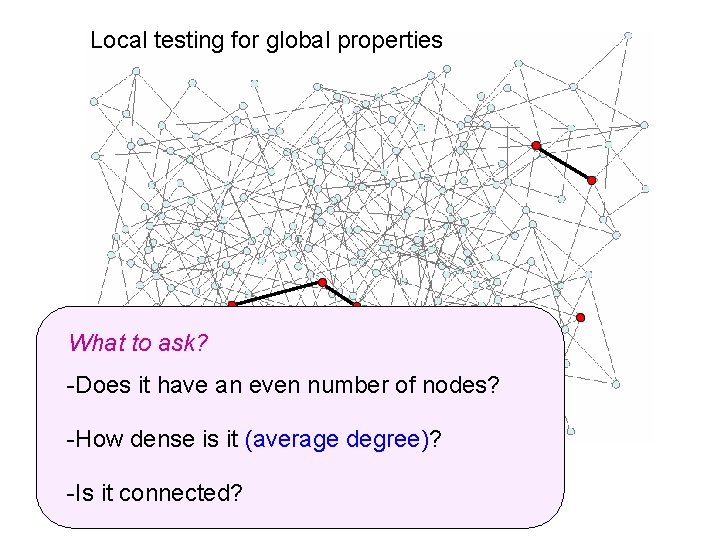
Local testing for global properties What to ask? -Does it have an even number of nodes? -How dense is it (average degree)? -Is it connected?

f is testable: Sk: random set of k nodes f is testable [(Gn) convergent f(Gn) convergent] The density of the largest cut can be estimated by local tests. Goldreich Goldwasser - Ron

max cut
 Graph limit theory
Graph limit theory Csereklei david
Csereklei david Lim as x approaches infinity
Lim as x approaches infinity Real limits statistics
Real limits statistics Lovasz graph limits
Lovasz graph limits Microsoft official academic course microsoft word 2016
Microsoft official academic course microsoft word 2016 Microsoft official academic course microsoft excel 2016
Microsoft official academic course microsoft excel 2016 Microsoft windows startwarren theverge
Microsoft windows startwarren theverge Microsoft excel merupakan progran aplikasi..
Microsoft excel merupakan progran aplikasi.. Microsoft official academic course microsoft word 2016
Microsoft official academic course microsoft word 2016 Limit and continuity solved problems
Limit and continuity solved problems Limits fits and tolerances lecture notes
Limits fits and tolerances lecture notes Radiation dose limits for workers and public pdf
Radiation dose limits for workers and public pdf Calculus chapter 2 limits and continuity answers
Calculus chapter 2 limits and continuity answers Fits and tolerance شرح
Fits and tolerance شرح Chapter 1 limits and their properties
Chapter 1 limits and their properties Limits and their properties
Limits and their properties Fundamental deviation
Fundamental deviation Ncert limits and derivatives pdf
Ncert limits and derivatives pdf Thomas calculus limits and continuity
Thomas calculus limits and continuity Consistency limits
Consistency limits Limits and derivatives
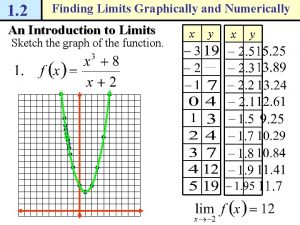
Limits and derivatives Understanding limits graphically and numerically
Understanding limits graphically and numerically Estimating limits numerically
Estimating limits numerically Find limit
Find limit Limits at infinity and horizontal asymptotes
Limits at infinity and horizontal asymptotes Finding limits graphically and numerically worksheet
Finding limits graphically and numerically worksheet Limit and continuity solved problems
Limit and continuity solved problems Finding limits graphically
Finding limits graphically Limits and continuity
Limits and continuity Limits graphically
Limits graphically Chapter 1 limits and their properties
Chapter 1 limits and their properties Limit of trigonometric functions examples
Limit of trigonometric functions examples Application of limits and continuity
Application of limits and continuity