ESTADO DE MATO GROSSO SECRETARIA DE CINCIA E













- Slides: 28

ESTADO DE MATO GROSSO SECRETARIA DE CIÊNCIA E TECNOLOGIA UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP DEPARTAMENTO DE ENGENHARIA CIVIL Geotecnia I Tensões no solo Ana Elza Dalla Roza anaelza 00@hotmail. com

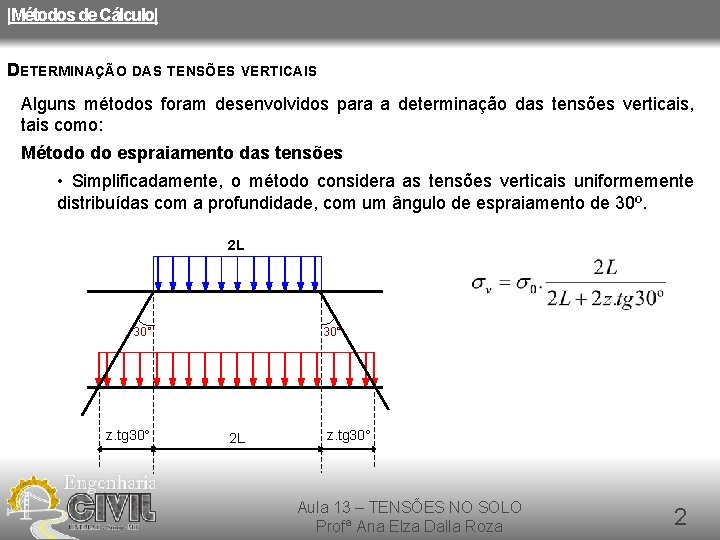
|Métodos de Cálculo| DETERMINAÇÃO DAS TENSÕES VERTICAIS Alguns métodos foram desenvolvidos para a determinação das tensões verticais, tais como: Método do espraiamento das tensões • Simplificadamente, o método considera as tensões verticais uniformemente distribuídas com a profundidade, com um ângulo de espraiamento de 30º. 2 L 30° z. tg 30° 2 L z. tg 30° Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza 2

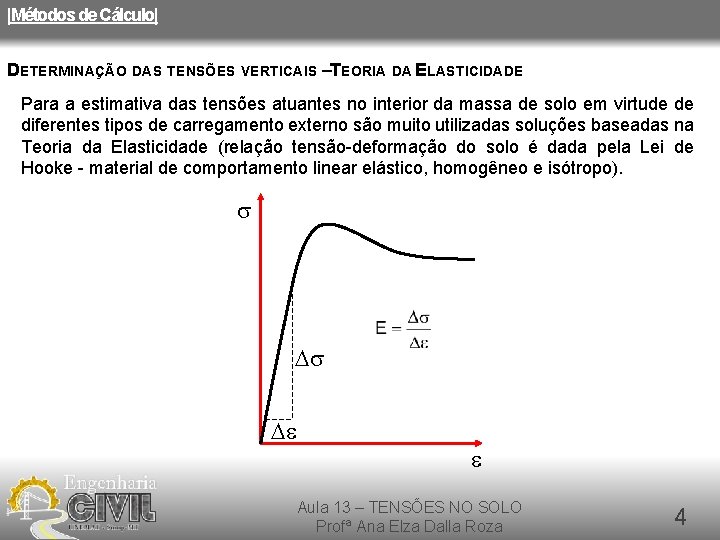
|Métodos de Cálculo| DETERMINAÇÃO DAS TENSÕES VERTICAIS –TEORIA DA ELASTICIDADE Para a estimativa das tensões atuantes no interior da massa de solo em virtude de diferentes tipos de carregamento externo são muito utilizadas soluções baseadas na Teoria da Elasticidade (relação tensão-deformação do solo é dada pela Lei de Hooke - material de comportamento linear elástico, homogêneo e isótropo). Um solo é dito isotrópico se os parâmetros definidos em um ponto são os mesmos em qualquer direção A isotropia reduz as constantes elásticas do solo em apenas duas: módulo de elasticidade (E) e coeficiente de Poisson (n) Se as constantes elásticas são as mesmas em todos os pontos de uma massa de solo então ele pode ser considerado homogêneo Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza 3

|Métodos de Cálculo| DETERMINAÇÃO DAS TENSÕES VERTICAIS –TEORIA DA ELASTICIDADE Para a estimativa das tensões atuantes no interior da massa de solo em virtude de diferentes tipos de carregamento externo são muito utilizadas soluções baseadas na Teoria da Elasticidade (relação tensão-deformação do solo é dada pela Lei de Hooke - material de comportamento linear elástico, homogêneo e isótropo). s Ds De e Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza 4

|Métodos de Cálculo| DETERMINAÇÃO DAS TENSÕES VERTICAIS –TEORIA DA ELASTICIDADE Entretanto, a aplicação de soluções mais simples da Teoria da Elasticidade aos solos é questionável, pois os mesmos podem não satisfazer as hipóteses: • Comportamento linear e elástico Para que seja válida, os acréscimos de tensão devem ser pequenos (pequenas deformações), tal que o estado de tensões seja muito distante da ruptura • Homogeneidade Foge da realidade na maioria dos casos. O solo é heterogêneo pela sua natureza e também apresenta relações tensão-deformação variáveis com a tensão de confinamento, logo variável com a profundidade • Isotropia O solo é, em muitos casos, anisotrópico pela natureza e arranjo de suas partículas. Entretanto, a condição de isotropia é válida para terrenos onde o solo mantém constituição uniforme por distâncias da ordem de algumas vezes a menor dimensão da área carregada Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza 5

|Métodos de Cálculo| DETERMINAÇÃO DAS TENSÕES VERTICAIS –TEORIA DA ELASTICIDADE Como ainda não há melhor alternativa para a análise do comportamento das obras e também porque tem tido uma avaliação satisfatória das tensões atuantes no solo, a Teoria da Elasticidade é aplicada como base de várias soluções desenvolvidas. Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza 6

|Métodos de Cálculo| DETERMINAÇÃO DAS TENSÕES VERTICAIS –TEORIA DA ELASTICIDADE Boussinesq - carga concentrada; Flamant - carga ao longo de uma linha de extensão infinita; Carothers-Terzaghi - carga uniformemente distribuída ao longo de uma faixa de extensão infinita; Osterberg - carga distribuída na forma de trapézio retangular em uma faixa de extensão infinita; Carothers - carga distribuída na forma de triângulo em uma faixa de extensão infinita; Love - carga uniforme sobre superfície circular; Soluções para carga uniforme sobre superfície retangular: • Newmark • Steinbrenner Solução para carga uniforme sobre superfície qualquer - Método das superposição de áreas (Ábaco circular de Newmark). Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza 7

|Métodos de Cálculo| SOLUÇÃO DE BOUSSENESQ – CARGA CONCENTRADA Nesta solução foram determinadas as tensões, deformações e deslocamentos no interior de uma massa elástica, homogênea e isotrópica, num semi-espaço infinito de superfície horizontal, devido a uma carga pontual aplicada na superfície deste semi-espaço. A equação de Boussinesq para o acréscimo de tensão vertical em qualquer ponto devido à aplicação de uma carga Q na superfície é: Q r z Sendo r e z definidos como: Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza sv 8

|Métodos de Cálculo| SOLUÇÃO DE BOUSSENESQ – CARGA CONCENTRADA Na vertical abaixo do ponto de aplicação da carga (r = 0), as tensões são iguais a: Q r z Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza sv 9

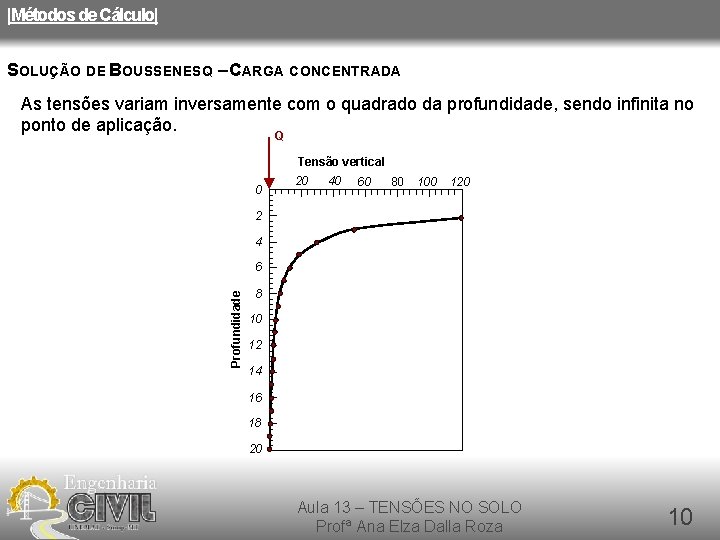
|Métodos de Cálculo| SOLUÇÃO DE BOUSSENESQ – CARGA CONCENTRADA As tensões variam inversamente com o quadrado da profundidade, sendo infinita no ponto de aplicação. Q Tensão vertical 0 20 40 60 80 100 120 2 4 Profundidade 6 8 10 12 14 16 18 20 Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza 10

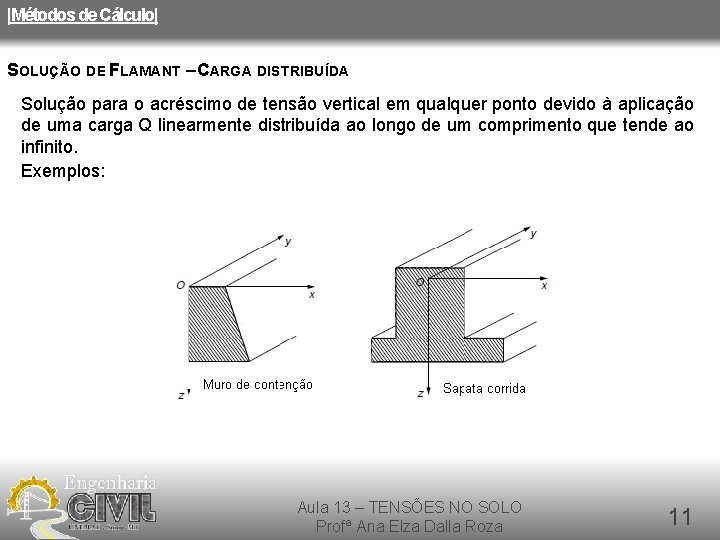
|Métodos de Cálculo| SOLUÇÃO DE FLAMANT – CARGA DISTRIBUÍDA Solução para o acréscimo de tensão vertical em qualquer ponto devido à aplicação de uma carga Q linearmente distribuída ao longo de um comprimento que tende ao infinito. Exemplos: Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza 11

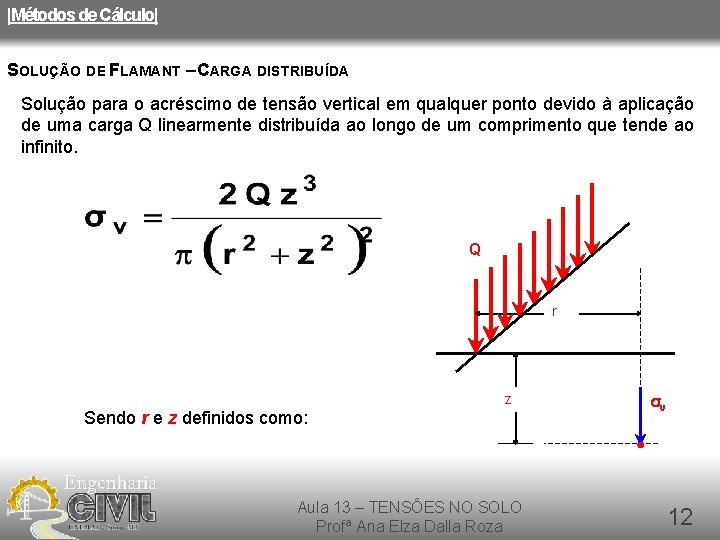
|Métodos de Cálculo| SOLUÇÃO DE FLAMANT – CARGA DISTRIBUÍDA Solução para o acréscimo de tensão vertical em qualquer ponto devido à aplicação de uma carga Q linearmente distribuída ao longo de um comprimento que tende ao infinito. Q r z Sendo r e z definidos como: Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza sv 12

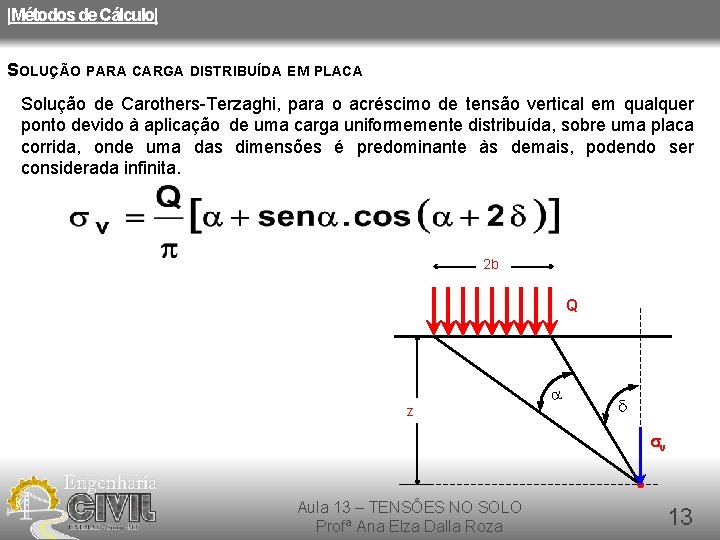
|Métodos de Cálculo| SOLUÇÃO PARA CARGA DISTRIBUÍDA EM PLACA Solução de Carothers-Terzaghi, para o acréscimo de tensão vertical em qualquer ponto devido à aplicação de uma carga uniformemente distribuída, sobre uma placa corrida, onde uma das dimensões é predominante às demais, podendo ser considerada infinita. 2 b Q z sv Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza 13

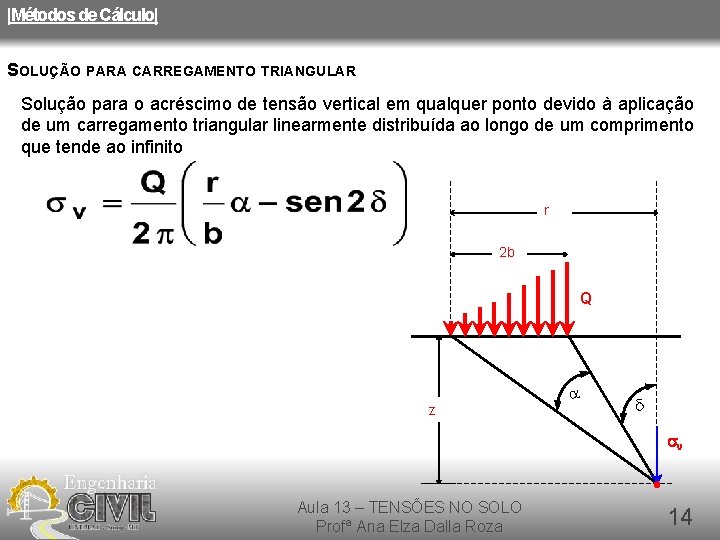
|Métodos de Cálculo| SOLUÇÃO PARA CARREGAMENTO TRIANGULAR Solução para o acréscimo de tensão vertical em qualquer ponto devido à aplicação de um carregamento triangular linearmente distribuída ao longo de um comprimento que tende ao infinito r 2 b Q z sv Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza 14

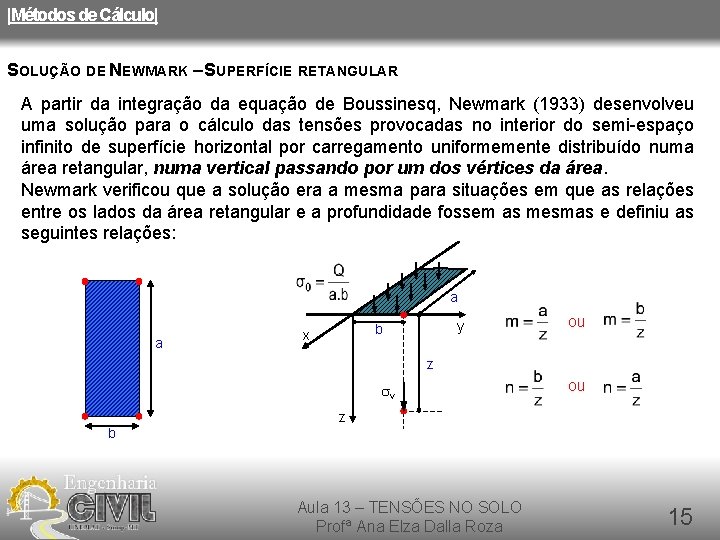
|Métodos de Cálculo| SOLUÇÃO DE NEWMARK – SUPERFÍCIE RETANGULAR A partir da integração da equação de Boussinesq, Newmark (1933) desenvolveu uma solução para o cálculo das tensões provocadas no interior do semi-espaço infinito de superfície horizontal por carregamento uniformemente distribuído numa área retangular, numa vertical passando por um dos vértices da área. Newmark verificou que a solução era a mesma para situações em que as relações entre os lados da área retangular e a profundidade fossem as mesmas e definiu as seguintes relações: a a y b x ou z sv ou z b Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza 15

|Métodos de Cálculo| SOLUÇÃO DE NEWMARK – SUPERFÍCIE RETANGULAR Em função destes parâmetros, a solução de Newmark é expressa pela equação: Trata-se uma solução muito trabalhosa, mas se considerarmos que a tensão num ponto qualquer é função só dos parâmetros m e n, a expressão pode ser reescrita como: sendo Is um coeficiente de influência que pode ser obtido a partir de um ábaco, em função de m e n. Com base no Princípio da Superposição dos Efeitos é possível determinar as tensões em qualquer outro ponto sob a placa ou fora dela. Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza 16

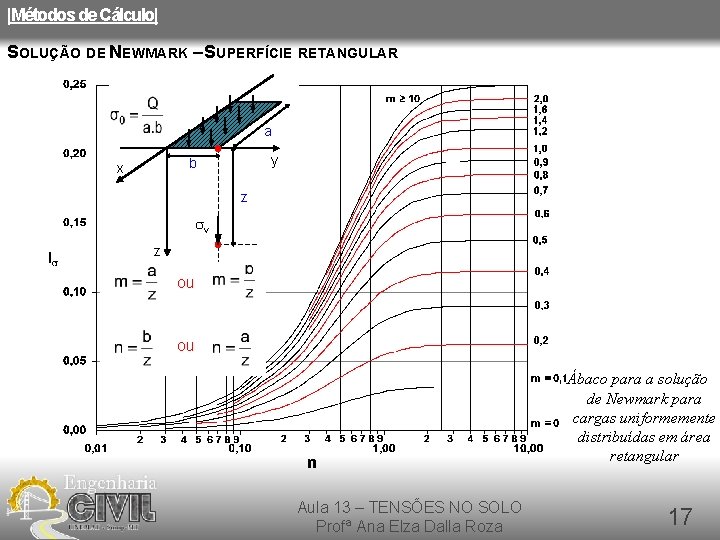
|Métodos de Cálculo| SOLUÇÃO DE NEWMARK – SUPERFÍCIE RETANGULAR a y b x z sv z ou ou Ábaco para a solução de Newmark para cargas uniformemente distribuídas em área retangular Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza 17

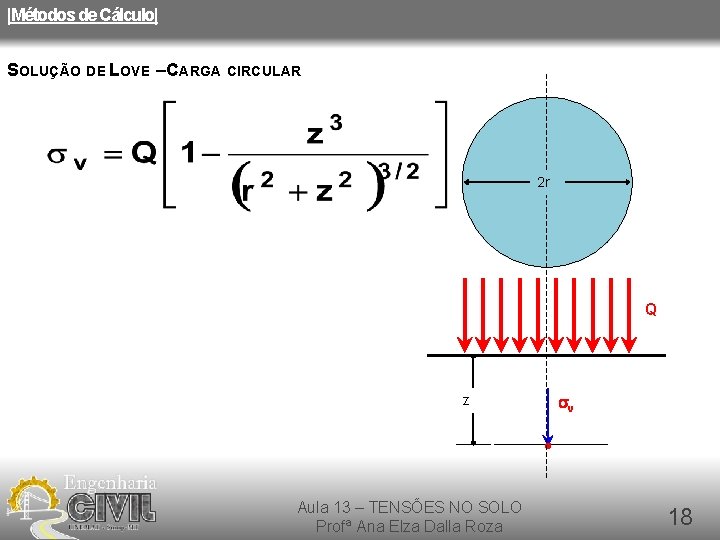
|Métodos de Cálculo| SOLUÇÃO DE LOVE – CARGA CIRCULAR 2 r Q z Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza sv 18

|Métodos de Cálculo| ÁBACO CIRCULAR DE NEWMARK Esta solução tem por base a equação de Love e o Princípio da Superposição dos Efeitos. Quando é aplicada uma carga uniformemente distribuída sobre uma superfície, a tensão gerada a uma dada profundidade é igual ao somatório dos efeitos dos carregamentos em áreas parciais. Para a construção do ábaco são traçados 10 círculos concêntricos cujo acréscimo de carga a um ponto do centro dos círculos situado a uma profundidade z corresponde a 10%, 20%, 30%, . . . da carga total aplicada. Logo, cada um dos anéis apresenta Iσ = 0, 1. Da equação de Love: Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza 19

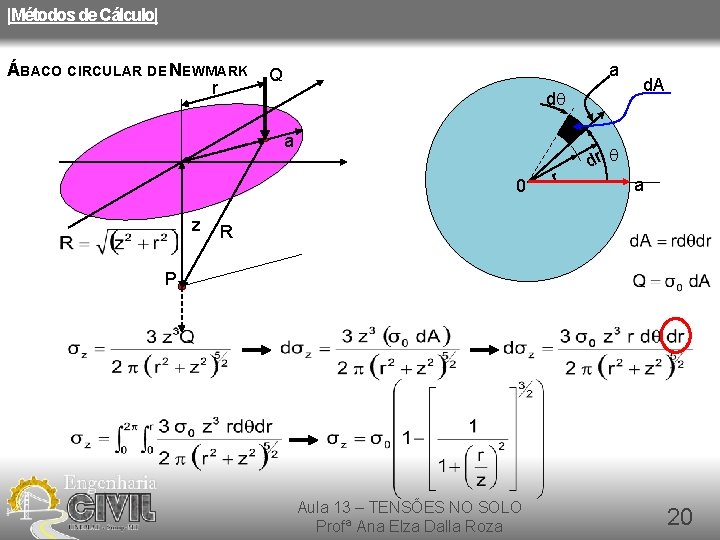
|Métodos de Cálculo| ÁBACO CIRCULAR DE NEWMARK r a Q dq a 0 z r d. A dr q a R P Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza 20

|Métodos de Cálculo| ÁBACO CIRCULAR DE NEWMARK Como Iσ = f(r/z), isolando r/z teremos: Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza 21

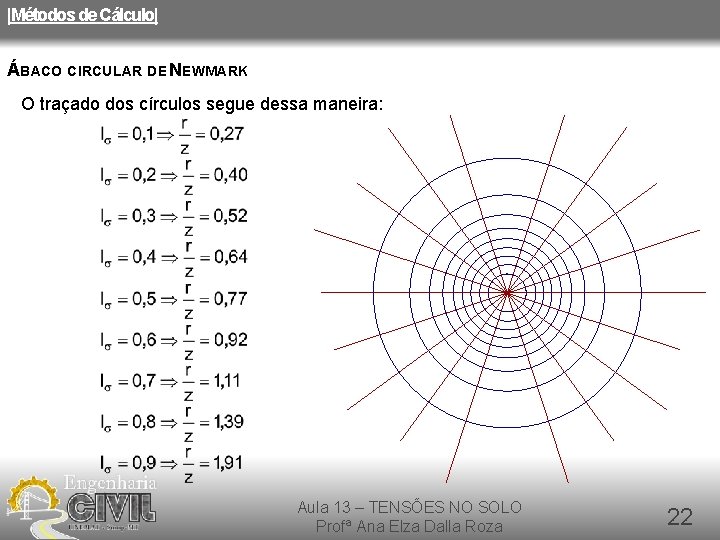
|Métodos de Cálculo| ÁBACO CIRCULAR DE NEWMARK O traçado dos círculos segue dessa maneira: Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza 22

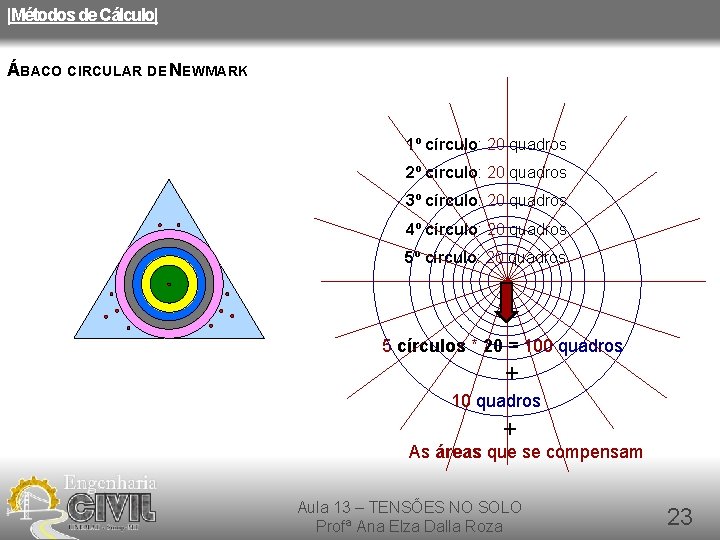
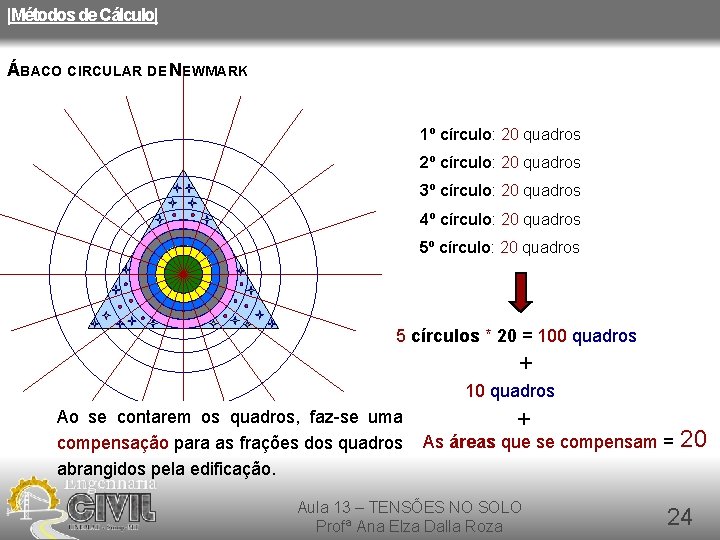
|Métodos de Cálculo| ÁBACO CIRCULAR DE NEWMARK 1º círculo: 20 quadros 2º círculo: 20 quadros 3º círculo: 20 quadros 4º círculo: 20 quadros 5º círculo: 20 quadros + 5 círculos * 20 = 100 quadros + 10 quadros + As áreas que se compensam Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza 23

|Métodos de Cálculo| ÁBACO CIRCULAR DE NEWMARK 1º círculo: 20 quadros 2º círculo: 20 quadros 3º círculo: 20 quadros 4º círculo: 20 quadros 5º círculo: 20 quadros + 5 círculos * 20 = 100 quadros + 10 quadros Ao se contarem os quadros, faz-se uma compensação para as frações dos quadros abrangidos pela edificação. + As áreas que se compensam = Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza 20 24

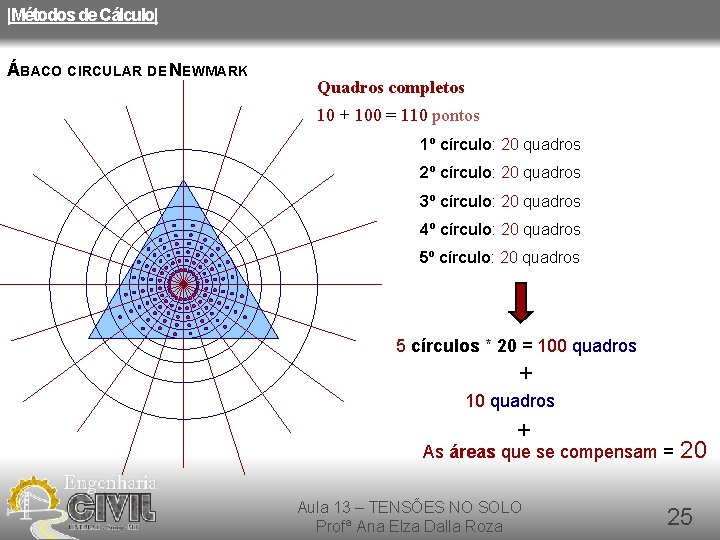
|Métodos de Cálculo| ÁBACO CIRCULAR DE NEWMARK Quadros completos 10 + 100 = 110 pontos 1º círculo: 20 quadros 2º círculo: 20 quadros 3º círculo: 20 quadros 4º círculo: 20 quadros 5º círculo: 20 quadros + 5 círculos * 20 = 100 quadros + 10 quadros + As áreas que se compensam = Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza 20 25

|Métodos de Cálculo| ÁBACO CIRCULAR DE NEWMARK O ábaco é dividido em 20 setores de igual área, originando trapézios circulares (“quadros”) cuja unidade de influência Iσ = 0, 005. Contam-se quantos quadros foram ocupados pela planta. Cada quadro carregado provoca no ponto 0, 5% da tensão aplicada. O nº de quadros vezes o valor da influência (0, 005) vezes a tensão aplicada indica a tensão provocada por todo o carregamento da superfície. Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza 26

|Métodos de Cálculo| SOLUÇÃO DE WETERGAARD Para o caso de solos estratificados, material fino entremeado por lentes de areia, caso de solos sedimentares, a solução de Boussinesq não se aplica. Nesses solos, as camadas com diferentes materiais dão ao solo uma certa resistência as deformações horizontais Nesse caso, utiliza-se a solução de Westergaard que considera deformações laterais nulas. Aula 13 – TENSÕES NO SOLO Profª Ana Elza Dalla Roza 27

ESTADO DE MATO GROSSO SECRETARIA DE CIÊNCIA E TECNOLOGIA UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP DEPARTAMENTO DE ENGENHARIA CIVIL Mecânica dos Solos I Tensões no solo Ana Elza Dalla Roza anaelza 00@hotmail. com
 Escarpment definition geography
Escarpment definition geography Bandeira do mato grosso do sul
Bandeira do mato grosso do sul Massacre da baía do garcez
Massacre da baía do garcez Acincia
Acincia Significado de genocida
Significado de genocida Secretaria do estado de santa catarina
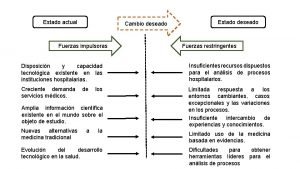
Secretaria do estado de santa catarina Fuerzas impulsoras
Fuerzas impulsoras Uccello piu veloce del mondo
Uccello piu veloce del mondo Graciela grosso
Graciela grosso A grosso has a group of soloists rather
A grosso has a group of soloists rather Válvula ileocecal
Válvula ileocecal órgãos do sistema digestório
órgãos do sistema digestório Cabo coaxial fino e grosso
Cabo coaxial fino e grosso Concerto grosso definicion
Concerto grosso definicion Graciela grosso
Graciela grosso Miopatia por corticoides
Miopatia por corticoides Definition concerto grosso
Definition concerto grosso Draga vlak u snijegu
Draga vlak u snijegu Instituto federal
Instituto federal Ay que disparate
Ay que disparate Tomat mato kasvatamine
Tomat mato kasvatamine Vlak u snijegu kondukter
Vlak u snijegu kondukter Ulazne jedinice
Ulazne jedinice El angel de jehova mato a los asirios
El angel de jehova mato a los asirios Tomati varrepõletik
Tomati varrepõletik Film družba pere kvržice mato lovrak
Film družba pere kvržice mato lovrak Absoliutinis luzio rodiklis
Absoliutinis luzio rodiklis Majeutika sokrat
Majeutika sokrat Mato
Mato