Econometrics Econ 405 Chapter 6 MULTIPLE REGRESSION ANALYSIS

Econometrics Econ. 405 Chapter 6: MULTIPLE REGRESSION ANALYSIS

I. Regression Analysis Beyond Simple Models § In reality, economic theory is applied using more than one explanatory variable. § Thus, the simple regression model (discussed last chapter) needs to be extended to include more than two variables. § Adding more variables into the regression model requires revisiting the Classical Linear Regression Model (CLRM) assumptions.

§ Multiple regression analysis is more appropriate to “ceteris paribus” analysis as it allows for controlling several variables that simultaneously influence the dependent variable. § In this case, the general functional form represents the relationship between the DV and the IVs which would build better model for estimating the dependent variable.

II. Motivation for Multiple Regression § Incorporate more explanatory factors into the model. § Explicitly hold fixed other factors that otherwise would be in the error tern (u). § Allow for more flexible functional forms § So, the multiple regression would solve problems that cannot be solved by simple regression.

§ In Model (1): All factors that could have affected Wage are thrown into the error term (u). Thus (u) would be correlated to “Education” so we should assume that (u) &(X) are uncorrelated (CLRM Assumption # 6). § In Model (2): Measuring with confidence the effect of education on wage holding experience fixed

III. Features of Multiple Regression •

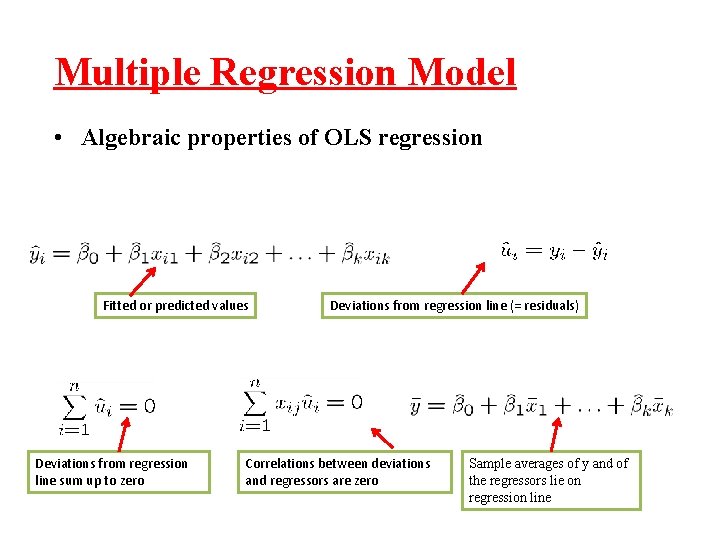
Properties of OLS Regression Recall: Simple Regression Model • Algebraic properties of OLS regression Fitted or predicted values Deviations from regression line sum up to zero Deviations from regression line (= residuals) Correlation between deviations and regressors is zero Sample averages of y and x lie on regression line

Multiple Regression Model • Algebraic properties of OLS regression Fitted or predicted values Deviations from regression line sum up to zero Deviations from regression line (= residuals) Correlations between deviations and regressors are zero Sample averages of y and of the regressors lie on regression line

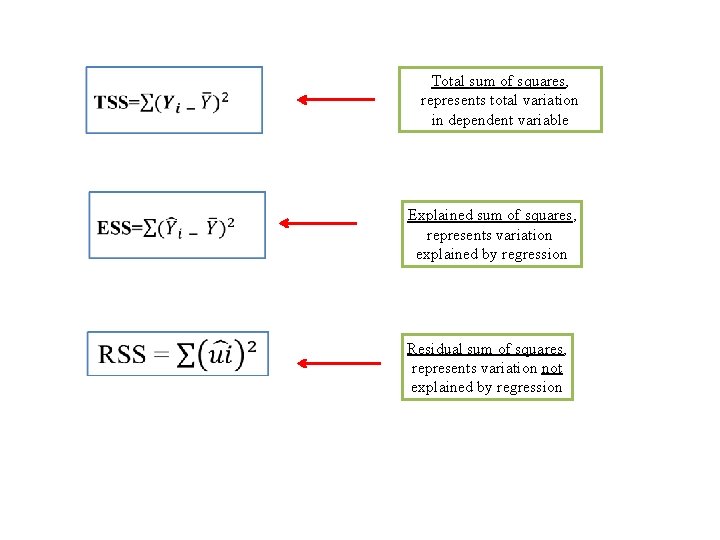
IV. Goodness of Fit (R²) Accordingly: q the Goodness-of-Fit is measures of variation to to show “How well does the explanatory variable explain the dependent variable? “ § TSS= total sum of squares § ESS= explained sum of squares § RSS= residual sum of squares

Total sum of squares, represents total variation in dependent variable Explained sum of squares, represents variation explained by regression Residual sum of squares, represents variation not explained by regression

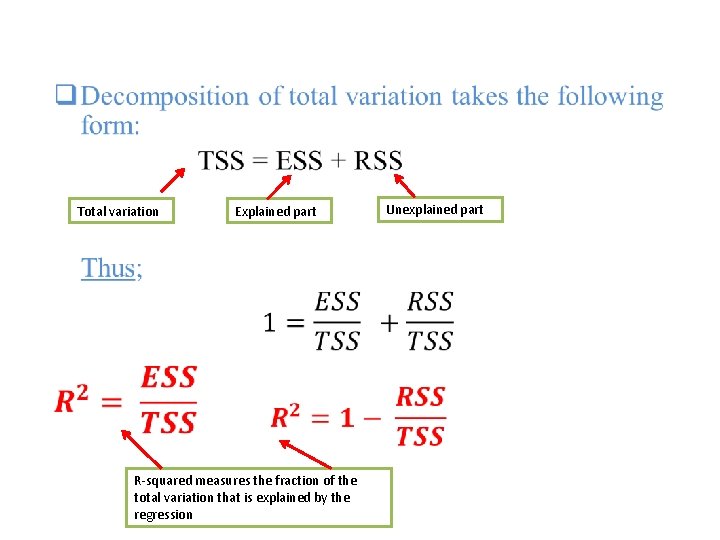
• Total variation Explained part R-squared measures the fraction of the total variation that is explained by the regression Unexplained part

• The Goodness-of-Fit is measures of variation to show “How well does the explanatory variable explain the dependent variable“, thus under the multiple regression model, it looks like the following:

V. Assumptions of the Multiple Regression Model § We continue within the framework of the classical linear regression model (CLRM) and to use the method of ordinary least squares (OLS) to estimate the coefficients. § The simplest possible multiple regression model is the three-variable regression, with one DV and two IVs. § Accordingly, CLRM consists of the following assumption;

Assumptions: 1 - linearity : Yi = β 0 + β 1 X 1 i + β 2 X 2 i + ui 2 - X values are fixed in repated sample; E(Yi /X 1 i , X 2 i ) = β 0 + β 1 X 1 i + β 2 X 2 i + ui 3 - Zero mean value of “ui”: E(ui | X 1 i , X 2 i) = 0 for each i 4 -No serial correlation (autocorrelation): cov (ui , uj ) = 0 i ≠ j

5 -Homoscedasticity: var (ui) = σ2 6 -Zero covariance between ui and each X variable: cov (ui , X 1 i) = cov (ui , X 2 i) = 0 7 - Number of observation vs number of parameters: N > # of parameters

8 - Varilability in Xs values: No specification bias 9 -The regression model is correctly specified: No specification bias 10 - No exact collinearity (perfect multicollinearity) between the X variables:

Now: § Which CLRM assumptions are appropriate for simple regression model and which are appropriate for multiple regression model? § What is the key CLRM assumption for multiple regression model?

Revisit the 10 th Assumption: § There be no exact linear relationship between X 1 and X 2, i. e. , no collinearity or no multicollinearity. § Informally, no collinearity means none of the regressors can be written as exact linear combinations of the remaining regressors in the model. Formally, no collinearity means that there exists no set of numbers, λ 1 and λ 2, not both zero such that; λ 1 X 1 i + λ 2 X 2 i = 0

§ If such an exact linear relationship exists, then X 1 and X 2 are said to be collinear or linearly dependent. On the other hand, if last equation holds true only when λ 2 = λ 3 = 0, then X 1 and X 2 are said to be linearly independent; X 1 i = − 4 X 2 i or X 1 i + 4 X 2 i = 0 § If the two variables are linearly dependent, and if both are included in a regression model, we will have perfect collinearity or an exact linear relationship between the two regressors.

• The Importance of Assumptions:

Discussion of Assumption (3): E(ui | X 1 i , X 2 i) = 0 § Explanatory variables that are correlated with the error term are called endogenous; endogeneity is a violation of this assumption. § Explanatory variables that are uncorrelated with the error term are called exogenous; this assumption holds if all explanatory variables are exogenous. § Exogeneity is the key assumption for a causal interpretation of the regression, and for unbiasedness of the OLS estimators.

The Importance of Assumptions: Assumption (6): Homoscedasticity; var (ui) = σ2 § The value of the explanatory variables must contain no information about the variance of the unobserved factors.

VI. Multiple Regression Analysis: Estimation 1 - Estimating the error variance: § An unbiased estimate of the error variance can be obtained by subtracting the number of estimated regression coefficients (k) from the number of observations (n). § (n-k)is also called the degrees of freedom. The (n) estimated squared residuals in the sum are not completely independent but related through the k+1 equations that define the first order conditions of the minimization problem.

2 - Sampling variances of OLS slope estimators: Variance of the error term TSSj R-squared from a regression of explanatory variable xj on all other independent variables (including a constant)

3 - Standard Errors for Regression Coefficients: § The estimated standard deviations of the regression coefficients are called “standard errors“. They measure how precisely the regression coefficients are estimated. TSSj The estimated sampling variation of the Estimated B § Note that these formulas are only valid under CLRM assumptions(in particular, there has to be homoscedasticity)

The Components of OLS Variances: 1) The error variance – A high error variance increases the sampling variance because there is more “ noise“ in the equation. – A large error variance necessarily makes estimates imprecise. 2) The total sample variation in the explanatory variable – More sample variation leads to more precise estimates. – Total sample variation automatically increases with the sample size. – Increasing the sample size is thus a way to get more precise estimates.

3) Linear relationships among the independent variables - Regress xj on all other independent variables (including a constant). - The higher R² of this regression, the more likely xj can be linearly explained by the other independent variables. - In such case, sampling variance of ( ) will be the higher, the more likely explanatory variable xj can be linearly explained by other independent variables. - The problem of almost linearly dependent explanatory variables is called multicollinearity (next be explained).

Example: Multicollinearity Average standardized test score of school Expenditures for teachers Expenditures for instructional materials Other expenditures § The different expenditure categories will be strongly correlated because if a school has a lot of resources it will spend a lot on everything. § It will be hard to estimate the differential effects of different expenditure categories because all expenditures are either high or low. For precise estimates of the differential effects, one would need information about situations where expenditure categories change differentially. § Therefore, sampling variance of the estimated effects will be large.

Further Discussion of Multicollinearity - According to the example, it would probably be better to lump all expenditure categories together because effects cannot be disentangled. - In other cases, dropping some independent variables may reduce multicollinearity (but this may lead to omitted variable bias- Discussed Next) - Only the sampling variance of the variables involved in multicollinearity will be inflated; the estimates of other effects may be very precise. - Multicollinearity may be detected through a test called “Variance Inflation Factors (VIF)“ (Explained next chapters)

The issue of Including and Omitting variables Case (1): Including irrelevant variables in a regression model: B 3= 0 in the population § No problem , still estimated coefficients are unbiased because § However, including irrevelant variables may increase sampling variance. That would make the OLS estimates will not be “best” ( BLUE), Why? ? .

Case (2): Omitting relevant variables in a regression model True model (contains x 1 and x 2) Estimated model (x 2 is omitted) Example: If y is only regressed on x 1 this will be the estimated intercept If x 1 and x 2 are correlated, it means a linear regression relationship between them If y is only regressed on x 1, this will be the estimated slope on x 1 error term • Conclusion: All estimated coefficients will be biased

• Will both be positive § The return to education will be overestimated because § It will look as if people with many years of education earn very high wages, but this is partly due to the fact that people with more education are also more able on average.

Variances in Misspecified Models § The choice of whether to include a particular variable in a regression can be made by analyzing the tradeoff between bias and variance. True population model Estimated model (1) Estimated model (2) – It might be the case that the likely omitted variable bias in the misspecified model (2) is overcompensated by a smaller variance.

TSS 1 Recall, Conditional on x 1 and x 2 , the variance in model (2) is always smaller than that in model (1) Case (1): Estimater of both Models are Unbiased Conclusion: Do not include irrelevant regressors Case (2): Estimater of X 1 in Model (2) is Biased Trade off bias and variance; Caution: bias will not vanish even in large samples

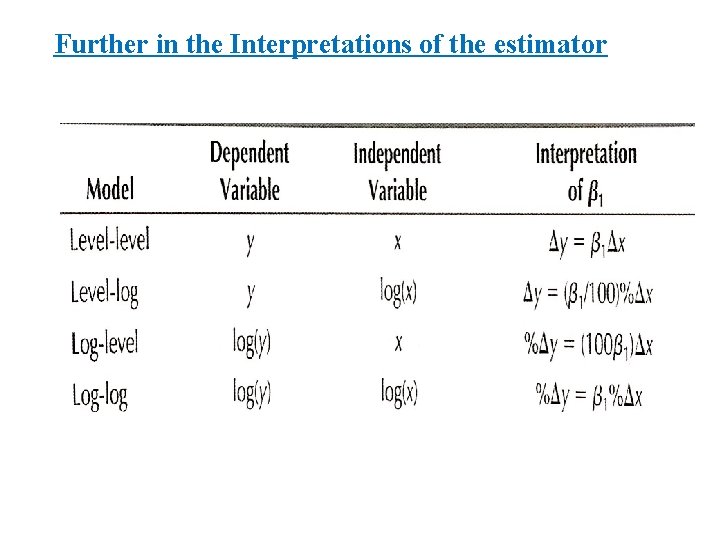
Further in the Interpretations of the estimator