ECE 465 Digital Systems Lecture Notes 8 Sequential

ECE 465: Digital Systems Lecture Notes # 8 Sequential Circuit (Finite-State Machine) Design SHANTANU DUTT Department of Electrical and Computer Engineering University of Illinois, Chicago Phone: (312) 355 -1314: e-mail: dutt@eecs. uic. edu URL: http: //www. eecs. uic. edu/~dutt 1

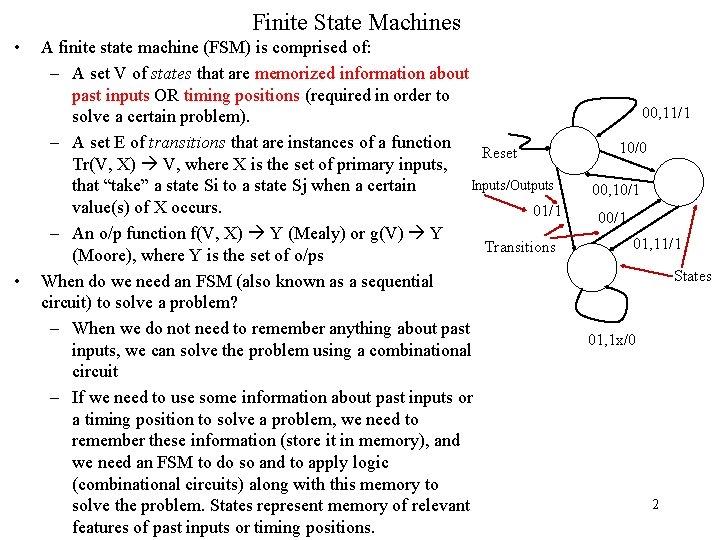
Finite State Machines • • A finite state machine (FSM) is comprised of: – A set V of states that are memorized information about past inputs OR timing positions (required in order to solve a certain problem). – A set E of transitions that are instances of a function Reset Tr(V, X) V, where X is the set of primary inputs, Inputs/Outputs that “take” a state Si to a state Sj when a certain value(s) of X occurs. 01/1 – An o/p function f(V, X) Y (Mealy) or g(V) Y Transitions (Moore), where Y is the set of o/ps When do we need an FSM (also known as a sequential circuit) to solve a problem? – When we do not need to remember anything about past inputs, we can solve the problem using a combinational circuit – If we need to use some information about past inputs or a timing position to solve a problem, we need to remember these information (store it in memory), and we need an FSM to do so and to apply logic (combinational circuits) along with this memory to solve the problem. States represent memory of relevant features of past inputs or timing positions. 00, 11/1 10/0 00, 10/1 01, 11/1 States 01, 1 x/0 2

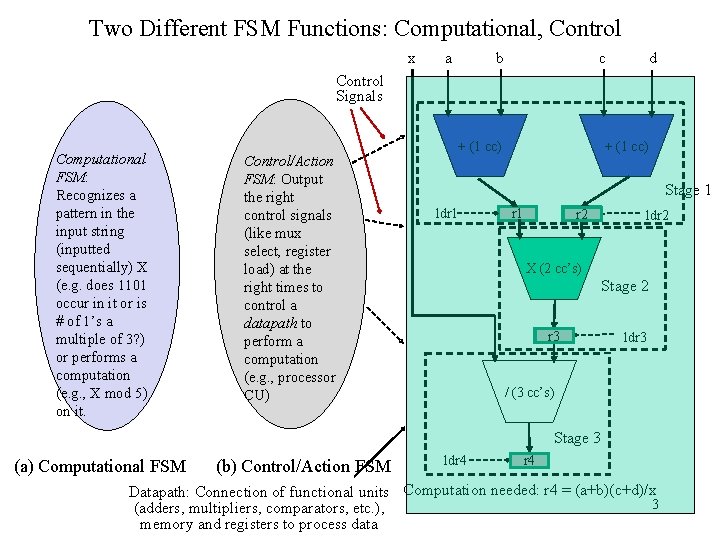
Two Different FSM Functions: Computational, Control x a b c d Control Signals Computational FSM: Recognizes a pattern in the input string (inputted sequentially) X (e. g. does 1101 occur in it or is # of 1’s a multiple of 3? ) or performs a computation (e. g. , X mod 5) on it. Control/Action FSM: Output the right control signals (like mux select, register load) at the right times to control a datapath to perform a computation (e. g. , processor CU) + (1 cc) Stage 1 ldr 1 r 2 ldr 2 X (2 cc’s) Stage 2 r 3 ldr 3 / (3 cc’s) Stage 3 (a) Computational FSM (b) Control/Action FSM ldr 4 Datapath: Connection of functional units Computation needed: r 4 = (a+b)(c+d)/x 3 (adders, multipliers, comparators, etc. ), memory and registers to process data

Finite State Machine (FSM) Design • Example : Problem Statement There is a bit-serial I/P line. Design an FSM that outputs a ‘ 0’ if an even # of 1’s have been received on the I/P line and the outputs a ‘ 1’ otherwise. • When do we need an FSM (i. e. , seq ckt) to solve a problem rather than a combinational ckt? • Ans: When the problem requires the design to remember something about past inputs in order to solve the problem. • Note: FSMs are different from counters in the sense that they have external I/Ps, and state transitions are dependent on these I/Ps and the current state. x FSM O/p y CLK 4

Digression 1: Setup Times and Hold Time of FFs • Assume, positive edge-triggered D-FF D THold relates to sensitivity period of FF (when it responds to inputs just after the +ve edge of the clock appears). CLK TSetup relates to propagation delays of The high point of various gates in the FF. the CLK determines the positive edge’s arrival. • Need the D-input to be stable at least TSetup time before the +ve edge of the clock appears • Need the D-input to remain stable at least THold time after the +ve edge of the clock appears 5

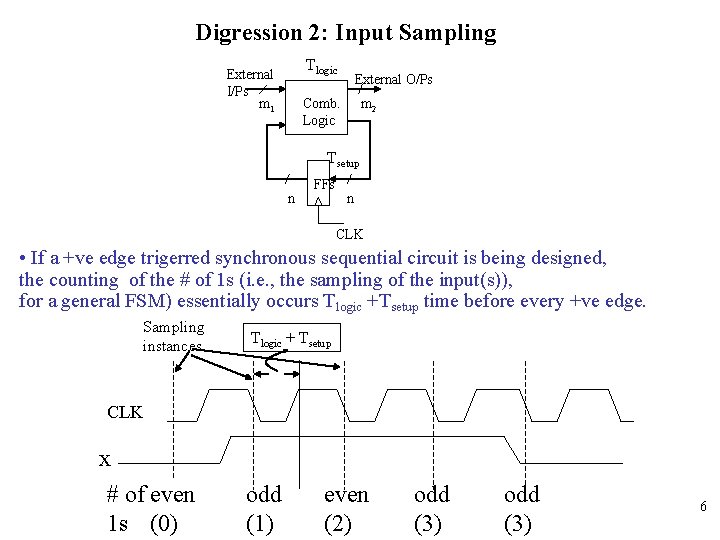
Digression 2: Input Sampling Tlogic External I/Ps m 1 External O/Ps Comb. Logic m 2 Tsetup n FFs n CLK • If a +ve edge trigerred synchronous sequential circuit is being designed, the counting of the # of 1 s (i. e. , the sampling of the input(s)), for a general FSM) essentially occurs Tlogic +Tsetup time before every +ve edge. Sampling instances Tlogic + Tsetup CLK x # of even 1 s (0) odd (1) even (2) odd (3) 6

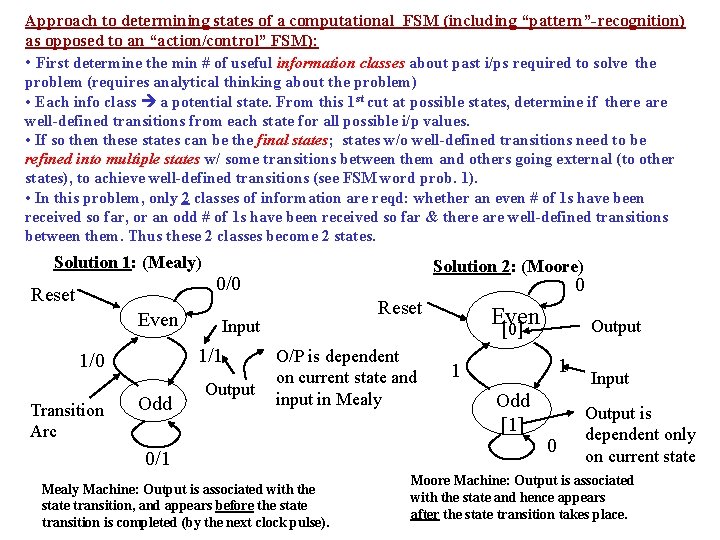
Approach to determining states of a computational FSM (including “pattern”-recognition) as opposed to an “action/control” FSM): • First determine the min # of useful information classes about past i/ps required to solve the problem (requires analytical thinking about the problem) • Each info class a potential state. From this 1 st cut at possible states, determine if there are well-defined transitions from each state for all possible i/p values. • If so then these states can be the final states; states w/o well-defined transitions need to be refined into multiple states w/ some transitions between them and others going external (to other states), to achieve well-defined transitions (see FSM word prob. 1). • In this problem, only 2 classes of information are reqd: whether an even # of 1 s have been received so far, or an odd # of 1 s have been received so far & there are well-defined transitions between them. Thus these 2 classes become 2 states. Solution 1: (Mealy) Reset Even Transition Arc 0/0 Odd 0 Reset Input 1/1 1/0 Solution 2: (Moore) Output O/P is dependent on current state and input in Mealy 0/1 Mealy Machine: Output is associated with the state transition, and appears before the state transition is completed (by the next clock pulse). Even [0] Output 1 1 Odd [1] 0 Input Output is dependent only on current state Moore Machine: Output is associated with the state and hence appears after the state transition takes place.

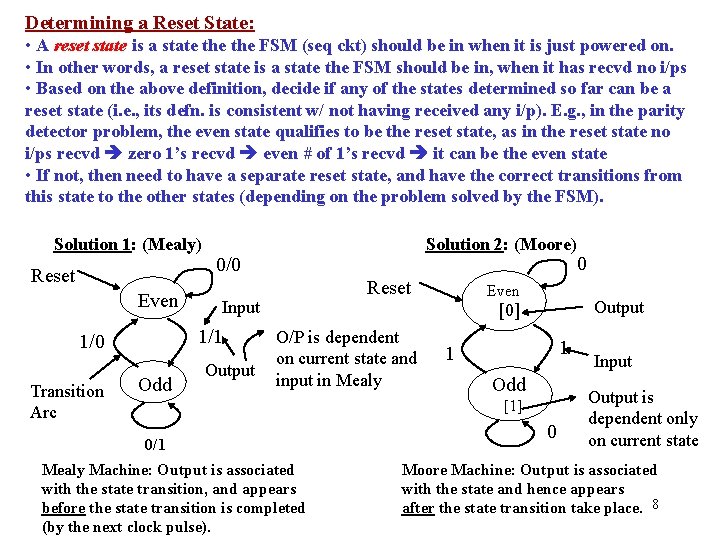
Determining a Reset State: • A reset state is a state the FSM (seq ckt) should be in when it is just powered on. • In other words, a reset state is a state the FSM should be in, when it has recvd no i/ps • Based on the above definition, decide if any of the states determined so far can be a reset state (i. e. , its defn. is consistent w/ not having received any i/p). E. g. , in the parity detector problem, the even state qualifies to be the reset state, as in the reset state no i/ps recvd zero 1’s recvd even # of 1’s recvd it can be the even state • If not, then need to have a separate reset state, and have the correct transitions from this state to the other states (depending on the problem solved by the FSM). Solution 1: (Mealy) Reset Even Transition Arc 0/0 Odd Reset Input 1/1 1/0 Solution 2: (Moore) Output Even Output [0] O/P is dependent on current state and input in Mealy 1 1 Odd [1] 0/1 Mealy Machine: Output is associated with the state transition, and appears before the state transition is completed (by the next clock pulse). 0 0 Input Output is dependent only on current state Moore Machine: Output is associated with the state and hence appears after the state transition take place. 8

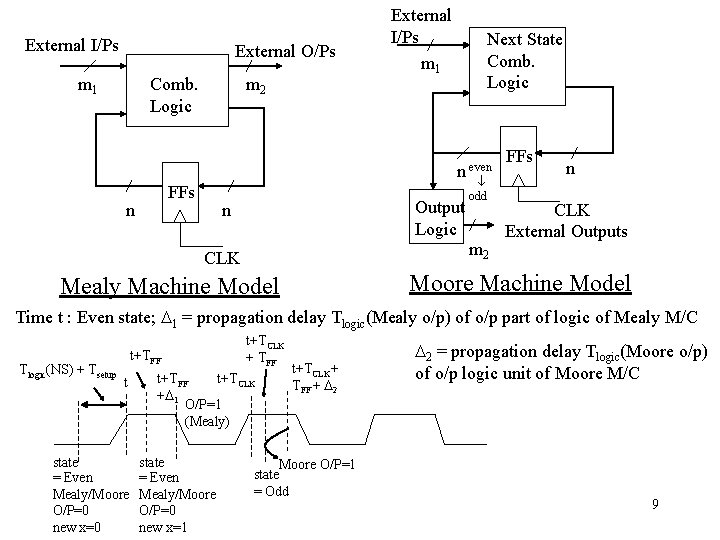
External I/Ps External O/Ps m 1 Comb. Logic m 2 FFs n External I/Ps m 1 Next State Comb. Logic n even odd Output Logic n m 2 CLK FFs n CLK External Outputs Moore Machine Model Mealy Machine Model Time t : Even state; 1 = propagation delay Tlogic(Mealy o/p) of o/p part of logic of Mealy M/C Tlogic(NS) + Tsetup t+TFF t state = Even Mealy/Moore O/P=0 new x=0 t+TCLK + TFF t+TCLK + 1 O/P=1 (Mealy) state = Even Mealy/Moore O/P=0 new x=1 t+TCLK+ TFF + 2 Moore O/P=1 state = Odd 2 = propagation delay Tlogic(Moore o/p) of o/p logic unit of Moore M/C 9

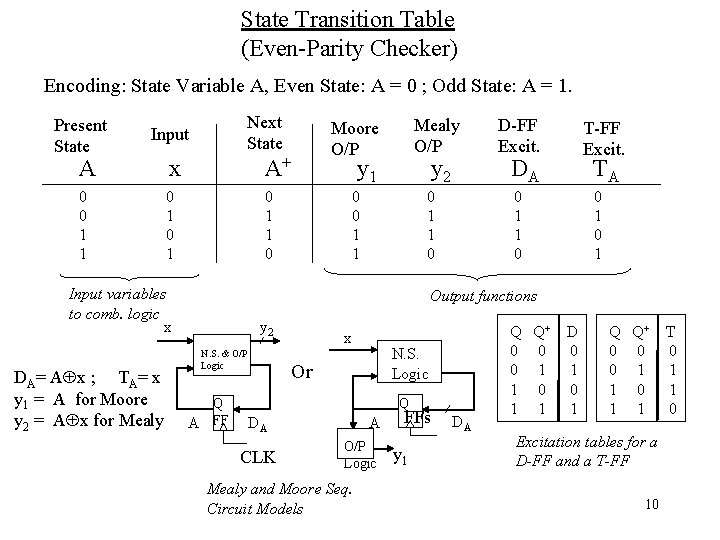
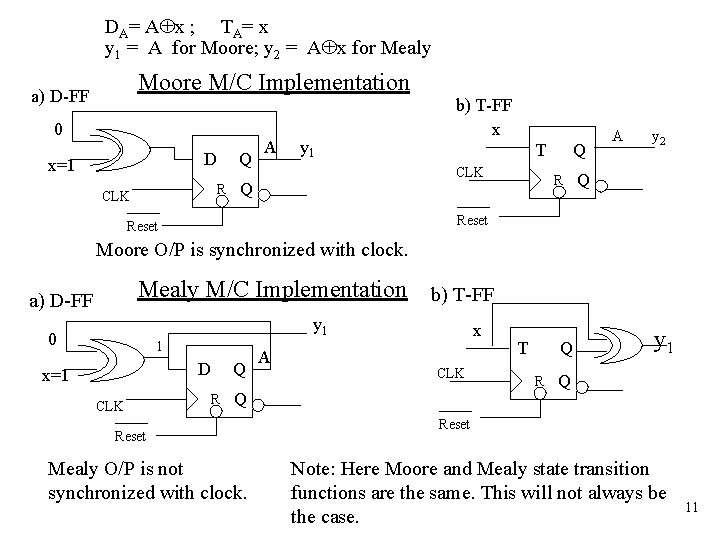
State Transition Table (Even-Parity Checker) Encoding: State Variable A, Even State: A = 0 ; Odd State: A = 1. Next State Present State Input A x A+ 0 0 1 1 0 1 0 1 1 0 Input variables to comb. logic y 1 y 2 0 0 1 1 0 D-FF Excit. T-FF Excit. DA TA 0 1 1 0 0 1 Output functions y 2 x DA= A x ; TA= x y 1 = A for Moore y 2 = A x for Mealy O/P Moore O/P N. S. & O/P Logic Q A FF x N. S. Logic Or Q DA CLK A O/P Logic Mealy and Moore Seq. Circuit Models FFs y 1 DA Q Q+ 0 0 0 1 1 D 0 1 Q Q+ 0 0 0 1 1 Excitation tables for a D-FF and a T-FF 10 T 0 1 1 0

DA= A x ; TA= x y 1 = A for Moore; y 2 = A x for Mealy Moore M/C Implementation a) D-FF 0 D x=1 Q R CLK A y 1 b) T-FF x T CLK Q Q R A y 2 Q Reset Moore O/P is synchronized with clock. Mealy M/C Implementation a) D-FF b) T-FF y 1 0 1 D x=1 CLK Q R A x CLK Q Reset Mealy O/P is not synchronized with clock. T Q R y 1 Q Reset Note: Here Moore and Mealy state transition functions are the same. This will not always be the case. 11

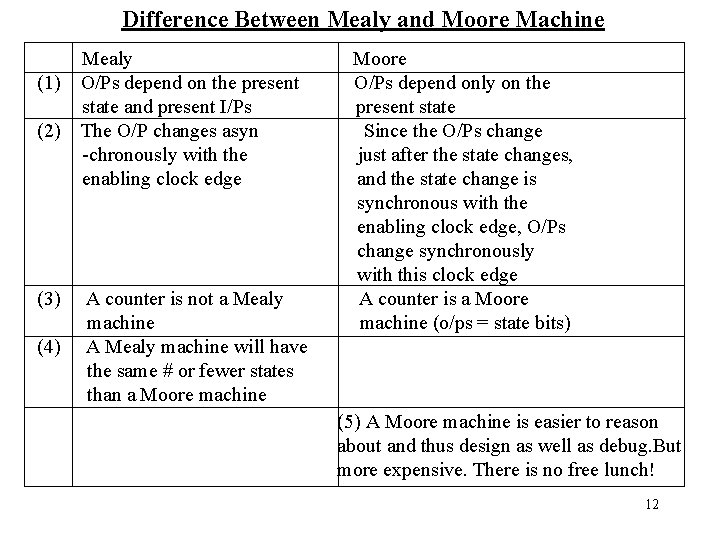
Difference Between Mealy and Moore Machine (1) (2) (3) (4) Mealy O/Ps depend on the present state and present I/Ps The O/P changes asyn -chronously with the enabling clock edge A counter is not a Mealy machine A Mealy machine will have the same # or fewer states than a Moore machine Moore O/Ps depend only on the present state Since the O/Ps change just after the state changes, and the state change is synchronous with the enabling clock edge, O/Ps change synchronously with this clock edge A counter is a Moore machine (o/ps = state bits) (5) A Moore machine is easier to reason about and thus design as well as debug. But more expensive. There is no free lunch! 12

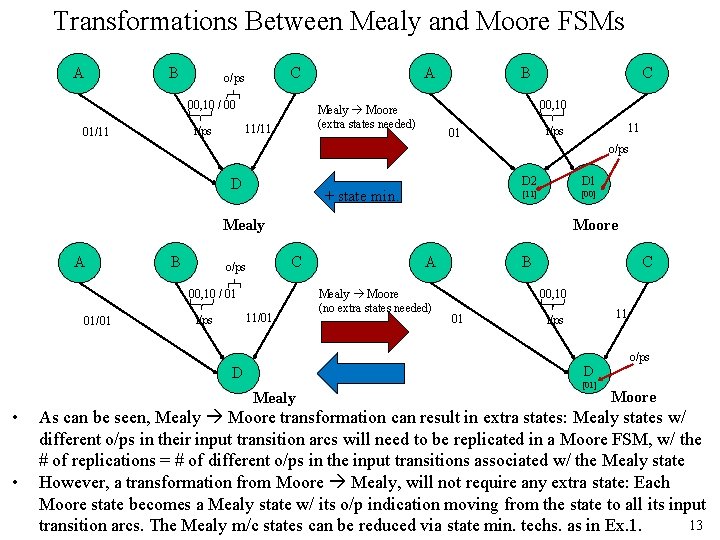
Transformations Between Mealy and Moore FSMs A B C o/ps 00, 10 / 00 B C 00, 10 Mealy Moore (extra states needed) 11/11 i/ps 01/11 A 11 i/ps 01 o/ps D + state min. D 2 D 1 [11] [00] Moore Mealy A B C o/ps 00, 10 / 01 01/01 11/01 i/ps Mealy • Mealy Moore (no extra states needed) B C 00, 10 01 11 i/ps D D • A [01] o/ps Moore As can be seen, Mealy Moore transformation can result in extra states: Mealy states w/ different o/ps in their input transition arcs will need to be replicated in a Moore FSM, w/ the # of replications = # of different o/ps in the input transitions associated w/ the Mealy state However, a transformation from Moore Mealy, will not require any extra state: Each Moore state becomes a Mealy state w/ its o/p indication moving from the state to all its input 13 transition arcs. The Mealy m/c states can be reduced via state min. techs. as in Ex. 1.

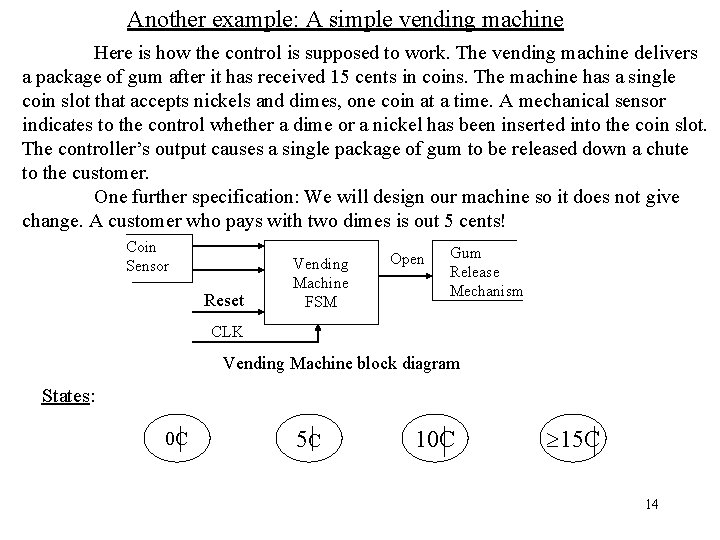
Another example: A simple vending machine Here is how the control is supposed to work. The vending machine delivers a package of gum after it has received 15 cents in coins. The machine has a single coin slot that accepts nickels and dimes, one coin at a time. A mechanical sensor indicates to the control whether a dime or a nickel has been inserted into the coin slot. The controller’s output causes a single package of gum to be released down a chute to the customer. One further specification: We will design our machine so it does not give change. A customer who pays with two dimes is out 5 cents! Coin Sensor Reset Vending Machine FSM Open Gum Release Mechanism CLK Vending Machine block diagram States: 0 C 5 C 10 C 15 C 14

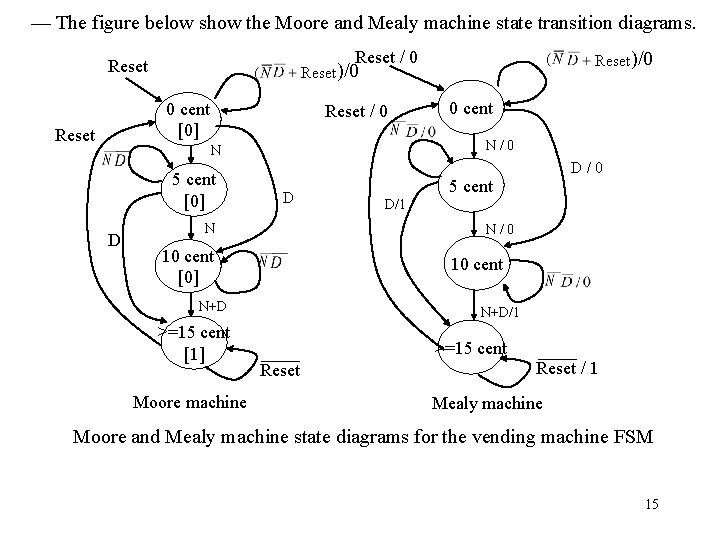
— The figure below show the Moore and Mealy machine state transition diagrams. Reset / 0 Reset 0 cent [0] Reset / 0 5 cent [0] D N 5 cent D/1 10 cent N+D Moore machine D/0 N/0 10 cent [0] >=15 cent [1] 0 cent N/0 N D Reset )/0 N+D/1 >=15 cent Reset / 1 Mealy machine Moore and Mealy machine state diagrams for the vending machine FSM 15

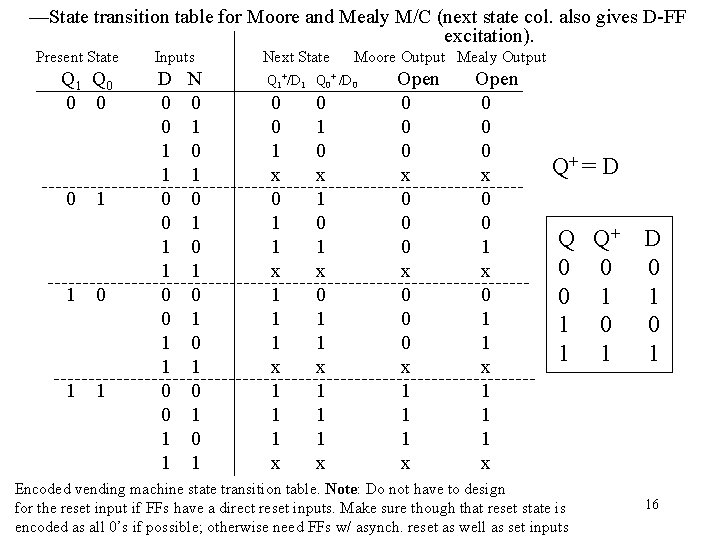
—State transition table for Moore and Mealy M/C (next state col. also gives D-FF excitation). Present State Q 1 Q 0 0 1 1 Inputs D 0 0 1 1 N 0 1 0 1 Next State Moore Output Mealy Output Q 1+/D 1 Q 0+ /D 0 0 0 1 x 0 1 1 x 1 1 1 x 0 1 0 x 1 0 1 x 0 1 1 x 1 1 1 x Open 0 0 0 x 1 1 1 x Open 0 0 0 x 0 0 1 x 0 1 1 x 1 1 1 x Q+ = D Q Q+ 0 0 0 1 1 Encoded vending machine state transition table. Note: Do not have to design for the reset input if FFs have a direct reset inputs. Make sure though that reset state is encoded as all 0’s if possible; otherwise need FFs w/ asynch. reset as well as set inputs D 0 1 16

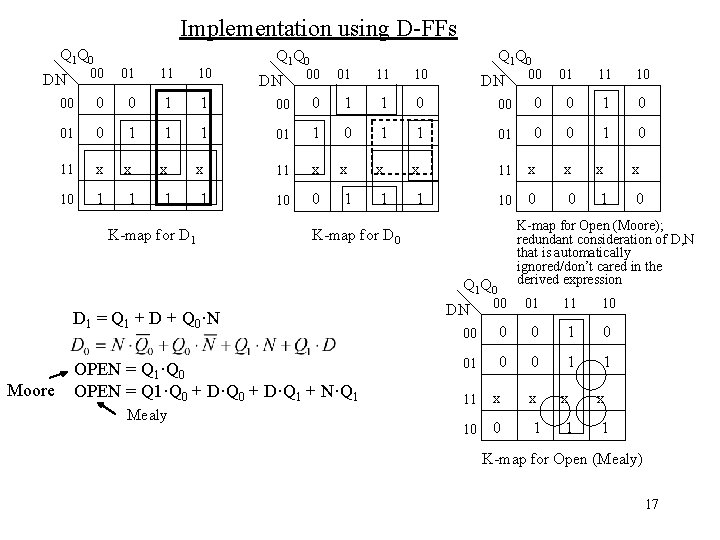
Implementation using D-FFs Q 1 Q 0 00 01 11 10 00 0 0 1 1 01 0 1 1 11 x x 10 1 1 DN Q 1 Q 0 00 01 11 10 00 0 1 1 01 1 0 1 x x 1 1 10 0 1 K-map for D 1 DN Q 1 Q 0 00 01 11 10 00 0 0 1 01 0 0 1 0 x x 11 x x 1 1 10 0 0 1 0 DN K-map for Open (Moore); redundant consideration of D, N that is automatically ignored/don’t cared in the derived expression K-map for D 0 Q 1 Q 0 D 1 = Q 1 + D + Q 0·N Moore OPEN = Q 1·Q 0 + D·Q 1 + N·Q 1 Mealy 00 01 11 10 00 0 0 1 1 DN 11 x x 10 0 1 1 1 K-map for Open (Mealy) 17

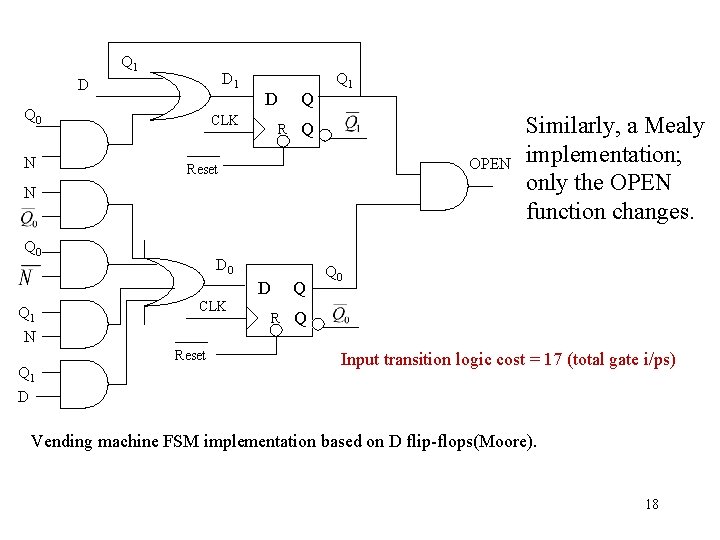
Q 1 D Q 0 N D CLK Q R Q 1 Q OPEN Reset N Q 0 D Q 1 N CLK Reset Q 1 D Q R Similarly, a Mealy implementation; only the OPEN function changes. Q 0 Q Input transition logic cost = 17 (total gate i/ps) Vending machine FSM implementation based on D flip-flops(Moore). 18

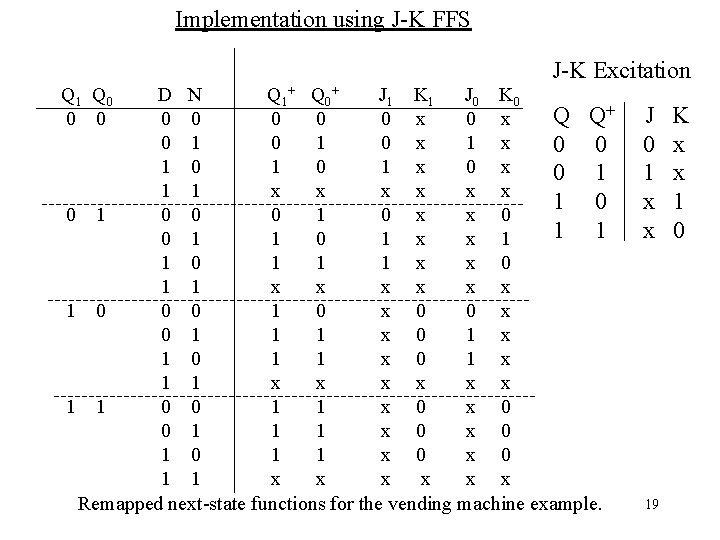
Implementation using J-K FFS Q 1 Q 0 0 0 J-K Excitation D N Q 1 + Q 0 + J 1 K 1 J 0 K 0 Q Q+ 0 0 0 x 0 1 0 x 1 x 0 0 1 0 1 x 0 1 1 1 x x x 1 0 0 0 1 0 x x 0 1 1 0 1 x x 1 1 0 1 1 1 x x 0 1 1 x x x 1 0 0 0 1 0 x 0 1 1 1 x 0 1 x 1 0 1 1 x 0 1 x 1 1 x x x 1 1 0 0 1 1 x 0 0 1 1 1 x 0 1 0 1 1 x x x Remapped next-state functions for the vending machine example. J 0 1 x x 19 K x x 1 0

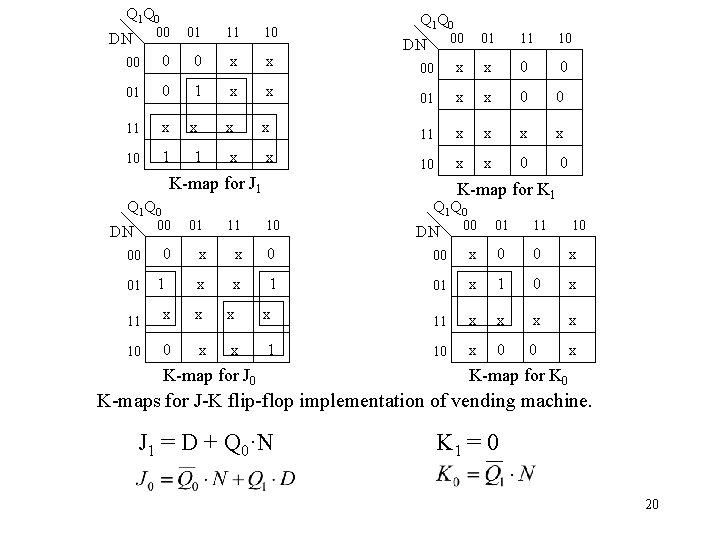
Q 1 Q 0 00 01 11 10 00 0 0 x x 01 0 1 x 11 x x 10 1 1 DN Q 1 Q 0 00 01 11 10 00 x x 0 0 x 01 x x 0 0 x x 11 x x x 10 x x 0 0 DN K-map for J 1 Q 1 Q 0 00 DN 00 01 0 1 01 11 K-map for K 1 10 Q 1 Q 0 DN 00 01 11 10 x x 0 00 x 0 0 x x x 1 01 x 1 0 x 11 x x x x 10 0 x x 1 10 x 0 0 x K-map for J 0 K-map for K 0 K-maps for J-K flip-flop implementation of vending machine. J 1 = D + Q 0·N K 1 = 0 20

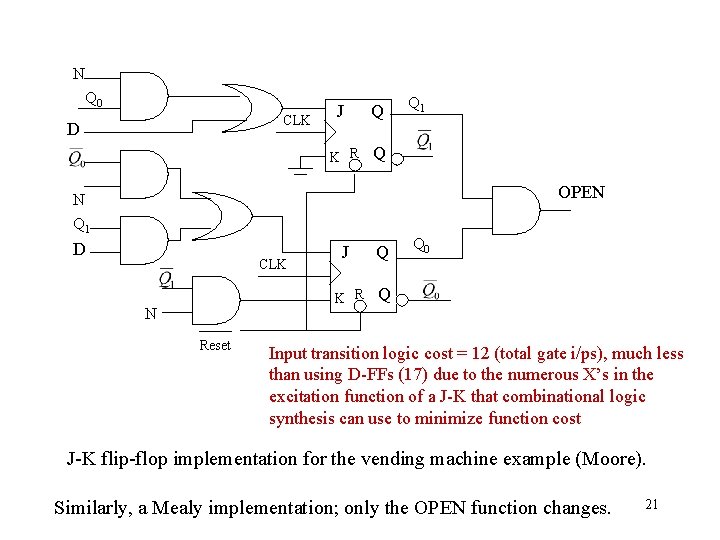
N Q 0 CLK D J Q K R Q Q 1 OPEN N Q 1 D CLK N Reset J Q K R Q Q 0 Input transition logic cost = 12 (total gate i/ps), much less than using D-FFs (17) due to the numerous X’s in the excitation function of a J-K that combinational logic synthesis can use to minimize function cost J-K flip-flop implementation for the vending machine example (Moore). Similarly, a Mealy implementation; only the OPEN function changes. 21

Basic Steps in the FSM Design Procedure (1 -3 mainly for Computational FSMs) 1. Understand the problem and determine the minimal # of different information classes about past i/ps required to solve it. 2. Convert these information classes into distinct states (which we informally call tentative states), and determine the state transition diagram of the FSM. 3. If the state transitions between states are well-defined (i. e. , for each state and i/p value, it is unambiguous what the next state should be), then these are the final states. • Otherwise, states from which transitions are not well defined need to be split into multiple states (called extra states) so that non-well-defined transitions are then translated to well-defined transitions between the “first” of these states and the remaining extra state(s), and also from the extra state(s) to other original states (see, e. g. , FSM prob. 1 next) 4. Determine the reset state 5. Perform state minimization 6. (a) Encode states in binary [optional—perform state assignment for logic minimization] (state bits) & obtain state transition table &FF excitation for desired FF type. Or (b) Implement a one-hot style seq. ckt in which each state is represented by a unique FSM 7. Minimize the output and FF excitation input functions (using K-Maps or QM, for example) and implement the FSM using these FFs and logic gates (or MUXes, 22 PLAs, PALs, etc. ).

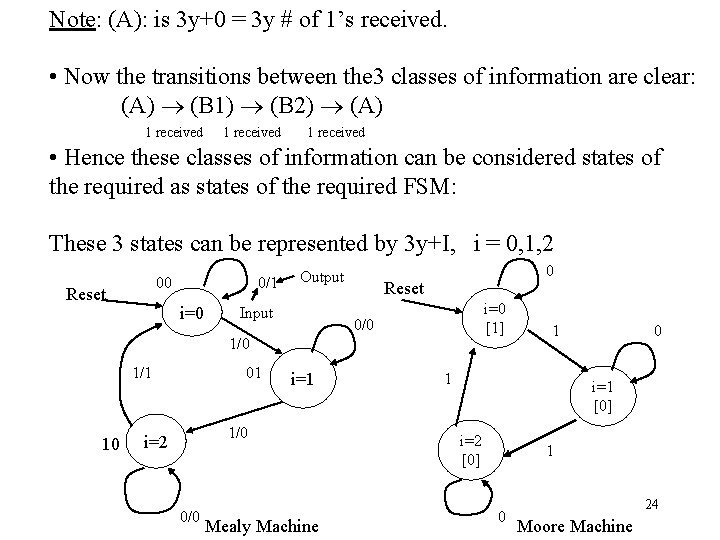
FSM Word Problem 1: • Design a system that outputs a ‘ 1’ whenever it receives a multiple of 3 # of 1’s (i. e. , 0, 3, 6, 9, etc. # of 1’s) on a serial input line x. — Relevant information classes needed to solve the problem: (A) A multiple of 3 # is received. (B) A non-multiple of 3 # is received. Questions to consider: (1) How do we go from (A) (B) Ans. : If a ‘ 1’ is received (2) How do we go from (B) (A) Ans. : Not clear. Need to split up (B) further into (B 1): 3 y+1 # of 1’s received. Where y is an integer 0. (B 2): 3 y+2 # of 1’s received. 23

Note: (A): is 3 y+0 = 3 y # of 1’s received. • Now the transitions between the 3 classes of information are clear: (A) (B 1) (B 2) (A) 1 received • Hence these classes of information can be considered states of the required as states of the required FSM: These 3 states can be represented by 3 y+I, i = 0, 1, 2 00 Reset 0/1 i=0 Output Input 0 Reset i=0 [1] 0/0 1/1 10 01 i=1 1/0 i=2 0/0 Mealy Machine 1 1 0 i=1 [0] i=2 [0] 1 0 24 Moore Machine

FSM Word Problem 2: • Design a system that outputs a ‘ 1’ whenever it receives: (a) A multiple of 3 # of 1’s AND (b) A non-zero even # of 0’s # of 1’s E. g. , ((0, 2) , (3, 4) , (6, 2) , ···) # of 0’s — Relevant classes of information: Use D&C to figure this out! - Break problem into relevant classes of # of 1’s & relevant classes of # of 0’s - For # of 1’s: 3 y+i, i = 0, 1, 2 [3 classes] - For # of 0’s: 2 z+j, j = 0, 1 For j = 0, we need to distinguish between zero (z = 0) and non-zero (z > 0) # of 0’s - Thus we have 3 classes: 2 z+0, z = 0 ( 0 ) 2 z+0, z > 0 ( non-zero even ) 25 2 z+1 ( odd )

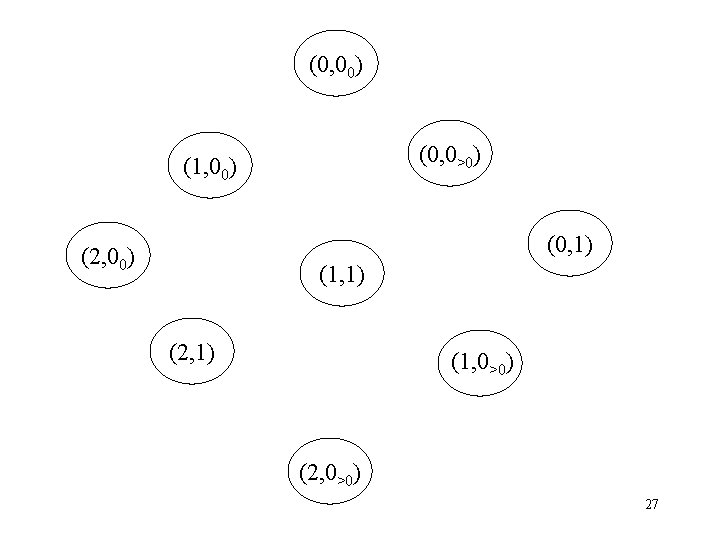
The relevant # of 1’s can be represented by i = { 0, 1, 2 } ( # of 1’s = 3 y+i ) — The relevant # of 0’s can be represented by j= { 00 , 0>0 , 1 } ( # of 0’s = 2 z+j ) where the subscript of the 0 indicates whether z=0 or z>0. — Since at any point time, a certain # of 1’s and # of 0’s will have been received, the state of the system will be given by a combination of relevant # of 1’s and # of 0’s. — There are 9 combinations: { 0, 1, 2, } X { 00, 0>0, 1 } = (0, 00), (0, 0>0), (0, 1), (1, 00), (1, 0>0), (1, 1), (2, 00), (2, 0>0), (2, 1) # of 1’s # of 0’s Cartesian Product 26

(0, 00) (0, 0>0) (1, 00) (0, 1) (2, 00) (1, 1) (2, 1) (1, 0>0) (2, 0>0) 27

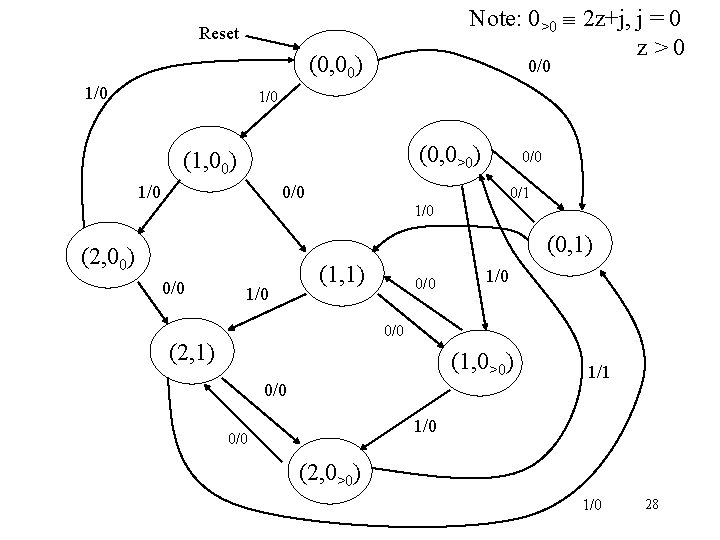
Note: 0>0 2 z+j, j = 0 z>0 Reset (0, 00) 1/0 0/0 1/0 (0, 0>0) (1, 00) 1/0 0/0 0/1 1/0 (0, 1) (2, 00) 0/0 1/0 (1, 1) 0/0 1/0 0/0 (2, 1) (1, 0>0) 0/0 1/1 1/0 0/0 (2, 0>0) 1/0 28

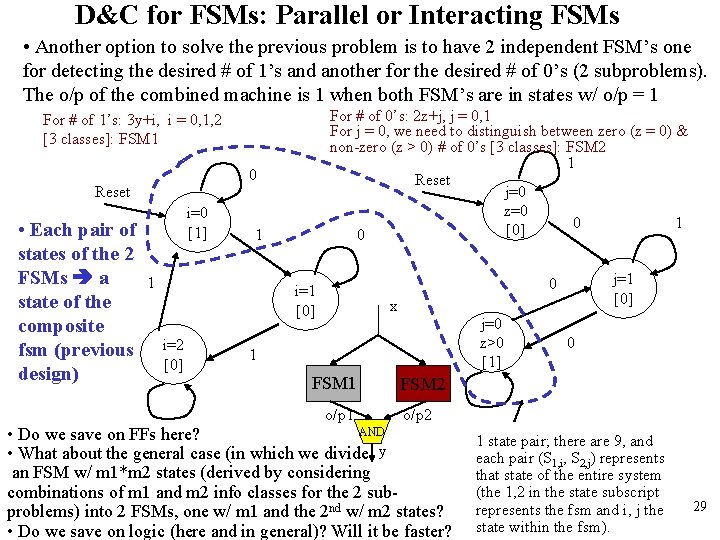
D&C for FSMs: Parallel or Interacting FSMs • Another option to solve the previous problem is to have 2 independent FSM’s one for detecting the desired # of 1’s and another for the desired # of 0’s (2 subproblems). The o/p of the combined machine is 1 when both FSM’s are in states w/ o/p = 1 For # of 0’s: 2 z+j, j = 0, 1 For j = 0, we need to distinguish between zero (z = 0) & non-zero (z > 0) # of 0’s [3 classes]: FSM 2 1 Reset j=0 z=0 0 1 [0] 0 For # of 1’s: 3 y+i, i = 0, 1, 2 [3 classes]: FSM 1 0 Reset • Each pair of states of the 2 FSMs a state of the composite fsm (previous design) i=0 [1] 1 1 i=2 [0] j=1 [0] 0 i=1 [0] x j=0 z>0 [1] 1 FSM 1 0 FSM 2 o/p 1 o/p 2 • Do we save on FFs here? • What about the general case (in which we divide y an FSM w/ m 1*m 2 states (derived by considering combinations of m 1 and m 2 info classes for the 2 subproblems) into 2 FSMs, one w/ m 1 and the 2 nd w/ m 2 states? • Do we save on logic (here and in general)? Will it be faster? AND 1 state pair; there are 9, and each pair (S 1, i, S 2, j) represents that state of the entire system (the 1, 2 in the state subscript represents the fsm and i, j the state within the fsm). 29

D&C for FSMs: Parallel or Interacting FSMs (contd) • Q: When can a single FSM design be decomposed into >= 2 simpler fsm’s? • Answer: 1. When the compound o/p condition can be decomposed into multiple smaller independent/nonoverlapping o/p conditions (as in this example). In such a case, these smaller conditions (equivalently, sub-problems) can each be determined by a simpler fsm. Each of these simpler fsm’s o/ps are used to determine the final o/p via stitch-up logic that corresponds to how the multiple smaller o/p conditions are logically composed (or “connected”) to form the original o/p condition. 2. Or, in general, we can use D&C to decompose the problem into smaller non-overlapping parallel sub-problems (which may not all be the same type) and stitch them up, as we saw for the D&C of combinational circuits. E. g. , Problem: System needs to o/p a 1 when a multiple of 6 1’s has been seen. Can this be decomposed into smaller problems? 3. Or, decompose into overlapping sequential/dependent sub-problems. How to decompose the problem of detecting multiple of 9 1’s? 30

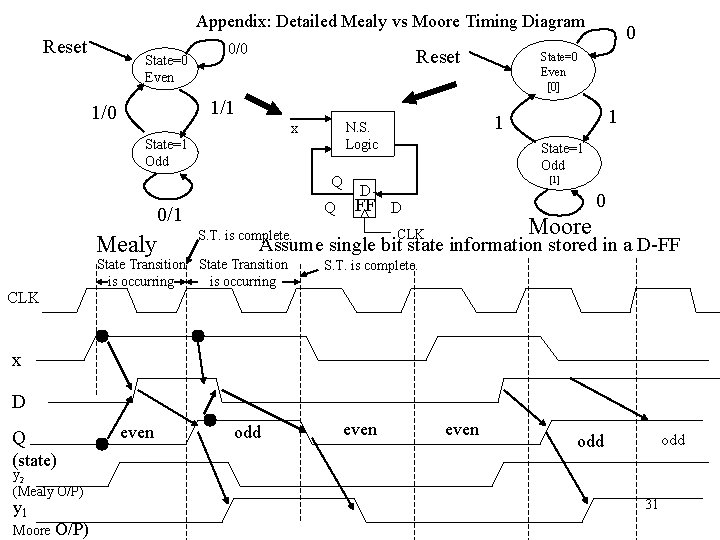
Appendix: Detailed Mealy vs Moore Timing Diagram Reset State=0 Even 0/0 Reset 1/1 1/0 State=1 Odd Q Q 0/1 Mealy [1] D- 0 Moore CLK Assume single bit state information stored in a D-FF State Transition is occurring CLK 1 State=1 Odd FF D S. T. is complete. State=0 Even [0] 1 N. S. Logic x 0 S. T. is complete. x D even Q (state) y 2 (Mealy O/P) y 1 Moore O/P) odd even odd 31