Differential Equations MTH 242 Lecture 12 Dr Manshoor









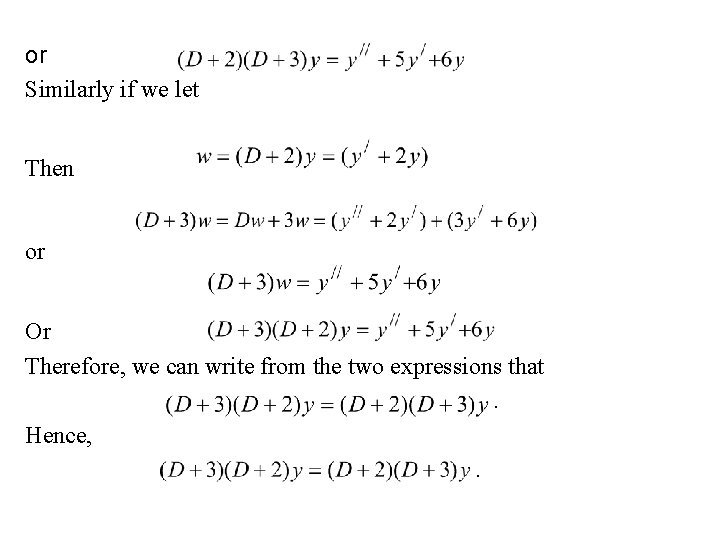





























- Slides: 39

Differential Equations MTH 242 Lecture # 12 Dr. Manshoor Ahmed

Summary (Recall)


Higher order derivatives in terms of the operator . Similarly, • The following polynomial expression of degree operator involving the is also a linear differential operator. Here, the following expressions are all linear differential operators

Differential Equation in Terms of D: Any linear differential equation can be expressed in terms of the notation. Consider a 2 nd order equation with constant coefficients Since Thus, one can write the equation as or Now, we define another differential operator as

Then, the equation can be written in compact form as The operator is a second-order linear differential operator with constant coefficients. Example 1: Consider the differential equation. Since, . Therefore, we get In the operator form we can write the equation as

Then the given differential can be compactly written as Example 2: Apply the operator Solution: - to the function

Factorization of a differential operator: • An nth-order linear differential operator with constant coefficients can be factorized, whenever the characteristics polynomial equation can be factorized. • The factors of a linear differential operator with constant coefficients commute. Example 1: (a) Consider the following 2 nd order linear differential operator

If we treat as an algebraic quantity, then the operator can be factorized as (b) To illustrate the commutative property of the factors, we consider a twice-differentiable function. Then we can write To verify this we let Then or or
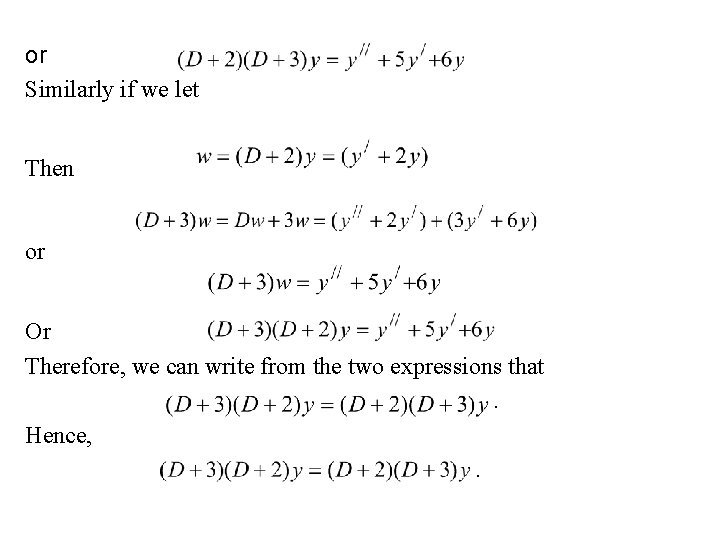
or Similarly if we let Then or Or Therefore, we can write from the two expressions that. Hence, .

Example 2: (a). The operator can be factorized as Or (b). The operator Example 3: The differential equation can be written as or does not factor with real numbers.

Or Annihilator Operator: Suppose that • L is a linear differential operator with constant coefficients. • y = f(x) defines a sufficiently differentiable function. • The function f is such that Then the differential operator L is said to be an annihilator operator of the function f. Example 4: Since Therefore, the differential operators

are annihilator operators of the following functions In general, the differential operator functions annihilates each of the Hence, we conclude that the polynomial function can be annihilated by finding an operator that annihilates the highest power of Example 5: Find a differential operator that annihilates the polynomial function

Solution : Since Therefore Hence, is the differential operator that annihilates the function Remark: The functions that are annihilated by an nth-order linear differential operator are simply those functions that can be obtained from the general solution of the homogeneous differential equation

Example 6: Consider the homogeneous linear differential equation of order n The auxiliary equation of the differential equation is Therefore, the auxiliary equation has a real root of multiplicity. So that the differential equation has the following linearly independent solutions. Therefore, the general solution of the differential equation is So that the differential operator

annihilates each of the functions Hence, as a consequence of the fact that the differentiation can be performed term by term, the differential operator annihilates the function Example 7: Find an annihilator operator for the functions (a). (b).

Solution (a) Since Therefore, the annihilator operator of function f is given by We notice that in this case (b) Similarly or or

Therefore, the annihilator operator of the function is given by We notice that in this case Example 8: Consider the differential equation The auxiliary equation is Therefore formula , when are real numbers, we have from the quadratic Therefore, the auxiliary equation has the following two complex roots of multiplicity n.

Thus, the general solution of the differential equation is a linear combination of the following linearly independent solutions Hence, the differential operator is the annihilator operator of the functions

Example 9: If we take Then the differential operator becomes Also, it can be verified that Therefore, the linear differential operator annihilates the functions

Now, consider the differential equation The auxiliary equation is Therefore, the functions are the two linearly independent f solutions of the differential equation

Therefore, the operator also annihilates a linear combination of and , e. g. Example 10: If we take Then the differential operator Becomes Also, it can be verified that

and Therefore, the linear differential operator annihilates the functions

Important result: • If a linear differential operator with constant coefficients is such that i. e. the operator annihilates the functions and operator annihilates their linear combination. . Then the This result follows from the linearity property of the differential operator. • Suppose that and are linear operators with constant coefficients such that and

then the product of these differential operators linear sum annihilates the So that To demonstrate this fact we use the linearity property for writing Since Therefore Or But we know that

Therefore Example 11: Find a differential operator that annihilates the function Solution: Suppose that Then Therefore, annihilates the function

Example 12: Find a differential operator that annihilates the function Solution Suppose that Then Therefore, the product of two operators annihilates the given function

Solution of the non-homogeneous DE by Annihilator operator method











Summary • Differential Operator, which is a linear operator. • Differential equation in linear operator form. • Auxiliary equation in terms of differential operator form. • Annihilator operators of different functions. • Solution non-homogeneous equation with annihilator operator.
 Calculus with analytic geometry examples
Calculus with analytic geometry examples Mth 105
Mth 105 Mth 685
Mth 685 Mth
Mth Mth 685
Mth 685 Mth 210
Mth 210 Mth 210
Mth 210 Mth 685
Mth 685 01:640:244 lecture notes - lecture 15: plat, idah, farad
01:640:244 lecture notes - lecture 15: plat, idah, farad Schema 242
Schema 242 Santa paz e alegria la no ceu vou desfrutar
Santa paz e alegria la no ceu vou desfrutar Fpunity
Fpunity Sxvisi saxli
Sxvisi saxli Lagu muliakan allah bapa
Lagu muliakan allah bapa Me 242
Me 242 Et 242
Et 242 He 242
He 242 Step ap 242
Step ap 242 Gezang 242
Gezang 242 I^242
I^242 Algol family
Algol family Carelli kutztown
Carelli kutztown Et 242
Et 242 49 cfr part 242
49 cfr part 242 Is-242.b
Is-242.b Vip room standard life
Vip room standard life L
L Derivation of maxwell's equations in differential form
Derivation of maxwell's equations in differential form Pde paula
Pde paula Adam moulton method
Adam moulton method Differential equations variation of parameters
Differential equations variation of parameters Highest order chapter 1
Highest order chapter 1 Bernoulli equation differential equations examples
Bernoulli equation differential equations examples What is a first order equation
What is a first order equation Midpoint method formula
Midpoint method formula Differential equation
Differential equation First order pde method of characteristics
First order pde method of characteristics Differential equations summary
Differential equations summary Higher order linear differential equations
Higher order linear differential equations Exponential differential equation
Exponential differential equation