Differential Equations MTH 242 Lecture 10 Dr Manshoor

Differential Equations MTH 242 Lecture # 10 Dr. Manshoor Ahmed

Summary (Recall) • Solution of Higher order linear differential equation. • Solution of homogeneous equations. • Superposition principle. • Linearly independent Solutions. • Fundamental set of solutions, general solution. • Solution of non-homogeneous equations. • Complementary function and particular solution.

Constructing a second solution from a known solution

Constructing a second solution from a known solution General case: The general, 2 nd order, linear homogenous differential equation is Dividing throughout by and let , We get , where P(x) and Q(x) are continuous on some interval I.

Constructing a second solution from a known solution Suppose that We define then Since This implies that we must have

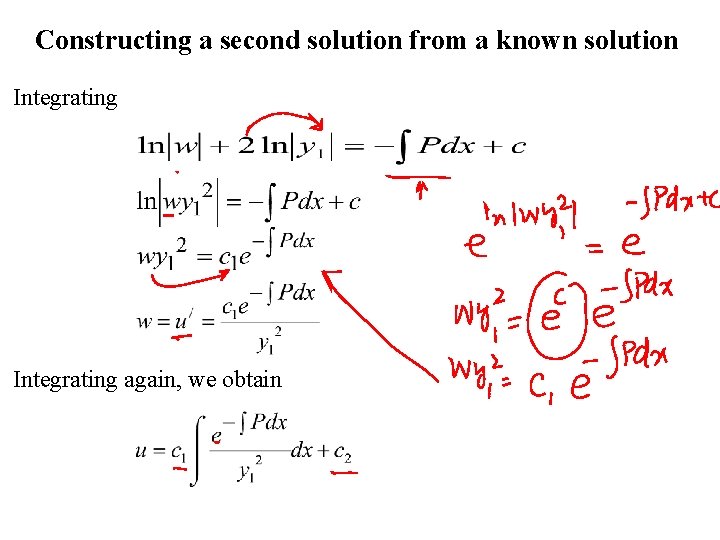
Constructing a second solution from a known solution This implies that we must have If we suppose then The equation is separable. Separating variables we have from the last equation

Constructing a second solution from a known solution Integrating again, we obtain

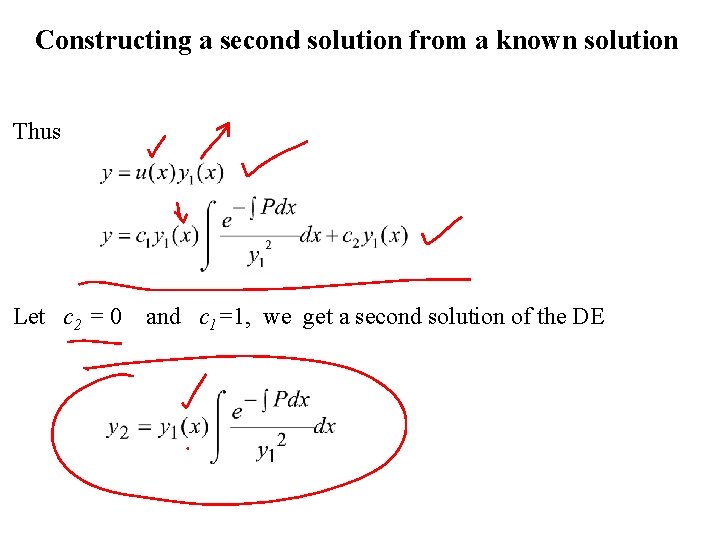
Constructing a second solution from a known solution Thus Let c 2 = 0 and c 1=1, we get a second solution of the DE

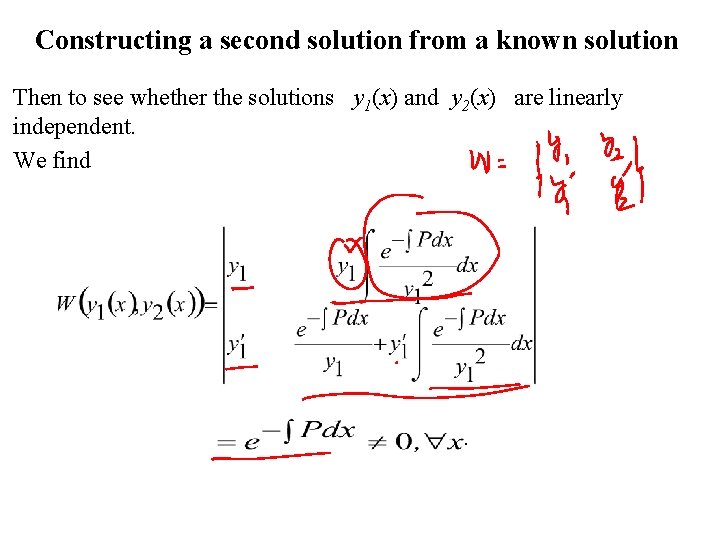
Constructing a second solution from a known solution Then to see whether the solutions y 1(x) and y 2(x) are linearly independent. We find .

Constructing a second solution from a known solution Therefore y 1(x) and y 2(x) are linear independent set of solutions. So that they form a fundamental set of solutions of the differential equation Hence, the general solution of the DE is Example 1: Given that is a solution of. Find general solution of the differential equation on the interval.

Constructing a second solution from a known solution Solution: The equation can be written as The 2 nd solution or y 2 is given by

Constructing a second solution from a known solution Hence the general solution of the differential equation on by or Example 2: Verify that is a solution of on . Find a second solution of the equation. is given

Constructing a second solution from a known solution Solution: The differential equation can be written as The 2 nd solution is given by

Constructing a second solution from a known solution Therefore, Thus the second solution is. Hence, general solution of the differential equation is

Constructing a second solution from a known solution Reduction of Order: For a linear 2 nd order differential equation , we can construct a second solution from a known solution. Suppose y 1(x) is a non zero solution of the equation We assume that the coefficient s of the above equation are continuous an for every x in some interval I. The process we use to find a second solution y 2(x) consists of reducing the order of equation to a 1 st order equation. Example: Given a differential equation having y 1 = ex as one solution.

Constructing a second solution from a known solution Now we have to determine y 2(x) Let us take then By substituting in the given equation we get Since implies

Constructing a second solution from a known solution Now let Thus we have Using the integrating factor Multiplying both sides of above equation by integrating factor and solving we get or

Constructing a second solution from a known solution Integrating we get Thus Let c 2=0 we get and c 1 = -2 which is the second solution of the given differential equation.

Constructing a second solution from a known solution Now to check whether the solution is independent or not for every x, the solution are linearly independent on thus This is the general solution of the given equation.

Solution of homogeneous linear DE with constant coefficients

Homogeneous linear equations with constant coefficients As the linear first order equation where a is a constant, has the exponential solution on Now for higher order equations All solutions of equation are exponential functions or constructed out of exponential functions.

Homogeneous linear equations with constant coefficients SPECIAL CASE Consider the case of second order equation. Let solution be of the form Then, and Plugin these values into the current eq. or As

Homogeneous linear equations with constant coefficients

Homogeneous linear equations with constant coefficients Example 1 Solve the following differential equation Solution Put Then Substituting in the given differential equation we get As So

Homogeneous linear equations with constant coefficients The roots of the equation are Thus the general solution is

Homogeneous linear equations with constant coefficients Example 2 Solve the following differential equation Solution Auxiliary equation is , thus

Homogeneous linear equations with constant coefficients Case 2 When roots of equation are real and equal, that is only one solution is obtained Second solution for this case is From quadratic formula

Homogeneous linear equations with constant coefficients Therefore, thus The general solution of equation is then

Homogeneous linear equations with constant coefficients Example 1 Solve the differential equation Solution Put Then Substituting in the given differential equation we get As Thus So

Homogeneous linear equations with constant coefficients Example 2 Solve the differential equation Auxiliary equation is Which is the general solution of the given differential equation.

Homogeneous linear equations with constant coefficients Case 3 If m 1 and m 2 are complex then and Where hence and are real and i 2 = -1 which is similar to case 1 and To convert into real function, we use Euler’s Formula where is any real number. It follows that

Homogeneous linear equations with constant coefficients and So and Since is solution of the differential equation for any constants c 1 and c 2 For and for

Homogeneous linear equations with constant coefficients Simplification gives and We can drop constant to write Hence, the general solution of the differential equation is

Homogeneous linear equations with constant coefficients Example 1 Solve the differential equation Put Then Substituting in the given differential equation we have Since, The auxiliary equation is

Homogeneous linear equations with constant coefficients Therefore, the auxiliary equation has the complex roots Hence, the general solution of the equation is

Homogeneous linear equations with constant coefficients Example 2 Solve the differential equation Auxiliary equation is The roots of this equation are The general solution is

Summary • Construction of 2 nd solution from a known solution. • Reduction of order. • How to solve a homogeneous linear differential with constant coefficients? • Auxiliary or characteristics equation. • How to write the general of solution of linear differential with constant coefficients