Differential Equations MTH 242 Lecture 03 Dr Manshoor




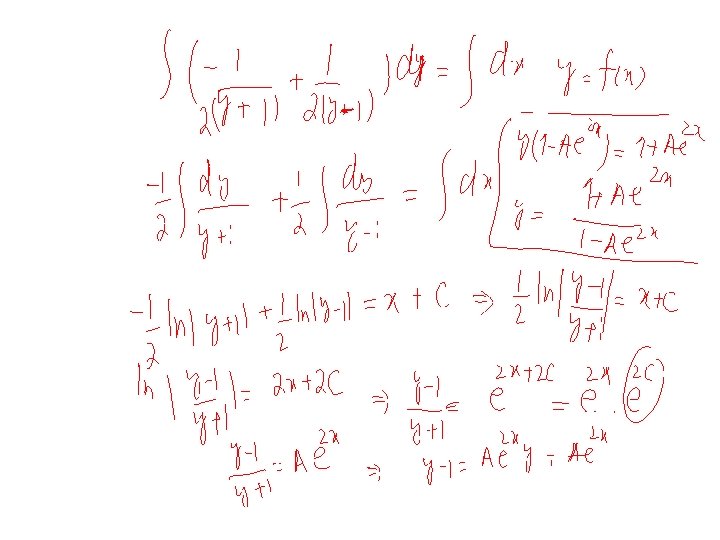


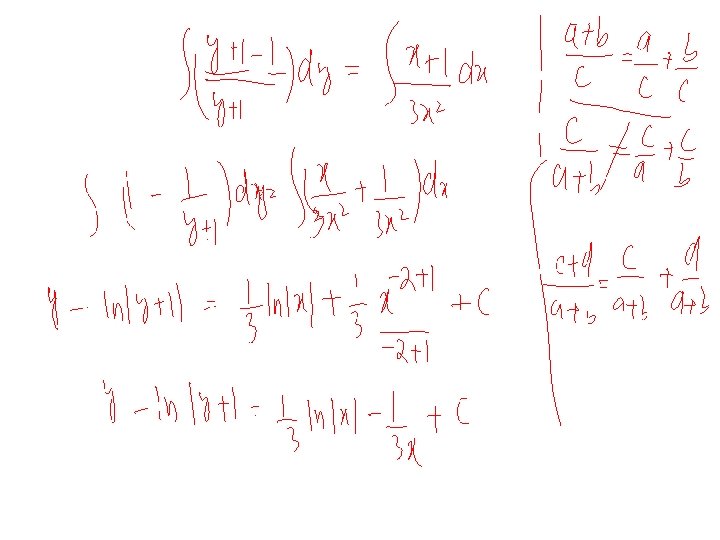
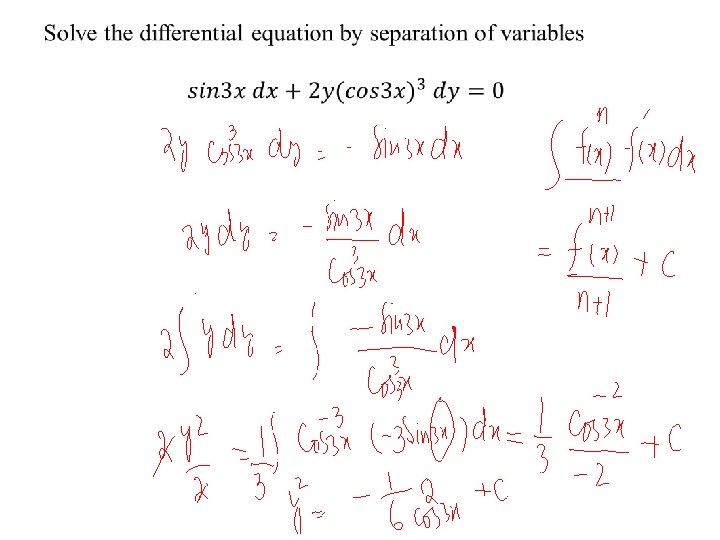








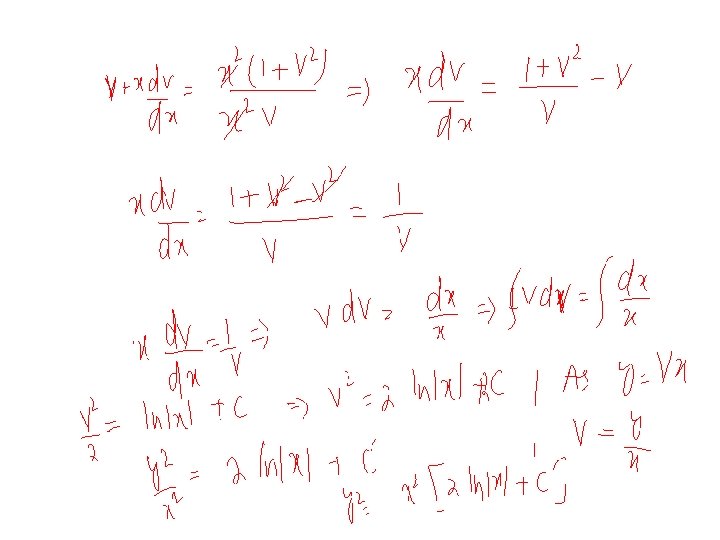

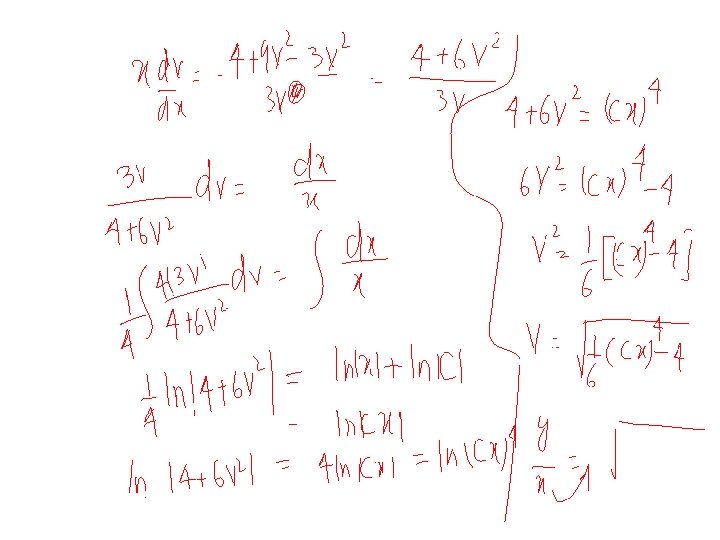









- Slides: 29

Differential Equations MTH 242 Lecture # 03 Dr. Manshoor Ahmed

Summary (Recall) • Solution of differential equation. • Interval of the solution. • Trivial, general, particular and singular Solutions. • Families of solutions. • Initial Value Problems. • Existence and uniqueness theorem.

First Order ODEs .

Solution of separable equation
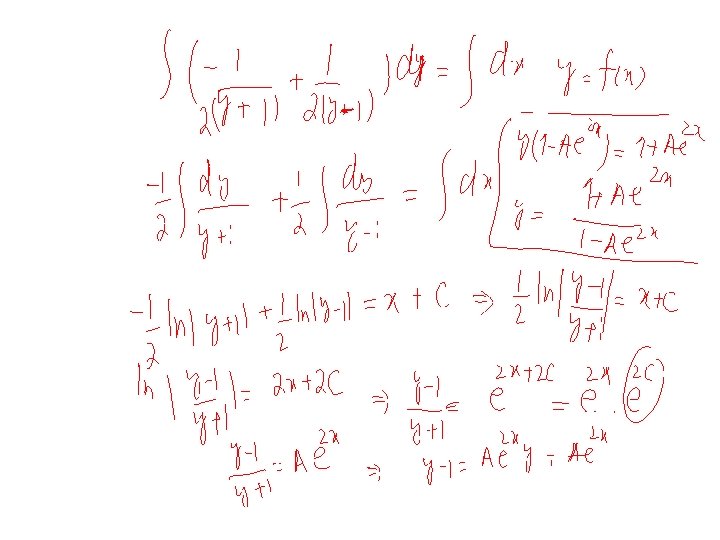


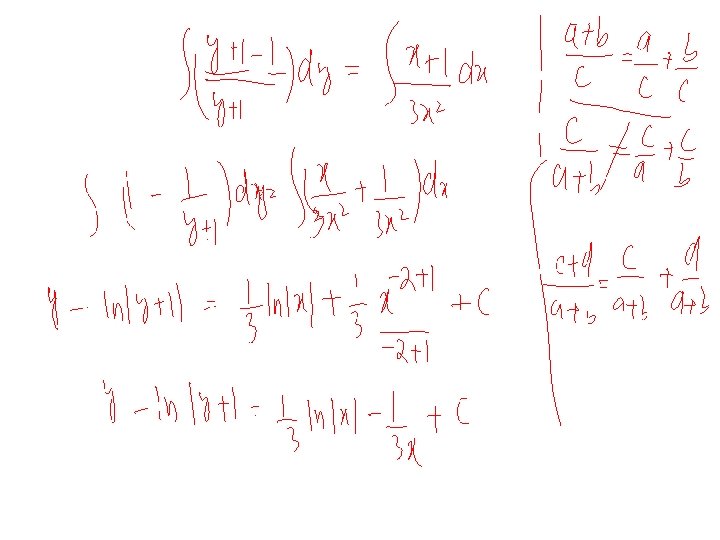
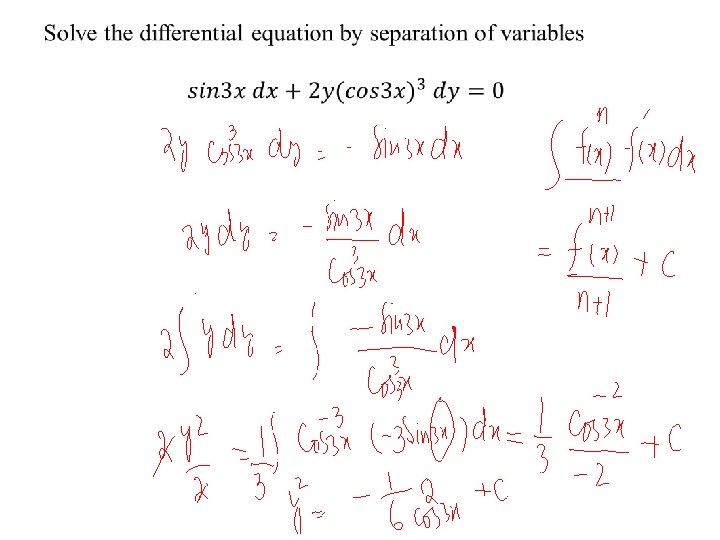

An initial value problem

Solve the initial value problem

Homogeneous function

Example 2 Example 3 13


Homogeneous Differential Equation

Method of solution

Solution of problems
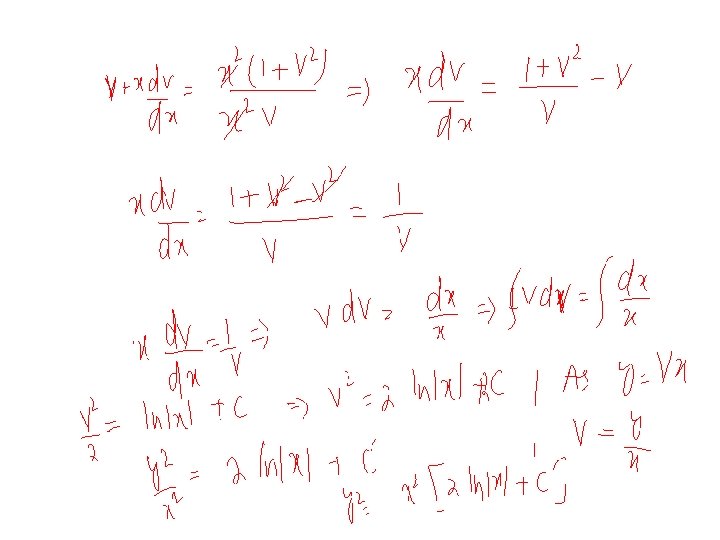

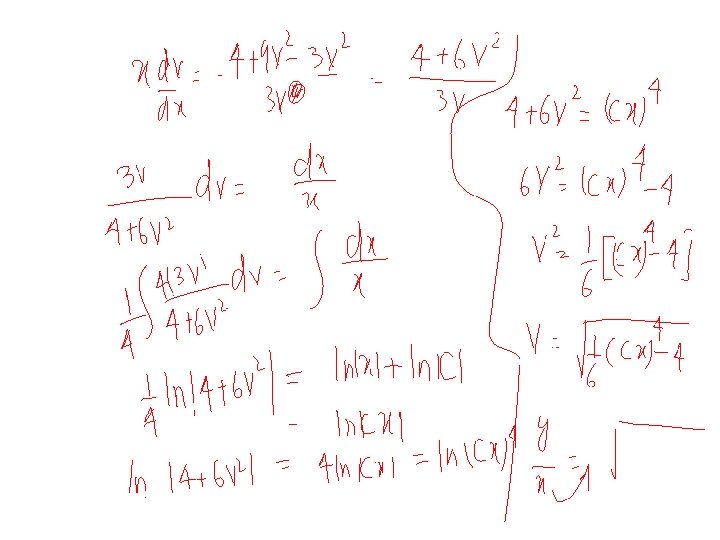

Equations reducible to homogenous form The differential equations is not homogenous. However, it can be reduced to a homogenous form as detailed below Case 1: We use the substitution which reduces the equation to a separable equation in the variables x & z. Solving the resulting separable equation and replacing z with , we obtain the solution of the given differential equation. 21

Case 2: In this case we substitute where h and k are constants to be determined. Then the equation Becomes We choose h and k such that 22

which reduces the equation to which is homogenous differential equation in X and Y, and can be solved accordingly. After having solved the last equation we come back to the old variables x and y. 23

Example Solve the differential equation Solution: Since , we substitute , so that Thus the equation becomes i. e. which is a variable separable form, and can be written as 24

Integrating both sides we get Simplifying and replacing z with , we obtain or 25

Example 4 Solve the differential equation Solution: By substitution The given differential equation reduces to We choose h and k such that Solving these equations we have h=2 , k=1. Therefore, we have which is a homogenous equation. 26

We substitute to obtain or Resolving into partial fractions and integrating both sides we obtain or Now substituting we get , , and simplifying 27


Summary • Separable differential equation. • Homogeneous function and homogeneous differential equation. • Equations reducible to homogeneous.
 Mth 685
Mth 685 Mth 210
Mth 210 Mth 210
Mth 210 Mth 685
Mth 685 Mth 104
Mth 104 Mth 105
Mth 105 Mth 685
Mth 685 Mth
Mth 01:640:244 lecture notes - lecture 15: plat, idah, farad
01:640:244 lecture notes - lecture 15: plat, idah, farad Gezang 239
Gezang 239 Hibbeler
Hibbeler Ac network theorems
Ac network theorems Csc 242
Csc 242 Step ap 242
Step ap 242 49 cfr part 242
49 cfr part 242 I^242
I^242 Algol typing discipline
Algol typing discipline Et 242
Et 242 Eu confio firmemente
Eu confio firmemente Is-242.b
Is-242.b Manulife vip room withdrawal
Manulife vip room withdrawal Lagu muliakan allah bapa
Lagu muliakan allah bapa Schema 242
Schema 242 Carrsh
Carrsh Series parallel resonance
Series parallel resonance Sxvisi cxovreba
Sxvisi cxovreba Calculus equation example
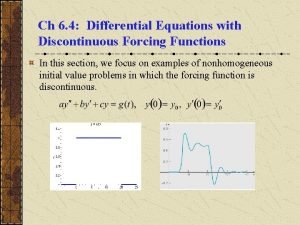
Calculus equation example Differential equations with discontinuous forcing functions
Differential equations with discontinuous forcing functions Cengage differential equations
Cengage differential equations Ordinary differential equations example
Ordinary differential equations example