CSE 246 Computer Arithmetic Algorithms and Hardware Design



![Full Adder o o o The inputs are x[i], y[i] (operand bits) and c[i] Full Adder o o o The inputs are x[i], y[i] (operand bits) and c[i]](https://slidetodoc.com/presentation_image_h2/9a1f40e2c09749b9d2bf077417c9e6fa/image-4.jpg)

![Ripple Carry Adder x[n-1] y[n-1] x[0] y[0] cin/c[0] y[1] c[n-1] . . . c[1] Ripple Carry Adder x[n-1] y[n-1] x[0] y[0] cin/c[0] y[1] c[n-1] . . . c[1]](https://slidetodoc.com/presentation_image_h2/9a1f40e2c09749b9d2bf077417c9e6fa/image-6.jpg)





![Ling’s Adder c[i] = g[i-1] + p[i-1]. g[i-2] + p[i-1]. p[i-2]. g[i 3] + Ling’s Adder c[i] = g[i-1] + p[i-1]. g[i-2] + p[i-1]. p[i-2]. g[i 3] +](https://slidetodoc.com/presentation_image_h2/9a1f40e2c09749b9d2bf077417c9e6fa/image-15.jpg)
![Ling’s Adder h[0]=c[0] h[3]=g[2]+g[1]+t[1]g[0]+t[1]t[0]h[0] s[3]=p[3]^c[3]=p[3]^(h[3]t[2]) =t[3]’h[3]t[2]+t[3](h[3]’+t[2]’) =h[3]’p[3]+h[3](p[3]^t[2]) h[6]=g[5]+g[4]+t[4]g[3]+t[4]t[3]t[2]h[3] s[6]=h[6]’p[6]+h[6]’(p[6]^t[5]) CSE 246 16 Ling’s Adder h[0]=c[0] h[3]=g[2]+g[1]+t[1]g[0]+t[1]t[0]h[0] s[3]=p[3]^c[3]=p[3]^(h[3]t[2]) =t[3]’h[3]t[2]+t[3](h[3]’+t[2]’) =h[3]’p[3]+h[3](p[3]^t[2]) h[6]=g[5]+g[4]+t[4]g[3]+t[4]t[3]t[2]h[3] s[6]=h[6]’p[6]+h[6]’(p[6]^t[5]) CSE 246 16](https://slidetodoc.com/presentation_image_h2/9a1f40e2c09749b9d2bf077417c9e6fa/image-16.jpg)


















- Slides: 56

CSE 246: Computer Arithmetic Algorithms and Hardware Design Lecture 4: Adders Instructor: Prof. Chung-Kuan Cheng CSE 246

Topics: o Adders n n n CSE 246 AND/OR gate v. s. Circuit Logic Design Graph Design (Prefix Adder) 2

Chapter 2: ADDERS o Half Adders n n n Half adders can add two 1 -bit binary numbers when there is no carry in. If the inputs are xi and yi, the sum and carry-out is given by the formula o si = x i ^ y i o ci+1 = xi. yi We use the following notations throughout the slides o. means logical AND o + means logical OR o ^ means logical XOR o ‘ means complementation CSE 246 3
![Full Adder o o o The inputs are xi yi operand bits and ci Full Adder o o o The inputs are x[i], y[i] (operand bits) and c[i]](https://slidetodoc.com/presentation_image_h2/9a1f40e2c09749b9d2bf077417c9e6fa/image-4.jpg)
Full Adder o o o The inputs are x[i], y[i] (operand bits) and c[i] (carry in) The outputs are s[i] (result bit) and c[i+1] (carry out) Inputs and outputs are related by these relations n n CSE 246 s[i] = x[i] ^ y[i] ^ c[i] c[i+1] = x[i]. y[i] + c[i]. (x[i] + y[i]) = x[i]. y[i] + c[i]. (x[i] ^ y[i]) 4

Full Adder o o If carry-in bit is zero, then full adder becomes half adder If carry-in bit is one, then n n o s[i] = (x[i] ^ y[i])’ c[i+1] = x[i] + y[i] To add two n-bit numbers, we can chain n full adders to build a ripple carry adder CSE 246 5
![Ripple Carry Adder xn1 yn1 x0 y0 cinc0 y1 cn1 c1 Ripple Carry Adder x[n-1] y[n-1] x[0] y[0] cin/c[0] y[1] c[n-1] . . . c[1]](https://slidetodoc.com/presentation_image_h2/9a1f40e2c09749b9d2bf077417c9e6fa/image-6.jpg)
Ripple Carry Adder x[n-1] y[n-1] x[0] y[0] cin/c[0] y[1] c[n-1] . . . c[1] c[2] cout s[n-1] s[0] Overflow happen when operands are of same sign, and the result is of different sign. If we use 2’s complement to represent negative numbers, overflow occurs when (cout ^ c[n-1]) is 1 CSE 246 6

Ripple Carry Adder o o o For sake of brevity, we use the following notations: n g[i] = x[i]. y[i] n p[i] = x[i] + y[i] In terms of these notations, we can rewrite carry equations as n c[1] = g[0] + p[0]. c[0] n c[2] = g[1] + p[1]. c[1] n and so on… n We shall use these notations afterwards while discussing the design of other kind of adders It has been observed that expected length of carry chain is 2, while expected maximal length of carry chain is lg n. Hence, ripple carry adders are in general fast. CSE 246 7

Ripple Carry Adder o How do know that an adder has completed the operation? n Worst case scenario: Wait for the longest chain in the carry propagation network n We might inspect c[i+1] and its complement b[i+1] to determine the status of the adder CSE 246 c[i+1] b[i+1] Remark 0 0 Not complete 1 0 Complete 0 1 Complete 1 1 Don’t care 8

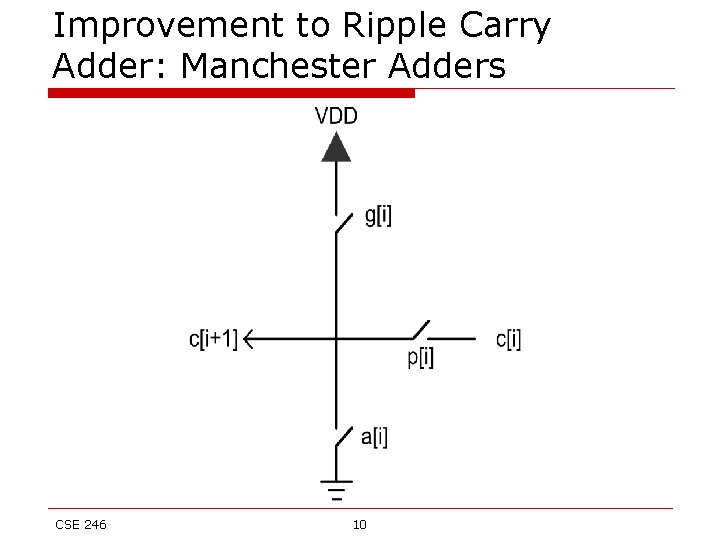
Improvement to Ripple Carry Adder: Manchester Adders o o o By intelligently using our device properties, we can reduce the complexity of the circuit used to compute carries in a ripple carry adder. Define: a[i] = (x[i])’. (y[i])’ Next we observe that c[i+1] is 1 in exactly these scenarios: n g[i] is 1, i. e. both x[i] & y[i] are 1 n c[i] is 1 and it is propagated because p[i] is 1 c[i+1] is ‘pulled down’ to logic 0 irrespective of the value of c[i], when a[i] is 1, i. e. both x[i] and y[i] are 0 From these conditions, and keeping in mind the general characteristics of transistor devices we can design simplified circuits for computing carries – as shown in the next slide CSE 246 9

Improvement to Ripple Carry Adder: Manchester Adders CSE 246 10

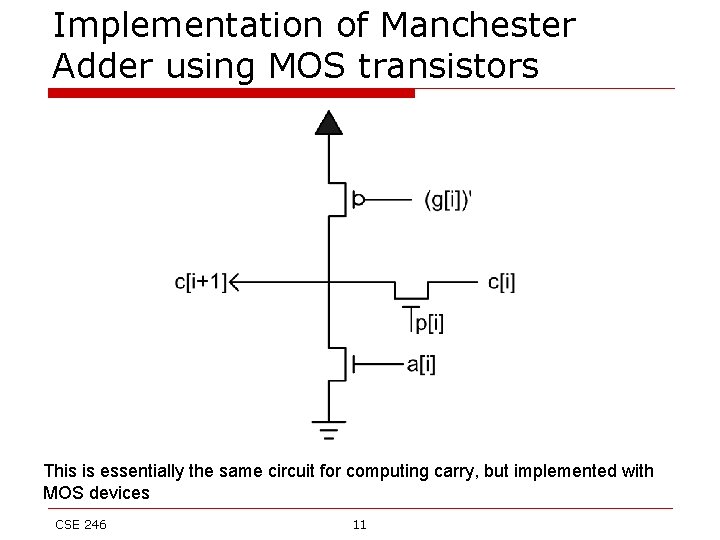
Implementation of Manchester Adder using MOS transistors This is essentially the same circuit for computing carry, but implemented with MOS devices CSE 246 11

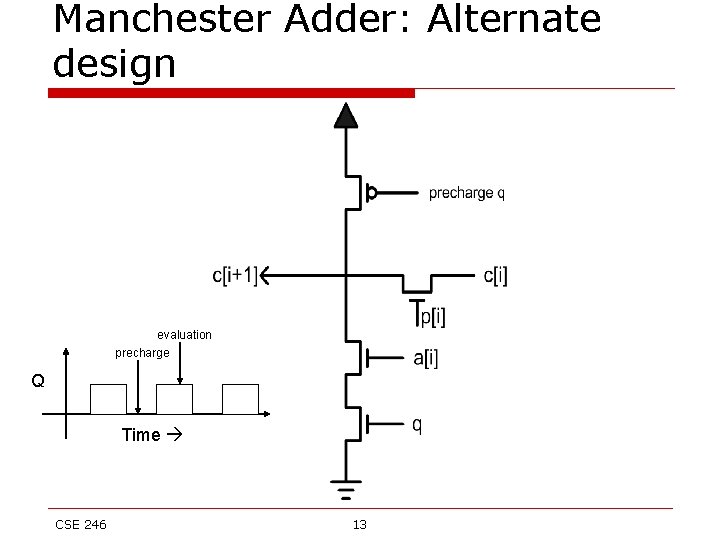
Manchester Adder: Alternate design o o We divide the computation cycle into two distinct half-cycle : ‘precharge’ and ‘evaluate’. In the precharge halfcycle, g[i] and c[i+1] are assigned a tentative value of logic 1. This is evaluated in the next half-cycle with actual value of a[i]. The actual circuit for computing carries is shown in the next slide. CSE 246 12

Manchester Adder: Alternate design evaluation precharge Q Time CSE 246 13

Carry Look-ahead Adder o o o In a ripple-carry adder m-full adders are grouped together (m is usually equal to 4). Once the carry-in to the group is known, all the internal carries and the output carry is calculated simultaneously. We can use some algebraic manipulations to minimize hardware complexity. Consider the carry out of the group n c[i] = g[i-1] + p[i-1]. c[i-1] n Putting the value of c[i-1], we can rewrite as c[i] = g[i-1] + p[i-1]. g[i-2] + p[i-1]. p[i-2]. c[i-2] n Proceeding in this manner we get c[i] = g[i-1] + p[i-1]. g[i-2] + p[i-1]. p[i-2]. g[i-3] + p[i-1]. p[i 2]. p[i-3]. g[i-4] + p[i-1]. p[i-2]. p[i-3]. p[i-4]. c[i-4] n To further simplify the equation, we note that g[i-1] = g[i-1]. p[i-1], and p[i-1] can be factored out CSE 246 14
![Lings Adder ci gi1 pi1 gi2 pi1 pi2 gi 3 Ling’s Adder c[i] = g[i-1] + p[i-1]. g[i-2] + p[i-1]. p[i-2]. g[i 3] +](https://slidetodoc.com/presentation_image_h2/9a1f40e2c09749b9d2bf077417c9e6fa/image-15.jpg)
Ling’s Adder c[i] = g[i-1] + p[i-1]. g[i-2] + p[i-1]. p[i-2]. g[i 3] + p[i-1]. p[i-2]. p[i-3]. g[i-4] + p[i-1]. p[i 2]. p[i-3]. p[i-4]. c[i-4] We replace p[i]=x[i]^y[i] with t[i]=x[i]+y[i]. Because g[i]=g[i]t[i], we have c[i] = g[i-1]t[i-1] + t[i-1]g[i-2] + t[i-1]. t[i 2]. g[i-3] + t[i-1]. t[i-2]. t[i-3]. g[i-4] + t[i 1]. t[i-2]. t[i-3]. t[i-4]. c[i-4] Let h[i] = g[i-1] + g[i-2] + t[i-2]. g[i-3] + t[i-2]. t[i -3]. g[i-4] + t[i-2]. t[i-3]. t[i-4]. t[i-5] h[i-4] C[i]= h[i]t[i-1] CSE 246 15
![Lings Adder h0c0 h3g2g1t1g0t1t0h0 s3p3c3p3h3t2 t3h3t2t3h3t2 h3p3h3p3t2 h6g5g4t4g3t4t3t2h3 s6h6p6h6p6t5 CSE 246 16 Ling’s Adder h[0]=c[0] h[3]=g[2]+g[1]+t[1]g[0]+t[1]t[0]h[0] s[3]=p[3]^c[3]=p[3]^(h[3]t[2]) =t[3]’h[3]t[2]+t[3](h[3]’+t[2]’) =h[3]’p[3]+h[3](p[3]^t[2]) h[6]=g[5]+g[4]+t[4]g[3]+t[4]t[3]t[2]h[3] s[6]=h[6]’p[6]+h[6]’(p[6]^t[5]) CSE 246 16](https://slidetodoc.com/presentation_image_h2/9a1f40e2c09749b9d2bf077417c9e6fa/image-16.jpg)
Ling’s Adder h[0]=c[0] h[3]=g[2]+g[1]+t[1]g[0]+t[1]t[0]h[0] s[3]=p[3]^c[3]=p[3]^(h[3]t[2]) =t[3]’h[3]t[2]+t[3](h[3]’+t[2]’) =h[3]’p[3]+h[3](p[3]^t[2]) h[6]=g[5]+g[4]+t[4]g[3]+t[4]t[3]t[2]h[3] s[6]=h[6]’p[6]+h[6]’(p[6]^t[5]) CSE 246 16

Generalized Design for Adders: Prefix Adder o Prefix computation Given n inputs x 1, x 2, x 3…xn and an associative operator ×. We want to compute yi = xi × xi-1 × xi-2 …× x 2 × x 1 for all i, 1≤ i ≤n n x can be a scalar/vector/matrix n For design of adders, we define the operator × in the following manner n o o o CSE 246 (g, p) = (g’, p’) × (g’’, p’’) g = g’’ + p’’. g’ p = p’. p’’ 17

Alternate modeling of Prefix Computer: Finite State Machine o A finite state machine has a set of states, and it ‘moves’ from one state to another according to input. Mathematically, n o o sk = f (sk-1, ak-1) The problem is to determine final state sn in O(lg n) operations, given initial state s 0 and sequence of inputs (a 0, a 1, …an-1) This problem can be formulated in terms of prefix computation CSE 246 18

Alternate modeling of Prefix Computer: Finite State Machine o o o We assume that number of states are small and finite. Let sk = fak-1(sk-1), fak-1 can be represented by matrix Mak-1 Now we are ready to represent our problem in terms of prefix computation. CSE 246 19

Alternate Modeling of Prefix Computer: Finite State Machine The algorithm Compute Mai in parallel Compute o 1. 2. N 1 = M a 1 N 2 = Ma 2. Ma 1 … Nn = Man-1…Ma 1 n n 3. Compute Si+1= Ni(S 0) CSE 246 20

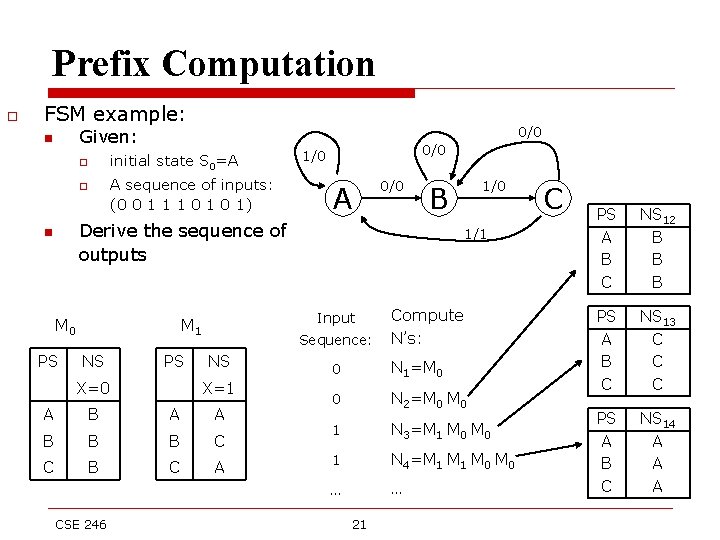
Prefix Computation o FSM example: n o o n 0/0 Given: initial state S 0=A A sequence of inputs: (0 0 1 1 1 0 1) 0/0 1/0 A 0/0 B Derive the sequence of outputs PSPS NS Next X=0 X=0 A A B B B C C B CSE 246 1/1 Input M 0 State table M 1 Sequence: PS State. NS X=1 X=1 AA A B BC C B CA A 1/0 Compute N’s: 0 N 1=M 0 0 N 2=M 0 1 N 3=M 1 M 0 1 N 4=M 1 M 0 … … 21 C PS A B C NS 12 B B B PS A B C NS 13 C C C PS A B C NS 14 A A A

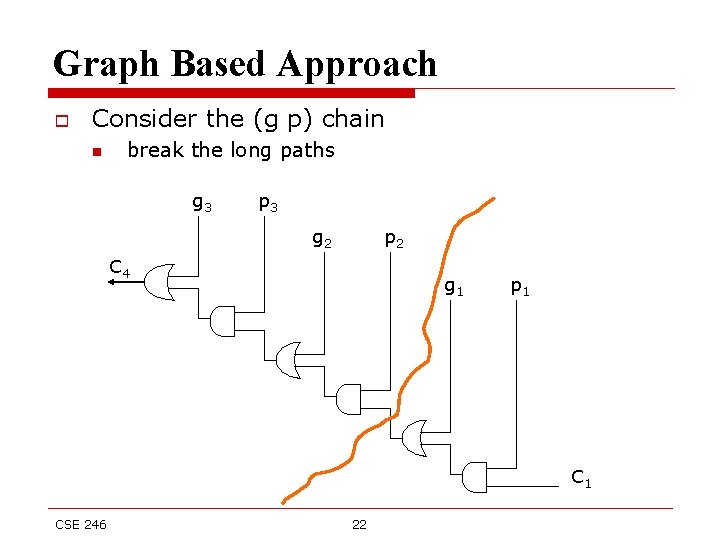
Graph Based Approach o Consider the (g p) chain n break the long paths g 3 p 3 g 2 p 2 C 4 g 1 p 1 CSE 246 22

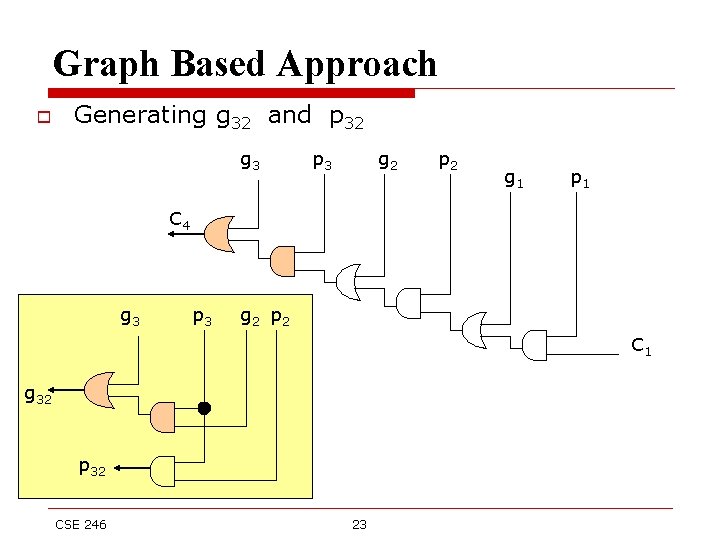
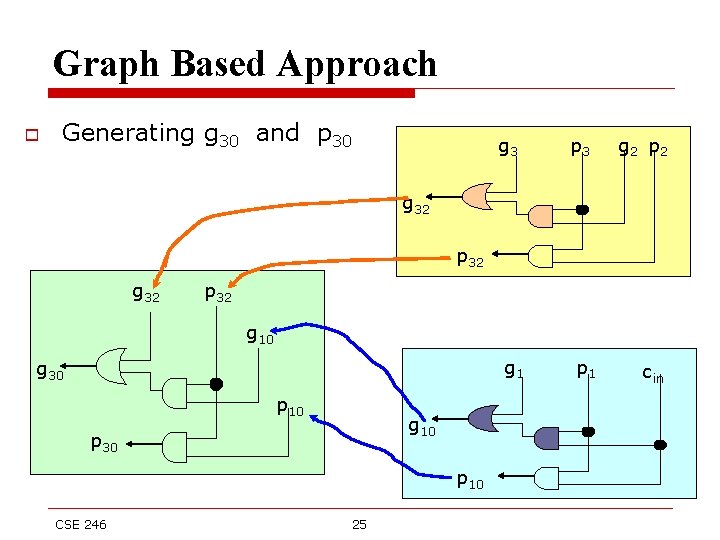
Graph Based Approach o Generating g 32 and p 32 g 3 p 3 g 2 p 2 g 1 p 1 C 4 g 3 p 3 g 2 p 2 C 1 g 32 p 32 CSE 246 23

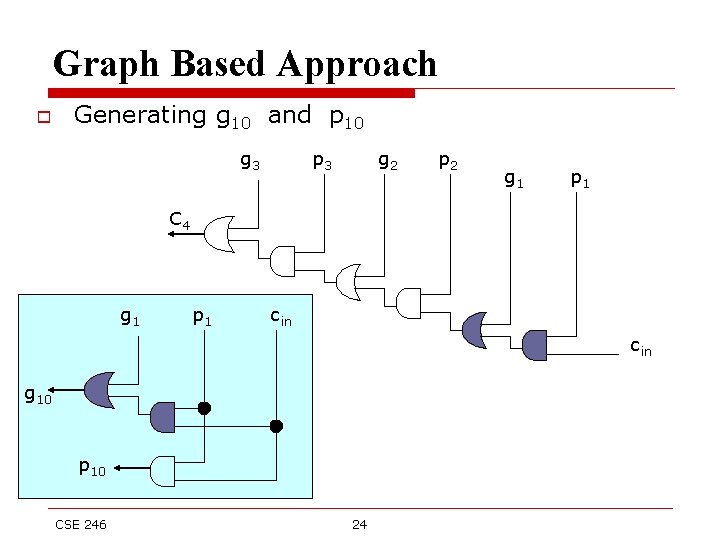
Graph Based Approach o Generating g 10 and p 10 g 3 p 3 g 2 p 2 g 1 p 1 C 4 g 1 p 1 cin g 10 p 10 CSE 246 24

Graph Based Approach o Generating g 30 and p 30 g 3 p 3 g 2 p 2 g 32 p 32 g 10 g 1 g 30 p 10 g 10 p 30 p 10 CSE 246 25 p 1 cin

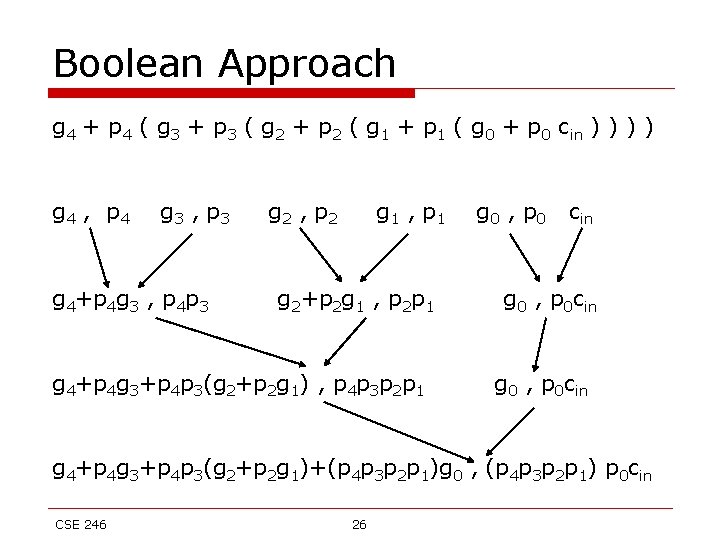
Boolean Approach g 4 + p 4 ( g 3 + p 3 ( g 2 + p 2 ( g 1 + p 1 ( g 0 + p 0 cin ) ) g 4 , p 4 g 3 , p 3 g 4+p 4 g 3 , p 4 p 3 g 2 , p 2 g 1 , p 1 g 2+p 2 g 1 , p 2 p 1 g 4+p 4 g 3+p 4 p 3(g 2+p 2 g 1) , p 4 p 3 p 2 p 1 g 0 , p 0 cin g 0 , p 0 cin g 4+p 4 g 3+p 4 p 3(g 2+p 2 g 1)+(p 4 p 3 p 2 p 1)g 0 , (p 4 p 3 p 2 p 1) p 0 cin CSE 246 26

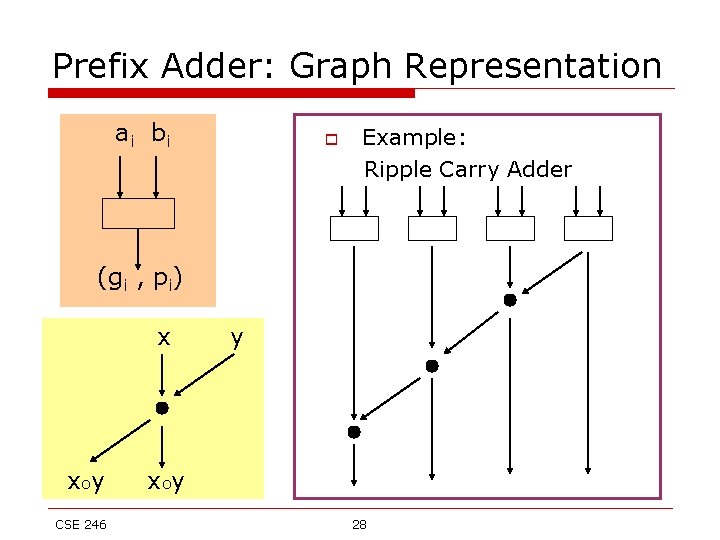
Prefix Adder o Given: n n o o n inputs (gi, pi) An operation o Associativity n (A o B) o C = A o ( B o C) Compute: n yi= (gi, pi) o … o (g 1, p 1) ( 1 <= i <= n) a, i=1 o o o (g’’, p’’) o (g’, p’) = (g, p) g=g’’ + p’’g’ p=p’’p’ CSE 246 27 gi = aibi , otherwise 1, i=1 pi = ai xor bi , otherwise

Prefix Adder: Graph Representation ai b i o Example: Ripple Carry Adder (gi , pi) x xoy CSE 246 y x oy 28

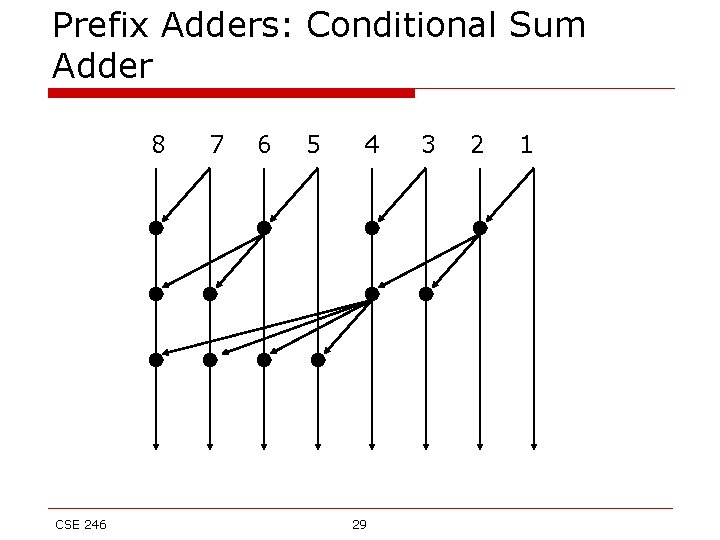
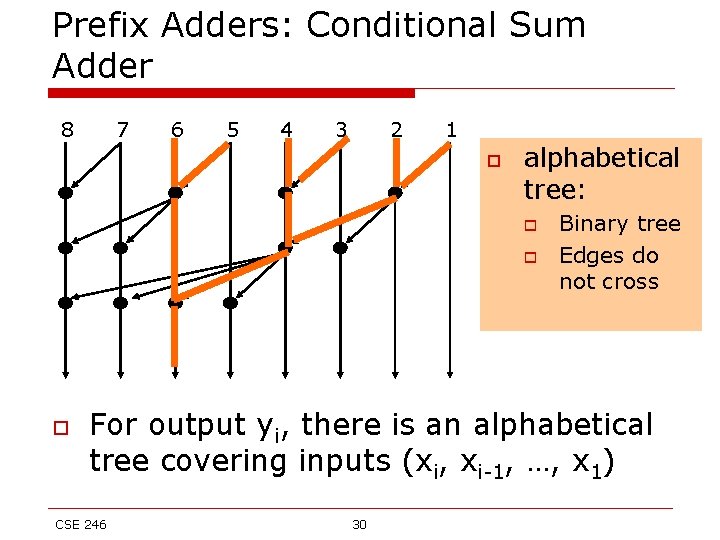
Prefix Adders: Conditional Sum Adder 8 CSE 246 7 6 5 4 29 3 2 1

Prefix Adders: Conditional Sum Adder 8 7 6 5 4 3 2 1 o alphabetical tree: o o o Binary tree Edges do not cross For output yi, there is an alphabetical tree covering inputs (xi, xi-1, …, x 1) CSE 246 30

Prefix Adders: Conditional Sum Adder 8 7 6 5 4 3 2 1 The nodes in this tree can be reduced to (g, p) o c = g+pc o o From input x 1, there is a tree covering all outputs (yi, yi-1, …, y 1) CSE 246 31

Prefix Adders: size and depth o Objective: n n o Ripple Carry Adder: n n n o Minimize # of nodes, sc(n). Minimize depth, dc(n) sc(8) = 7 dc(8) = 7 total = 14 Conditional Sum Adder: n n n CSE 246 sc(8) = 12 dc(8) = 3 total = 15 32

Prefix Adder – Well-known and Well-developed? o Classic prefix networks: Sklansky, Kogge. Stone, Brent-Kung, Ladner-Fischer, Han. Carlson, Knowles etc. CSE 246 33

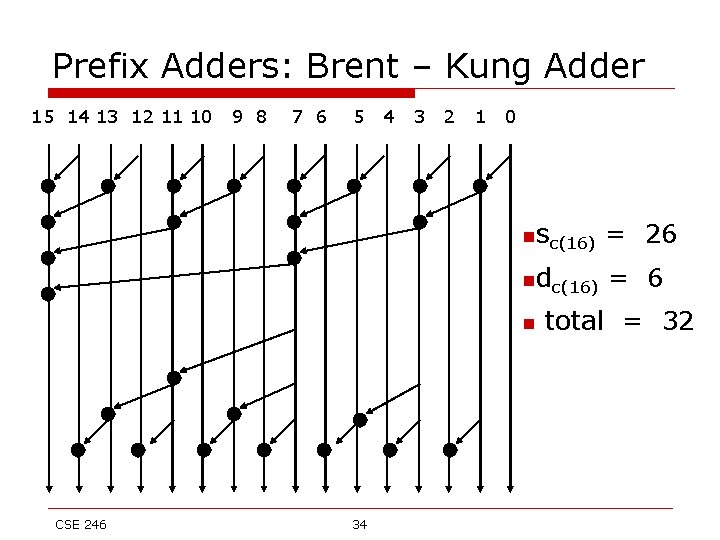
Prefix Adders: Brent – Kung Adder 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 nsc(16) = 26 ndc(16) = 6 n CSE 246 34 total = 32

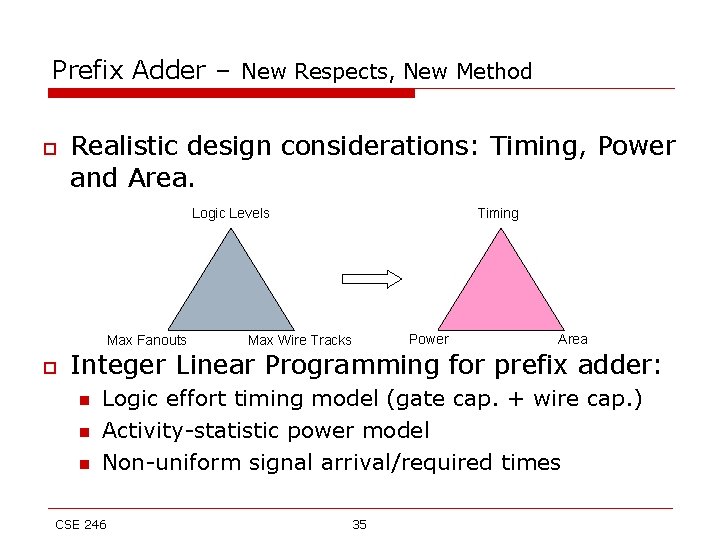
Prefix Adder – New Respects, New Method o Realistic design considerations: Timing, Power and Area. Logic Levels Max Fanouts o Timing Max Wire Tracks Power Area Integer Linear Programming for prefix adder: n n n Logic effort timing model (gate cap. + wire cap. ) Activity-statistic power model Non-uniform signal arrival/required times CSE 246 35

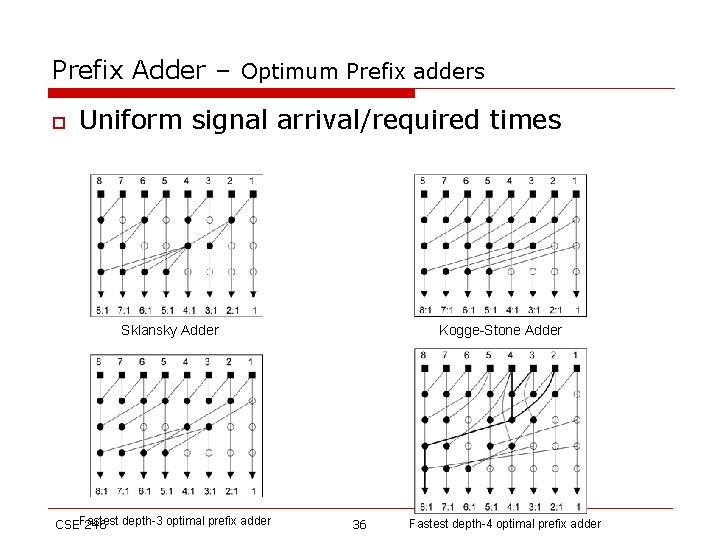
Prefix Adder – Optimum Prefix adders o Uniform signal arrival/required times Sklansky Adder CSEFastest 246 depth-3 optimal prefix adder Kogge-Stone Adder 36 Fastest depth-4 optimal prefix adder

Prefix Adder – Optimum Prefix adders o Uniform signal arrival/required times CSE 246 37

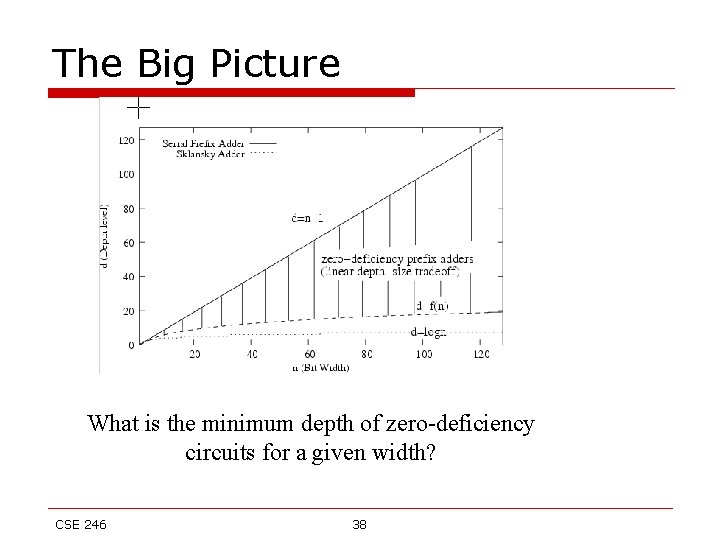
The Big Picture What is the minimum depth of zero-deficiency circuits for a given width? CSE 246 38

Proof for Snir’s Theorem Given an arbitrary prefix graph of width n, we have depth + size ≥ 2 n – 2 o Proof n n Consider the alphabetical tree rooted at the MSB output with all the input nodes being its leaves; The size of this tree is n-1 while its depth is d. M; At most d. M prefix outputs can be generated from this tree; At least one extra node is needed for the columns where the prefix results are not ready. Consequently size ≥ (n-1)+(n-(d. M + 1)) = 2 n -2 - d. M which is size + depth ≥ 2 n - 2 CSE 246 39

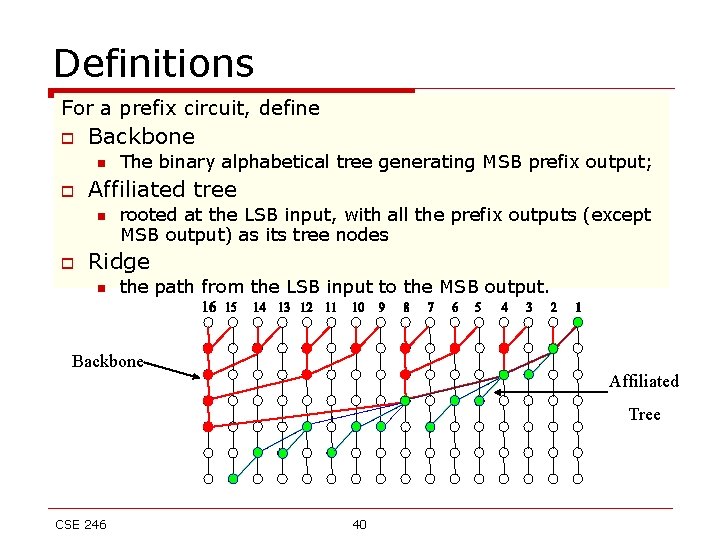
Definitions For a prefix circuit, define o Backbone n o Affiliated tree n o The binary alphabetical tree generating MSB prefix output; rooted at the LSB input, with all the prefix outputs (except MSB output) as its tree nodes Ridge n the path from the LSB input to the MSB output. Backbone Affiliated Tree CSE 246 40

How to … ? o o o Look from the MSB output Since the circuit is of zero-deficiency, the ridge has exactly d nodes (excluding the first input node), one node per level. The idea: try to stretch the ridge as long as possible while maintaining zerodeficiency CSE 246 41

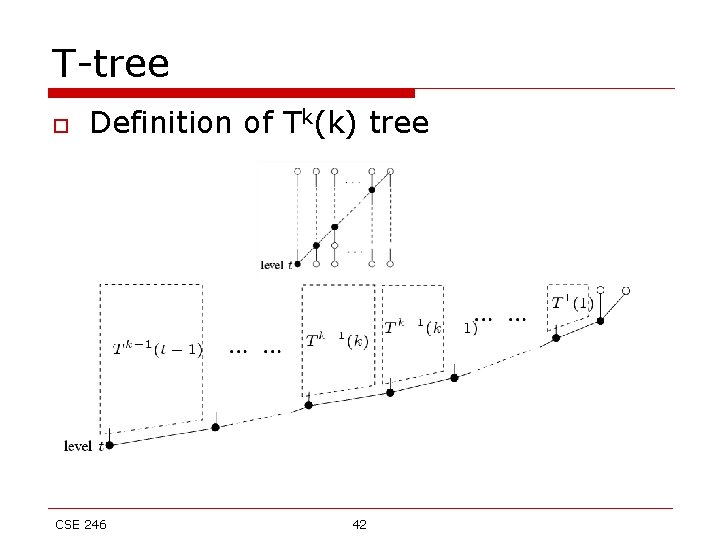
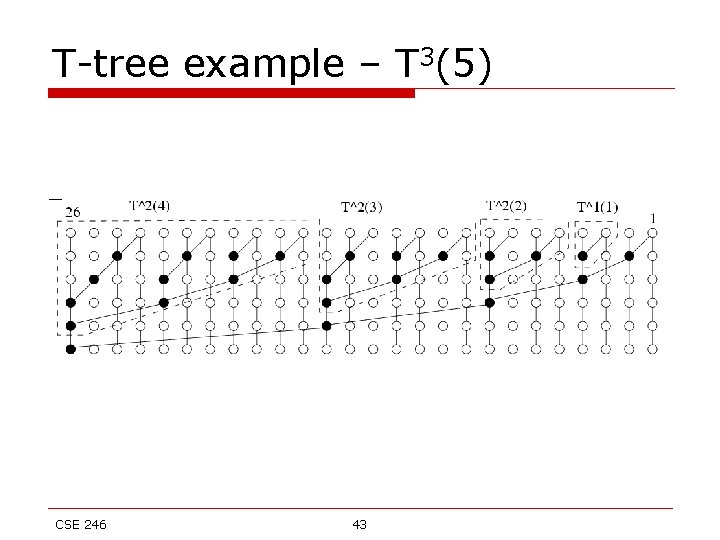
T-tree o Definition of Tk(k) tree CSE 246 42

T-tree example – T 3(5) CSE 246 43

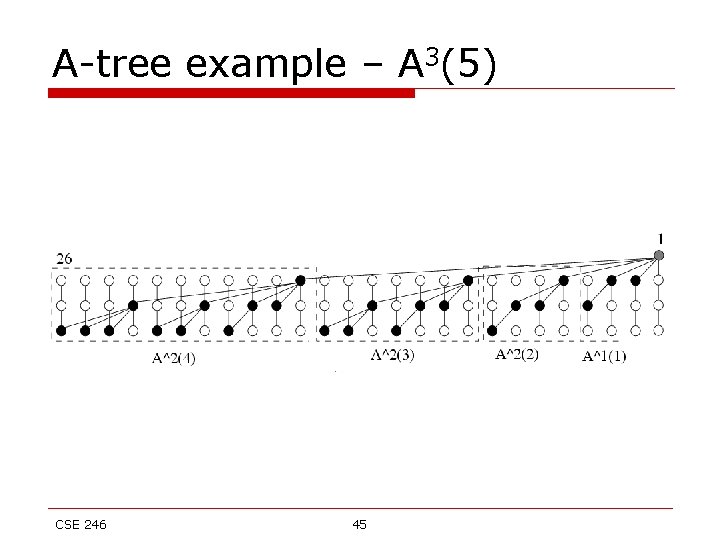
A-tree o Definition of Ak(t) tree CSE 246 44

A-tree example – A 3(5) CSE 246 45

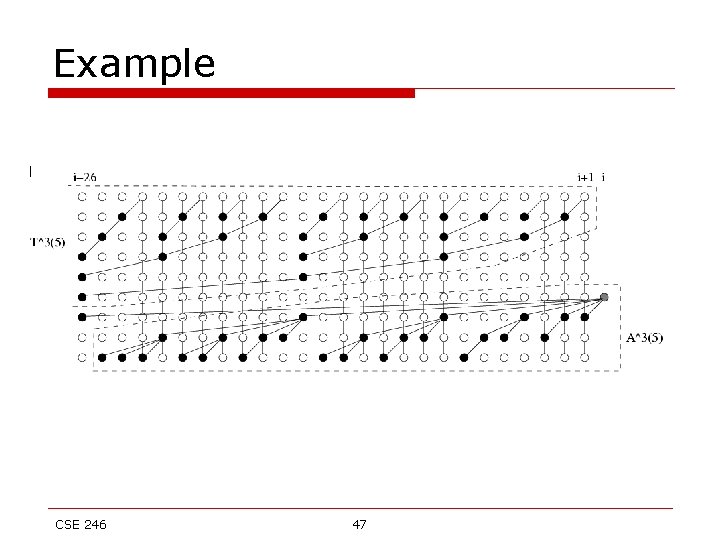
Compound of A tree and T-tree CSE 246 46

Example CSE 246 47

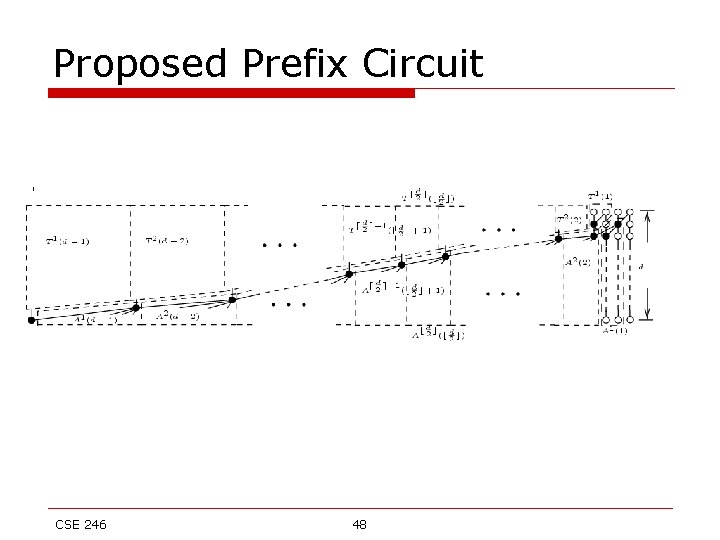
Proposed Prefix Circuit CSE 246 48

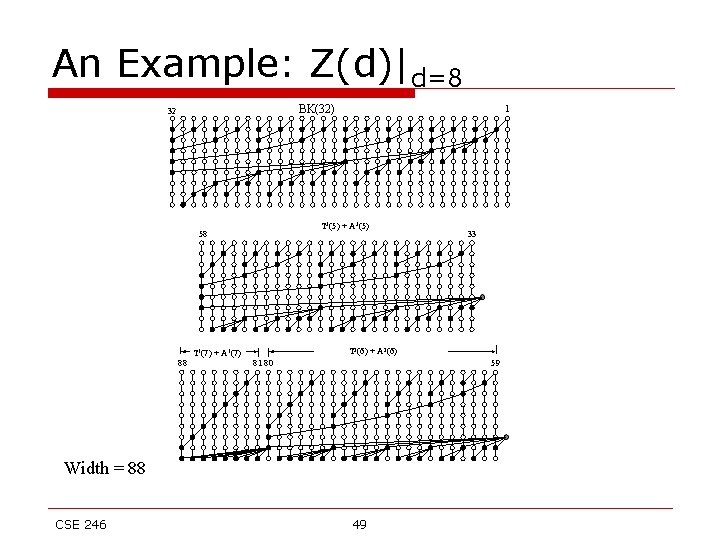
An Example: Z(d)|d=8 BK(32) 32 T 3(5) + A 3(5) 58 T 1(7) + A 1(7) 88 1 T 2(6) + A 2(6) 81 80 59 Width = 88 CSE 246 33 49

The width of Z(d) Circuit The width of Z(d) circuit is Nz(d) = F(d+3) – 1 (d≥ 1) Where F(i) are the Fibonacci numbers o Numerical Comparison o d LS LYD Z 3 7 7 7 D LS LYD 8 47 77 Z 88 D 13 4 5 6 7 9 10 11 12 143 232 376 609 14 383 15 517 16 575 17 1030 11 16 23 33 12 20 33 54 66 95 95 131 169 191 242 LS LYD Z D LS LYD Z 260 308 986 18 1535 1625 10945 446 576 843 1101 1596 2583 4180 6764 19 20 21 22 2055 3071 4104 6143 2139 3176 4202 6264 17710 28656 46367 75024 LYD : Design by S. Lakshmivarahan, C. M. Yang & S. K. Dhall, 1987 LS : Design by Lin & Shish, 1999 CSE 246 50

Comparison o o o 64 -bit case Based on logical effort method to include fan-out effect and interconnect capacitance Five adders n n n CSE 246 Z 64: A 64 -bit Z(d) circuit derived from Z(d)|d=8 BK: Brent-Kung adder Sklansky KS: Kogge-Stone adder HC: Han-Carlson Adder 51

Results o o w is the weight for lateral interconnect capacitance; KS and HC have large w value to compensate for coupling effect Z 64 and BK adder have similar delay and area, but Z 64 could be more power efficient because it has less logic levels CSE 246 52

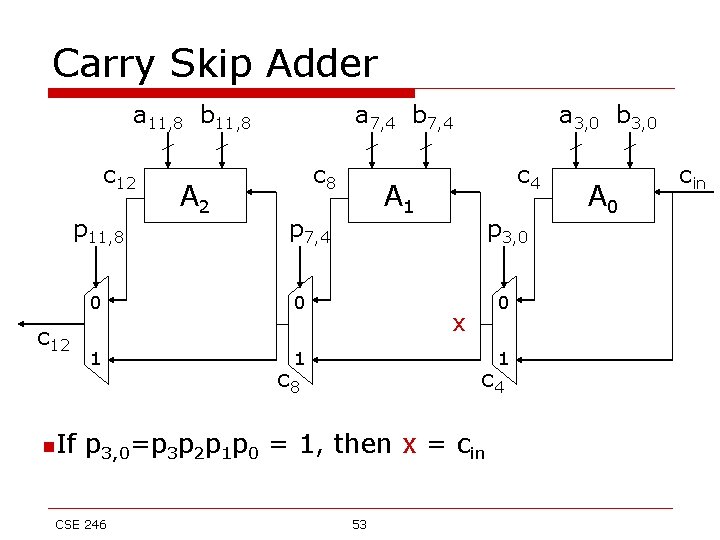
Carry Skip Adder a 11, 8 b 11, 8 c 12 p 11, 8 c 12 n. If A 2 a 7, 4 b 7, 4 c 8 0 1 1 c 4 A 1 p 7, 4 0 a 3, 0 b 3, 0 p 3, 0 0 x 1 c 8 c 4 p 3, 0=p 3 p 2 p 1 p 0 = 1, then x = cin CSE 246 53 A 0 cin

Carry Propagation Paths o o o o A 2 <- MUX <- cin A 2 <- MUX <- A 1 A 2 <- MUX <- A 0 c 12 <- MUX <- A 2 c 12 <- MUX <- A 1 c 12 <- MUX <- A 0 c 12 <- MUX <- cin CSE 246 54

False Path o A 1 <- MUX <- A 0 <- cin is a false path n n CSE 246 If carry is from cin, then block must have p 3 p 2 p 1 p 0 = 1 Since p 3, 0 = 1, g 3, 0 must be 0 The carry is not generated from A 0 The carry needs not to propagate via A 0, it will go from the MUX 55

Label Algorithm o Problem: n n o Given a digraph, a set of false paths Derive the longest path of the graph Algorithm: n n n CSE 246 Color the edges on each false path a label The length of the walk of the same labels are accumulated Otherwise, change to no label 56
 Fftooo
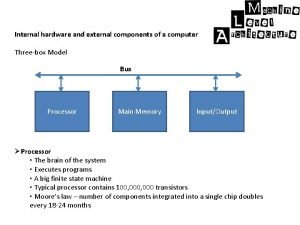
Fftooo Internal and external components of computer
Internal and external components of computer En un zoológico hay 246 aves
En un zoológico hay 246 aves It 246
It 246 Afman 10-246
Afman 10-246 Mining of massive datasets stanford
Mining of massive datasets stanford Write the highlighted digits place and value 567
Write the highlighted digits place and value 567 Cs 246
Cs 246 Hyperglycemie nhg
Hyperglycemie nhg Psalm 246
Psalm 246 15 diezmilésimos en decimales
15 diezmilésimos en decimales Cs 246
Cs 246 Round 215 to the nearest hundred
Round 215 to the nearest hundred Mining massive datasets
Mining massive datasets Design and analysis of algorithms syllabus
Design and analysis of algorithms syllabus Introduction of design and analysis of algorithms
Introduction of design and analysis of algorithms Binary search in design and analysis of algorithms
Binary search in design and analysis of algorithms Introduction to the design and analysis of algorithms
Introduction to the design and analysis of algorithms Design and analysis of algorithms
Design and analysis of algorithms Design and analysis of algorithms
Design and analysis of algorithms Comp 482
Comp 482 Data representation and computer arithmetic
Data representation and computer arithmetic Routing algorithms in computer networks
Routing algorithms in computer networks Drawing algorithms
Drawing algorithms Computer hardware & network maintenance
Computer hardware & network maintenance Hardware and software in computer graphics
Hardware and software in computer graphics Introduction to computer hardware
Introduction to computer hardware Four major data processing functions of a computer
Four major data processing functions of a computer Design techniques of algorithms
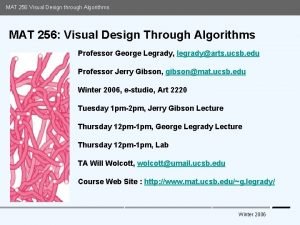
Design techniques of algorithms Algorithms for visual design
Algorithms for visual design Mat256
Mat256 Computer arithmetic
Computer arithmetic Behrooz parhami computer arithmetic
Behrooz parhami computer arithmetic Fixed point addition and subtraction flowchart
Fixed point addition and subtraction flowchart Square root algorithm
Square root algorithm Computer organization and architecture william stallings
Computer organization and architecture william stallings Computer arithmetic
Computer arithmetic Flowchart for memory reference instructions
Flowchart for memory reference instructions Cse 598 advanced software analysis and design
Cse 598 advanced software analysis and design Hardware acquisition in system analysis and design
Hardware acquisition in system analysis and design Language tool
Language tool Computer hardware platforms in it infrastructure
Computer hardware platforms in it infrastructure Computer hardware platforms in it infrastructure
Computer hardware platforms in it infrastructure Computer hardware 101
Computer hardware 101 Computer hardware classification
Computer hardware classification Computer hardware platforms in it infrastructure
Computer hardware platforms in it infrastructure Graphic organizer of computer hardware
Graphic organizer of computer hardware Hardware gcse computer science
Hardware gcse computer science Major hardware components
Major hardware components Computer hardware servicing nc2
Computer hardware servicing nc2 Access memory
Access memory First generation of computer
First generation of computer Software brings the machine to life
Software brings the machine to life Mengidentifikasi berbagai komponen perangkat keras komputer
Mengidentifikasi berbagai komponen perangkat keras komputer Computer hardware slides
Computer hardware slides Computer graphics introduction ppt
Computer graphics introduction ppt Hardware topic
Hardware topic