CSE 246 Computer Arithmetic Algorithms and Hardware Design

CSE 246: Computer Arithmetic Algorithms and Hardware Design Fall 2006 Lecture 2: Redundant and residue number systems Instructor: Prof. Chung-Kuan Cheng CSE 246

Topics: o o Redundant Number Systems Residue Number Systems n CSE 246 Mixed Radix Number Systems (as they pertain to conversions of Residue Number Systems) 2

Redundant Number Systems o Examine number systems that can be characterized by the 3 -tuple (r, , ) n o r : radix, [ , ] : set of digits The redundancy of such a system is said to be n non-redundant if - + 1 = r n redundant if - + 1 > r o o o CSE 246 minimally redundant if - = r maximally redundant if - =2 r - 1 over redundant if - > 2 r - 1 3

Redundant Number Systems o Ex: (2, 0, 2) n Redundant - furthermore, minimally redundant Addition example: 1 +1 2 + 2 0 1 1 1 2 CSE 246 2 (6) 1 (7) 3 [3 not in radix] 1 1 = 4*2 + 2*2 +1 = 13 = 6+7 4 4 2 1 0 0 0 0 0 1 1 1 2 2 2 0 0 1 2 0 0 1 2 2 3 4 4 5 6 4

Redundant Number Systems o More addition examples: 110 +102 212 CSE 246 121 +101 222 101121 +112210 111 11 11 21 222211 111222 +112222 20 20 20 11 22 11220 11 2 1121220 5

Redundant Number Systems o What has redundancy bought us? n n CSE 246 From the examples, it seems carry propagation has been somewhat reduced Intuitively - redundancy acts as a buffer against carry propagation However, carry propagation was not eliminated in (2, 0, 2) Need to formalize the degree to which a particular degree of redundancy eliminates carry propagation 6

Redundant Number Systems o To formalize: xi+1 xi + yi+1 yi ti+1 wi ti+2 wi+1 where xi + yi = r*ti+1 + wi+1 we must bound ti+1 + wi+1 for all i to eliminate carry propagation CSE 246 7

Redundant Number Systems As xi and yi are in [ , ] and xi + yi = r * ti+1 + wi+1 1 2 r*ti+1 + wi 2 suppose there exist and such that 2 ti+1 we need 3 - wi+1 - to avoid propagation. Since this must be true for all i, whether the subscript is i or i+1 is not important. From 2 & 3 we have 4 r* + - r*ti+1 + wi+1 r* + - From 1 & 4 we have 5 CSE 246 2 r* + - 8

Redundant Number Systems 2 r* + - gives the following bounds for & to insure no propagation 5 /(r-1) For (2, 0, 2): /(r-1) -> 2/(2 -1) /(r-1) -> 0/(2 -1) which, from 3 means all wi must be in the range [0, 0] and there exist inputs requiring carry propagation CSE 246 9

Redundant Number Systems o How then to ensure that no carry propagation is needed? n Change (r, , ) Consider (3, 0, 5) /(r-1) -> 5/(3 -1) /(r-1) -> 0/(3 -1) yields : 3 (first integer after 5/2) : 0 From 3, this gives a range on wi of [0, 2] Thus, when presented with multiple possibilities for representing the sum of two digits, always choose terms in [0, 2] and there will be no carry propagation CSE 246 10

Redundant Number Systems Ex: for (3, 0, 5) 243 +435 22 21 20 2232 CSE 246 5+3 = 8 could use 15, but choose from [0, 2] yielding 22 and no propagation 11

Redundant Number Systems o Advantages n o Constant time addition/subtraction! Disadvantages n n More space Comparison o o o no unique forms/representations conversion to canonical form as expensive as summation Uses: n excellent for intermediate results of addition o o CSE 246 Multiplication DSP loops that have no comparisons 12

Residue Number Systems o Define a Residue Number System as follows For any given integer x, x=(x 1|x 2|. . . |xk)RNS(P 1|P 2|. . . |Pk) where xi = x mod Pi and i, j Pi is relatively prime to Pj EX: 84 = (0|4|0)RNS(7|5|3) 1 = (1|1|1)RNS(7|5|3) 2 = (2|2|2)RNS(7|5|3) 3 = (3|3|0)RNS(7|5|3) Residue numbers are not positional. Residue numbers have unique representations mod i. e. for (7|5|3) there are unique representations of 0 -104. CSE 246 13

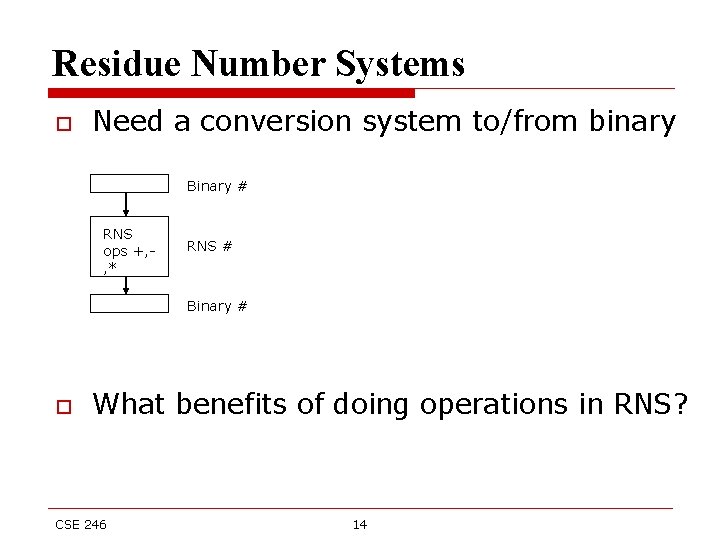
Residue Number Systems o Need a conversion system to/from binary Binary # RNS ops +, , * RNS # Binary # o What benefits of doing operations in RNS? CSE 246 14

Residue Number Systems o Addition (subtraction is similar) x+y = ((x 1+y 1)p | (x 2+y 2)p |. . . | (xk+yk)p )RNS(P 1|P 2|. . . |Pk) where xi = (x)p and yi = (y)p 1 2 i o k i Multiplication x*y = ((x 1*y 1)p | (x 2*y 2)p |. . . | (xk*yk)p )RNS(P 1|P 2|. . . |Pk) where xi = (x)p and yi = (y)p 1 i o 2 k i Division ? n CSE 246 Hard. What does a fraction look like in RNS? 15

Residue Number Systems o Advantages: n n o Disadvantages: n n n o Parallel processing of +, *, - on smaller numbers Adding more primes without increasing range allows for use of fields to assist in fault tolerance (Ex: go from (7|5|3) to (7|5|3|2) where last field is used for parity) No division Comparison non-trivial Conversion costs How to do conversion? CSE 246 16

Residue Number Systems o Conversion: RNS -> Binary # Given (x 1|x 2|. . . |xk)RNS(P 1|P 2|. . |Pk) Binary number x = where i = inv mod See: Chinese Remainder Theorem One may consider, for the purposes of computation, all i as being a pre-defined part of each particular RNS system CSE 246 17

Residue Number Systems o Conversion -> Bin# example: 84 = (0|4|0)RNS(7|5|3) For (7|5|3): ( 1* 5*3)7 = 1 1 : 1 ( 2* 7*3)5 = 1 2 : 1 ( 3* 7*5)3 = 1 3 : 2 x = (0* 1*5*3*7/7 + 4* 2*7*3*5/5 + 0* 3*7*5*3/3)105 x = (0 + 4* 2*21 + 0)105 x = (4*1*21)105 = 84105 CSE 246 18

Residue Number Systems o Conversion -> Bin # example: 1 = (1|1|1)RNS(7|5|3) ( 1* 5*3)7 = 1 1 : 1 ( 2* 7*3)5 = 1 2 : 1 ( 3* 7*5)3 = 1 3 : 2 x = (1* 1*5*3*7/7 + 1* 2*7*3*5/5 + 1* 3*7*5*3/3)105 x = (1* 1*15 + 1* 2*21 + 1* 3*35)105 x = (1*1*15+1*1*21+1*2*35)105=(106)105 = 1105 CSE 246 19

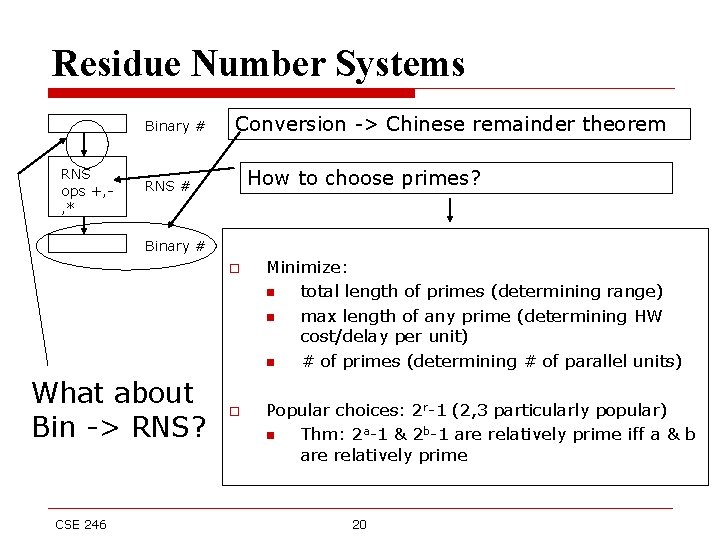
Residue Number Systems Binary # RNS ops +, , * Conversion -> Chinese remainder theorem How to choose primes? RNS # Binary # o What about Bin -> RNS? CSE 246 o Minimize: n total length of primes (determining range) n max length of any prime (determining HW cost/delay per unit) n # of primes (determining # of parallel units) Popular choices: 2 r-1 (2, 3 particularly popular) n Thm: 2 a-1 & 2 b-1 are relatively prime iff a & b are relatively prime 20

Residue Number Systems o Binary # to RNS conversion n Uses a lookup table Observation: for n digit binary number y (yn-1, yn-2, . . . , y 0)p = [(2 n-1)p *yn-1+ (2 n-2)p *yn-2+. . . +(20)p *y 0]p i Use a table to store (2 i)p i i Example for (7|5|3) (1011)=(x 1|x 2|x 3)RNS(7|5|3) x 1 = (1+2+1)7 = 4 x 2 = (3+2+1)5 = 1 x 3 = (2+2+1)3 = 2 CSE 246 21 i i i

Residue Number Systems o Comparison n n CSE 246 Could convert back and forth to/from binary. Another approach: convert to a mixed radix system, as numbers in a mixed radix system are comparable. 22

Mixed Radix Number Systems o We shall describe a Mixed Radix System as follows: x =(Zk-1|Zk-2|. . . Z 0)MRS(Pk-1|Pk-2|. . . |P 1) x = Zk-1 Pk-2. . . P 1 + Zk-2 Pk-1. . . P 0 +. . . + Z 1 P 1+Z 0 CSE 246 23

Mixed Radix Number Systems o Conversion from RNS to MRS Given x = (xk-1|xk-2|. . . |x 0)RNS(Pk-1|Pk-2|. . . |P 0) We want x=(Zk-1|Zk-2|. . . |Z 0)MRS(Pk-2|Pk-3|. . . |P 0) Observation: The MRS digit Z 0 is in units of 1, so fewer primes needed in MRS than in RNS CSE 246 24

Mixed Radix Number Systems o Question: what is the relationship between x 0 and Z 0? n n Can it be found by simple inspection? Yes. 1 x 0 = Z 0. n n CSE 246 Why? x 0 is the residue left from x mod P 0 - all other terms are multiples of P 0 -> x 0 = Z 0 25

Mixed Radix Number Systems o This yields 2 x-x 0 = (x’k-1|x’k-2|. . . |x’ 1|-)RNS(Pk-1|Pk-2|. . . |P 1|-) = (Zk-1|Zk-2|. . . |Z 1|0)MRS(Pk-2|Pk-3|. . . |P 0) where x’i = (xi-x 0)p i Note that this is the only change in MRS CSE 246 26

Mixed Radix Number Systems o 3 Which leads to (x-x 0)/P 0 = (x”k-1|x”k-2|. . . |x” 1|-)RNS(Pk-1|Pk-2|. . . |P 1|-) = (Zk-1|Zk-2|. . . |Z 1) MRS (Pk-2|Pk-1|. . . |P 1) Z 1 = x” 1 and so forth. (Deduction, division, repeat) However, it was earlier noted that division in RNS is hard - yet here we are doing division. The trick? In this case, we know that we will always get integer results. CSE 246 27

Back to RNS o Division in RNS x”i =xi * (P 0 -1)p i where (Pj-1)p is the multiplicative inverse of Pj with respect to Pi i Ex: CSE 246 (3 -1)7 = 5 --> (3*(3 -1)7)7 = 1 (3 -1)5 = 2 --> (3*(3 -1)5)5 = 1 28

Example: RNS -> MRS Y=(1|3|2)RNS(7|5|3) = (Z 2|Z 1|Z 0)MRS(5|3) That is, Y = Z 2*5*3+Z 1*3+Z 0 by 1 (see slide #25) Z 0 = x 0 = 2 from 2 (see slide #26) we have y-x 0 = y-2 =(x’ 2|x’ 1|0)RNS(7|5|3) = (Z 2|Z 1|0)MRS(5|3) x’ 2 = (x 2 -x 0)p = (1 -2)7 = 6 x’ 1 = (3 -2)5 = 1 y-2 = (6|1|0)RNS(7|5|3)=(Z 2|Z 1|0)MRS(5|3) 2 CSE 246 29

Example continued. 3 (See slide #27) then gives (y-x 0)/P 0= (y-2)/3 = (x” 2|x” 1|-)RNS(7|5|3) = (Z 2|Z 1)MRS(5) then Q: How does one derive x” 2 ? A: “It’s hard. ” One has to try values one by one up to the modulus remembering that (3 -1)7 = 5, (3 -1)5 = 2 x” 2= (5*6)7 = 2, x” 1 =(1*2)5 = 2 (y-2)/3 = (2|2|-)RNS(7|5|3) = (Z 2|Z 1)MRS(5) CSE 246 30

Ex. Cont. Apply 1 again, Z 1=x” 1=2 gives by 2 (y-x 0)/P 0 - x” 1 = (x”’ 2|0|-)RNS(7|5|3) = (Z 2|0)MRS(5) x”’ 2 =(x” 2 -2)7 = (2 -2)7 = 0 (0|0|-)RNS(7|5|3)=(Z 0|0)MRS(5) By 3 x”” 2 = (x”’ 2*(5 -1)7)7 = 0 = Z 2 Yields final result (0|2|2)MRS(5|3) CSE 246 31

Ex. Concluded. Check correctness (0|2|2)MRS(5|3) = 0*5*3+2 = 8 87 = 1, 85 = 3, 83 = 2 -> (1|3|2)RNS(7|5|3) Correct! o Closing remark / Moral of the examples “Inversion is key” CSE 246 32