Computer Systems Data Representation and Computer Arithmetic Data







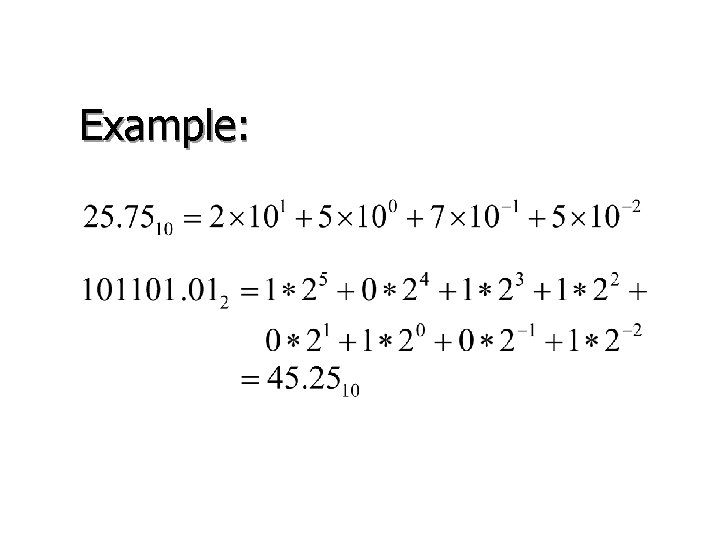

























- Slides: 39

Computer Systems Data Representation and Computer Arithmetic

Data Representation • Binary codes used to represent numbers • Conversion between number systems – Binary decimal – Hexadecimal – Between arbitrary number systems • Representation of positive/negative numbers • Floating point representation

Bit, Byte and Word • Bit is the smallest quantity that can be handled by computer: 1 or 0. • Byte is a group of 8 bits. • Word is the basic unit of data that can be operated by computer: e. g. , 16 bits. 11001010 00001101 Byte Word Bit • Some architectures have 8, 32, or 64 -bit words

Content of Word • Bit Pattern • May represent many things • Actual meaning of a particular bit pattern is given by the programmer • Computer itself cannot determine the meaning of the word • Classic question: Can you tell the meaning of a word picked randomly from the memory?

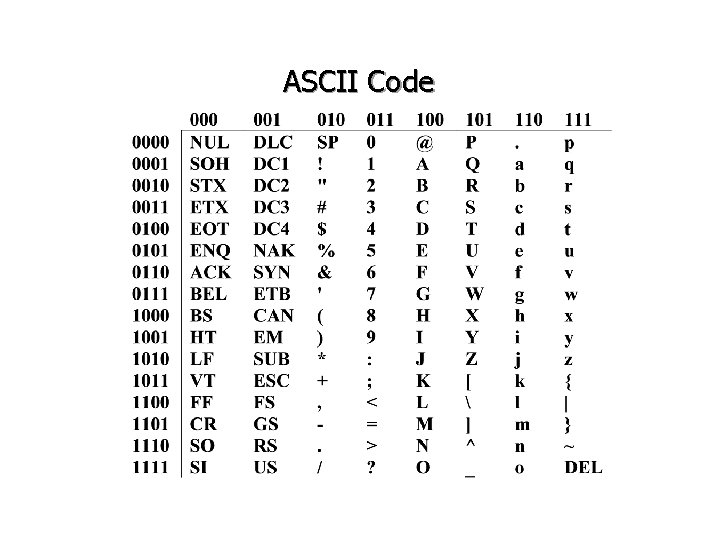
• Instruction: (op-code) A single word defines an action that is to be performed by CPU • Numeric Quantity • Character: A to Z, a to z, 0 to 9, *, -, +, etc. • ASCII Code: - Representation of a character by 7 bits. - The ASCII for W is 101 01112, or 5716

ASCII Code

Pixel (Picture Element) • • The smallest unit to construct a picture 1 bit/pixel for black-and-white pictures, >1 bits/pixel for gray scale or color pictures, e. g. 24 bits/pixel. • A letter is represented by a group of pixels on computer screen. Pixel (1)

Positional Notation • Weight is associated with the location within a number. • The 9 in 95 has weight 10 • A number N in base b is represented by
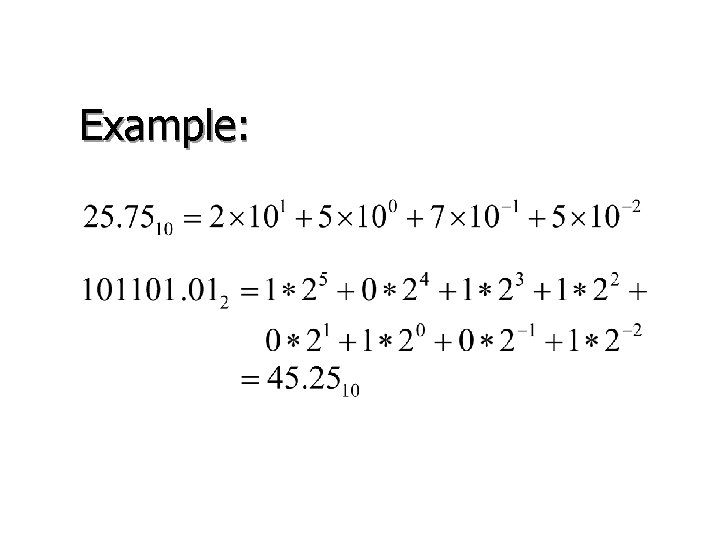
Example:

Number Bases • Decimal (b=10): {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} • Binary (b=2): {0, 1} • Octal (b=8): {0, 1, 2, 3, 4, 5, 6, 7} • Hexadecimal (b=16): {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F}

How many binary bits are needed to represent an n-digits decimal? The value of an m-bit binary is up to The value of an n-digit decimal is up to so OR

Questions How many bits are needed to represent an n-digits octal? How many bits are needed to represent an n-digits hexadecimal?

Conversion of Integer - Decimal to Binary • Divide a decimal successively by 2, record the remainder, until the result of the division is 0. 67/2 = 33 33/2 = 16 16/2 = 8 8/2 = 4 Rem. =1 Rem. =0 4/2 2/2 1/2 =2 =1 =0 Rem. =1

Conversion of Integer - Decimal to Hexadecimal • Divide a decimal successively by 16, record the remainder, until the result is 0 432/16 = 27 27/16 = 1 1/16 =0 Rem. =B Rem. =1

Conversion of integer - Binary to Decimal Conversion of integer - Hexadecimal to Decimal

Conversion of integer - Hexadecimal 01010111 5 2 Binary B 7 0010 1011 0111 7 Conversion of integer: - Octal Binary 01010111 1 2 7 2 5 7 010 101 111

Conversion of Fraction - Decimal to Binary • The fraction is repeatedly multiplied by 2, the integer part is stripped and recorded. 0. 687510 = 0. 10112 0. 687510 * 2 =1. 375 0. 37510 * 2 = 0. 7510 * 2 = 1. 5 0. 510 * 2 = 1. 0 0. 010 * 2 = 0. 0 1 1 end Question: Convert 0. 625? 0. 110?

Conversion of Fraction - Binary Hexadecimal 0. 1010110012 = 0. 1010 1100 10002 = 0. AC 816 0. 7 BC 16 = 0. 0111 1011 11002 = 0. 011112 Convert 0. 6 D 5? Convert 0. 1100101011

Binary Coded Decimal (BCD) • A decimal digit is coded into 4 bits 1 byte can store 2 digits Decimal 0 • Example: 1 2 1942 is encoded as 3 0001 1001 0100 0010 (2 bytes) 4 5 • Disadvantages • Complex arithmetic • Inefficient use of storage • Advantage: • Can represent “real” number 6 7 8 9 BCD 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001

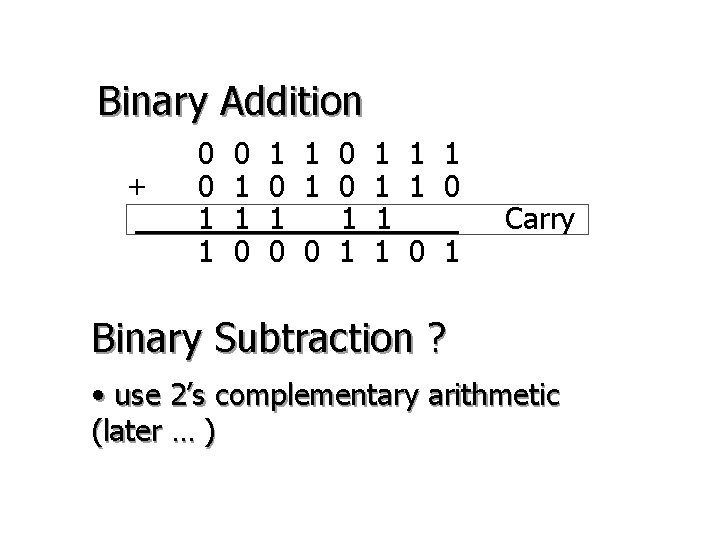
Binary Addition + 0 0 1 1 0 1 1 1 0 0 1 1 0 1 Carry Binary Subtraction ? • use 2’s complementary arithmetic (later … )

Signed Integer Representations • Sign-and-Magnitude • 1’s Complement • 2’s Complement

Sign-and-Magnitude Representation • Use the most significant bit (MSB) to indicate the sign of the number. • The MSB is 0 for positive, 1 for negative. • 8 bits represent -12710 to 12710 • Examples: 00101100 for +44 10101100 for -44 10 10 Problem: 0000 = +0, 10000000 = -0

1’s Complement • Just flip the bits! • The MSB is 0 for positive, 1 for negative. • 8 bits represent -12710 to 12710 • Examples: 00101100 for +44 11010011 for -44 10 10 Problem: 0000 = +0, 1111 = -0

2’s Complement • The 2’s complement for N is • Example: Using 5 bits (n = 5), if N = 7, then 01100 12 + 11001 -7 1) 0 0 1 5 • 2’s complement = 1’s complement + 1 7 00111 1’s complement 11000 + 1 2’s complement 1 1 0 0 1 = -7

2’s Complement (con. ) • To form the two’s complement of a number, simply invert the bits (1 to 0, 0 to 1), and add 1 1’s complement + 1 1310 = 0 0 1 1 0 1 -1310 = 1 1 0 0 1 0 + 1 =1111 0011 2’s comp. -34?

Properties of 2’s Complement • One unique 0 • MSB = 0, positive number • MSB = 1, negative number • The range is • For 5 bits, the range is -1610 (10000) to +1510 (01111) • The 2’s complement of the complement of X is X itself (Prove: )

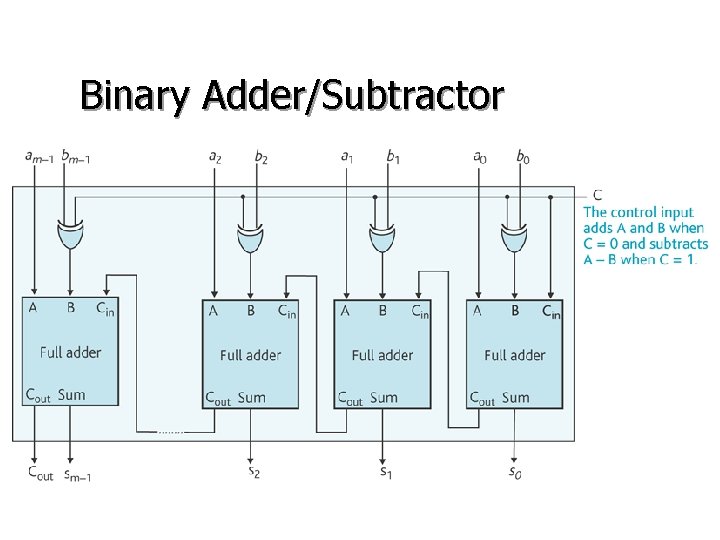
2’s Complementary Arithmetic • Subtraction is performed using addition A - B = A + (-B) X = 910 = 010012, -X = -910 = 101112, Y = 610 = 001102 -Y = -610 = 110102 X -Y 3 - X - Y -15 10 01001 + 11010 1) 0 0 0 1 1 10 10111 + 11010 1) 1 0 0 0 1

Binary Adder/Subtractor

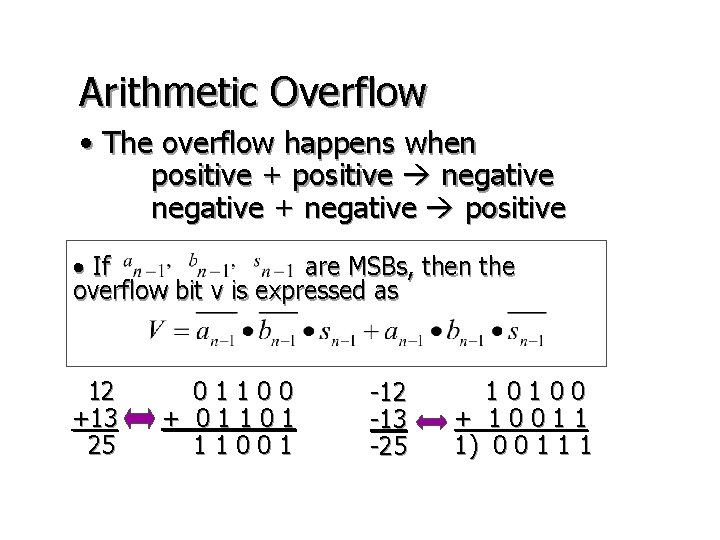
Arithmetic Overflow • The overflow happens when positive + positive negative + negative positive • If are MSBs, then the overflow bit v is expressed as 12 +13 25 01100 + 01101 11001 -12 -13 -25 10100 + 10011 1) 0 0 1 1 1

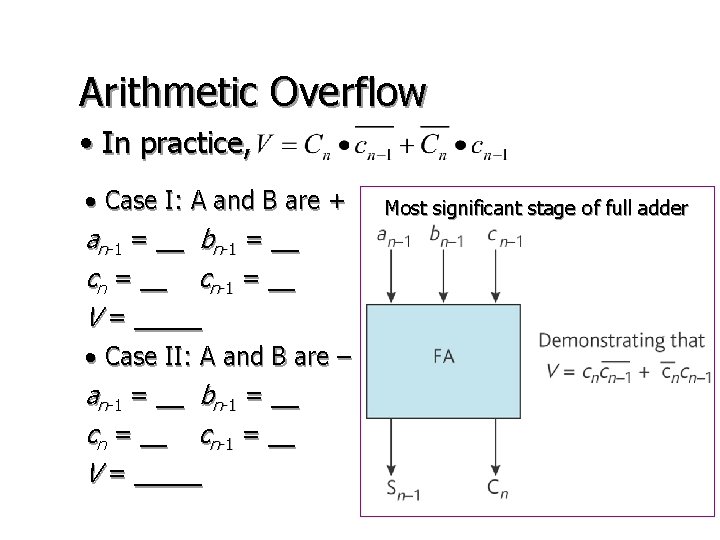
Arithmetic Overflow • In practice, • Case I: A and B are + an-1 = __ bn-1 = __ cn-1 = __ V = _____ • Case II: A and B are – an-1 = __ bn-1 = __ cn-1 = __ V = _____ Most significant stage of full adder

Fixed-point Arithmetic 3. 62510 0011. 10102 + 6. 510 0110. 10002 + 10. 12510 00111010 0110100010 The fraction point is added 10100010 -> 1010. 00102 What if we want to represent ? We need at least m > 3. 3*n = 3. 3*20 = 66 bits !

Floating Point Numbers • Scientific Notation a is mantissa, r is radix, e is exponent • is for binary

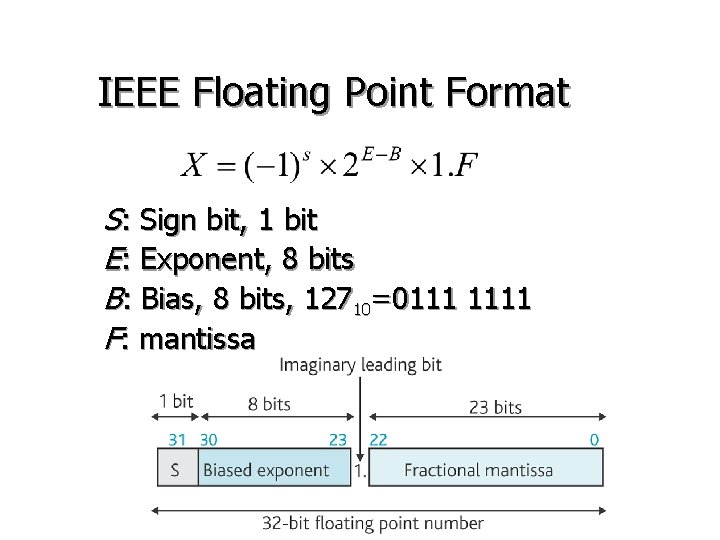
IEEE Floating Point Format S: Sign bit, 1 bit E: Exponent, 8 bits B: Bias, 8 bits, 12710=0111 1111 F: mantissa

IEEE Floating Point - Example • Normalization, e. g. , • Use sign and magnitude representation for signed mantissa. • Use biased exponent, e. g. in excess 127 • If we have 8 bits for exponent, to represent -5, we add 12710 (0111 1111) to -5, the result is 12210=0111 10102.

IEEE Floating Point - Example Represent -2345. 125 in 32 bits ? -2345. 125 = -1001001. 0012 1) Normalization: 2) Negative mantissa, so S = 1 3) Exponent: E = 11 + 127 = 13810 = 100010102 4) Mantissa F = 001001 0010… 000 1 10001010 001001001000… 0 1. 510 in IEEE format?

IEEE Floating Point Format – Special Cases • Zero: exponent and fraction all 0 s • Denormalized: exponent all 0 s, fraction non-zero for single precision: • Infinity: exponents all 1 s, fraction all 0 s sign bit determines +infinity or -infinity • Not a Number (Na. N): exponents all 1 s, fraction non-zero • A good reference is available at http: //research. microsoft. com/~hollasch/cgindex/coding/ieeefloat. html

Bit Patterns and Logical Operations • AND • OR • NOT • Exclusive OR They are bit-wise operations.

AND Operation • x AND y is true, if and only if both bits x and y are true. A=11001011 B=01101101 C=A AND B =01001001 OR Operation • x OR y is true, if either bits x or y is true. C=A OR B A=11001011 B=01101101 =11101111

NOT Operation • A 1 becomes 0, and a 0 becomes 1. A=11001011 C = NOT A = 0 0 1 1 0 0 EOR (Exclusive OR) Operation • It is true, if and only if just one of inputs is true. A=11001011 B=01101101 C = A EOR B = 1 0 0 1 1 0