CSC 4170CSC 8510 Theory of Computation ContextFree Grammars

CSC 4170/CSC 8510 Theory of Computation Context-Free Grammars Chapter 2

2. 1. a What is a CFG Terminals: 0, 1 Variables: A, B Productions: Start variable: A Derivation: A B 0 A 1 0 B 1 00 A 11 0011 A B Parse tree: A B A B 0 A 1 0 A 1 B 0 A 1

2. 1. b Our grammar simplified A 0 A 1 A A 0 A 1 00 A 11 000 A 111 0000 A 1111 00001111 What language does this grammar produce?

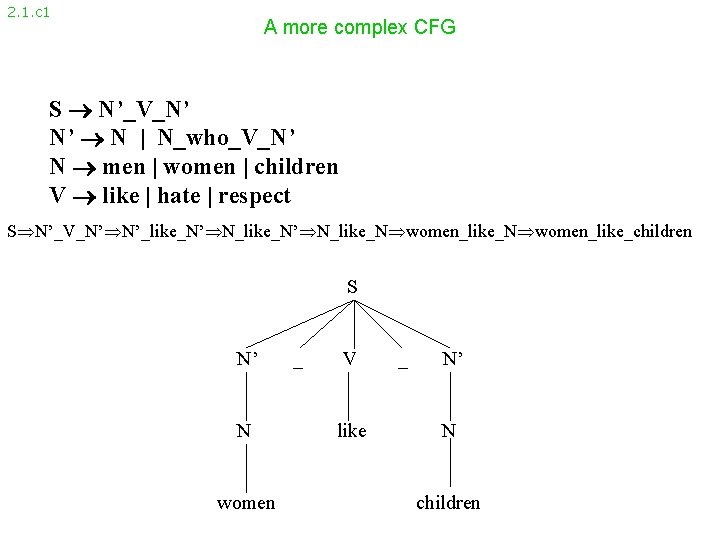
2. 1. c 1 A more complex CFG S N’_V_N’ N’ N | N_who_V_N’ N men | women | children V like | hate | respect S N’_V_N’ N’_like_N’ N_like_N women_like_children S N’ N women _ V like _ N’ N children

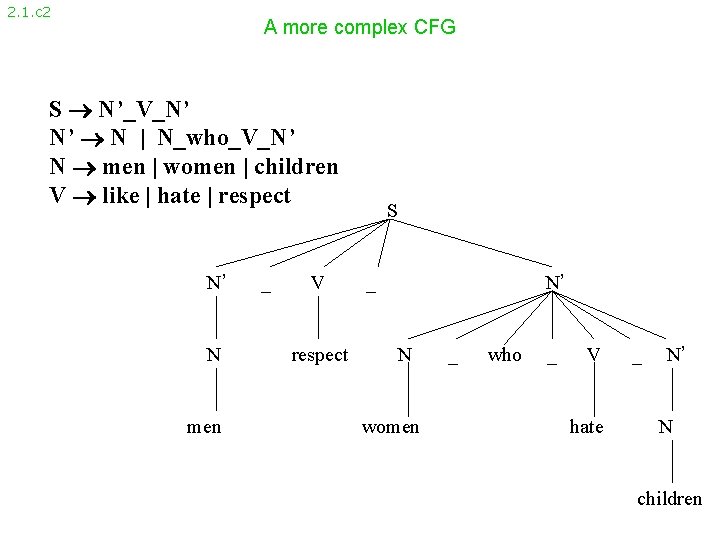
2. 1. c 2 A more complex CFG S N’_V_N’ N’ N | N_who_V_N’ N men | women | children V like | hate | respect N’ N men _ V respect S _ N’ N women _ who _ V hate _ N’ N children

2. 1. d Formal definitions A context-free grammar is a 4 -tuple (V, , R, S), where 1. V is a finite set called the variables; 2. is a finite set, disjoint from V, called the terminals; 3. R is a finite set of rules, with each rule being a pair of a variable and a string of variables and terminals; 4. S is an element of V called the start variable. If u, v, and w are strings of variables and terminals and A w is a rule, we say that u. Av yields uwv, written u. Av uwv. x * y means that x=y, or x y, or there are z 1, …, zn such that x z 1 … zn y. The language produced (defined, described) by the grammar is {w | S * w and w is a string of (only) terminals}. A context-free language is a language produced by some CFG.

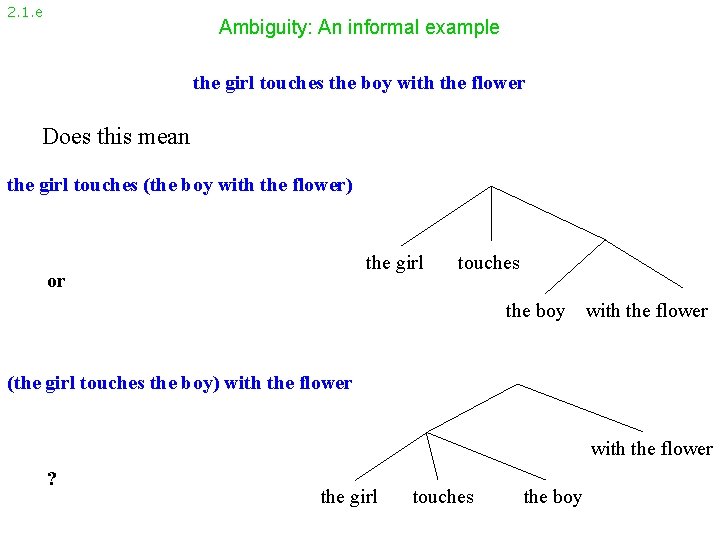
2. 1. e Ambiguity: An informal example the girl touches the boy with the flower Does this mean the girl touches (the boy with the flower) the girl or touches the boy with the flower (the girl touches the boy) with the flower ? the girl touches the boy

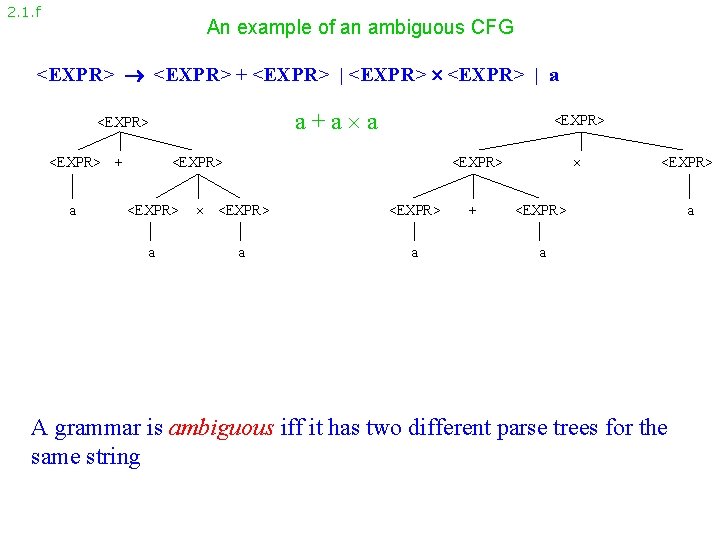
2. 1. f An example of an ambiguous CFG <EXPR> + <EXPR> | a a+a a <EXPR> + a <EXPR> <EXPR> a a + <EXPR> a A grammar is ambiguous iff it has two different parse trees for the same string a

2. 1. g An equivalent but unambiguous grammar <EXPR> + <TERM> | <TERM> a | a <EXPR> <TERM> a + <TERM> a a+a a a

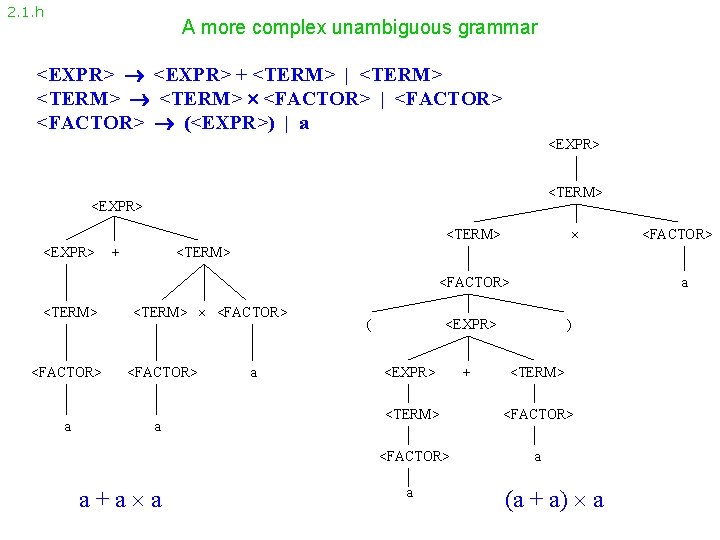
2. 1. h A more complex unambiguous grammar <EXPR> + <TERM> | <TERM> <FACTOR> | <FACTOR> (<EXPR>) | a <EXPR> <TERM> <EXPR> + <TERM> <FACTOR> a <FACTOR> <TERM> <FACTOR> a a+a a a ( a <EXPR> + ) <TERM> <FACTOR> a a (a + a) a

2. 1. i Designing context-free grammars Design a CFG that produces all regular expressions over the alphabet {0, 1}: <RE> Design a CFG G that produces the union of the languages produced by two given CFGs G 1 and G 2. G 1: A 1 w 1 … An wn G 2: B 1 u 1 … B m um

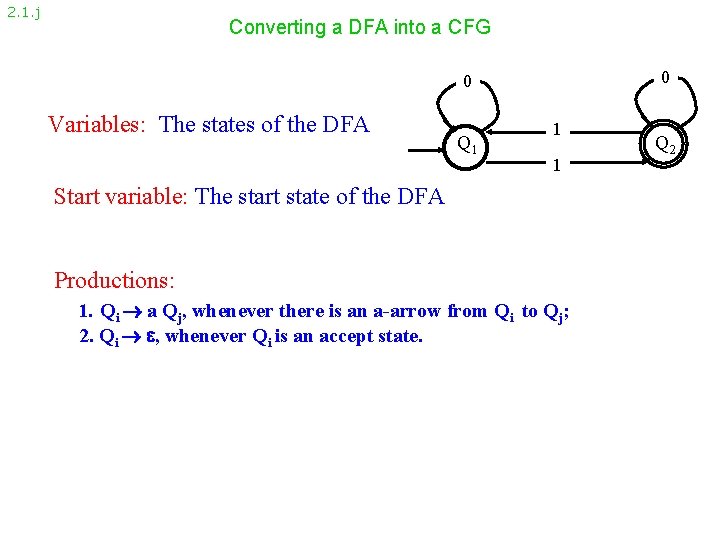
2. 1. j Converting a DFA into a CFG 0 0 Variables: The states of the DFA Q 1 1 1 Start variable: The start state of the DFA Productions: 1. Qi a Qj, whenever there is an a-arrow from Qi to Qj; 2. Qi , whenever Qi is an accept state. Q 2

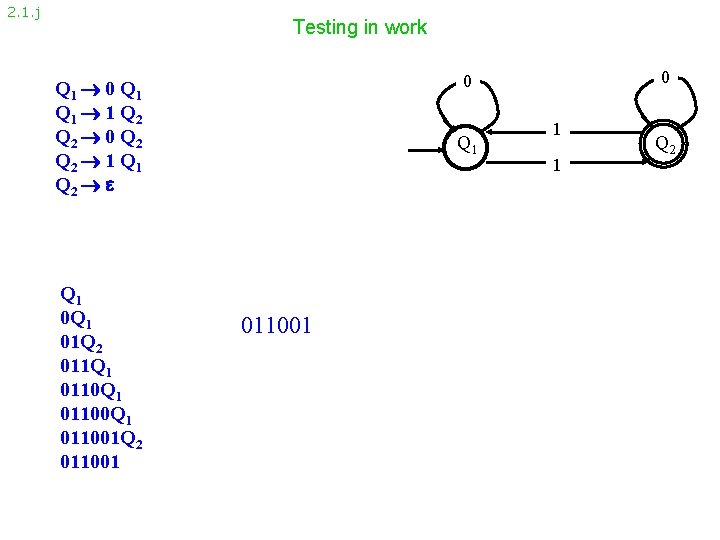
2. 1. j Testing in work Q 1 01 Q 2 011 Q 1 01100 Q 1 011001 Q 2 011001 0 0 Q 1 Q 1 1 Q 2 0 Q 2 1 Q 2 Q 1 011001 1 1 Q 2

2. 2 Giorgi Japaridze Theory of Computability Pushdown automata Just as to regular languages correspond finite automata, to context-free languages correspond pushdown automata. This is a new model of computation. What makes a PDA different from NFA is that it has potentially infinite, stack-type (LIFO) memory, where unlimited number of things can be remembered (pushed) and read (popped). A given transition depends on not only the current symbol in the input, but also the symbol currently at the top of the stack. PDAs are still not the most powerful machines. This is because of their limited (LIFO) access to memory.

2. 2. a Components of a pushdown automaton (PDA) x y x z Stack Input a a b a c … Push: write a symbol on the top of the stack Pop: delete a symbol from the top of the stack . . . (Q, , s, F) Q is the set of states is the input alphabet is the stack alphabet is the transition function s is the start state F Q is the set of accept states q 1 a, x y q 2 If the input symbol is a and the top stack symbol is x, go from q 1 to q 2, pop x and push y If a= , the read head is not advanced If x= , nothing is popped If y= , nothing is pushed

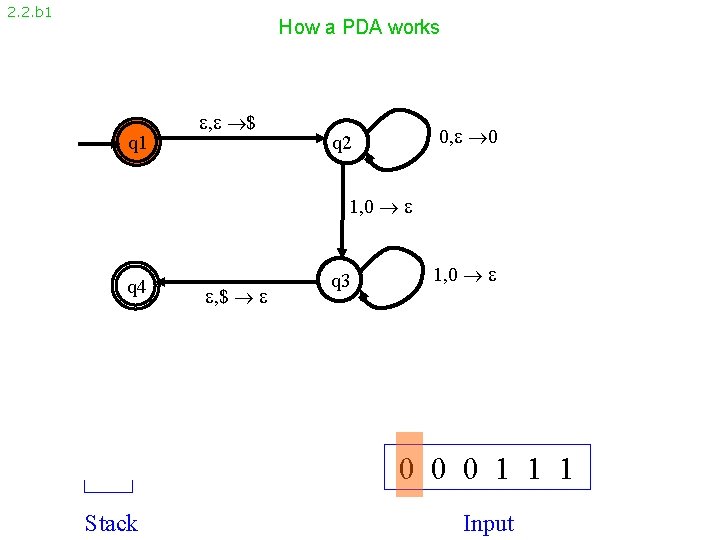
2. 2. b 1 How a PDA works q 1 , $ 0, 0 q 2 1, 0 q 4 , $ q 3 1, 0 0 1 1 1 Stack Input

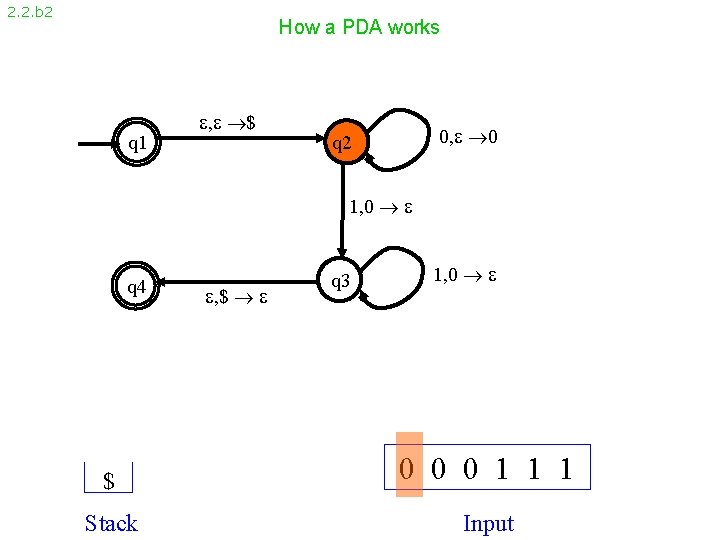
2. 2. b 2 How a PDA works q 1 , $ 0, 0 q 2 1, 0 q 4 , $ q 3 1, 0 $ 0 0 0 1 1 1 Stack Input

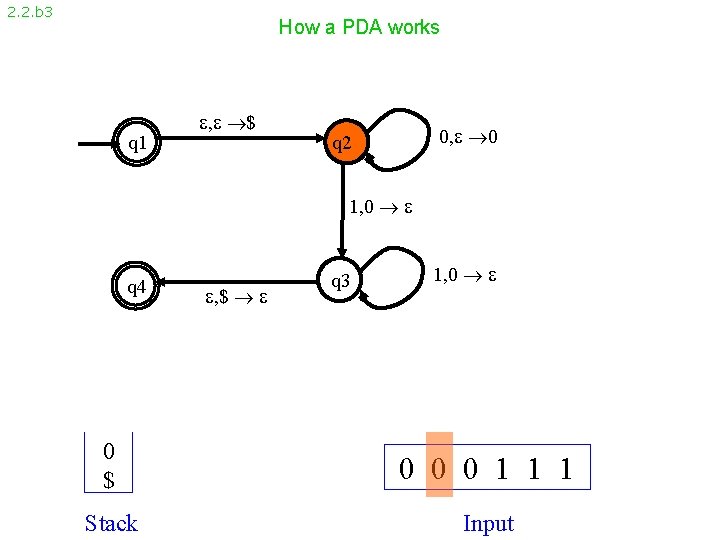
2. 2. b 3 How a PDA works q 1 , $ 0, 0 q 2 1, 0 q 4 , $ q 3 1, 0 0 $ 0 0 0 1 1 1 Stack Input

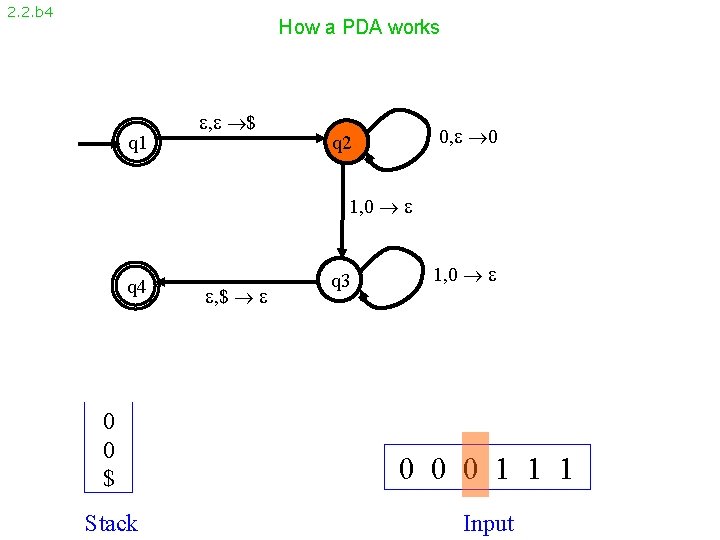
2. 2. b 4 How a PDA works q 1 , $ 0, 0 q 2 1, 0 q 4 , $ q 3 1, 0 0 0 $ 0 0 0 1 1 1 Stack Input

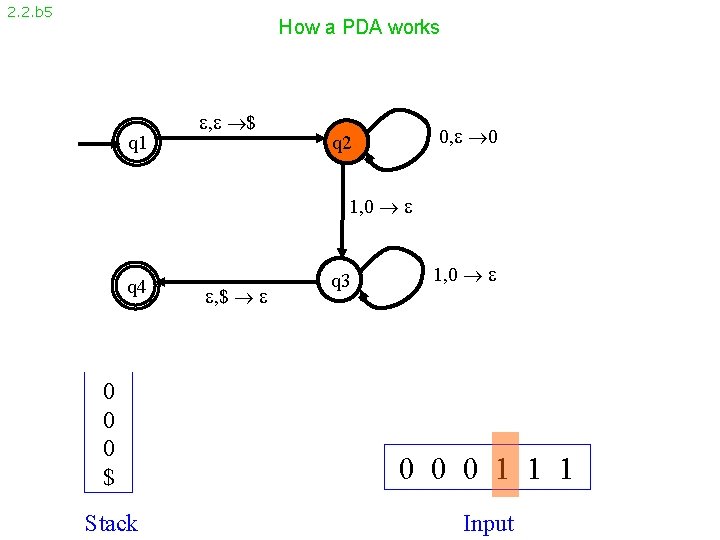
2. 2. b 5 How a PDA works q 1 , $ 0, 0 q 2 1, 0 q 4 , $ q 3 1, 0 0 $ 0 0 0 1 1 1 Stack Input

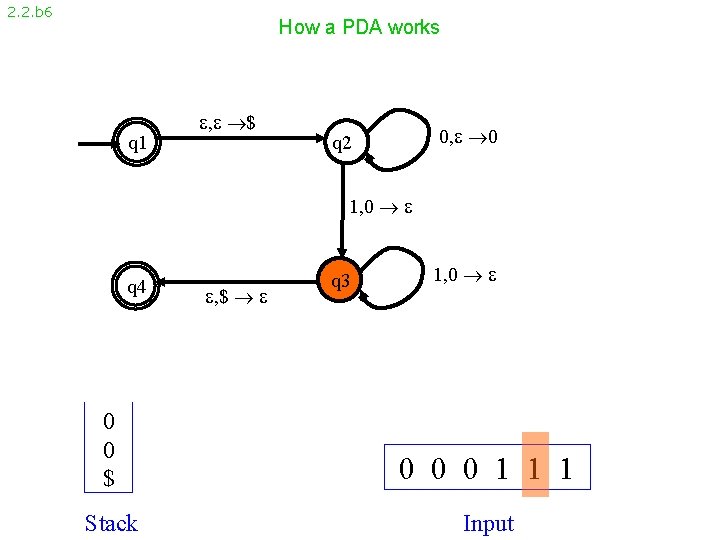
2. 2. b 6 How a PDA works q 1 , $ 0, 0 q 2 1, 0 q 4 , $ q 3 1, 0 0 0 $ 0 0 0 1 1 1 Stack Input

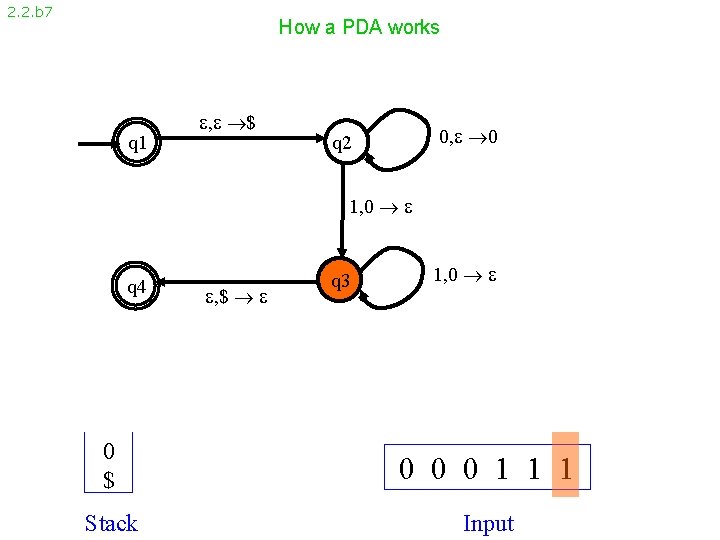
2. 2. b 7 How a PDA works q 1 , $ 0, 0 q 2 1, 0 q 4 , $ q 3 1, 0 0 $ 0 0 0 1 1 1 Stack Input

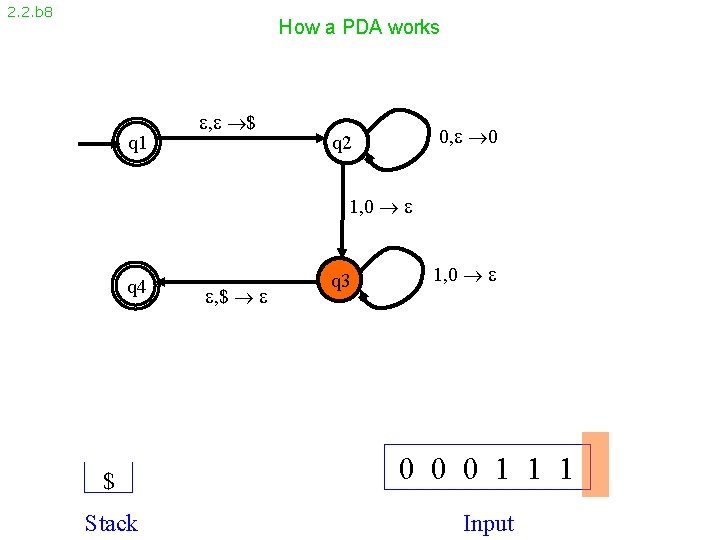
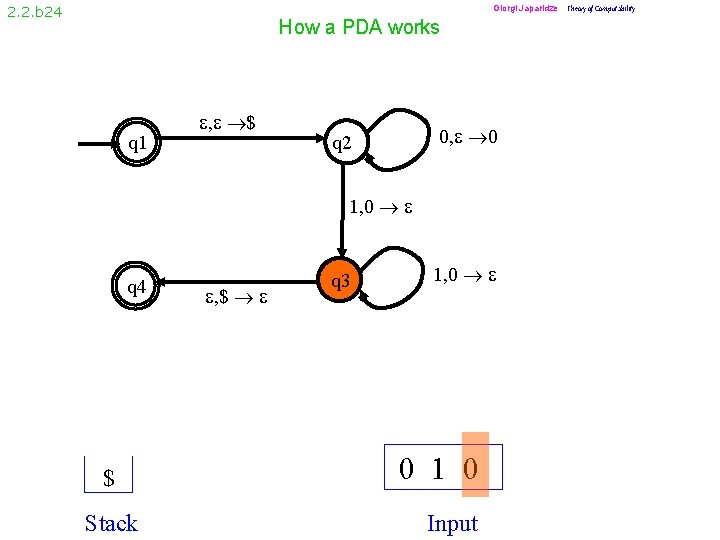
2. 2. b 8 How a PDA works q 1 , $ 0, 0 q 2 1, 0 q 4 , $ q 3 1, 0 $ 0 0 0 1 1 1 Stack Input

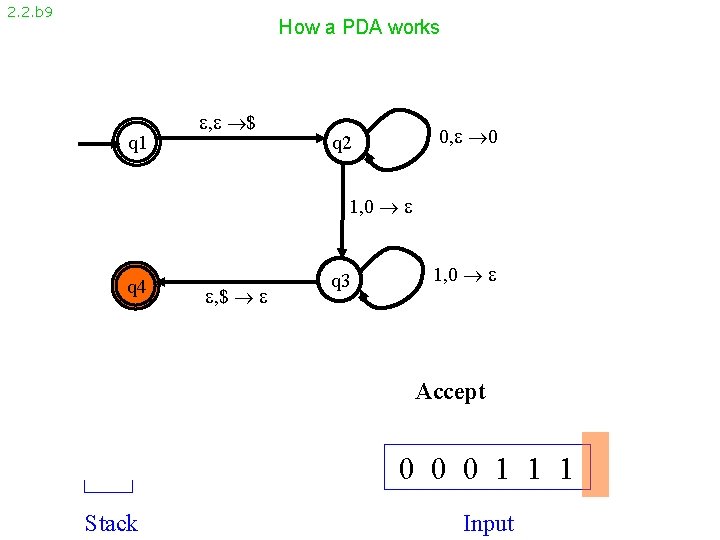
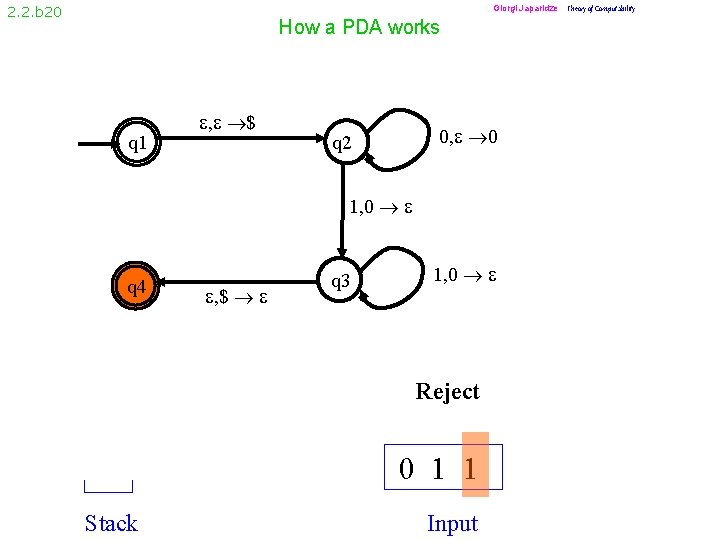
2. 2. b 9 How a PDA works q 1 , $ 0, 0 q 2 1, 0 q 4 , $ q 3 1, 0 Accept 0 0 0 1 1 1 Stack Input

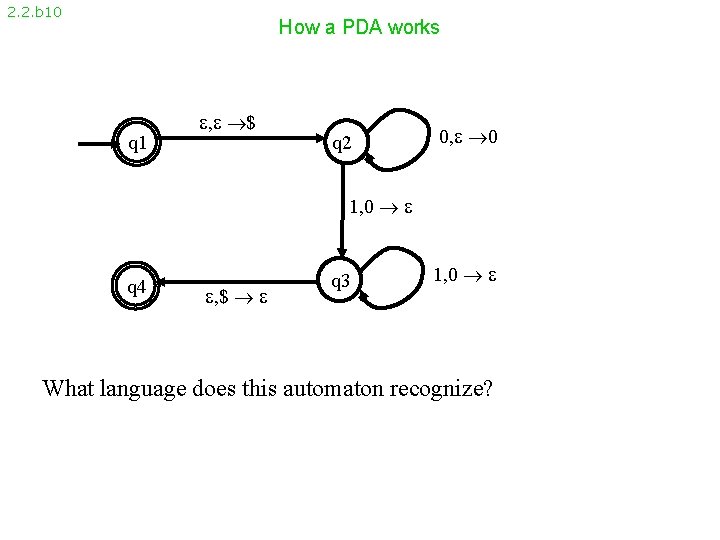
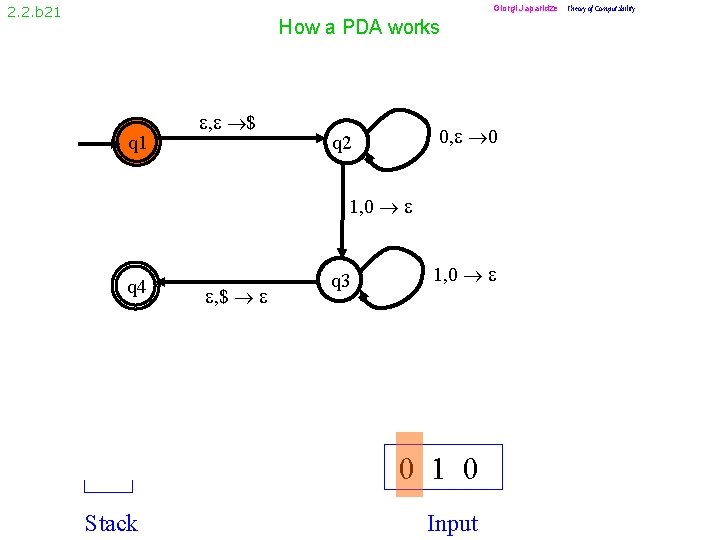
2. 2. b 10 How a PDA works q 1 , $ q 2 0, 0 1, 0 q 4 , $ q 3 1, 0 What language does this automaton recognize?

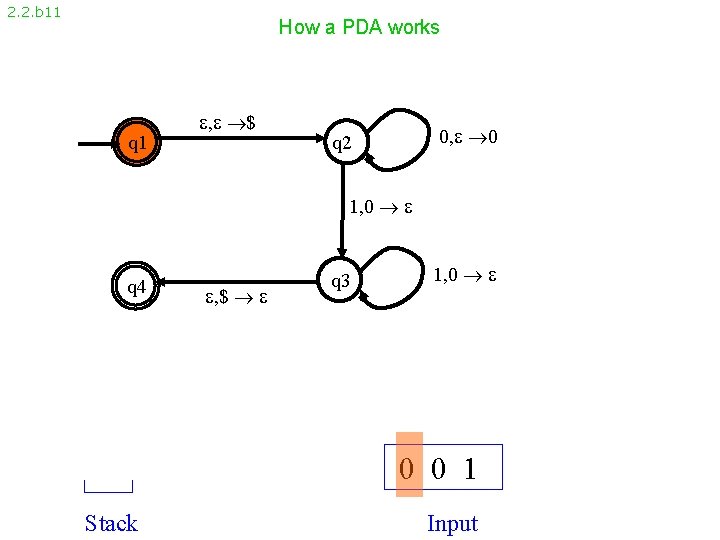
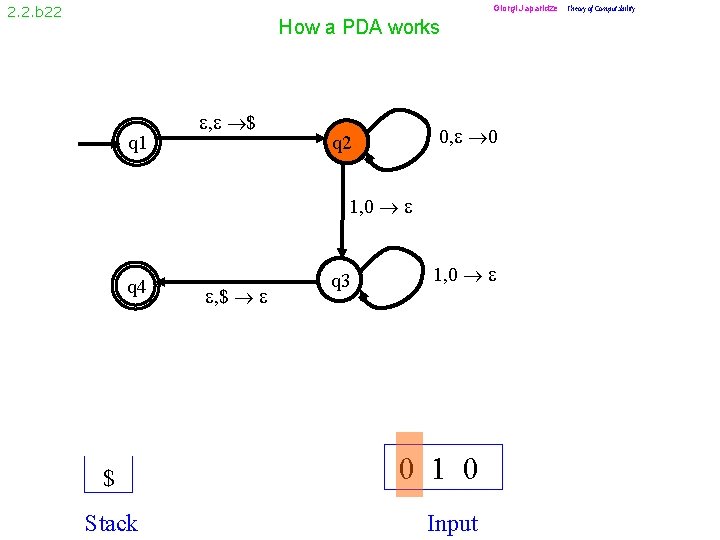
2. 2. b 11 How a PDA works q 1 , $ 0, 0 q 2 1, 0 q 4 , $ q 3 1, 0 0 0 1 Stack Input

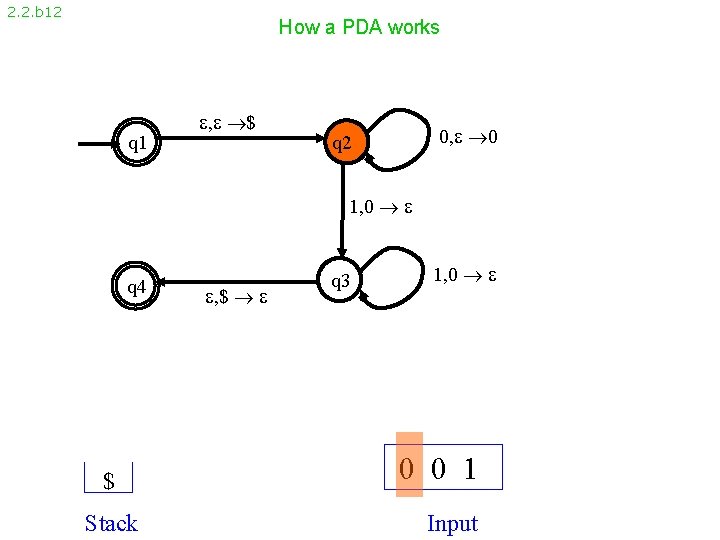
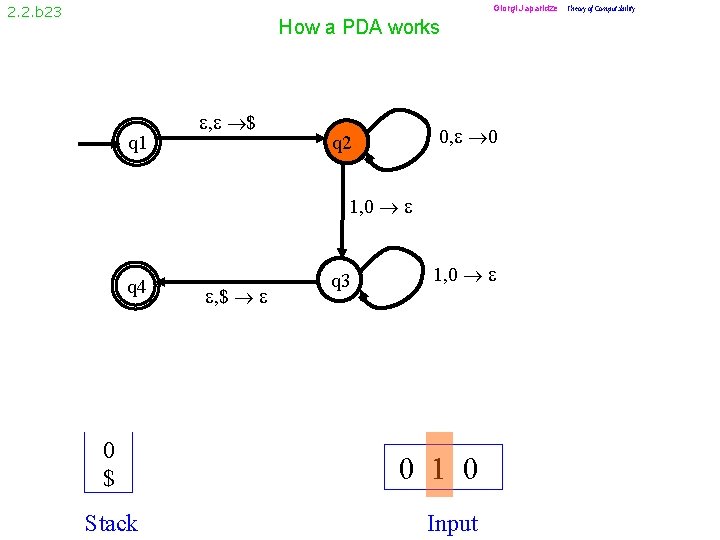
2. 2. b 12 How a PDA works q 1 , $ 0, 0 q 2 1, 0 q 4 $ Stack , $ q 3 1, 0 0 0 1 Input

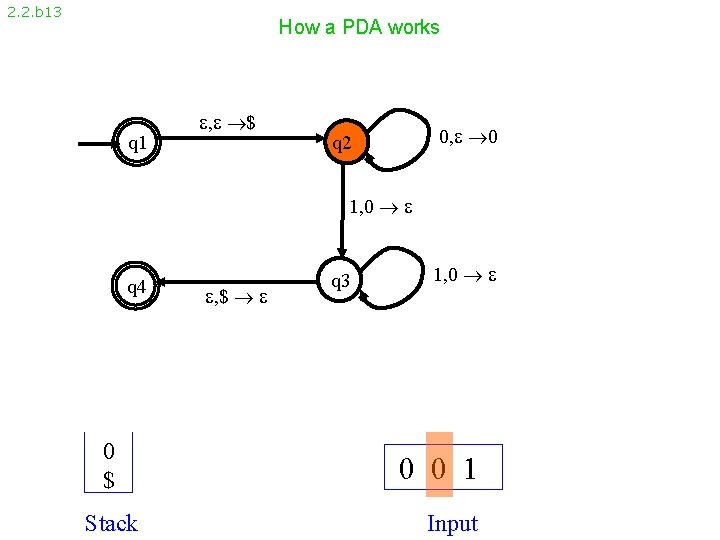
2. 2. b 13 How a PDA works q 1 , $ 0, 0 q 2 1, 0 q 4 0 $ Stack , $ q 3 1, 0 0 0 1 Input

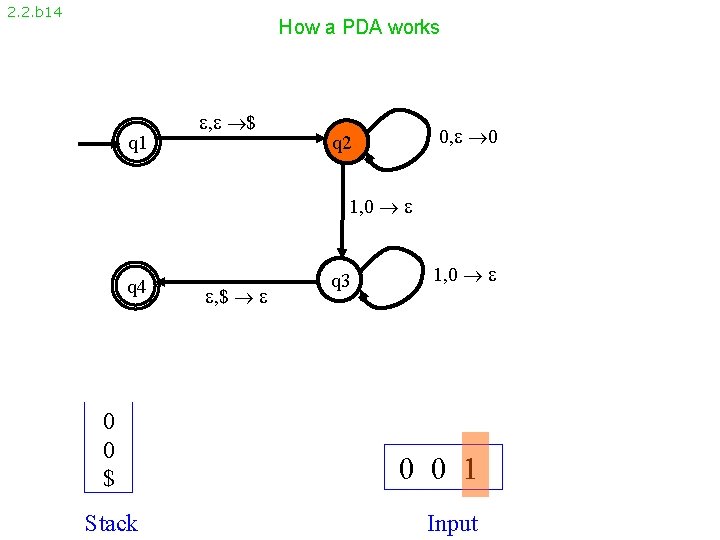
2. 2. b 14 How a PDA works q 1 , $ 0, 0 q 2 1, 0 q 4 0 0 $ Stack , $ q 3 1, 0 0 0 1 Input

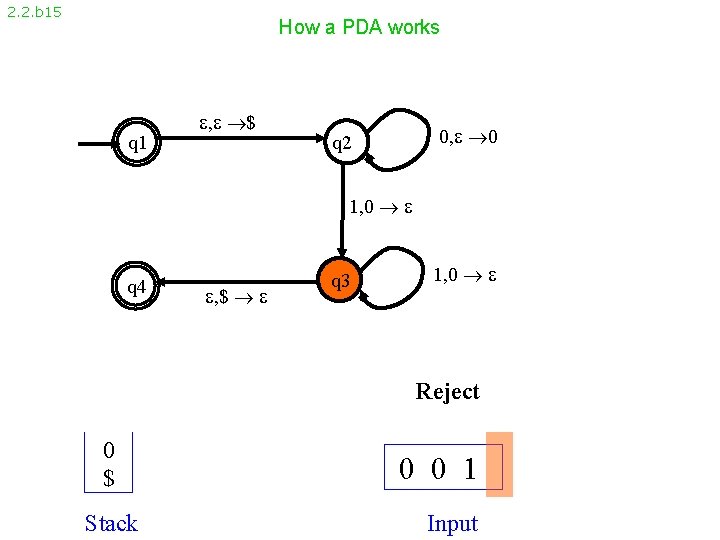
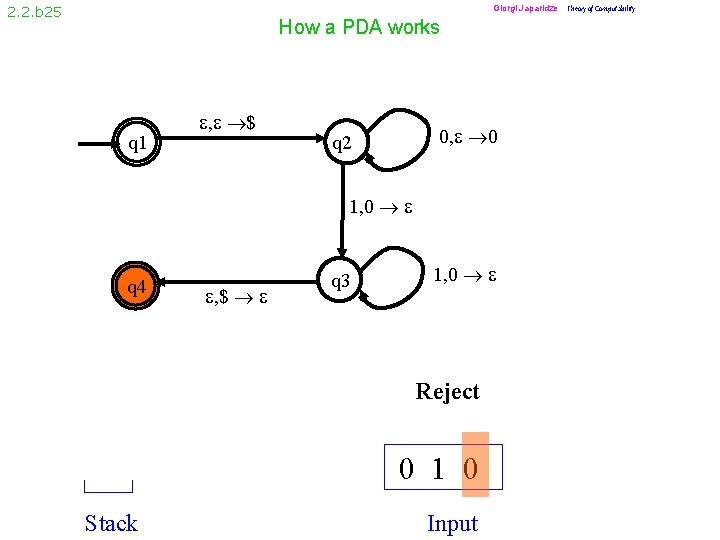
2. 2. b 15 How a PDA works q 1 , $ 0, 0 q 2 1, 0 q 4 , $ q 3 1, 0 Reject 0 $ Stack 0 0 1 Input

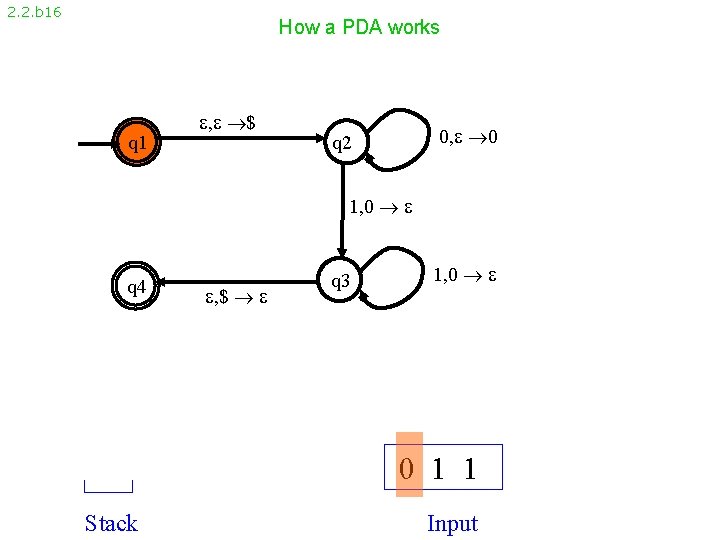
2. 2. b 16 How a PDA works q 1 , $ 0, 0 q 2 1, 0 q 4 , $ q 3 1, 0 0 1 1 Stack Input

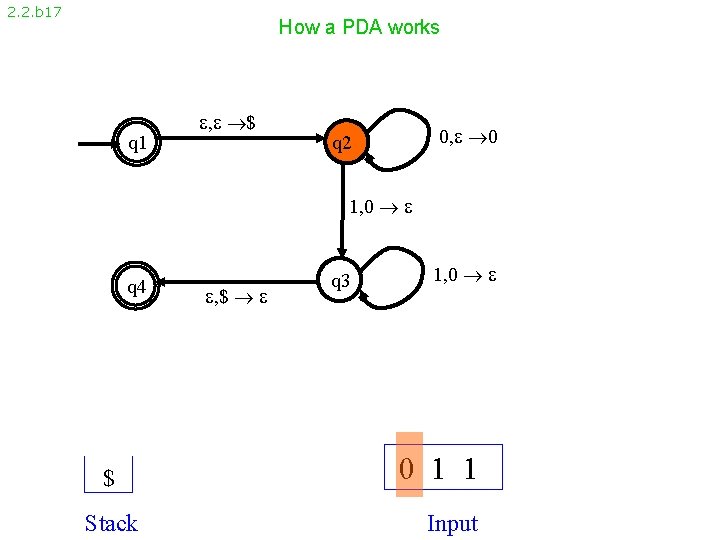
2. 2. b 17 How a PDA works q 1 , $ 0, 0 q 2 1, 0 q 4 $ Stack , $ q 3 1, 0 0 1 1 Input

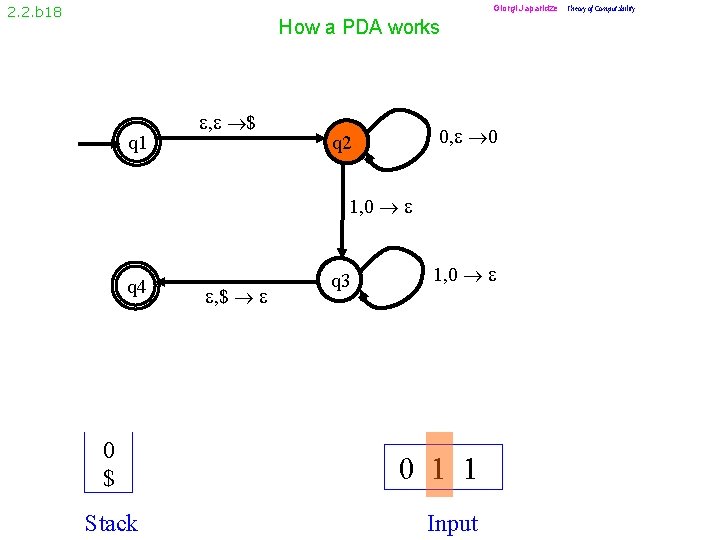
Giorgi Japaridze Theory of Computability 2. 2. b 18 How a PDA works q 1 , $ 0, 0 q 2 1, 0 q 4 0 $ Stack , $ q 3 1, 0 0 1 1 Input

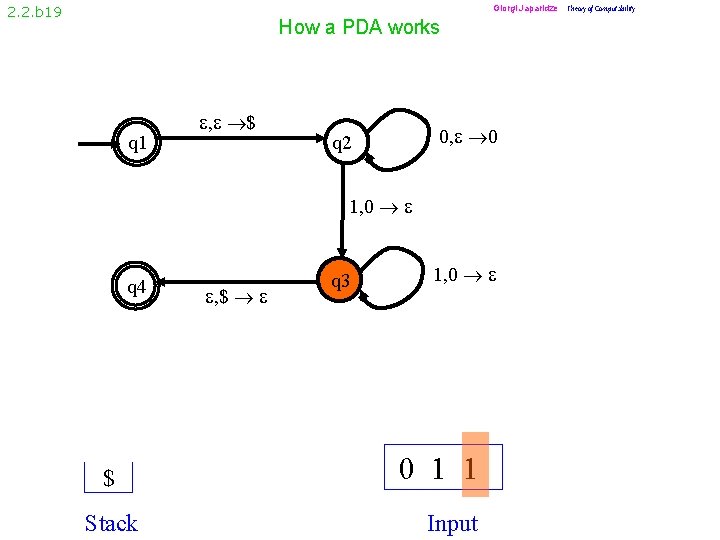
Giorgi Japaridze Theory of Computability 2. 2. b 19 How a PDA works q 1 , $ 0, 0 q 2 1, 0 q 4 $ Stack , $ q 3 1, 0 0 1 1 Input

Giorgi Japaridze Theory of Computability 2. 2. b 20 How a PDA works q 1 , $ 0, 0 q 2 1, 0 q 4 , $ q 3 1, 0 Reject 0 1 1 Stack Input

Giorgi Japaridze Theory of Computability 2. 2. b 21 How a PDA works q 1 , $ 0, 0 q 2 1, 0 q 4 , $ q 3 1, 0 0 1 0 Stack Input

Giorgi Japaridze Theory of Computability 2. 2. b 22 How a PDA works q 1 , $ 0, 0 q 2 1, 0 q 4 $ Stack , $ q 3 1, 0 0 1 0 Input

Giorgi Japaridze Theory of Computability 2. 2. b 23 How a PDA works q 1 , $ 0, 0 q 2 1, 0 q 4 0 $ Stack , $ q 3 1, 0 0 1 0 Input

Giorgi Japaridze Theory of Computability 2. 2. b 24 How a PDA works q 1 , $ 0, 0 q 2 1, 0 q 4 $ Stack , $ q 3 1, 0 0 1 0 Input

Giorgi Japaridze Theory of Computability 2. 2. b 25 How a PDA works q 1 , $ 0, 0 q 2 1, 0 q 4 , $ q 3 1, 0 Reject 0 1 0 Stack Input

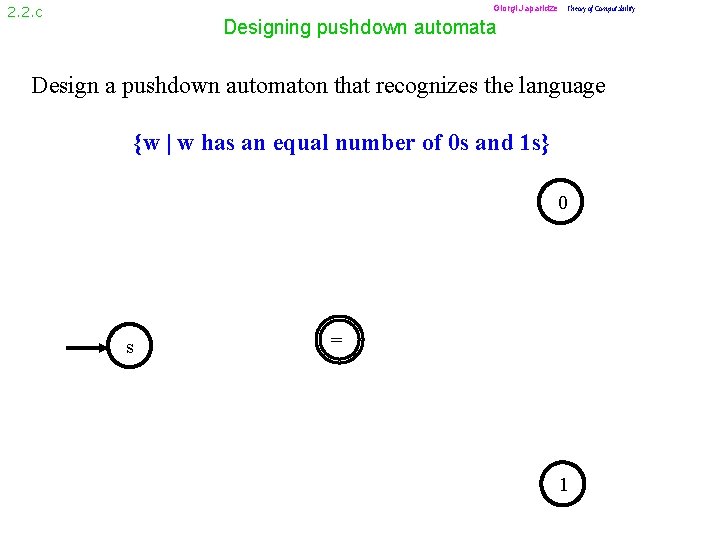
Giorgi Japaridze Theory of Computability 2. 2. c Designing pushdown automata Design a pushdown automaton that recognizes the language {w | w has an equal number of 0 s and 1 s} 0 s = 1

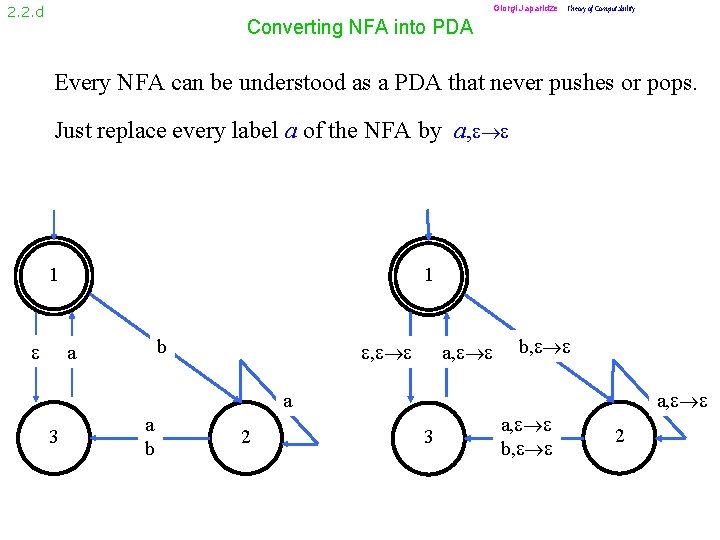
Giorgi Japaridze Theory of Computability 2. 2. d Converting NFA into PDA Every NFA can be understood as a PDA that never pushes or pops. Just replace every label a of the NFA by a, 1 1 b a , a, b, a 3 a b 2 a, 3 a, b, 2

2. 2. e Giorgi Japaridze Theory of Computability Main theorems Theorem 2. 20: A language is context-free iff some pushdown automaton recognizes it. Theorem: Not every nondeterministic PDA has an equivalent deterministic PDA. Example 2. 18: There is a nondeterministic PDA recognizing {ww. R | w {0, 1}* } (w. R means w reversed), but no deterministic PDA can recognize this language. Proofs omitted.

2. 3. a Giorgi Japaridze Theory of Computability The pumping lemma for context-free languages Theorem 2. 34 (Pumping lemma for context-free languages) If L is a context-free language, then there is a number p (the pumping length) where, if s is any string in L of length at least p, then s may be divided into five pieces s = uvxyz satisfying the conditions: 1. For each i 0, uvixyiz L; 2. |vy| > 0; 3. |vxy| p. uxz uvxyz uvvxyyz uvvvxyyyz uvvvvxyyyyz uvvvvvxyyyyyz

2. 3. b Giorgi Japaridze Theory of Computability The pumping lemma in work: example S “R” is a regular expression R 0 | ( R )* “ 0” is a regular expression “(0)*” is a regular expression “((0)*)*” is a regular expression “(((0)*)*)*” is a regular expression … “((0)*)*” is a regular expression uv 0 xy 0 z: uv 1 xy 1 z: uv 2 xy 2 z: uv 3 xy 3 z: u = “( v=( x=0 y = )* z = )*” is a regular expression “(0)*” is a regular expression “((0)*)*” is a regular expression “(((0)*)*)*” is a regular expression “((((0)*)*” is a regular expression

2. 3. c Giorgi Japaridze Theory of Computability Using the pumping lemma for proving that certain languages are not CF Example 2. 36: Show that the following language is not CF: B = {anbncn | n 0} Proof by contradiction: Assume B is CF. Let then p be its pumping length. Select w B with |w| p. By the pumping lemma, w=uvxyz and v and y can be pumped. If either v or y contain more than one type of symbols, then pumping would intermix these symbols in a wrong way. aaaabbbbcccc B aaaababbbbccccc B Thus, one of the three symbols should be neither in neither v, nor in y. aaaabbbbcccc B But then, after pumping, the number of that symbol will not change, while the number of the other symbols will increase. aaaaaabbbbcccc B

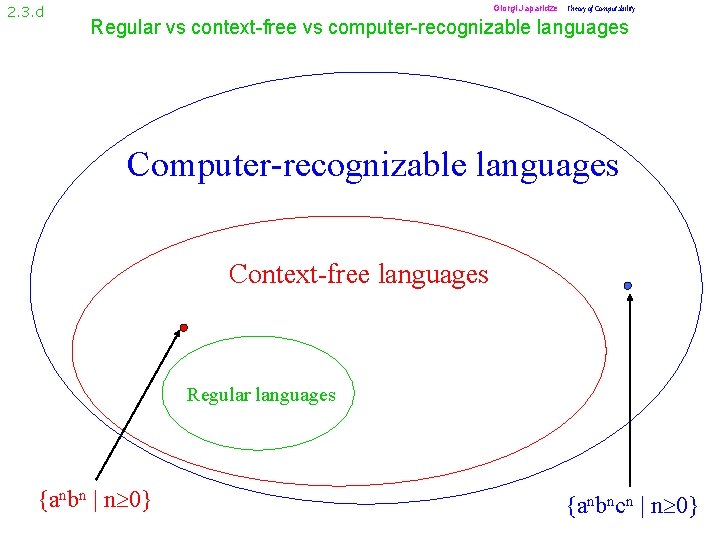
2. 3. d Giorgi Japaridze Theory of Computability Regular vs context-free vs computer-recognizable languages Context-free languages Regular languages {anbn | n 0} {anbncn | n 0}