CONTEXTFREE GRAMMARS A contextfree grammar CFG is a

CONTEXT-FREE GRAMMARS วตถประสงค A context-free grammar (CFG) is a simple recursive method of specifying grammar rules by which strings in a language can be generated. To a large extent, they are capable of specifying the syntax of high-level programming languages and other formal languages.

การนยามภาษา CONTEXT-FREE GRAMMARS DESCRIBE THE LANGUAGES Using recursive definition to describe any languages (regular or nonregular). Example, palindrome language. Alphabet = { a, b} Rule 1: , a, b PALINDROME Rule 2: For any S PALINDROME, then a. Sa, b. Sb are in PALINDROME. Note: S can be considered as a variable, representing an arbitrary element of PALINDROME.

การนยามภาษา CONTEXT-FREE GRAMMARS DESCRIBE THE LANGUAGES Alphabet = { a, b} Rule 1: , a, b PALINDROME Rule 2: For any S PALINDROME, then a. Sa, b. Sb are in PALINDROME. S can be considered as a variable, representing an arbitrary element of PALINDROME. Rule can be considered as a relation, representing a transformation, denoted by “ ”. Rule 1: S | a | b Rule 2: S a. Sa | b. Sb inals. m r e t e ble. a d b ar i r n a a v a r , inal o m r e t n o S is a n Note: The vertical bar “|” means “or”.

CONTEXT-FREE GRAMMARS ���� DESCRIBE THE LANGUAGES ตวแปร The production of the grammar S Start variable. others represent some auxiliary class of strings. (class of recursive definition).

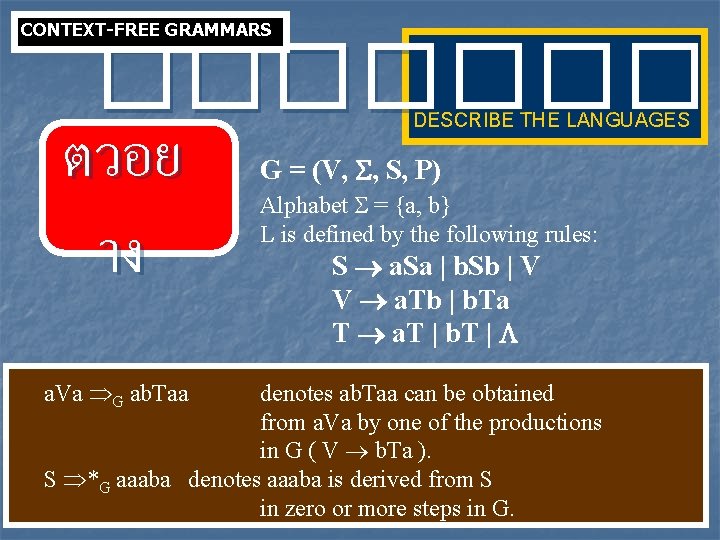
CONTEXT-FREE GRAMMARS ���� ตวอย าง DESCRIBE THE LANGUAGES Alphabet = {a, b} L is defined by the following rules: S a. Sa | b. Sb | V V a. Tb | b. Ta T a. T | b. T | NO NP A LIN DR O Some words generated by these rules, S a. Sa a. Va ab. Taa abaa. S a. Sa ab. Sba ab. Vba aba. Tbba abaabba. ME

CONTEXT-FREE GRAMMARS ���� DESCRIBE THE LANGUAGES นยาม A context-free grammar (CFG) is a 4 -tiple G = (V, , S, P) where V and are disjoint finite sets, S is an element of V and P is a finite set of formulas of the form A , where A V and (V )*. S: start symbol V: set of variables or nonterminals : alphabet or set of terminals. P: set of grammar rules or productions.

CONTEXT-FREE GRAMMARS ���� ตวอย าง a. Va G ab. Taa DESCRIBE THE LANGUAGES G = (V, , S, P) Alphabet = {a, b} L is defined by the following rules: S a. Sa | b. Sb | V V a. Tb | b. Ta T a. T | b. T | denotes ab. Taa can be obtained from a. Va by one of the productions in G ( V b. Ta ). S *G aaaba denotes aaaba is derived from S in zero or more steps in G.

CONTEXT-FREE GRAMMARS ���� คำศ พธ DESCRIBE THE LANGUAGES Let G = (V, , S, P) be a CFG. The language generated by G is L(G) = { x * | S *G x }. A language L is a Context-free language (CFL) if there is a CFG G so that L = L(G). A string x (V )* is a sentential if there is a derivation A string x * is a S *G x in G. sentence of G if there is a derivation form of G S *G x in G.

CONTEXT-FREE GRAMMARS ���� DESCRIBE THE LANGUAGES ปญหา To demonstrate that a CFG generates a language, we must show two things: 1. every string in the language can be derived from the grammar 2. no other string can be.

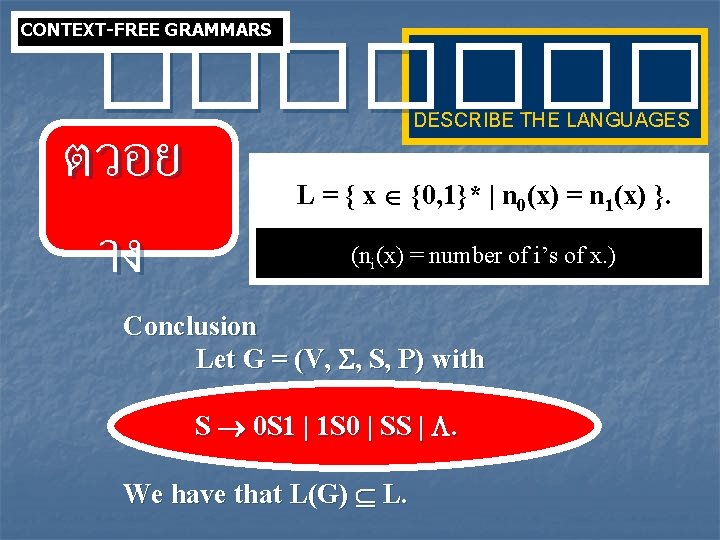
CONTEXT-FREE GRAMMARS ���� ตวอย าง DESCRIBE THE LANGUAGES L = { x {0, 1}* | n 0(x) = n 1(x) }. (ni(x) = number of i’s of x. ) Clearly that is in this language. Rule 1: S One way to produce other strings in L, add one 0 and one 1. Rule 2: S 0 S 1 Rule 3: S 1 S 0 Consider strings which do not start and end with the same symbol. Example, 01110100 or 10010110 These strings can be obtained by the concatenation of two strings in L. Rule 4: S SS. Example, 01110100 can be obtained from 01 and 110100.

CONTEXT-FREE GRAMMARS ���� ตวอย าง DESCRIBE THE LANGUAGES L = { x {0, 1}* | n 0(x) = n 1(x) }. (ni(x) = number of i’s of x. ) Conclusion Let G = (V, , S, P) with S 0 S 1 | 1 S 0 | SS | . We have that L(G) L.

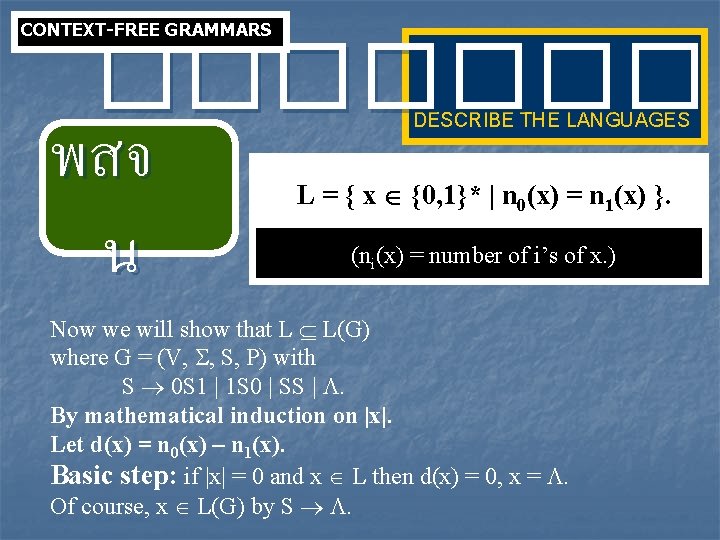
CONTEXT-FREE GRAMMARS ���� พสจ น DESCRIBE THE LANGUAGES L = { x {0, 1}* | n 0(x) = n 1(x) }. (ni(x) = number of i’s of x. ) Now we will show that L L(G) where G = (V, , S, P) with S 0 S 1 | 1 S 0 | SS | . By mathematical induction on |x|. Let d(x) = n 0(x) – n 1(x). Basic step: if |x| = 0 and x L then d(x) = 0, x = . Of course, x L(G) by S .

CONTEXT-FREE GRAMMARS ���� พสจ น DESCRIBE THE LANGUAGES L = { x {0, 1}* | n 0(x) = n 1(x) }. (ni(x) = number of i’s of x. ) Inductive step: for |x|≤ k, d(x) = 0, x L. Let x L and |x| = k+1. Case 1: x begins with 0, ends with 1, then x = 0 y 1 and y L(G). Then S *G y. Since S 0 S 1, we also have x L(G). Case 2: x begins with 1, ends with 0, similar to the case 1. Case 3: x begins with 1, ends with 1, then x = 1 y 1 and d(x) = 0. d(1) = -1 and d(1 y) = 1, then u such that u is a prefix of 1 y, d(u) = 0. x = uw, u and w L and L(G). Since S SS, x L(G). Case 4: x begins with 0, ends with 0, similar to the case 3. Q. E. D.

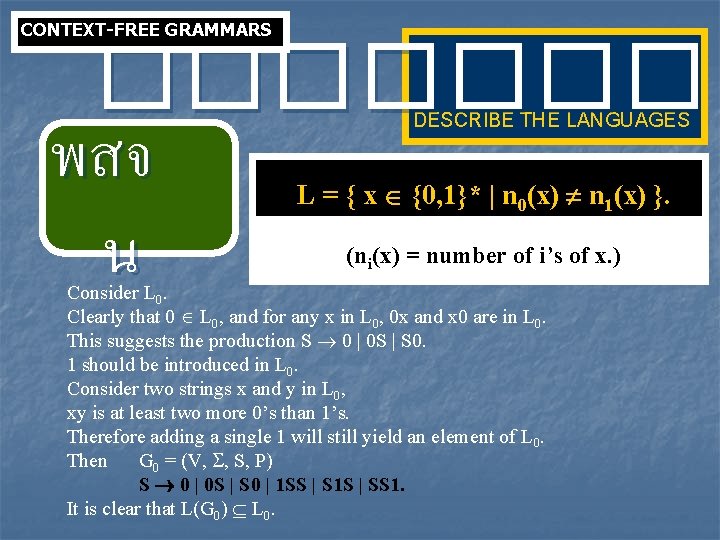
CONTEXT-FREE GRAMMARS ���� ตวอย าง Let L 0 be Let L 1 be DESCRIBE THE LANGUAGES L = { x {0, 1}* | n 0(x) n 1(x) }. (ni(x) = number of i’s of x. ) the language of strings with more 0’s than 1’s. the language of strings with more 1’s than 0’s. Then L = L 0 L 1.

CONTEXT-FREE GRAMMARS ���� พสจ น DESCRIBE THE LANGUAGES L = { x {0, 1}* | n 0(x) n 1(x) }. (ni(x) = number of i’s of x. ) Consider L 0. Clearly that 0 L 0, and for any x in L 0, 0 x and x 0 are in L 0. This suggests the production S 0 | 0 S | S 0. 1 should be introduced in L 0. Consider two strings x and y in L 0, xy is at least two more 0’s than 1’s. Therefore adding a single 1 will still yield an element of L 0. Then G 0 = (V, , S, P) S 0 | 0 S | S 0 | 1 SS | S 1 S | SS 1. It is clear that L(G 0) L 0.

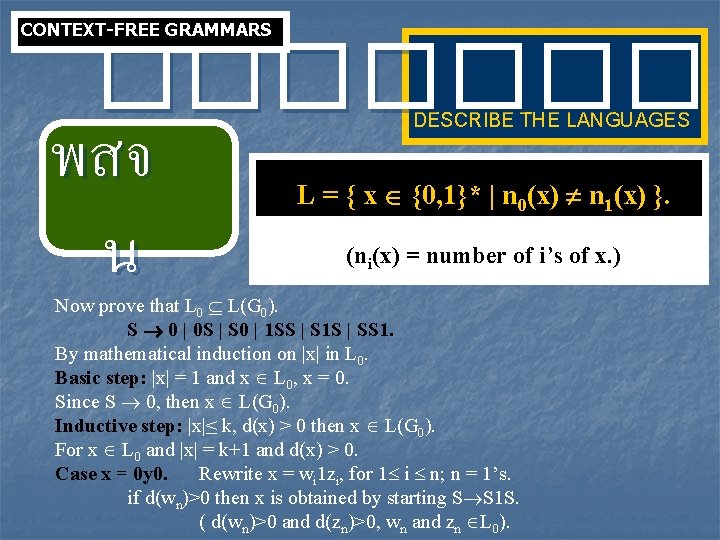
CONTEXT-FREE GRAMMARS ���� พสจ น DESCRIBE THE LANGUAGES L = { x {0, 1}* | n 0(x) n 1(x) }. (ni(x) = number of i’s of x. ) Now prove that L 0 L(G 0). S 0 | 0 S | S 0 | 1 SS | S 1 S | SS 1. By mathematical induction on |x| in L 0. Basic step: |x| = 1 and x L 0, x = 0. Since S 0, then x L(G 0). Inductive step: |x|≤ k, d(x) > 0 then x L(G 0). For x L 0 and |x| = k+1 and d(x) > 0. Case x = 0 y 0. Rewrite x = wi 1 zi, for 1 i n; n = 1’s. if d(wn)>0 then x is obtained by starting S S 1 S. ( d(wn)>0 and d(zn)>0, wn and zn L 0).

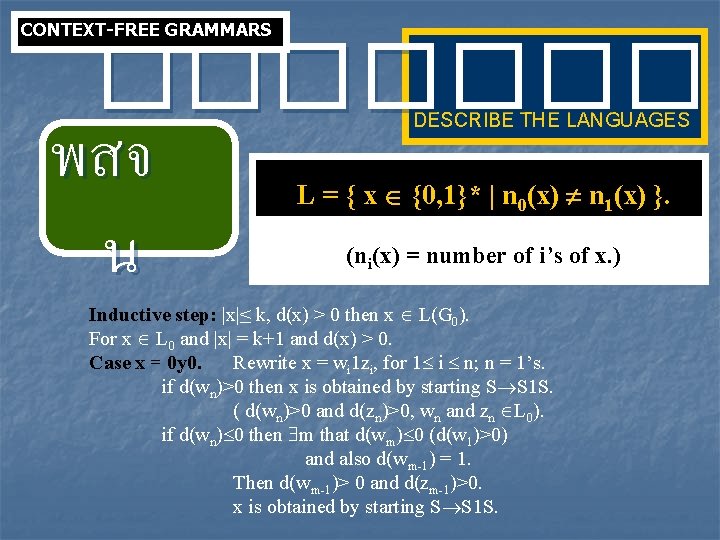
CONTEXT-FREE GRAMMARS ���� พสจ น DESCRIBE THE LANGUAGES L = { x {0, 1}* | n 0(x) n 1(x) }. (ni(x) = number of i’s of x. ) Inductive step: |x|≤ k, d(x) > 0 then x L(G 0). For x L 0 and |x| = k+1 and d(x) > 0. Case x = 0 y 0. Rewrite x = wi 1 zi, for 1 i n; n = 1’s. if d(wn)>0 then x is obtained by starting S S 1 S. ( d(wn)>0 and d(zn)>0, wn and zn L 0). if d(wn) 0 then m that d(wm) 0 (d(w 1)>0) and also d(wm-1) = 1. Then d(wm-1)> 0 and d(zm-1)>0. x is obtained by starting S S 1 S.

CONTEXT-FREE GRAMMARS ���� พสจ น DESCRIBE THE LANGUAGES L = { x {0, 1}* | n 0(x) n 1(x) }. (ni(x) = number of i’s of x. ) Context-free grammar of this language is the following: S A|B A 0 | 0 A | 1 AA | A 1 A | AA 1 B 1 | 1 B | 0 BB | B 0 B | BB 0

CONTEXT-FREE GRAMMARS ���� ตวอย าง DESCRIBE THE LANGUAGES ALGEBRAIC EXPRESSION Context-free grammar of this language is the following: S S+S | S-S | S S | (S) | a where a is a terminal symbol.

���� �� ทฤษฎบ CONTEXT-FREE GRAMMARS CONTEXT-FREE LANGUAGES ท For any context-free languages L 1 and L 2, the languages L 1 L 2, L 1 L 2 and L 1* are also context-free languages.

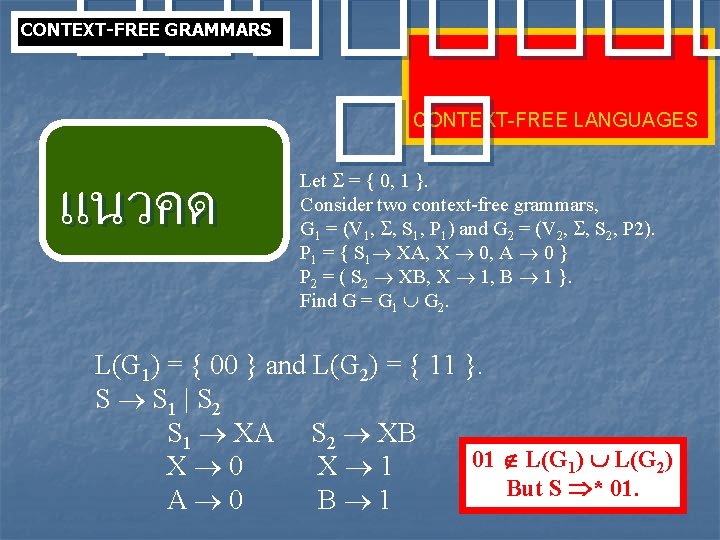
���� �� CONTEXT-FREE GRAMMARS CONTEXT-FREE LANGUAGES แนวคด Let = { 0, 1 }. Consider two context-free grammars, G 1 = (V 1, , S 1, P 1) and G 2 = (V 2, , S 2, P 2). P 1 = { S 1 XA, X 0, A 0 } P 2 = ( S 2 XB, X 1, B 1 }. Find G = G 1 G 2. L(G 1) = { 00 } and L(G 2) = { 11 }. S S 1 | S 2 S 1 XA S 2 XB 01 L(G 1) L(G 2) X 0 X 1 But S * 01. A 0 B 1

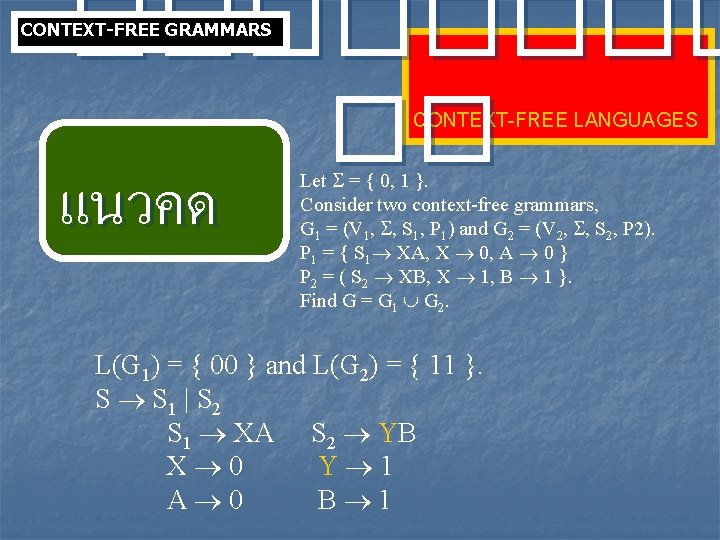
���� �� CONTEXT-FREE GRAMMARS CONTEXT-FREE LANGUAGES แนวคด Let = { 0, 1 }. Consider two context-free grammars, G 1 = (V 1, , S 1, P 1) and G 2 = (V 2, , S 2, P 2). P 1 = { S 1 XA, X 0, A 0 } P 2 = ( S 2 XB, X 1, B 1 }. Find G = G 1 G 2. L(G 1) = { 00 } and L(G 2) = { 11 }. S S 1 | S 2 S 1 XA S 2 YB X 0 Y 1 A 0 B 1

���� �� ทฤษฎบ CONTEXT-FREE GRAMMARS CONTEXT-FREE LANGUAGES ท For any context-free languages L 1 and L 2, the languages L 1 L 2, L 1 L 2 and L 1* are also context-free languages.

���� �� ทฤษฎบ CONTEXT-FREE GRAMMARS CONTEXT-FREE LANGUAGES ท Case: L 1 L 2 V = V 1 V 2 { S } P = P 1 P 2 { S S 1 | S 2 } Case: L 1 L 2 V = V 1 V 2 { S } P = P 1 P 2 { S S 1 S 2 } Case: L 1* V = V 1 { S } P = P 1 { S S 1 S | }

���� �� CONTEXT-FREE GRAMMARS CONTEXT-FREE LANGUAGES Is every regular language a context-free language ?

���� �� ���� CONTEXT-FREE GRAMMARS CONTEXT-FREE LANGUAGES ��� e e r f t x e t n o c a s i e g a u g n a l r a l u g e r Every language. By definition of regular language, , { }and { a } are regular languages, and regular is closed under union, concatenation and Kleene’s star. To prove this theorem, we have to show that any regular can be produced by some context-free grammars.

���� �� ตวอย CONTEXT-FREE GRAMMARS CONTEXT-FREE LANGUAGES าง Regular language (011+1)*(01)* From the regular expression, we have S XY X represents (011+1)* Y represents (01)* X 011 X | Y 01 Y | Example: 01110101 can be derived from CFG.

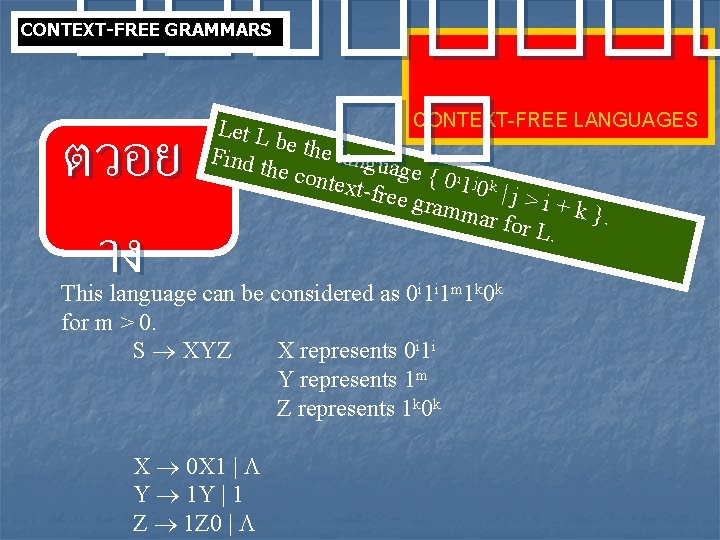
���� �� ตวอย CONTEXT-FREE GRAMMARS าง CONTEXT-FREE LANGUAGES Let L be the l Find t he con anguage { 0 i j text-fr 1 k ee gra 0 | j > i + mmar k }. for L. This language can be considered as 0 i 1 i 1 m 1 k 0 k for m > 0. S XYZ X represents 0 i 1 i Y represents 1 m Z represents 1 k 0 k X 0 X 1 | Y 1 Y | 1 Z 1 Z 0 |

���� �� ���� CONTEXT-FREE GRAMMARS CONTEXT-FREE LANGUAGES �� Understanding the sentence begins with understanding its grammatical structure ( i. e. , knowing how it is derived from the grammar rules ). T A V I R E D E E R T N IO

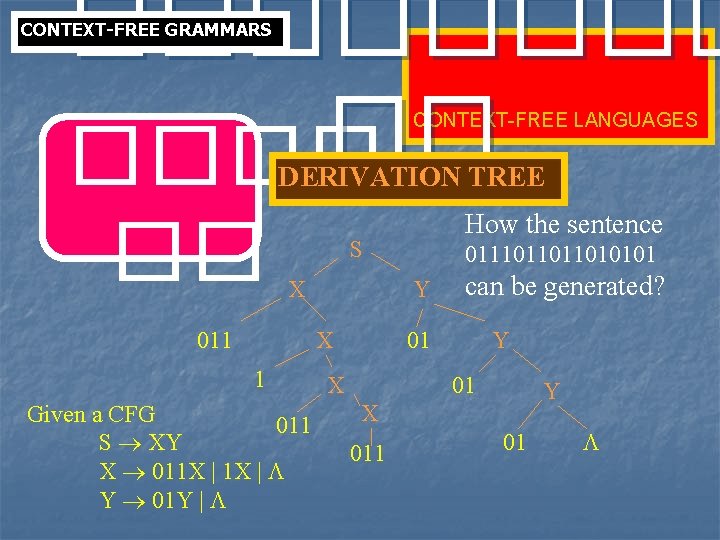
���� �� ���� CONTEXT-FREE GRAMMARS CONTEXT-FREE LANGUAGES DERIVATION TREE �� How the sentence S X 011 Y X 1 Given a CFG 011 S XY X 011 X | Y 01 Y | 0111011011010101 can be generated? 01 X Y 01 Y X 011 01

���� �� ���� CONTEXT-FREE GRAMMARS CONTEXT-FREE LANGUAGES DERIVATION TREE �� ความกำกวม AMBIGUOUS A context-free grammar G is ambiguous if there is at least one string in L(G) having two or more distinct derivation trees.

���� �� ���� CONTEXT-FREE GRAMMARS CONTEXT-FREE LANGUAGES �� ความกำกวม AMBIGUOUS Given a context-free grammar G with = { a, + } and S S+S|a The sentence a+a+a is in L(G) which has two derivations. S S+S a+S+S a+a+a S S+S+S a+a+S a+a+a This language is ambiguous.

โจทย นาคด Let G be a context-free and x n. G y be a derivation in G where x can be written x = y 1 A 1 y 2 A 2…yk. Akyk+1 with yi *. Show that there are strings pi ( V)* that satisfy 1. Ai ti pi. 2. y = y 1 p 1 y 2 p 2…ykpkyk+1 3. Sum of all ti (1 i k) = n. ?

���� �� ตวอย CONTEXT-FREE GRAMMARS CONTEXT-FREE LANGUAGES Given a context-free grammar G with S if E S | if E S else S | S This language is ambiguous. าง if exp 1 if exp 2 statement 1 else statement 2 exp 1 exp 2 S S if E S else S if E S statement 2 statement 1 exp 2 PA R BE ENTH TH USED ESES EA MB TO RE CAN IGU M ITY OVE if E S else S statement 2 statement 1

���� �� ตวอย CONTEXT-FREE GRAMMARS CONTEXT-FREE LANGUAGES าง Given a context-free grammar G with S S + S| S S | a This language is ambiguous. Theorem The context-free grammar G 1 with productions S S+T|T T T F|F F (S) | a is unambiguous.

NORMAL FORMS

������ �� NORMAL FORMS Ambiguity is one undesirable property of a context-free grammar that we might wish to Eliminate. In this section we discuss some more straightforward ways of “improving” a grammar without changing the resulting language.

������ �� NORMAL FORMS We try to eliminate “ -productions”, of the form A , and unit productions, ” in which one variable is simply replaced by another. REMARK : production G If there are no -productions, | |. If there are no unit productions, if | | = | | then this step consists of replacing a variable by a single terminal.

������ �� NORMAL FORMS We try to eliminate “ -productions”, of the form A , and unit productions, ” in which one variable is simply replaced by another. Let L be the length of the current string. Let T be the number of terminals of the current string. For any string x Language, of length k, then L+T = 2 k. That is the number of steps S G x is at most 2 k-1 steps.

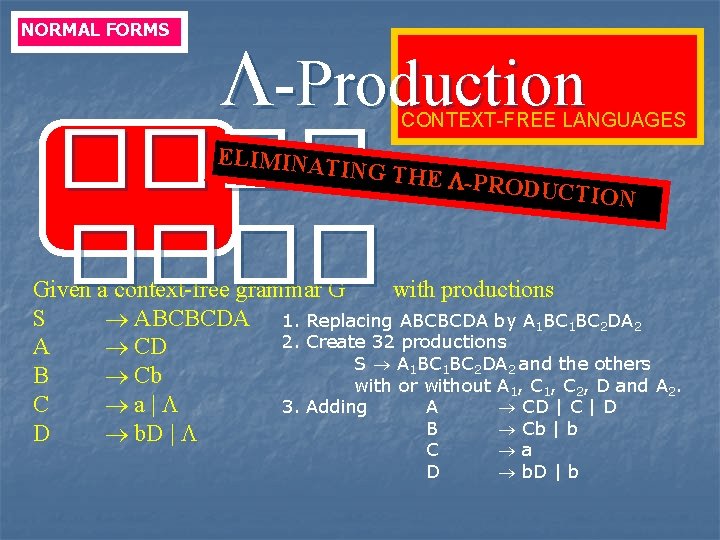
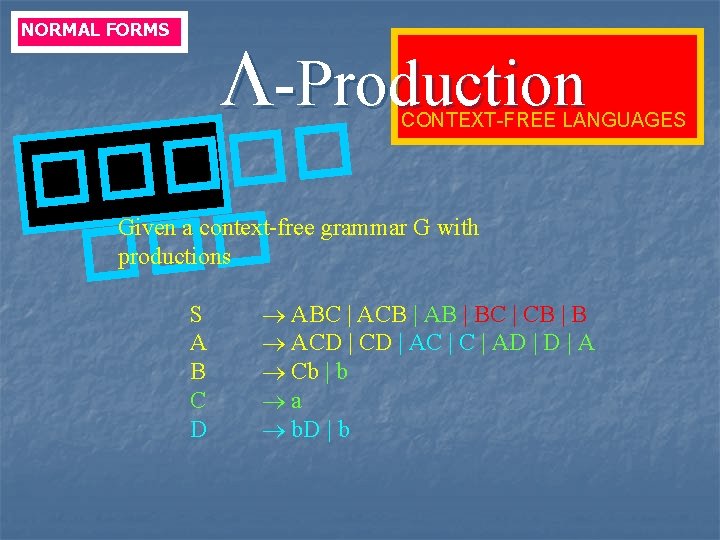
NORMAL FORMS -Production ���� CONTEXT-FREE LANGUAGES ELIMINAT ING THE -PRODUCT ION Given a context-free grammar G with productions S ABCBCDA 1. Replacing ABCBCDA by A 1 BC 2 DA 2 2. Create 32 productions A CD S A 1 BC 2 DA 2 and the others B Cb with or without A 1, C 2, D and A 2. C a| 3. Adding A CD | C | D B Cb | b D b. D | C D a b. D | b

NORMAL FORMS -Production ���� � CONTEXT-FREE LANGUAGES NULLABL E A nullable variable in a context-free grammar G = ( V, , S, P ) is defined as follows: 1. Any variable A for which P contains the production A is nullable. 2. If A B 1 B 2…Bn and B 1, B 2, …, Bn are nullables, then A is also nullable. 3. No other variables in V are nullable. A is nullable if and only if A *G

NORMAL FORMS -Production ����� CONTEXT-FREE LANGUAGES Algorithm: Find. Null N 0 = { A V | P contains the production A }; j = 0; Do j = j + 1; Nj = Nj-1 { A | P contains A B that B Nj-1* } While Nj Nj-1; Nj is the set of all nullable variables. From the previous example, N 0 = { C, D } and N 1 = { A, C, D }.

NORMAL FORMS -Production ����� CONTEXT-FREE LANGUAGES Algorithm: R emove. Null Given a CFG G=(V, , S, P), construct a CFG G 1=(V, , S, P 1) without -productions as follows: Initialize P 1 to be P. Find all nullable variables in V, using Find. Null. For every A in P, add to P 1 every production that can be obtained form this one by deleting from or more the occurrences in of nullable variables. Delete all -production from P 1. Delete any duplicates. Delete productions of the from A A.

NORMAL FORMS -Production � �� � CONTEXT-FREE LANGUAGES Given a context-free grammar G with productions S A B C D ABC | ACB ACD | CD Cb a| b. D |

NORMAL FORMS -Production � �� � CONTEXT-FREE LANGUAGES Given a context-free grammar G with productions S A B C D ABC | ACB ACD | CD Cb a| b. D |

NORMAL FORMS -Production � �� � CONTEXT-FREE LANGUAGES Given a context-free grammar G with productions S A B C D ABC | ACB ACD | AC | C Cb a| b. D | b

NORMAL FORMS -Production � �� � CONTEXT-FREE LANGUAGES Given a context-free grammar G with productions S A B C D ABC | ACB ACD | AC | C Cb a| b. D | b

NORMAL FORMS -Production � �� � CONTEXT-FREE LANGUAGES Given a context-free grammar G with productions S A B C D ABC | ACB | AB ACD | AC | AD | A | Cb | b a b. D | b

NORMAL FORMS -Production � �� � CONTEXT-FREE LANGUAGES Given a context-free grammar G with productions S A B C D ABC | ACB | AB ACD | AC | AD | A | Cb | b a b. D | b

NORMAL FORMS -Production � �� � CONTEXT-FREE LANGUAGES Given a context-free grammar G with productions S A B C D ABC | ACB | AB | BC | CB | B ACD | AC | AD | A Cb | b a b. D | b

NORMAL FORMS -Production ����� �� CONTEXT-FREE LANGUAGES Context-fre e grammar Let G = ( V, , S, P ) be a context-free grammar, and let G 1 = ( V, , S, P ) be a context-free grammar obtained from G by Algorithm Remove. Null. Then G 1 has no -productions, and L(G 1) = L(G) – { }.

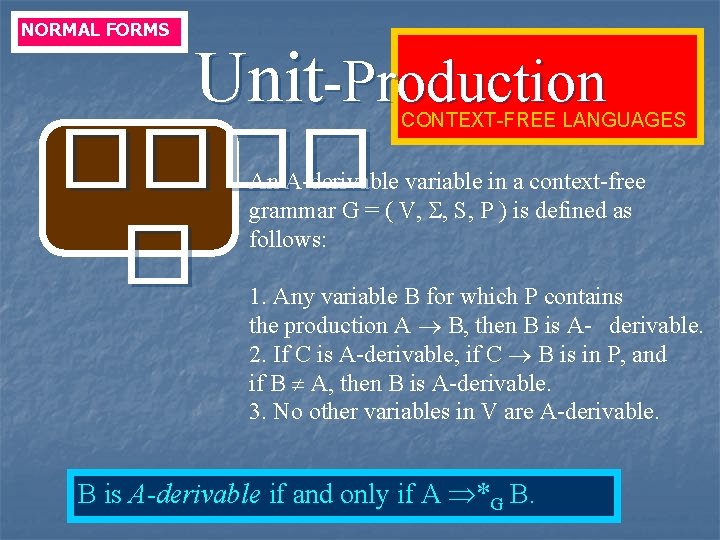
NORMAL FORMS Unit-Production ���� � CONTEXT-FREE LANGUAGES We try to eliminate “unit productions”, of the form A B, and A G* B. Suppose that the context-free grammar G has no -productions. Unit productions

NORMAL FORMS Unit-Production ���� � CONTEXT-FREE LANGUAGES An A-derivable variable in a context-free grammar G = ( V, , S, P ) is defined as follows: 1. Any variable B for which P contains the production A B, then B is A- derivable. 2. If C is A-derivable, if C B is in P, and if B A, then B is A-derivable. 3. No other variables in V are A-derivable. B is A-derivable if and only if A *G B.

NORMAL FORMS Algorithm Remove. Unit REMOVING THE UNIT PRODUCTIONS FROM A CFG. Given a CFG G=(V, , S, P) without -productions, construct a CFG G 1=(V, , S, P 1) having no unit productions as follows: Initialize P 1 to be P. For each A in V, find the set of all A-derivable variables. For every pair (A, B) such that B is A-derivable, and every non-unit production B , add the production A to P 1. Delete all unit productions from P 1.

NORMAL FORMS THEOREM Let G = ( V, , S, P ) be a context-free grammar with no -productions, and let G 1 = ( V, , S, P ) be a context-free grammar obtained from G by Algorithm Remove. Unit. Then G 1 contains no unit productions, and L(G 1) = L(G).

NORMAL FORMS EXAMPLE Given a context-free grammar G without -productions, and with productions S T F S+T|T T F|F (S) | a S-derivable = { T, F } T-derivable = { F } Productions in P 1 S S + T | T F | (S) | a T T F | (S) | a F (S) | a

NORMAL FORMS CHOMSKY NORMAL FORM Eliminating specific types of productions, such as -productions and unit productions, it may also be useful to impose restrictions on the form of the remaining productions. Several types of “Normal forms” have been introduced; we shall present one of them, the Chomsky normal form.

NORMAL FORMS CNF CHOMSKY NORMAL FORM Definition A context-free grammar G = ( V, , S, P ) is in Chomsky normal form if every production is of one of these two types: A BC A a where A, B and C are variables, and a is a terminal symbol.

NORMAL FORMS CNF CHOMSKY NORMAL FORM Construct a CFG in CNF Given context-free grammar G = ( V, , S, P ) Construct G 1 = ( V, , S, P 1 ) with no -productions and with no unit productions. Construct G 2 = ( V 2, , S, P 2 ) with productions A B 1 B 2…Bk , for k 2 A a Replace A B 1 B 2…Bk by A B 1 X 1, X 1 B 2 X 2, …, Xk-1 Bk-1 Bk

NORMAL FORMS EXAMPLE Given a context-free grammar G with productions S A B C D ABC | ACB | AB | BC | CB | B ACD | AC | AD | A Cb | b a b. D | b S-derivable = { B } A-derivable = { C, D } B-derivable = C-derivable = D-derivable =

NORMAL FORMS EXAMPLE Given a context-free grammar G with productions S A B C D ABC | ACB | AB | BC | CB | Cb | b ACD | AC | AD | a | b. D | b Cb | b a b. D | b S-derivable = { B } A-derivable = { C, D } B-derivable = C-derivable = D-derivable =

NORMAL FORMS EXAMPLE Given a context-free grammar G with productions S A B C D ABC | ACB | AB | BC | CB | Cb | b ACD | AC | AD | a | b. D | b Cb | b a b. D | b Xb Xbc Xcb Xcd b BC CB CD

NORMAL FORMS EXAMPLE Given a context-free grammar G with productions S A B C D ABC | ACB | AB | BC | CB | CXb | b ACD | AC | AD | a | Xb. D | b CXb | b a Xb. D | b Xb Xbc Xcb Xcd b BC CB CD

NORMAL FORMS EXAMPLE Given a context-free grammar G with productions S A B C D AXbc | AXcb | AB | BC | CB | CXb | b AXcd | CD | AC | AD | a | Xb. D | b CXb | b a Xb. D | b Xb Xbc Xcb Xcd b BC CB CD

NORMAL FORMS THEOREM For any G = ( V, , S, P ) be a context-free grammar, there is a G 1 = ( V 1, , S, P 1 ) be a context-free grammar in CNF so that L(G 1) = L(G) – { }.