ContextFree Grammars CFGs Since sets are Languages grammars

A CFG is composed of the followings components: • Σ, a finite non-empty set

An Example CFG 1. Σ = { a } 1. 2. ΣN == {

S a. Sb | ^ A Notational variation of the same CFG: S a.

CFG: a. Sb | ^ S A Parse Tree for aaabbb based on the

An Example CFG S NP NP D VP N VP V NP D the

According to the CFG given in the previous section, a parse tree for “the

Every Regular Language is a CF Language. Every Regular Grammar(RG) is a CFG. A

Slides: 10

Download presentation

Context-Free Grammars (CFG’s) Since sets are Languages, grammars can be given for defining sets. FORTRAN was defined by Backus and Naur in 1954 in a version of CFG known as the Backus Naur Form (BNF) and then the first compiler was developed for FORTRAN. Every compiler is based on a CFG’s will be introduced with examples in the next few slides. If you do not see anything on the screen then just press Enter a few times.

A CFG is composed of the followings components: • Σ, a finite non-empty set of symbols called Terminals • N, a finite non-empty set of Non-terminals disjoint from Σ; S, is a special start symbol from the set N. 3. P, a set of Productions or grammar rules of the form Ni (Σ + N)* where Ni is a Non-terminal Some books use T for terminals instead of Σ (Often, P, the set of Productions, is explicitly given in a CFG, and implicitly understood) Σ, N are left as

An Example CFG 1. Σ = { a } 1. 2. ΣN == { {a S} } 2. 3. NP == { {S } S a. S 3. P = { S ^ } S a. S S ^ } This CFG generates or derives a* = { ^, a, aaa, aaaaa, . . . } Derivation for the string aa: S => aa Derivation for the string aaa: S => aaa In CFG, the emphasis is on the set of productions, P; therefore, the above CFG can be given as: S a. S S ^ A Notational variation of the same CFG grammar: S a. S | ^

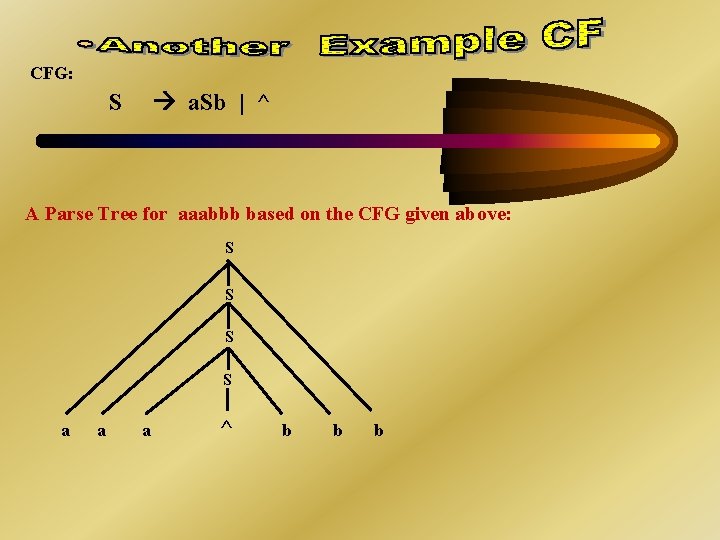
S a. Sb | ^ A Notational variation of the same CFG: S a. Sb S ^ This CFG generates/derives {anbn : where n >= 0} = {^, ab, aabb, aaabbb, aaaabbbb, . . . } (In String Theory, a 0 = ^ , a 0 b 0 = ^^ = ^ ; that is, a 0 != 1 ) Derivation of aaabbb: S => a. Sb => aa. Sbb => aaa. Sbbb => aaabbb The derivation always starts with the start symbol , S , and stops when all Nonterminals are eliminated. => is used in derivation where as is used in grammars.

CFG: a. Sb | ^ S A Parse Tree for aaabbb based on the CFG given above: S S a a a ^ b b b

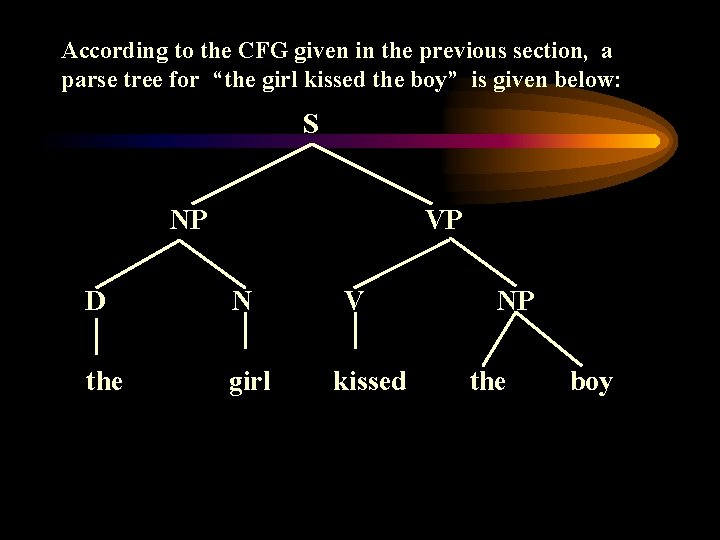
An Example CFG S NP NP D VP N VP V NP D the | a N boy | girl V likes | kissed | saved This CFG can derive: { the boy likes the girl, the girl kissed the boy, a boy saved the girl, . . . } Derivation of the girl kissed the boy: S => NP VP => D N VP => the girl V NP => the girl kissed D N => the girl kissed the boy THE ABOBE DERIVATION IS A LEFT-MOST DERIVATION; because at each step, the LEFT-MOST Non-terminal is expanded.

According to the CFG given in the previous section, a parse tree for “the girl kissed the boy” is given below: S NP VP D N the girl V kissed NP the boy

Every Regular Language is a CF Language. Every Regular Grammar(RG) is a CFG. A Regular Grammar (RG) can be defined as a CFG with the following two types of restrictions on the right hand side of the arrow: (1) Left RG: either a Non-terminal followed by any combination of Terminals, or any combination of Terminals on right side of the arrow. (That is, productions are of the form: Ni NjΣ* | Σ* ) (2) Right RG: any combination of Terminals followed by one Non-terminal, or else any combination of Terminals on right side of the arrow. (That is, productions are of the form: Ni Σ*Nj | Σ* ) The following Right RG (also known as Right Linear Grammar): S a. S | ^ defines L 9 = a* = { ^, a, aaa, aaaaa, . . } The following Left RG (also known as Left Linear Grammar) defines the same language: S Sa | ^