ContextFree Grammars Using grammars in parsers 2301373 Chapter

Context-Free Grammars Using grammars in parsers 2301373 Chapter 3 Context-free Grammar 1

Outline Parsing Process n Grammars n n n Context-free grammar Backus-Naur Form (BNF( Parse Tree and Abstract Syntax Tree n Ambiguous Grammar n Extended Backus-Naur Form (EBNF( n 2301373 Chapter 3 Context-free Grammar 2

Parsing Process Call the scanner to get tokens n Build a parse tree from the stream of tokens n n A parse tree shows the syntactic structure of the source program. Add information about identifiers in the symbol table n Report error, when found, and recover from thee error n 2301373 Chapter 3 Context-free Grammar 3

Grammar n a quintuple (V, T, P, S) where n n V is a finite set of nonterminals, containing S, T is a finite set of terminals, P is a set of production rules in the form of β where and β are strings over V UT , and S is the start symbol. Example G= ({S, A, B, C}, {a, b, c}, P, S( P= { S SABC, BA AB, CB BC, CA AC, SA a, a. A aa, a. B ab, b. B bb, b. C bc, c. C cc{ n 2301373 Chapter 3 Context-free Grammar 4

Context-Free Grammar n a quintuple (V, T, P, S) where V is a finite set of nonterminals, containing S, n T is a finite set of terminals, n P is a set of production rules in the form of β where is in V and β is in (V UT )*, and n S is the start symbol. n n Any string in (V U T)* is called a sentential form. 2301373 Chapter 3 Context-free Grammar 5

Examples E EOE E (E( E id O + O O * O / 2301373 S S SS (S)S () Chapter 3 Context-free Grammar 6

Backus-Naur Form (BNF) n n n Nonterminals are in. < > Terminals are any other symbols. =: : means . |means or. Examples: >E> : : = <E><O><E>| (<E>) | ID >O/ | * | - | + =: : < >S> : : = <S><S> | (<S>)<S> | () | 2301373 Chapter 3 Context-free Grammar 7

Derivation A sequence of replacement of a substring in a sentential form. Definition n Let G = (V, T, P, S ) be a CFG, , , be strings in (V U T)* and A is in V. A G if A is in P. n n *G denotes a derivation in zero step or more. 2301373 Chapter 3 Context-free Grammar 8

Examples S SS | (S)S | () | S SS (S)SS (S)S(())S ((S)())S(())S ((())()) (())S (())(()(())) 2301373 E E O E | (E) | id O /|*|-|+ E EOE (E) O E (E O E) O E *)) E O E) O E ((id O E)) O E) O E ((id + id)) O E * ((id + id)) * id) + id Chapter 3 Context-free Grammar 9

Leftmost Derivation Rightmost Derivation n Each step of the derivation is a replacement of the leftmost nonterminals in a rightmost nonterminals in a sentential form. E EOE (E) O E (E O E) O E (id + id) * E (id + id) * id 2301373 E EOE E O id E * id (E) * id (E O id) * id (E + id) * id (id + id) * id Chapter 3 Context-free Grammar 10

Language Derived from Grammar Let G = (V, T, P, S ) be a CFG. n A string w in T * is derived from G if S * Gw. n A language generated by G, denoted by L(G), is a set of strings derived from G. n n 2301373 L(G) = {w| S * Gw. { Chapter 3 Context-free Grammar 11

Right/Left Recursive n n A grammar is a left recursive if its production rules can generate a derivation of the form A * A X. Examples: n E E O id | (E) | id n E F + id | (E) | id F E * id | id n 2301373 E F + id E * id + id n n A grammar is a right recursive if its production rules can generate a derivation of the form A * X A. Examples: n E id O E | (E) | id n E id + F | (E) | id F id * E | id n E Chapter 3 Context-free Grammar id + F id + id * E 12

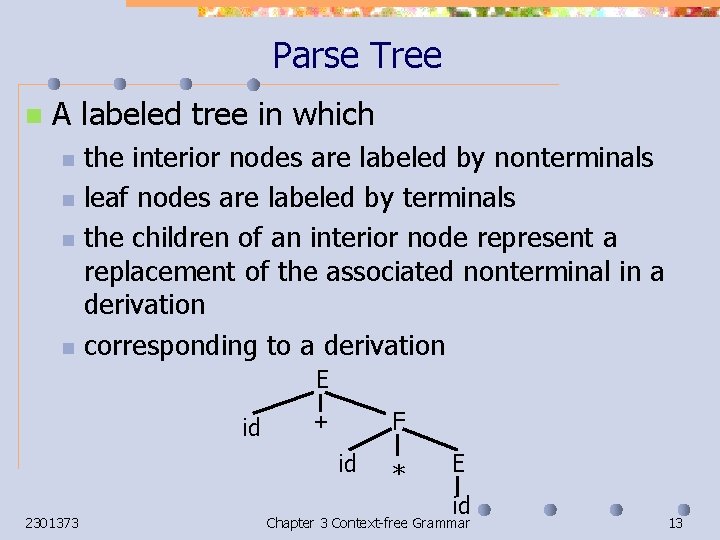
Parse Tree n A labeled tree in which n n the interior nodes are labeled by nonterminals leaf nodes are labeled by terminals the children of an interior node represent a replacement of the associated nonterminal in a derivation corresponding to a derivation E id F + id 2301373 * E id Chapter 3 Context-free Grammar 13

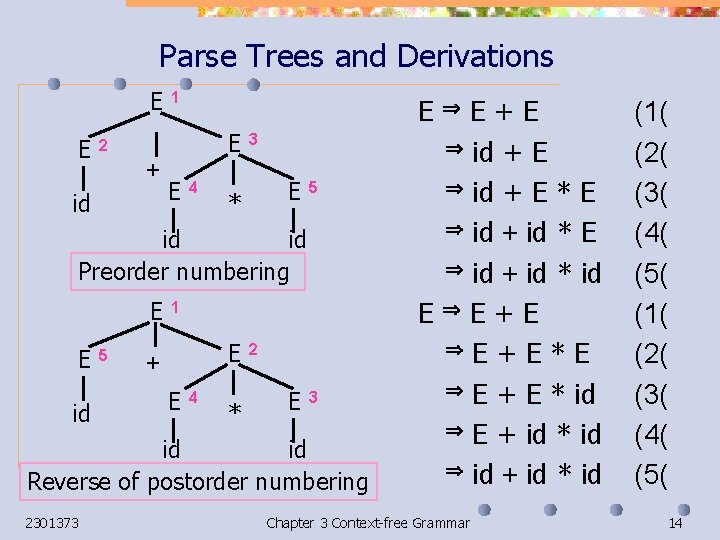
Parse Trees and Derivations E E 1 E E 2 + id E 4 3 E * 5 id id Preorder numbering E E id 5 1 E + E 4 * 2 E 3 id id Reverse of postorder numbering 2301373 E+E id + E * E id + id * id E E+E E + E * id E + id * id Chapter 3 Context-free Grammar (1( (2( (3( (4( (5( 14

Grammar: Example List of parameters in: n Function definition n n function sub(a, b, c) Function call n sub(a, 1, 2) <arg. List> id , <arglist> id, id , <arglist> <arg. List> … (id , )* id <arglist> , id, id … id (, id )* 2301373 <Fdef> function id ( <arg. List> ) <arg. List> id , <arglist> | id <Fcall> id ( <par. List> ) <par. List> <par> , <parlist>| <par> id | const <Fdef> function id ( <arg. List> ) <arg. List> <arglist> , id | id <Fcall> id ( <par. List> ) <par. List> <parlist> , <par>| Chapter 3 Context-free Grammar 15

Grammar: Example List of parameters n If zero parameter is allowed, then ? Work ? NO! Generate id , 2301373 <Fdef> function id ( <arg. List> )| function id ( ) <arg. List> id , <arglist> | id <Fcall> id ( <par. List> ) | id () <par. List> <par> , <parlist>| <par> id | const <Fdef> function id ( <arg. List> ) <arg. List> id , <arglist> | id Chapter 3 Context-free Grammar 16 |

Grammar: Example List of parameters n If zero parameter is allowed, then ? Work ? NO! Generate id , 2301373 <Fdef> function id ( <arg. List> )| function id ( ) <arg. List> id , <arglist> | id <Fcall> id ( <par. List> ) | id () <par. List> <par> , <parlist>| <par> id | const <Fdef> function id ( <arg. List> ) <arg. List> id , <arglist> | id Chapter 3 Context-free Grammar 17 |

Grammar: Example <St> : : = | s; <St> | { <St> } <St> n s; { <St> } { { <St> } <St>} n More than one { { <St> } s; <St>} statement: { { <St> } s; } n s; s; s; { { s; <St> } s; } n A statement can be a { { s; { <St> } s; } block of statements. { { s; { <St> } s; } { { s; { <St> } <St> n {s; s; s; } } s; } Is the following correct? { { s; { <St> } } s; } { {s; s; } s; {}} s; } { { s; { <St> } s; {} } s; } { { s; <St> } s; {} } s; } 2301373 Chapter 3 Context-free Grammar 18 { { s; s; } s; {} } s; } List of statements: n No statement n One statement:

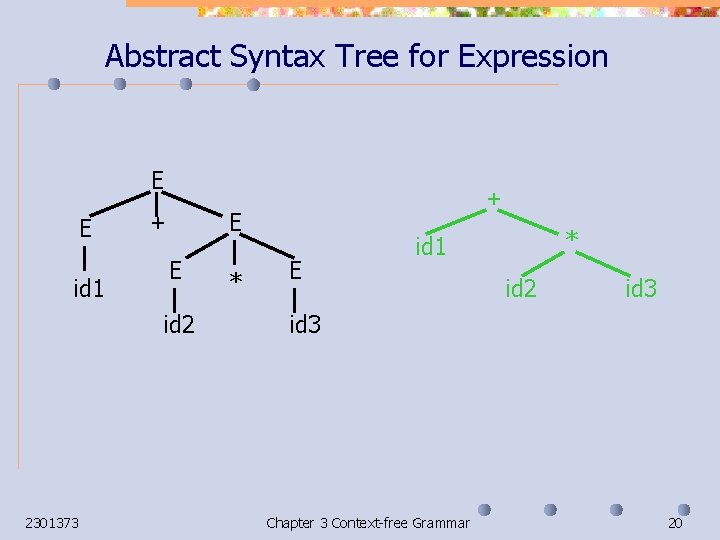
Abstract Syntax Tree Representation of actual source tokens n Interior nodes represent operators. n Leaf nodes represent operands. n 2301373 Chapter 3 Context-free Grammar 19

Abstract Syntax Tree for Expression E E id 1 E + E id 2 2301373 + * E * id 1 id 2 id 3 Chapter 3 Context-free Grammar 20

Abstract Syntax Tree for If Statement st if. Statement if ) exp true ( if st else. Part true else st return 2301373 Chapter 3 Context-free Grammar 21

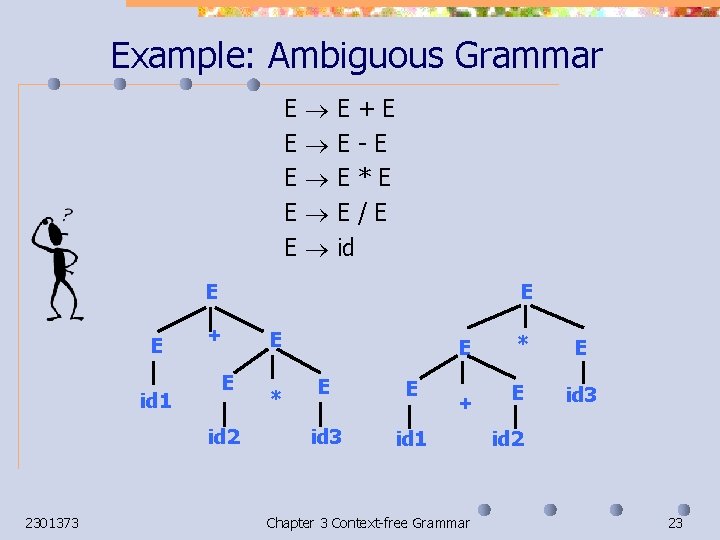
Ambiguous Grammar A grammar is ambiguous if it can generate two different parse trees for one string. n Ambiguous grammars can cause inconsistency in parsing. n 2301373 Chapter 3 Context-free Grammar 22

Example: Ambiguous Grammar E E E E+E E-E E*E E/E id E E id 1 E + E E id 2 2301373 * E E E id 3 id 1 + Chapter 3 Context-free Grammar * E E id 3 id 2 23

Ambiguity in Expressions n Which operation is to be done first? n solved by precedence An operator with higher precedence is done before one with lower precedence. n An operator with higher precedence is placed in a rule (logically) further from the start symbol. n n solved by associativity If an operator is right-associative (or left-associative), an operand in between 2 operators is associated to the operator to the right (left. ( n Right-associated : W + (X + (Y + Z(( n Left-associated : ((W + X) + Y) + Z n 2301373 Chapter 3 Context-free Grammar 24

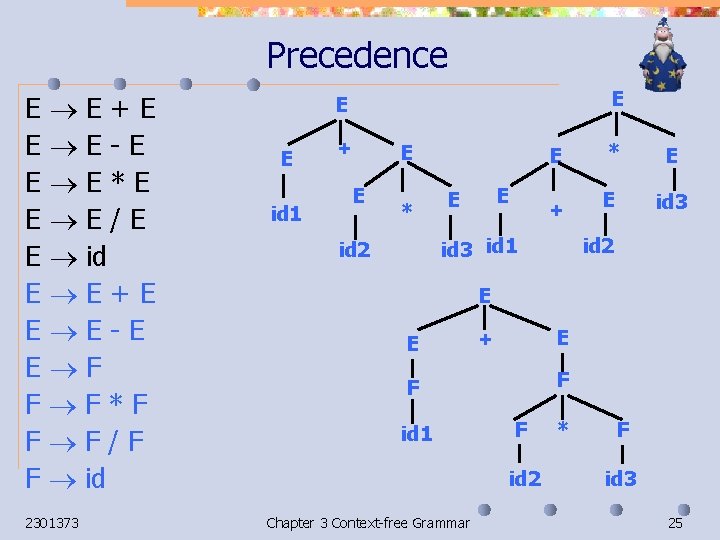
Precedence E E+E E E-E E E*E E E/E E id E E+E E E-E E F F F*F F F/F F id 2301373 E E E id 1 + E E * E E E + id 3 id 1 id 2 * E E id 3 id 2 E E E + F F id 1 F id 2 Chapter 3 Context-free Grammar * F id 3 25

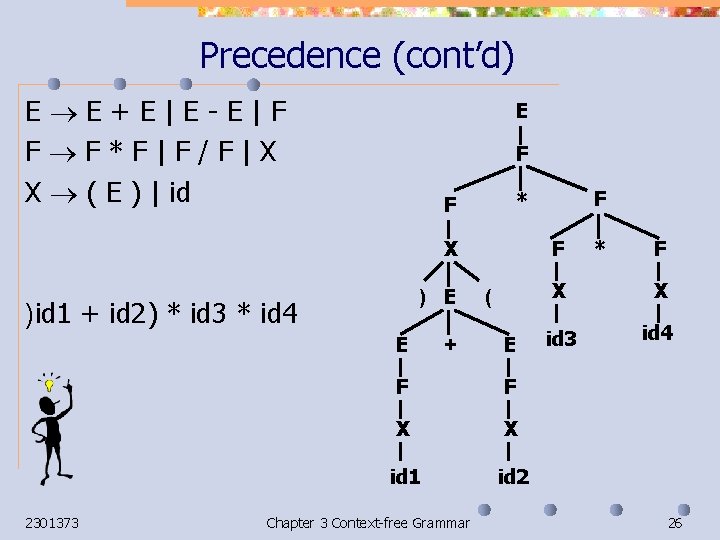
Precedence (cont’d) E E+E|E-E|F F F*F|F/F|X X ( E ) | id E F X ) E )id 1 + id 2) * id 3 * id 4 E 2301373 + F ( E F F X X id 1 id 2 Chapter 3 Context-free Grammar F * F X X id 3 id 4 26

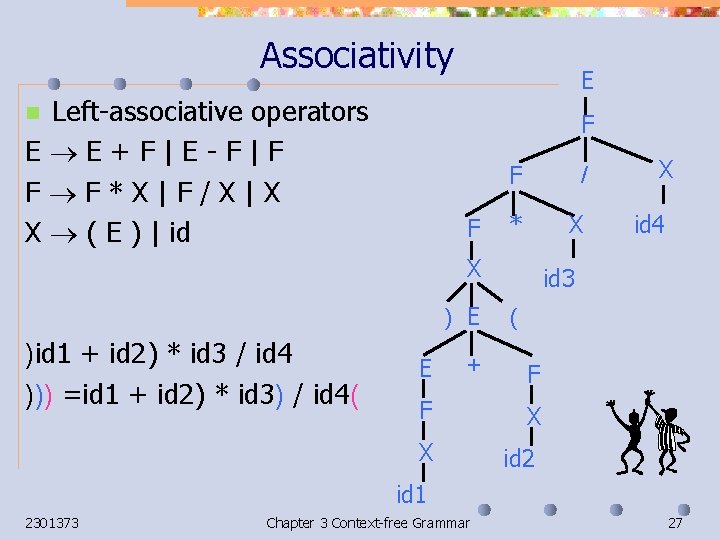
Associativity Left-associative operators E E+F|E-F|F F F*X|F/X|X X ( E ) | id E n F F F / * X X ) E )id 1 + id 2) * id 3 / id 4 ))) =id 1 + id 2) * id 3) / id 4( E + X id 4 id 3 ( F F X X id 2 id 1 2301373 Chapter 3 Context-free Grammar 27

Ambiguity in Dangling Else St If. St. . . | If. St if ( E ) St | if ( E ) St else St E 0 | 1… | If. St if ) }if (0 ( }if (1) St else St{ { E ( If. St if ) St E ( 0 If. St 0 if ) }if (0 ( }if (1) St { else St if else St If. St ) E ( St 1 1 2301373 St Chapter 3 Context-free Grammar 28

Disambiguating Rules for Dangling Else St Matched. St | Unmatched. St if (E) St | St if (E) Matched. St else Unmatched. St Matched. St if (E) Matched. St else Matched. St | Unmatched. St. . . E if ) E ( St 1|0 Matched. St n if (0) if (1) St else St =if (0 ( if ) E ( Matched. St else Matched. St if (1) St else St 2301373 Chapter 3 Context-free Grammar 29

Extended Backus-Naur Form (EBNF) n Kleene’s Star/ Kleene’s Closure n n n Seq : : = St {; St { Seq : : = {St ; } St Optional Part n n 2301373 If. St : : = if ( E ) St [else St[ E : : = F [+ E ] | F [- E[ Chapter 3 Context-free Grammar 30

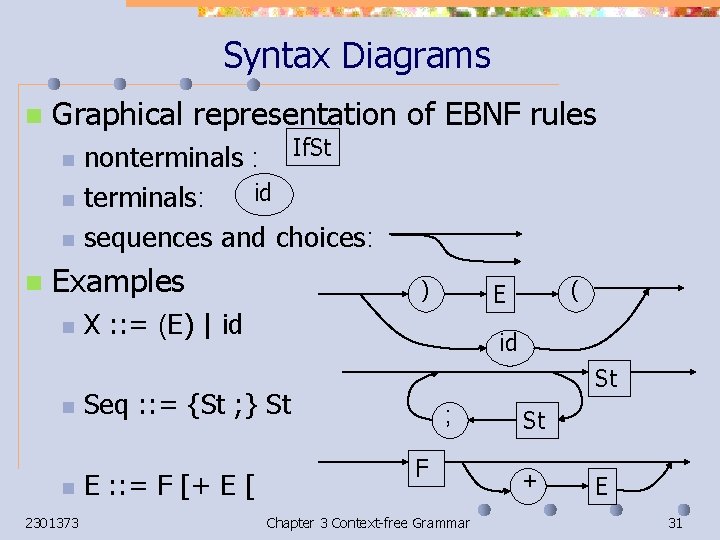
Syntax Diagrams n Graphical representation of EBNF rules n n nonterminals : If. St id terminals: sequences and choices: Examples n n n 2301373 ) X : : = (E) | id id St Seq : : = {St ; } St E : : = F [+ E [ ( E ; F Chapter 3 Context-free Grammar St + E 31

Reading Assignment n Louden, Compiler construction n 2301373 Chapter 3 Context-free Grammar 32