The Chomsky Hierarchy 1 Unrestricted Grammars Productions String

The Chomsky Hierarchy 1

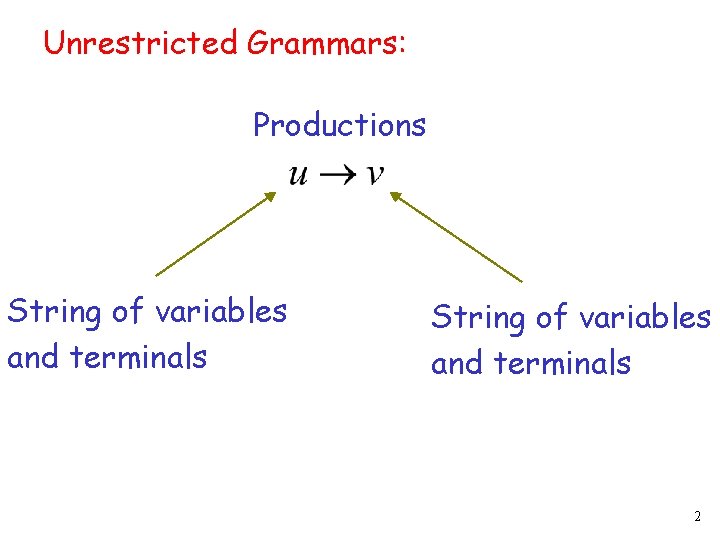
Unrestricted Grammars: Productions String of variables and terminals 2

Example unrestricted grammar: 3

Theorem: A language is recursively enumerable if and only if is generated by an unrestricted grammar 4

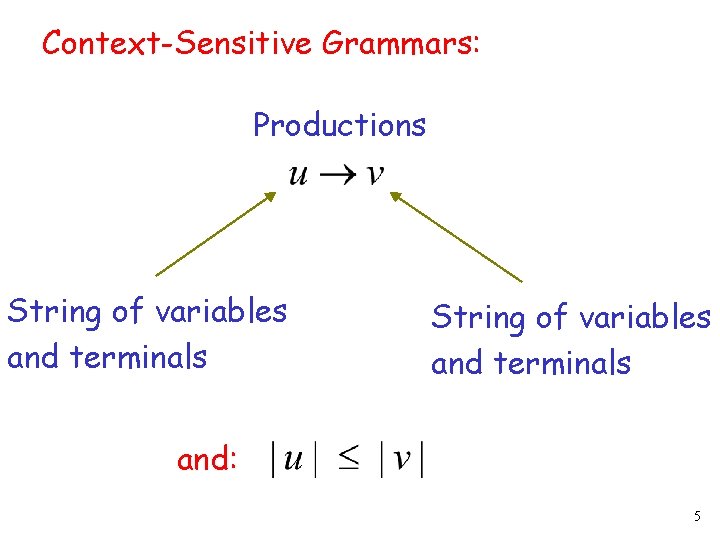
Context-Sensitive Grammars: Productions String of variables and terminals and: 5

The language is context-sensitive: 6

Theorem: A language is context sensistive if and only if is accepted by a Linear-Bounded automaton 7

Observation: There is a language which is context-sensitive but not recursive 8

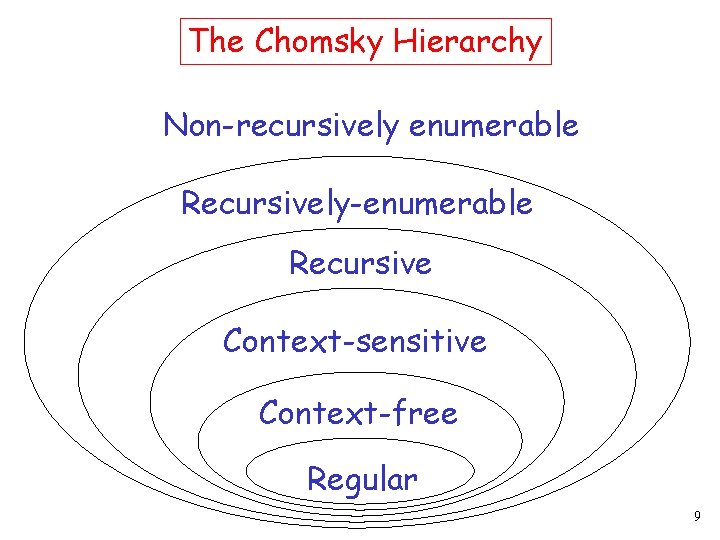
The Chomsky Hierarchy Non-recursively enumerable Recursively-enumerable Recursive Context-sensitive Context-free Regular 9

Decidability 10

Consider problems with answer YES or NO Examples: • Does Machine • Is string • Does DFA have three states ? a binary number? accept any input? 11

A problem is decidable if some Turing machine Solves (decides) the problem Decidable problems: • Does Machine • Is string • Does DFA have three states ? a binary number? accept any input? 12

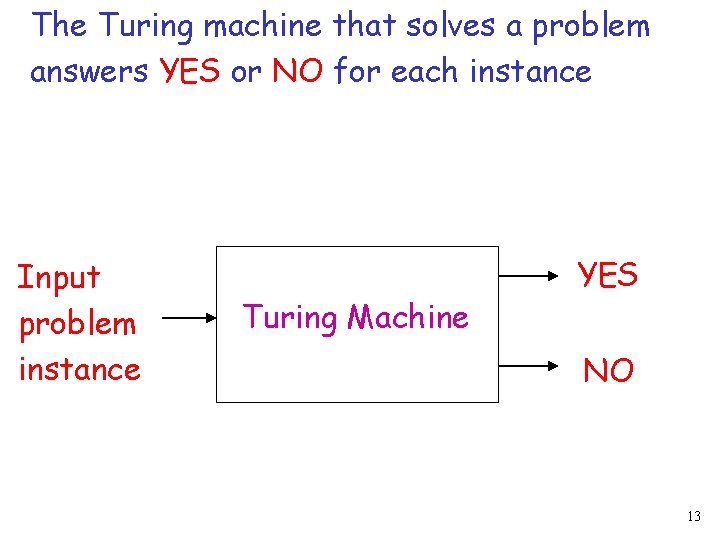
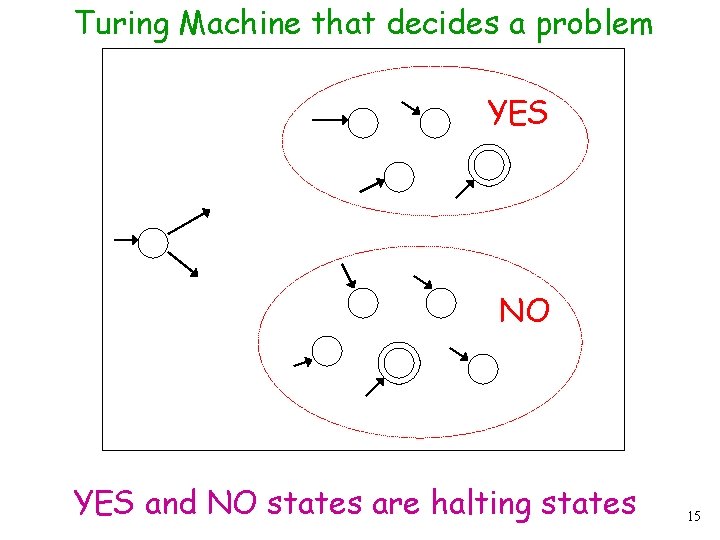
The Turing machine that solves a problem answers YES or NO for each instance Input problem instance Turing Machine YES NO 13

The machine that decides a problem: • If the answer is YES then halts in a yes state • If the answer is NO then halts in a no state These states may not be final states 14

Turing Machine that decides a problem YES NO YES and NO states are halting states 15

Difference between Recursive Languages and Decidable problems For decidable problems: The YES states may not be final states 16

Some problems are undecidable: There is no Turing Machine that solves all instances of the problem 17

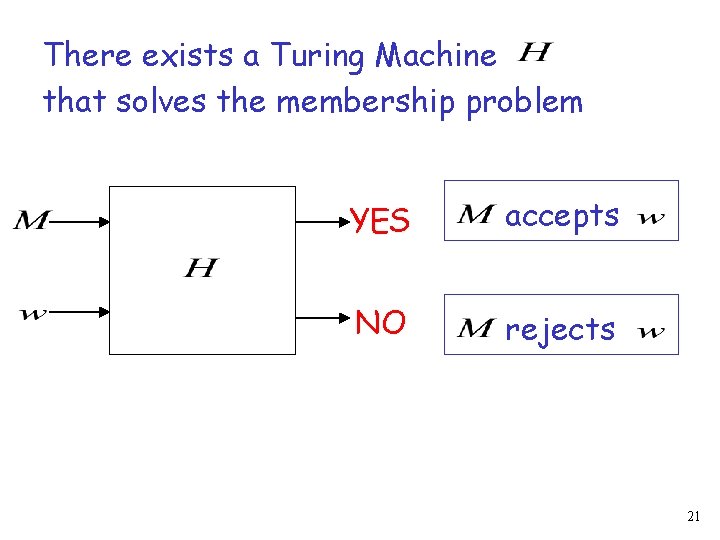
A simple undecidable problem: The membership problem 18

The Membership Problem Input: • Turing Machine • String Question: Does accept ? 19

Theorem: The membership problem is undecidable Proof: Assume for contradiction that the membership problem is decidable 20

There exists a Turing Machine that solves the membership problem YES accepts NO rejects 21

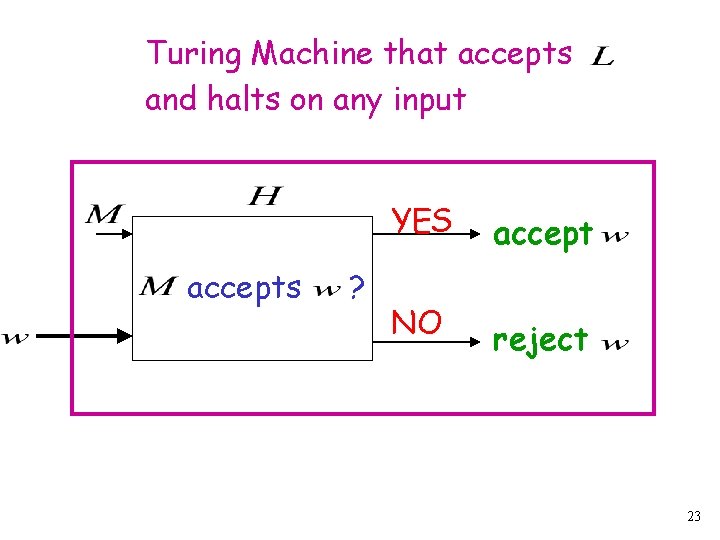
Let be a recursively enumerable language Let be the Turing Machine that accepts We will prove that is also recursive: we will describe a Turing machine that accepts and halts on any input 22

Turing Machine that accepts and halts on any input accepts ? YES accept NO reject 23

Therefore, is recursive Since is chosen arbitrarily, we have proven that every recursively enumerable language is also recursive But there are recursively enumerable languages which are not recursive Contradiction!!!! 24

Therefore, the membership problem is undecidable END OF PROOF 25

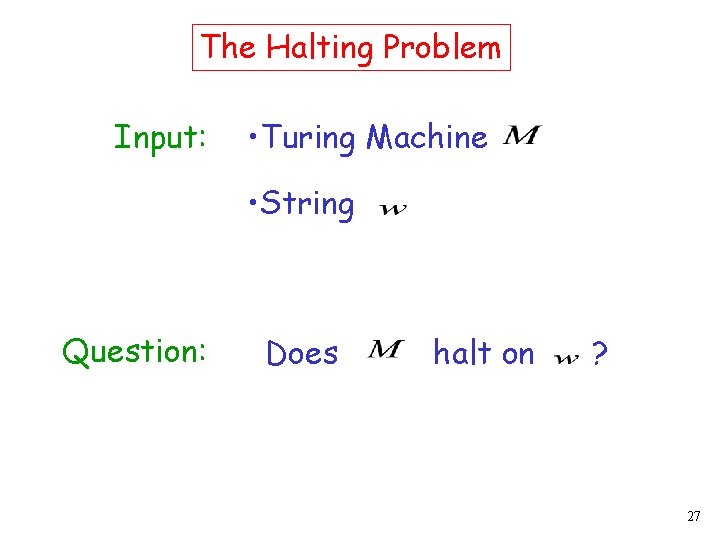
A famous undecidable problem: The halting problem 26

The Halting Problem Input: • Turing Machine • String Question: Does halt on ? 27

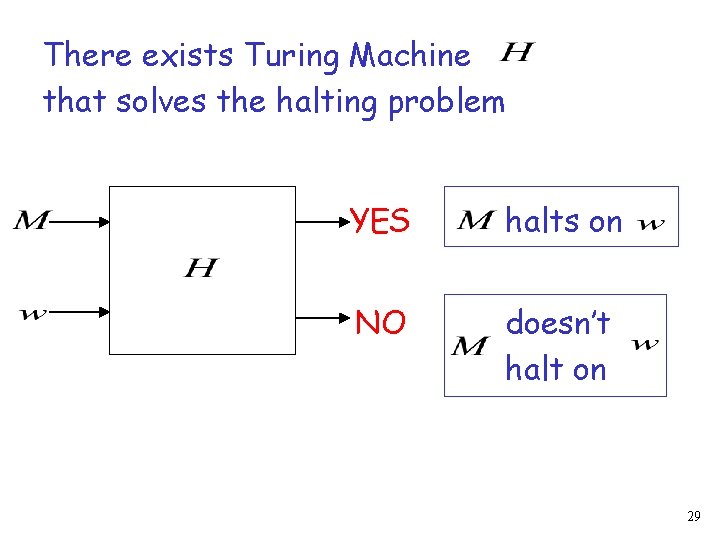
Theorem: The halting problem is undecidable Proof: Assume for contradiction that the halting problem is decidable 28

There exists Turing Machine that solves the halting problem YES halts on NO doesn’t halt on 29

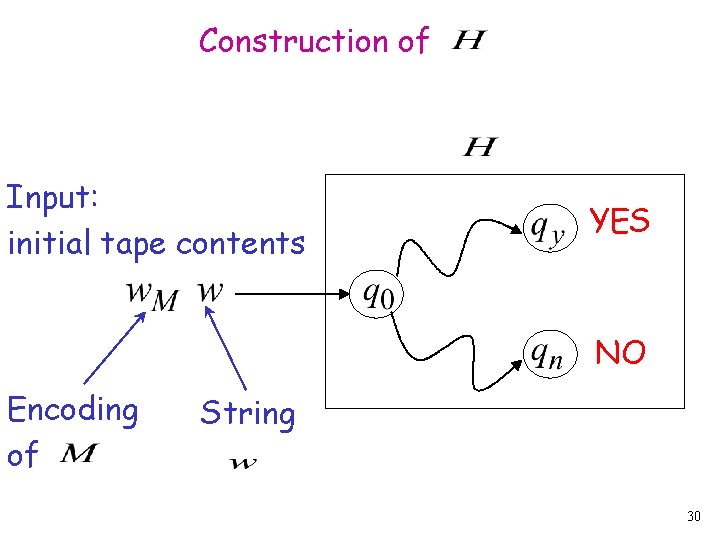
Construction of Input: initial tape contents YES NO Encoding of String 30

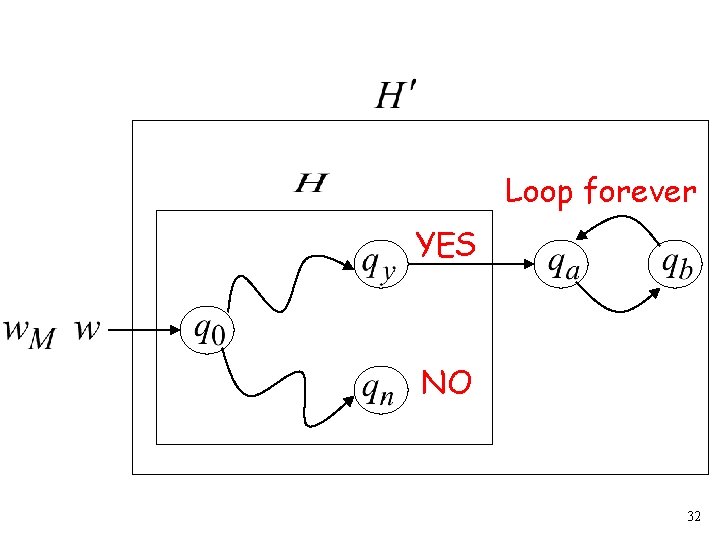
Construct machine : If returns YES then loop forever If returns NO then halt 31

Loop forever YES NO 32

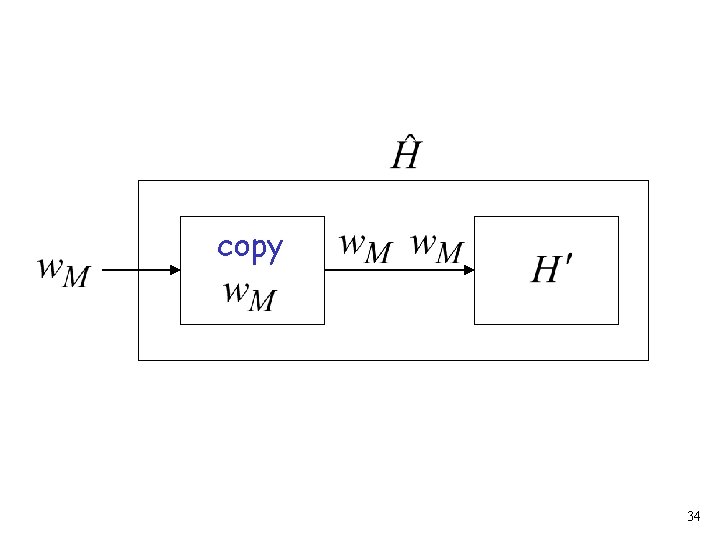
Construct machine Input: If : (machine ) halts on input Then loop forever Else halt 33

copy 34

Run machine Input: If with input itself: (machine ) halts on input Then loop forever Else halt 35

on input : If halts then loops forever If doesn’t halt then it halts NONSENSE !!!!! 36

Therefore, we have contradiction The halting problem is undecidable END OF PROOF 37

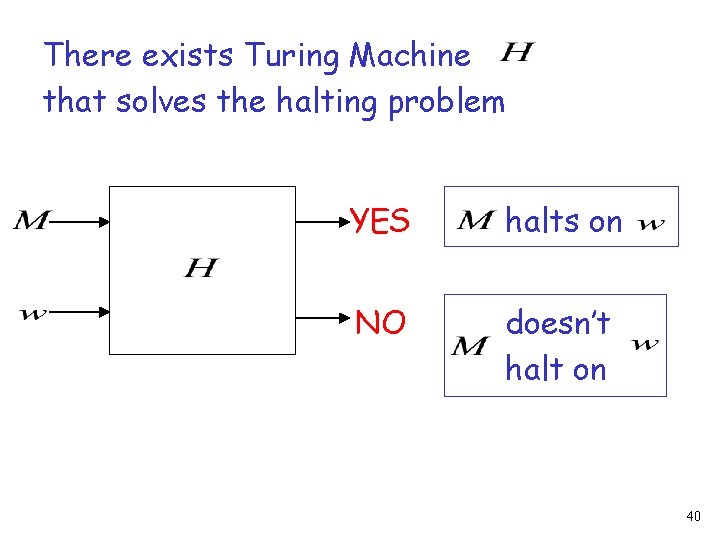
Another proof of the same theorem: If the halting problem was decidable then every recursively enumerable language would be recursive 38

Theorem: The halting problem is undecidable Proof: Assume for contradiction that the halting problem is decidable 39

There exists Turing Machine that solves the halting problem YES halts on NO doesn’t halt on 40

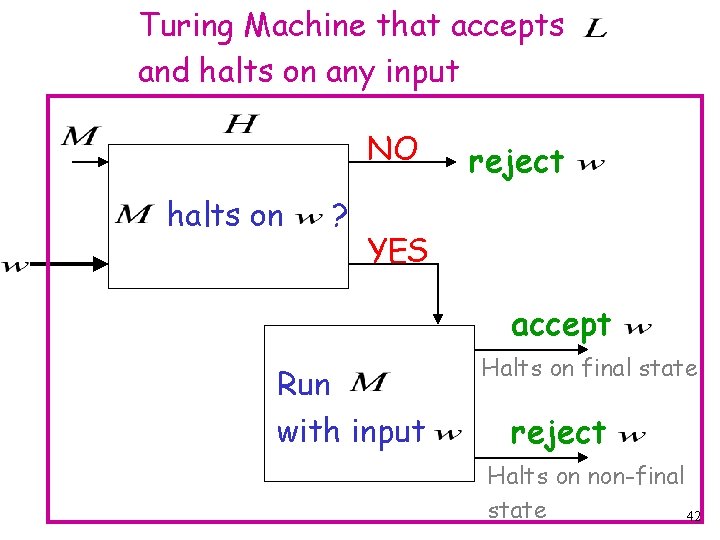
Let be a recursively enumerable language Let be the Turing Machine that accepts We will prove that is also recursive: we will describe a Turing machine that accepts and halts on any input 41

Turing Machine that accepts and halts on any input NO halts on ? reject YES accept Run with input Halts on final state reject Halts on non-final state 42

Therefore is recursive Since is chosen arbitrarily, we have proven that every recursively enumerable language is also recursive But there are recursively enumerable languages which are not recursive Contradiction!!!! 43

Therefore, the halting problem is undecidable END OF PROOF 44